Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 4 Analytical Electron Microscopy 365

procedures (Schaffer et al., 2004), these datasets have the advantage

that the background extrapolation can be carried out with much higher

precision than in the three-window technique. Energy windows as

small as 0.1 eV have been used on instruments equipped with mono-

chromators and high-resolution ﬁ lters corrected up to third-order

aberrations (Hofer et al., 2005). Quantitative analysis to extract the

absolute atomic density and deconvolution of the effects of multiple

scattering are also possible since the full spectrum is retrievable at

each pixel (Thomas and Midgley, 2001b). In fact, for each pixel of the

image sequence the intensity can be measured and a spectrum of

energy resolution equivalent to the width of the energy-selecting

slit is deduced. Based on limited sequences of images with narrow

energy windows (1–2 eV) and selection of spectra at the edge threshold,

this approach has demonstrated that changes in the near-edge struc-

ture due to variations in the chemical bonding state of elements are

visible (Muller et al., 1993; Botton and Phaneuf, 1999; Bayle-Guillemaud

et al., 2003; Hofer et al., 2000). This capability suggests that similar to

X-ray absorption scanning transmission microspectroscopy (e.g., Hitch-

cock et al., 2005), bonding changes can be visualized with EELS

mapping, albeit with a spatial resolution typical of EFTEM images (see

Section 6.2.3).

6.2.2 STEM-EELS Mapping

The other variant of the more advanced EELS imaging technique

makes use of developments in fast detectors, large storage capacity, and

fast computers. The approach is based on the use of STEM instruments

equipped with parallel or dedicated 2D fast detectors. The original idea

of this technique was proposed by the Orsay group (Jeanguillaume

and Colliex, 1989) and implemented in subsequent years by various

groups (Hunt and Williams, 1991; Botton and L’Espérance, 1994; Colliex

et al., 1994). As for EFTEM spectrum imaging, the STEM-EELS imaging

is also commercially available from the spectrometer manufacturer

Gatan. The technique involves the sequential acquisition of an energy

loss spectrum (acquired with the photodiode array or a 2D detector)

at each pixel of a rastered area. The ﬁ lling of the data cube (Figure 4–79)

is thus achieved by scanning the beam over each pixel of the area of

interest (pixel by pixel in two dimensions or over a line across inter-

faces) with the third (and fourth) dimension in the data cube being the

energy loss spectrum (energy and intensity).

The advantage of this approach is the availability of the full spec-

trum at each pixel making it easy to implement various data-mining

approaches. Signals can be extracted with advanced methods, includ-

ing multiple least-squares techniques, and the detailed shapes of the

near-edge structures can be ﬁ tted with reference standards from dif-

ferent phases. This technique can therefore be used to map changes in

the chemical bonding environment of atoms in nanoscale structures

as in EFTEM imaging but with much higher spectral sampling. Through

the analysis of a single edge and with reference standards, it is thus

possible to extract the distribution of the individual phases rather than

just the chemical composition. This powerful technique can be imple-

366 G. Botton

mented in one or two dimensions (Figure 4–80) for core loss near-edge

structure features and also for low-loss features. Using the differences

in low-loss spectra of various biological structures and ice, Sun et al.

(1995) were able to map the distribution of the various functional com-

ponents in cells (Figure 4–81). Similarly, for the analysis of polymer-

based materials, the use of low-loss features related to the presence of

π and π + σ plasmons has been used to distinguish polystyrene and

polyethylene in composite blends (Figure 4–82) (Oikawa, 2006; Hunt

et al., 1995).

6.2.3 Quantitative EELS Imaging

If core-loss spectra are combined with low-loss spectra acquired from

the same pixel, it is possible to retrieve more quantitative information

on the sample. Hence, deconvolution techniques (Section 8.2) can be

applied to retrieve the single scattering distribution for accurate quan-

tiﬁ cation (Section 4.2), dielectric function measurements (Section 8.2),

Figure 4–79. Schematic description of the STEM spectrum imaging technique

(STEM-SI). For each pixel of the rastered area an energy loss spectrum is

acquired. Although the spatial sampling is typically lower than in the EFTEM-

SI technique, the spectral sampling is higher with easy recording of the

near-edge structure features at each pixel.

Chapter 4 Analytical Electron Microscopy 367

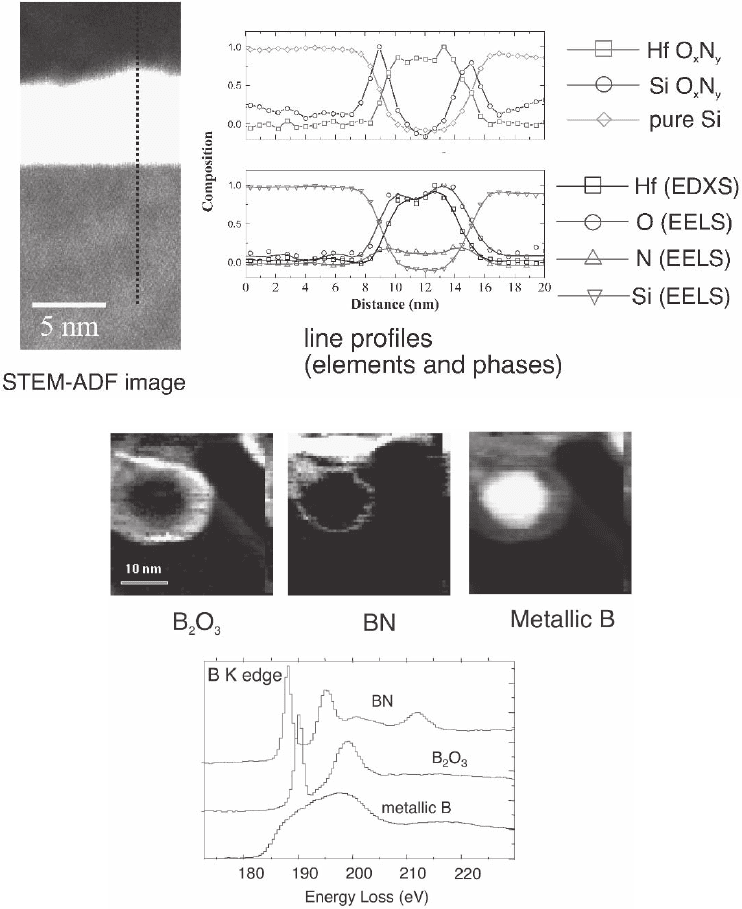
Figure 4–80. (a) Application of the STEM-SI technique to determine the distribution of elements

across interfaces between a high dielectric constant material (Hf-O-N) and Si (STEM annular dark-ﬁ eld

image, left). EDXS spectra and EELS spectra were recorded simultaneously to extract the elemental

composition (bottom right proﬁ le). By analysis of the near-edge structure shape of the Si L

edge and

O K edge, it is possible to distinguish and map the contribution of pure Si, Si-O-N, and Hf-O-N.

(Courtesy of M. Couillard, McMaster University.) (b) Two-dimensional phase maps of B nanostructure

with BN, B

, and metallic B separated according to the shape of the near-edge structure spectra of

the B K edges using the STEM-Spectrum imaging technique and least-squares ﬁ tting of spectra. The

structure consists of a metallic B core with a thin BN shell and outer thick shell of B

. (Courtesy of

O. Stephan and C. Colliex, University Paris-Sud.)

368 G. Botton

Figure 4–81. STEM images and phase component maps in frozen hydrated liver tissue. (a) Low-dose

dark-ﬁ eld STEM image sectioned sample showing no contrast; (b) bright-ﬁ eld image of the same region

based on integration of all signals on the spectrum at each pixel of the STEM-SI (the intensity drop is

due to the variation of beam current during the acquisition); (c) relative thickness map (t/λ), contrast

is visible on the lipid droplets; (d) water maps and identiﬁ cation of the various biological components

based on the multiple least-squares ﬁ t of the low-loss spectra with water and protein reference com-

pounds and the amount of water within the structure: L, lipid droplet (zero water content); P, plasma

(91% water); R, erythrocyte (65% water); M, mitochondria (57% water); (e) low-energy loss spectra of

reprinted with permission from Blackwell Publishing.)

Chapter 4 Analytical Electron Microscopy 369

and the thickness relative to the inelastic mean free path of the sample

(Section 8.2), and also to implement quantitative statistical analysis

(Bonnet et al., 1999) to retrieve signiﬁ cant spectral components and

analyze changes in bonding at interfaces in materials. Thickness maps,

relative to the mean free path (Section 8.2), can be obtained with the

EFTEM and STEM imaging approaches by acquiring a zero-loss image

(x,y) and an unﬁ ltered image I

(x,y). Following the approach dis-

cussed in Section 8.2 for the analysis of individual spectra to obtain

relative thickness (t/λ) values, the ratio of the two images can be com-

bined to give the relative thickness map I

t/λ

(x,y) = ln[I

(x,y)/I

(x,y)]. The

variant of this EFTEM method is to acquire the low-loss spectrum at

each pixel and process the individual spectra to deduce t/λ at each

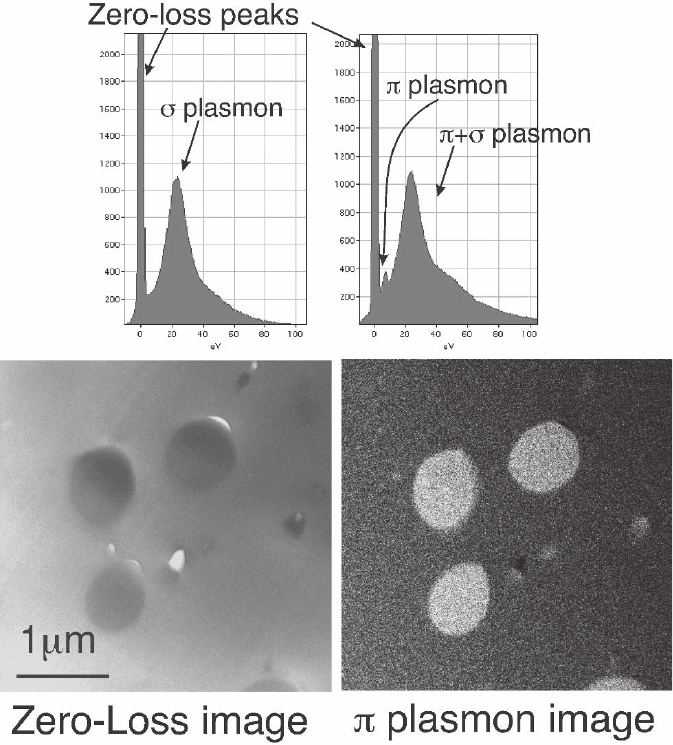
Figure 4–82. Section of polyﬁ n–polycarbonate polymer composite. The low-loss spectrum of the

polyﬁ n (top left) does not show the π plasmon resonance visible on the spectrum of the polycarbonate

material (top right). The zero-loss image (bottom left) does not show strong contrast between the two

phases while the π plasmon energy-ﬁ ltered image (bottom right) clearly makes it possible to distin-

guish the regions where the polycarbonate is present. (Courtesy of Dr. T. Oikawa, JEOL.)

370 G. Botton

point of an image (see Section 8.2). This information on the sample

thickness is valuable for the determination of the volume of the sample

under analysis (hence the volume fraction of particular phases or

defects), or to determine whether the changes in thickness affect the

apparent intensity of elemental maps. The thickness information is also

useful to verify whether the thickness of the sample is beyond the

critical thickness at which accurate extraction and quantiﬁ cation can

be carried out (Section 4.2.4). Finally, the thickness information, if

combined with EDXS maps, can lead to fully quantitative X-ray maps

accounting for X-ray and absorption corrections.

As in the case of EDXS imaging, elemental maps can also be com-

bined to retrieve fully quantitative concentration maps and deduce

phase analysis histograms using experimental k-factors or cross sec-

tions (Hofer et al., 1997; Kothleitner and Hofer, 2003). The advantage

of concentration maps is, as in the case of EDXS mapping, the fact that

within a range of relative thickness t/λ < 0.5, images are independent

of thickness as discussed in Section 4.2.4. Diffraction effects due to

elastic scattering of electrons outside the objective aperture can also

lead to apparent variations in the intensity of elemental maps and can

be canceled out using the jump-ratio imaging technique. Concentration

maps based on the single scattering distribution of energy losses

obtained after deconvolution of the full spectrum at each pixel show

that reliable quantitative images can be obtained for thickness up to

t/λ ≅ 2 (Thomas and Midgley, 2001a).

Another useful technique demonstrating the removal of diffraction

effects is the use of the rocking beam method during the acquisition

of energy-ﬁ ltered images. In this approach, the incident electron beam

is tilted over a cone of angles (of the order of the Bragg angle) so as to

average out the local diffraction effects including deviations of the

scattering due to dislocations. Energy-ﬁ ltered images with little dif-

fraction contrast can thus be obtained even in bent and highly deformed

samples (Hofer and Warbichler, 1996; Hofer et al., 2000) (Figure 4–83).

Removal of diffraction contrast for qualitative imaging and visualiza-

tion of precipitates in highly deformed samples has also been demon-

strated using ratios of plasmon images obtained at different energies

(Carpenter, 2004).

Various aspects of optimization of signals for EFTEM and STEM-

EELS maps, including the position of energy windows, automatic

detection of edges, illumination conditions, and magniﬁ cation, are dis-

cussed in the work of Kothleitner and Hofer (1998, 2003), Grogger

et al. (2003), Berger and Kohl (1992, 1993), and Berger et al. (1994).

Through image analysis of the quantitative maps, it is also possible to

segment images based on the composition and relative fraction of ele-

ments (Hofer et al., 1997, 2000). Algorithms to allow automatic detec-

tion of edges, for quantitative analysis of phase distributions, for the

determination of thresholds for phase detection and problematic zones

in the samples have also been developed with the use of full spectra

recorded in STEM mode (Kothleitner and Hofer, 2003). Corrections of

drifts in EFTEM images for quantitative analysis have been discussed

in detail in Schaffer et al. (2004).

Chapter 4 Analytical Electron Microscopy 371

6.2.4 Spatial Resolution in EFTEM Elemental Mapping

The resolution in EFTEM elemental mapping depends on several

factors related to the operation parameters of the microscope and the

energy loss of interest so that further discussion of this topic is required.

When no angular limiting aperture is present (in imaging the objective

aperture would be limiting the scattering angles) the dominant factor

is related to the chromatic aberration term discussed in Section 5.2. For

general conditions, however, we must summarize the contributions

that need to be added in quadrature to retrieve the total broadening of

an object point (Krivanek et al., 1995b).

1. Following the discussion in Section 5.2, the chromatic aberration

broadening term when a limiting aperture is used can be described

∆

(68)

where β is the collection angle (limited by the objective aperture in

imaging mode), ∆E is the width of the energy window used to acquire

the image, and E

is the incident energy. This expression assumes that

images are focused at the energy loss E where the energy window is

located (rather than at the elastic image) and that the aperture is ﬁ lled

with the electrons. This assumption is important since, as discussed in

Section 5.2, the width of angular distribution of scattering can be

smaller and the contribution to the chromatic aberration term would

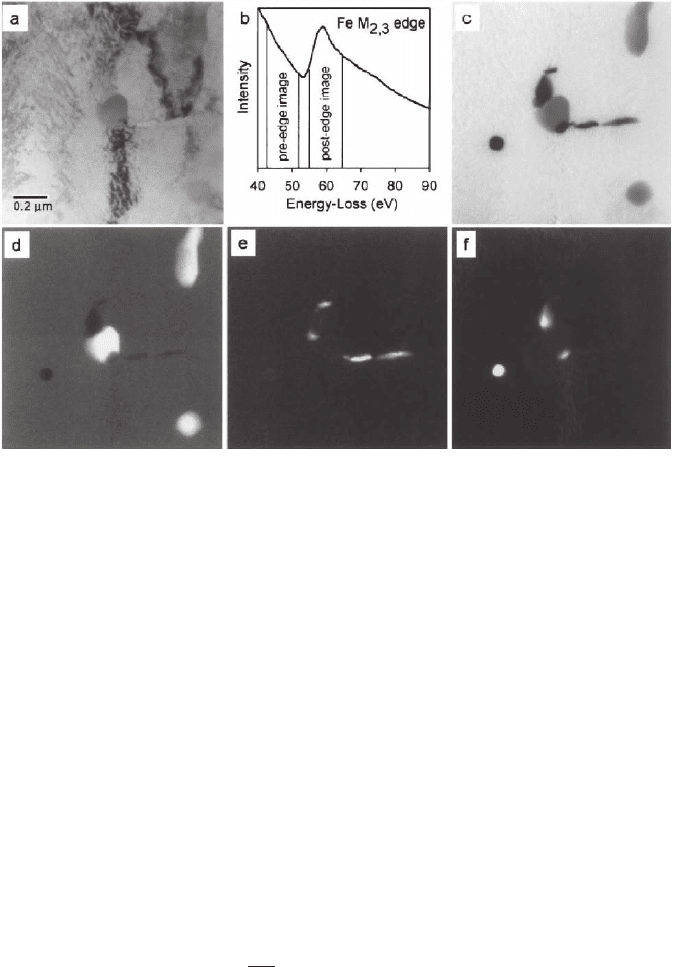
Figure 4–83. Imaging of precipitates in a steel sample. (a) TEM bright-ﬁ eld image of the 10% Cr

steel with Cr

-VN and Nb(C,N) precipitates. (b) EELS spectrum with the Fe-M

edge. (c) Fe-M

jump-ratio image recorded with the rocking beam illumination. (d) Cr-L

jump-ratio image. (e) V-L

jump-ratio image. (f) Nb-M

Springer Science+Business Media.)

372 G. Botton

be modiﬁ ed. As experimental conditions often impose some conver-

gence in the illumination and the chromatic aberration term is small

compared to the subsequent broadening terms for low scattering angles

(either limited by β or θ

) this assumption if often assumed to be

valid.

2. The delocalization of inelastic scattering term b [introduced

in Section 5.2, Eq. (64)] contributes to the broadening with an energy

and angular-dependent term increasing at low energy losses and

low scattering angles (large scattering angles imply a small impact

parameter).

3. The diffraction limit contribution arises from use of the objective

aperture and dominates for small angles due to the denominator

term

= 0.6 λ/β (69)

4. The spherical aberration term d

= 2C

strongly varies with β

and is considered to contribute to a uniform background in the image

and a decrease of contrast when the conditions are optimized for

minimal chromatic aberration contributions (Krivanek et al., 1995b).

Egerton’s work (1999) showed that this term is smaller than the chro-

matic aberration term for typical energy windows used for EFTEM

mapping, but for small energy windows (a few electronvolts wide as

used, for example, in EFTEM spectrum imaging) the term will domi-

nate the resolution at high collection angles and will need to be included

in the analysis. Experimental evidence suggests that the term should

be neglected given the good spatial resolution of energy-ﬁ ltered images

with relatively large collection angles.

Additional terms affecting the resolution depend on the noise in the

images (requiring averaging of signals and increase of acquisition

time), radiation damage of the specimen due to the high doses required

for imaging at core losses, and instabilities of the sample and micro-

scope leading to drift of the area under analysis during acquisition.

Considering the signiﬁ cant terms added in quadrature it is possible

to determine the ultimate physical limits to EFTEM mapping resolu-

tion (Krivanek et al., 1995b)

tot

= d

+ (2b)

+ d

(70)

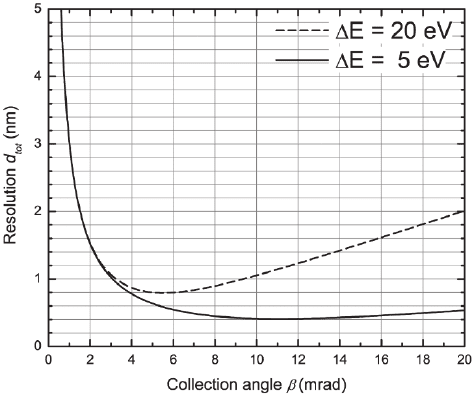
The trends, as a function of collection aperture, suggest that there

are optimal operating conditions for a given energy loss, energy

window ∆E, and microscope characteristics (Figure 4–84). When energy

losses of the order of a few hundred electronvolts are analyzed, for

small collection angles the diffraction limit term dominates, while

for large angles the chromatic aberration term is most important. The

width of the energy window has a signiﬁ cant effect on the resolution

as it is linearly related to the chromatic contribution. Quite often,

large energy windows are used to increase the counting statistics and

reduce the noise in the images. When the energy window is large, the

choice of the optimal collection aperture is more crucial as the chro-

matic aberration term rises steeply. For modern analytical TEMs oper-

Chapter 4 Analytical Electron Microscopy 373

ating at or above 200 keV, and for lenses with chromatic aberration

parameters around 1 mm, the delocalization term [Eq. (64)] is not a

limiting factor for core losses above around 500 eV. For lower energy

losses, in the order of 100 eV or less, this term can dominate the resolu-

tion limit in theory. Experimental results in the literature, however,

suggest that the low losses delocalization terms based on Eq. (64) are

overestimated (Muller and Silcox, 1995; Grogger et al., 2005). For high

core losses, elemental maps show resolution limits consistent with the

calculations of optimal values given above (e.g., below 1 nm based on

Figure 4–84) while for low energy losses (including plasmon losses

around 10–20 eV), images with a resolution around 1 nm (signiﬁ cantly

better than the prediction of 4–5 nm) have been obtained (Grogger

et al., 2005).

Based on the signiﬁ cant contributions of chromatic aberrations for

EFTEM imaging, the optimal approach to achieve the ultimate spatial

resolution limits in EELS mapping, as imposed by unavoidable delo-

calization, is to use the STEM approach with small and high-intensity

probes achievable today on modern analytical electron microscopes.

With current technology making use of bright electron sources and

aberration correctors it is possible to focus several hundred picoam-

peres of current into a near 2 Å probe [Sections 2.1 and 2.2 and Chapter

2 (this volume)].

Examples of chemical analysis with a noncorrected STEM demon-

strate the ability to resolve individual atomic planes of Ca in the

8+δ

superconductor (Figure 4–85) and analyze half-unit

cell defects where the Ca planes are not present, suggesting the exis-

tence of a Bi

8+δ

subunit cell intergrowth.

Figure 4–84. Calculations of the expected resolution in EFTEM elemental

maps at the oxygen K edge (530 eV) as a function of the collection angle for

two energy-ﬁ ltering windows of width ∆E = 5 and 20 eV and C

= C

= 1 mm

(at 200 keV).

374 G. Botton

7 Detection Limits in Microanalysis

The very high spatial resolution of both EDXS and EELS results in rela-

tively low detection limits for most elements as compared to “bulk”

analysis methods. This effect is caused by a combination of factors

including the small analyzed volumes, the low signals resulting from

poor efﬁ ciency in signal collection, or/and low incident beam current,

high background, short acquisition time, and instrumental contribu-

tions. Two quantities characterize the detection limits for EDXS and

EELS depending on information of interest. The minimum detectable

fraction (MDF) refers to a dilute element uniformly distributed in the

Figure 4–85. High-resolution EELS proﬁ le of Ca in Bi

8-δ

based on

the Ca L

edge showing the detection of a single plane of Ca in the half-unit

cell of the structure. The central panel shows a high-angle annular dark-ﬁ eld

image of the sample. The proﬁ le shows the presence of a half-unit cell defect

of the Bi

8-δ

phase (where there is a missing plane of Ca) in the

structure. (Courtesy of Y. Zhu, McMaster University.)