Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 4 Analytical Electron Microscopy 385

8.1 Energy Loss Near Edge Structure

As discussed in the introductory section of this chapter, ELNES provide

information on the electronic structure and bonding environment of the

atoms probed by the incident fast electrons. An example of the informa-

tion is demonstrated in Figure 4–93 showing the relationship between

Figure 4–93. Relationship between the near-edge structure observed on the

EELS edges and the unoccupied electronic states. (a) Transitions are observed

from core levels to unoccupied electronic states above the Fermi level. (b)

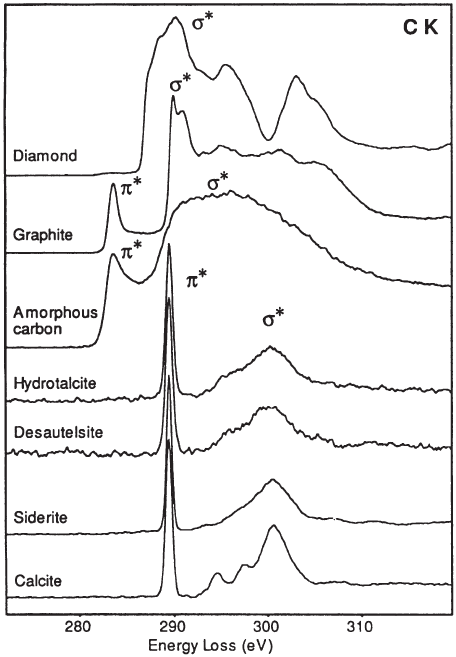
Example of near-edge structure (experimental spectrum) for the C K edge in

graphite with the relationship between the π and σ orbitals (and the antibond-

ing orbitals π* and σ*) in the hybridized atoms and the related bands in the

solid.

386 G. Botton

the spectrum and the energy states along with examples of near edge

structures for different compounds (Figure 4–94). The features visible

in the near edge structure represent the unoccupied energy states as

modiﬁ ed with respect to a free atom by effects such as hybridization,

coordination changes, and solid-state effects. The technique therefore

provides data equivalent to the well-established X-ray absorption near-

edge structure (XANES) spectroscopy carried out in synchrotrons. As

such, reference data and literature from XANES can often be used to

identify compounds and understand trends and electronic structure

effects in ELNES. Examples of changes in the ELNES derived from

changes in the electronic structure demonstrate the sensitivity to the

structural environment and the chemical state (Figure 4–94). In addition

to the changes in the shape of near edge structures, the energy position

of the edges can vary with the oxidation state in a manner similar to X-

ray photoelectron spectroscopy. Changes in the core energy level and

the position of unoccupied states can result from charge transfer effects

due to oxidation, bonding, and coordination changes. Systematic trends

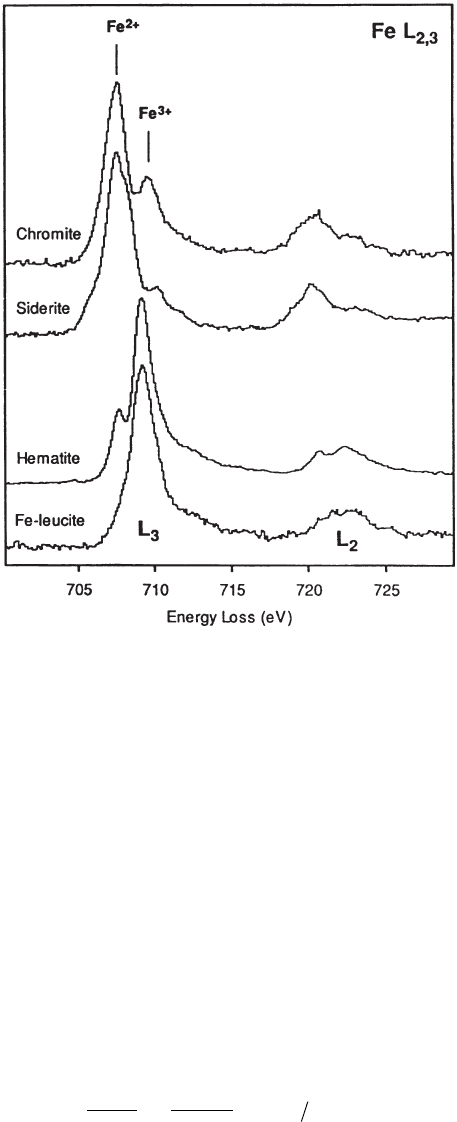
Figure 4–94. Examples of near-edge structures in (a) various carbon-based

compounds showing the sensitivity to the structural environment and hybrid-

ization and in (b) Fe-based compounds. (From Garvie et al., 1994.)

Chapter 4 Analytical Electron Microscopy 387

are therefore observed for several metals with oxidation states for both

X-ray absorption spectroscopy (Chen, 1997) and for EELS (e.g., Mansot

et al., 1994). Detailed reviews on applications of ELNES can be found in

Botton (1999), Keast et al. (2001), and Garvie et al. (1994). Examples dem-

onstrating the application of ELNES at high spatial resolution are given

in Batson (1993), Muller et al. (1999, 2004) and Spence (2005).

At a more quantitative level, the sensitivity of the ELNES to bonding

can be explained by the general oscillator strength and the form factor

terms of the partial cross sections (Section 3.3). These two terms are

dependent on the initial and ﬁ nal state wavefunctions of the interact-

ing electrons and thus contain information on the chemical state and

electronic structure of the probed atoms as modiﬁ ed in the solid. In

the dielectric formulation of the cross sections (Section 3.3.1), it is also

possible to understand how the energy loss spectrum relates to other

spectroscopy measurements:

ddE

θθ

Ω

∝













−

(

)

[]

,Im

(82)

where ε is the dielectric function of the material (Section 3.3.1), which

can be expressed by its real part ε

(related to the screening process of

Figure 4–94. Continued

388 G. Botton

the electrons) and its imaginary part ε

(related to the absorption

process and thus to optical and X-ray absorption measurements). The

ﬁ rst term in Eq. (82) is general and is related to the kinematics of scat-

tering. It imposes a simple Lorentzian angular distribution to the scat-

tering and the rapid drop in intensity with increasing scattering angle.

The second term is the loss function, which is related to the dielectric

response of the solid to an electromagnetic radiation and is therefore

ultimately linked to the intrinsic properties of the solid. At high energy

losses (from about 50–100 eV and above) where the screening of the

incident electron charge by collective effects is not important, ε

→ 1

and ε

is small (ε

<< ε

) so that the loss function is reduced to Im(−1/ε)

= ε

/(ε

+ ε

) = ε

and is thus directly related to the absorption part of

the dielectric function and therefore to absorption measurements. In

this particular condition and in the one electron approximation, the

cross section can be calculated based on Fermi’s golden rule describing

the transition rate of an electron from an initial energy level i described

by an initial wavefunction ψ

of energy E

to a ﬁ nal level f described by

a wavefunction ψ

of energy E

ddE

iEEE

Ω

ΨΨ∝⋅

(

)

−+

(

)

∑

exp qr

(83)

where we have omitted the ﬁ rst (kinematic) term from Eq. (82) because

it is independent of the solid state effects. As deﬁ ned in Section 3.3, the

scattering vector q = k

− k

where k

and k

are the incident and ﬁ nal

wavevectors of the incident electron. The exponential operator is derived

from the Hamiltonian describing the interaction between the incident

electron, the nucleus, and the atomic electrons in the solid [see Paxton

(2005) for a detailed derivation of this term]. The sum is carried out over

all possible ﬁ nal energy states limited by the δ function to ensure the

conservation of energy in the scattering event so that the energy loss E

corresponds to the difference in the energies of the ﬁ nal and initial

states. The exponential operator can be expanded as a Taylor series

exp(iq ⋅ r) = 1 + iq ⋅ r +

–

(iq ⋅ r)

. . . (84)

The ﬁ rst term of this expansion is zero due to the orthogonality of

the initial and ﬁ nal wavefunctions (i.e., 〈ψ

|ψ

〉 = 0). For most conditions

used in EELS experiments (i.e., small spectrometer collection angles β

and edges above around 100 eV), only the term related to dipole excita-

tion q ⋅ r is retained because the scattering angles are small and the core

wavefunctions are very localized in typical EELS experiments. In these

conditions, q ⋅ r << 1 leads to what is known as the dipole approximation

and the second term in the Taylor expansion can be neglected (the

treatment is thus similar to X-ray absorption spectroscopy). For larger

scattering angles or/and for very low core losses (the core state wave-

functions are less and less localized as the core energy decreases, i.e.,

the mean radius of the core wavefunction increases), this approxima-

tion is, strictly speaking, no longer valid but it gives a good representa-

tion of the spectra [nonetheless, full calculations with nondipole terms

are possible with current methodologies (Blaha et al., 2001)]. In the

dipole approximation, we obtain

Chapter 4 Analytical Electron Microscopy 389

ddE

EE E

Ω

ΨΨ∝⋅ −+

(

)

∑

(85)

The squared term is the dipole matrix element representing the transi-

tion rate from a core state to a ﬁ nal state. In this condition, the sum in

Eq. (85) is simpliﬁ ed as

ddE

ME EME E

ρρ

Ω

∝

() ()

−− ++   ,,

(86)

where ρ(E) is the density of states (DOS) resolved in angular momen-

tum components 艎 (s, p, d, f). In the development of the matrix elements

of Eq. (85), the decomposition of the wavefunctions in radial and

angular terms imposes two very interesting effects summarized by Eq.

(86). The radial part of the matrix elements reveals that for a transition

to be observed (i.e., M ≠ 0), there must be an overlap between the core

states and the ﬁ nal state wavefunctions. This implies that the energy

loss spectra probe the site-dependent electronic structure projected on

the excited atom. Practically speaking, since the core states are very

localized, the information is also very local and is not limited just to

the electron beam illuminated area but is speciﬁ c to the atom type

excited by the electron beam: different atoms in the same area illumi-

nated by the electron beam will have a different “local” electronic

structure environment. Second, from the development of the angular

parts of Eq. (85), the matrix element of a transition from a state of

angular momentum component 艎 is zero unless the ﬁ nal state is of

angular momentum 艎 ± 1 as suggested by the subscripts in Eq. (86).

Hence, transitions will therefore occur for states with a change in

angular momentum component ∆艎 = ±1. This implies that if the initial

state is of s character (艎 = 0), the transition will occur only to states of

p character (艎 = 1). This is observed for K edges where the core state is

1s. For an initial state of p character (艎 = 1), transitions will be observed

to states of s (艎 = 0) and d character (艎 = 2). This applies to L

edges

arising from the 2p

3/2

and 2p

1/2

initial states.

The matrix elements therefore allow us to probe the local DOS of each

element separately by selecting the edge corresponding to the atomic

number of the element of interest and the edge type (K, L, etc.) accord-

ing to different principal and angular momentum quantum numbers.

This latter sensitivity is very illuminating since EELS experiments

allow us to probe not only the unoccupied states but also the atom-site-

speciﬁ c and symmetry-projected density of unoccupied states.

The calculations of near-edge structures using Eq. (86) have been

demonstrated to be equivalent for XANES and ELNES in most experi-

mental collection conditions respecting the dipole approximation. The

only difference in the formulation between XANES and ELNES derives

from the fact that the scattering vector q is replaced by the electric ﬁ eld

E in Eqs. (84) and (85). The ELNES is therefore an extremely powerful

probe of the electronic structure of solids with high spatial resolution

as compared to other valence or conduction band spectroscopies in

which the entire bands (valence or conduction) are probed irrespective

of the angular momentum character.

390 G. Botton

The calculations based on Eq. (86) with density of states determined

by ﬁ rst principle methods assume an inﬁ nite lifetime of the excited

state. To account for more realistic conditions where the decay occurs

via deexcitation processes, a ﬁ nite lifetime must be considered. This

can be achieved artiﬁ cially by broadening the δ function with a Lorent-

zian distribution to account for the ﬁ nite lifetime of the excited state,

the lifetime of the core state, as well as the instrumental function

accounting for the energy spread of the incident electrons and the reso-

lution of the spectrometer.

The derivation of Eqs. (83)–(86) has been described here very brieﬂ y

and we refer the interested reader to the work of Fink (1992), Vveden-

sky (1992), Saldin (1987), and Schattschneider and Jouffrey (1995) and

more recently a review by Paxton (2005) for further details. It is impor-

tant to mention, however, some of the limitations of this description to

give an idea of what can be expected from ﬁ rst principle calculations.

First, the one electron derivation of the transition probability is based

on the “single particle” approach. This simpliﬁ cation assumes that the

excited state (where there is a hole in the core state and an ejected

electron) can be represented by ground state wavefunctions (no excita-

tion effects are accounted for). This most important approximation can

be improved on, in principle, by considering the ﬁ nal state rule pro-

posed by von Barth and Grossmann (1982), which considers the elec-

tronic structure of the system in the potential probed by the ejected

electron, i.e., with a core hole in the initial level. In spite of this approxi-

mation, the single particle approach is a ﬁ rst useful step in understand-

ing general features in the spectra and in assessing the need for more

reﬁ ned models accounting for the more realistic ﬁ nal state. For many

systems including metallic materials and even some insulators where

the screening of the core hole is effective, this description is successful,

whereas in others, the interactions between the core hole and the

ejected electron signiﬁ cantly modify the ground state electron wave-

functions of the solid.

A second limitation is related to the speciﬁ c approaches used to

describe the electronic structure of the solid. The predictions of the

DOS are based on the use of density functional theory and the different

implementations to calculate the electron wavefunctions (for a review,

see Hébert, 2006). For the most part, electronic structure calculations

for solids have focused on the description of occupied states and low-

lying unoccupied states. This presents a limitation for the calculations

of energy loss spectra that probe unoccupied states 10–30 eV above the

threshold (and thus above the Fermi energy). To simplify the computa-

tion, linear band structure methods are often used (such as linear

mufﬁ n tin orbital methods and linear augmented plane wave), only a

limited energy range will be reproduced (5–20 eV from the edge thresh-

old). Alternatives to these techniques are the multiple scattering-based

techniques such as the Korringa–Kohn–Rostoker method [(used for

transition metal edges (Botton et al., 1997)], the real space multiple

scattering technique (Ankudinov et al., 1998), and the pseudopotential

technique based on the use of plane waves that has produced impres-

sive results at about 40–50 eV above the threshold in diamond (Pickard

and Payne, 1997).

Chapter 4 Analytical Electron Microscopy 391

In addition to these calculations of ELNES based on band structure

techniques or real space methods, other approaches must be used to

deal with systems demonstrating strong electron–electron interactions

due to the localization of the electrons. For these systems the band

structure and real space methods fail to describe the spectra and a

different scheme must be used. For transition metals L edges and rare-

earth M edges, a description based on atomic multiplet theory is much

more effective in describing the spectra. These techniques include

solid-state effects by including crystal ﬁ eld and charge transfer effects

to describe the structural and bonding environment. A full description

of the methods is given in the excellent reviews by deGroot (1994, 2005).

Examples of calculations with this technique and a range of other

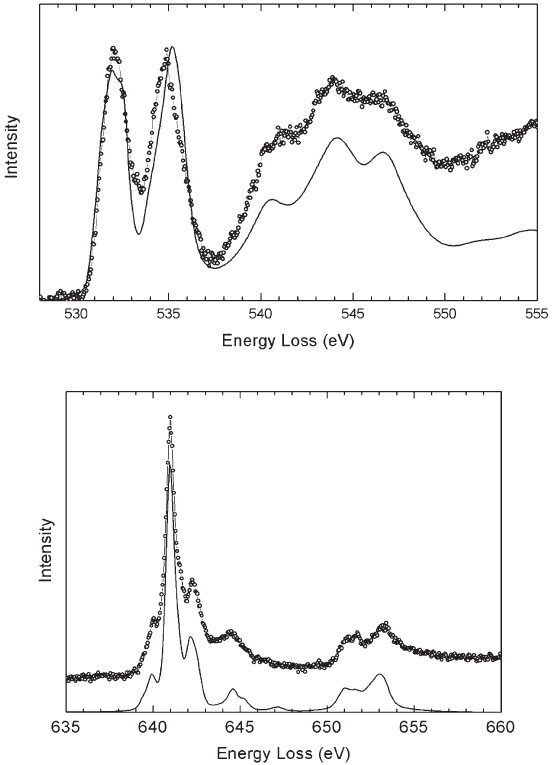
methods are shown in Figure 4–95. A description of the hierarchy of

these methods starting from the molecular orbital approach and mul-

tiple scattering methods can be found in Rez et al. (1995).

In addition, the ﬂ exibility of EELS experiments in the TEM makes it

possible to tune very effectively and elegantly the scattering vector of

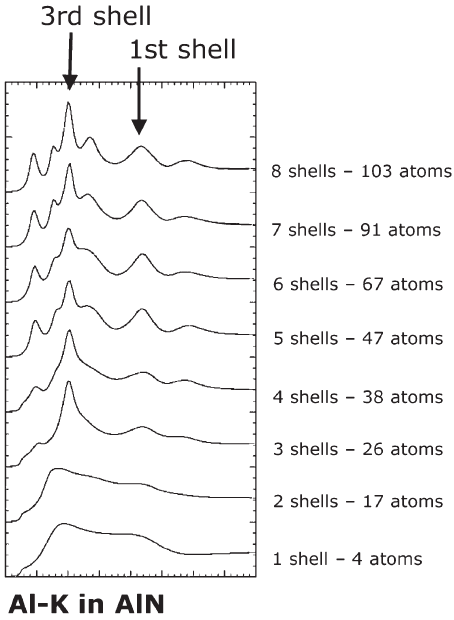
Figure 4–95. Examples of calculations of ELNES with (a) the multiple scatter-

ing method for the Al K edge in AlN and (b) bandstructure technique: O K

edge in rutile experiments (dots) and calculations (full line) with abinitio code

Wien2K. (Spectrum courtesy of P. Tiemeij er, FEI.) (c) Atomic multiplet calcula-

tions of the MnL

edge in MnTiO

. (Courtesy of G. Radtke, McMaster

University.)

392 G. Botton

the incident electron using momentum-resolved energy loss experi-

ments to study anisotropic materials. Experiments demonstrating this

effect in low-loss spectra (Fink, 1989, 1992) and core losses (Radtke et

al., 2003; Botton et al., 1995a; Jouffrey et al., 2004) and to record inelastic

scattering distributions (Botton, 2005) can be found in the literature.

Various tools are therefore available to materials scientists and

microscopists with which to understand and model near edge struc-

tures should the need arise. In many cases of AEM applications,

however, a detailed comparison of various edges with reference mate-

rials is sufﬁ cient to understand the trends and associate the spectral

features to bonding bands and materials properties. Databases are

currently in development allowing users to access libraries of spectra

from various compounds: http://www.cemes.fr/~eelsdb and http://

people.ccmr.cornell.edu/~davidm/WEELS.

Figure 4–95. Continued

Chapter 4 Analytical Electron Microscopy 393

8.2 Low-Loss Spectroscopy

8.2.1 Fundamentals

At low energy losses (0 to 50–100 eV), the most intense part of

the spectrum is directly related to the collective response of the

electrons in the solid to the fast incident electron. The incident

charges with their associated electric ﬁ eld polarize the medium

and set up oscillations of the weakly bound electrons of the solid at

particular eigenfrequencies related to the mass of the electrons and

their density in the solid. This is analogous to the resonance frequency

of an object of mass m attached to a spring with spring constant k of

classical mechanics. The collective behavior of these electrons in a

solid is best characterized by treating the collective response as

an effective particle called plasmon oscillating at a frequency ω

that

results in an energy loss of the primary electron equivalent to the

energy E

= h

The link between the spectrum, the general oscillator strength, and

the loss function presented in Section 3.3.1 can be discussed in the

context of low energy losses. Whereas at high energies (Section 8.1) the

loss function is essentially determined by ε

, at low energies the screen-

ing of the electrons is very effective and |ε

| becomes much greater (in

simple metals) than (or is about the same order of) ε

. The loss function

Im(−1/ε) = ε

/(ε

+ ε

) must then consider both the polarizability and

the absorption terms essentially describing the dielectric response of

the solid to electromagnetic radiation.

Detailed derivations of the models describing the formulation of the

dielectric response have been reviewed by Schattschneider and Jouf-

frey (1995) and Raether (1980) and only a brief summary is given here

to explain the most signiﬁ cant features in the spectra and the relation

to the dielectric response of the medium.

The Drude model is the simplest case that deals with free-

electron metals and the dielectric function of the material. This

model considers electrons in the solid as free particles interacting with

the medium via a simple damping term τ describing the relaxation

time due to friction in the electron gas. The dielectric function then

becomes

εω

ωωτ

()

=− ⋅

(

)

(87)

where we deﬁ ne the term

(88)

as the eigenfrequency of the electron plasma oscillation with

εε

ωτ

εε

ωτ

{}

=−

()

{}

=−

()

Re Im

and

(89)

τ is related to the FWHM of the plasmon peaks ∆E

= h

/τ, m is the

effective mass of the electrons, ε

is the vacuum dielectric constant, and

is the free electron density and the plasmon energy

394 G. Botton

==ω

(90)

The free-electron model, although very applicable for many sp metals,

is not realistic for all materials or even all metals. To treat the full range

of transition metals, insulators, and semiconductors more realistically,

there must be provision for transitions from various occupied to unoc-

cupied bands in addition to contributions from the free electrons. This

is done in the Drude–Lorentz model where discrete transitions are

added by considering independent oscillators having eigenfrequencies

equal to the transition energies (for example, to account for band-to-

band transitions related to d electrons and interband transitions from

the valence to conduction band). The expression contains the free oscil-

lators (such as the Drude oscillators) and the “bound” oscillators. The

dielectric function is therefore the sum over all these oscillators “j”:

εω

ωω ωτ

()

−−

(

)

∑

(91)

where n

is the number of electrons able to oscillate at the eigenfre-

quency ω

The presence of oscillators due to interband transitions or low-energy

edges causes the peaks in the absorption part of the dielectric function

and generates shifts in the position of the plasmon peaks. Similarly,

the effect of the plasmon peaks is to shift the apparent energy of the

interband transitions in the energy loss spectra with respect to the

energy in the absorption part of the dielectric function. Such shifts

therefore imply that caution should be taken when interpreting peaks

in spectra: the position of a peak at a given energy loss E does not imply

that there is an interband transition with same exact energy E.

8.2.2 Applications

The effects discussed in the previous section, even if not always fully

quantiﬁ ed in analytical electron microscopy work, can be exploited in

energy-ﬁ ltered “plasmon” images to identify the presence of phases

with different electron densities (hence plasmon position) or dielectric

function. Systematic variations of the plasmon energy as a function of

the atomic number have been demonstrated in the early work of Colliex

(1984) (Figure 4–96). Plasmon energies in alloys and metallic hydrides

as a function of alloying element concentration and hydrogen content

have been tabulated from various sources in Egerton (1996). This tech-

nique of plasmon measurement has also been applied to study the ratio

of sp

/sp

hybridization bonding in C ﬁ lms and the water content in

biological structures (Figure 4–81) (Sun et al., 1995).

Although a detailed analysis of the low-loss spectra is not yet a

routine AEM techniques, detailed study of spectra can be extremely

useful to understand some of the functional properties of materials.

For examples, the relationship between the spectrum and the dielectric

properties of solids can help elucidate some local variations of optical

properties of materials (Turowski and Kelly, 1992; Schamm and Zanchi,

2003; Mullejans and French, 2000). Such studies make use of some key