Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 4 Analytical Electron Microscopy 375

analysis area and represents the lowest concentration that can be

detected. The minimum detectable number (MDN) refers to the smallest

number of atoms that can be detected. This applies to analyses in which

these atoms are clustered (such as biological molecules containing few

atoms, atomic clusters, etc.) or very small probes are used and only a few

atoms of impurity are being analyzed in the interaction volume.

Predictions of the MDF are related to the process of signal generation

(incident number of electrons, cross sections, ﬂ uorescence yield), col-

lection efﬁ ciency of the detector system (solid angle, detector quantum

efﬁ ciency, noise), sample characteristics (thickness, scattering outside

apertures leading to loss of signal, background signal, and signal

extraction variance), and potential sources of noncharacteristic signals

arising from the instrument.

The overall principle for estimating the MDF is based on the statisti-

cal certainty of detecting a signal above a background containing some

noise due to the variance in the background intensity. This detection

is based on the Rose visibility criterion (Rose, 1970) which states that

the signal should be three times the standard deviation of the back-

ground (the noise) for reliable identiﬁ cation of the signal as genuine in

a 98% conﬁ dence level. This criterion ensures that the signal can be

clearly distinguishable from a simple statistical variation of the back-

ground with a high degree of conﬁ dence. This general criterion is

applicable in both EELS and EDXS measurements (as in any other

signal processing method).

7.1 Detection Limits for EDXS

We can describe the evaluation of the MDF for EDXS as follows. Assum-

ing that the noise in the background signal follows a Poisson statistical

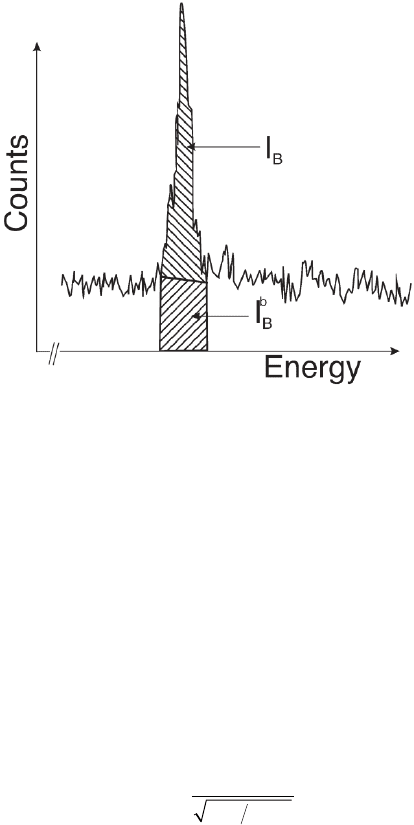
distribution, the minimum detectable signal for element B (I

min

) in

EDXS measurements is

bmin

≥⋅32

where the square root term rep-

resents the variance of the background signal under the peak of element

B (I

), i.e., the noise (Figure 4–86). Experimentally, the detection limit

of an element B in a matrix A can easily be determined by using a

standard of known composition C

and the detected signal I

. The MDF

is the concentration resulting in a minimum signal-to-noise ratio (SNR)

= 3, hence

SNR I I I

std

=− ⋅()2

and SNR

MDF

= 3 (the SNR corre-

sponding to the Rose criterion and the MDF). This resulting concentra-

tion yielding an SNR = 3 is the minimum detectable fraction:

MMF

⋅⋅

−

(71)

If the standard containing element B is not available, we can still

retrieve the detectable fraction based on a pure element A standard

using k

factors (see Section 4) and by assuming that the background

under the peak of element B (if it was present) is not signiﬁ cantly

altered when this element is in trace concentration in a sample. In this

case, we obtain

kII

MMF

AB A

⋅⋅

−

()

(72)

376 G. Botton

where I

is the background under the peak of element A and C

is the

concentration of element A (assumed to be 1 if the standard is pure).

From this simple empirical treatment it can be seen that improve-

ments in detection limits (i.e., lower values) can be achieved by increas-

ing the peak intensity (through a longer acquisition time and/or larger

probe current) and by reducing the background. This latter contribu-

tion is affected by sample thickness, instrument operating conditions,

and instrumental contributions (discussed in Section 7.2). The general

treatment required to understand the trends in detection limits is due

to Ziebold (1967), who related the MMF to microanalysis conditions

(Goldstein et al., 1986)

MMF

PPBn

∝

(

)

(73)

where P is the peak above the background count rate, P/B is the peak-

to-background ratio (with integration of the background deﬁ ned over

the same energy window as the peak), n is the number of analyses, and

τ is the acquisition time for each analysis carried out. It is possible to

increase the peak counts by increasing the electron beam current, the

thickness of the sample, and the collection efﬁ ciency (larger solid angle

of the detector) while increasing the P/B ratio by increasing the accel-

erating voltage of the microscope and reducing the instrumental con-

tribution leading to noncharacteristic signals. Although a large fraction

of the background arises from bremsstrahlung radiation in the sample,

signiﬁ cant contributions can come from spurious signals arising from

electrons scattered at high angles (including backscattering), which, in

turn, generate X-rays within the column. An additional contribution to

the background arises from hard X-rays generated in the condenser

lens system—when electrons hit apertures in the optic path—that ﬂ uo-

Figure 4–86. Deﬁ nition of peak and background intensities in EDXS spectra.

The peak intensity is deﬁ ned with respect to intensities just beside the peak.

Chapter 4 Analytical Electron Microscopy 377

resce X-rays in the specimen area, including the sample holder. Such

spurious signals are known as instrumental contributions.

As discussed above, increased count rates for a given spot size can

be achieved through brighter electron sources (Section 2.1) and thicker

samples, although the latter will also lead to increased undesired con-

tributions (increase in background) and loss of spatial resolution

(Section 5). Increased total analysis time nτ can be achieved only if the

sample is stable under the electron beam (due to electron beam damage,

contamination, etc.) and sample drift is minimal or can be corrected

via alignment algorithms. A clean vacuum system and clean samples

are of the utmost importance. Dry pumping systems, bakeable columns,

clean sample holders always kept in vacuum, and plasma cleaning of

the samples prior to the TEM sessions are key components of improved

analytical performance of the microscope and are ultimately as impor-

tant as the quality of the EDXS detector and the microscope. With the

use of analytical electronic microscopes equipped with small electron

beams, thin samples, and more recently aberration correctors, it has

been possible to achieve fractions of 1% detection with subnanometer

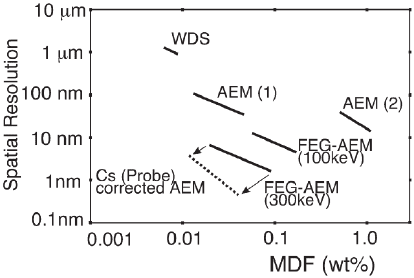
spatial resolution (Figure 4–87) (Watanabe and Williams, 2005a).

7.2 Instr umental Contributions in EDXS

These spurious signals can be minimized by improvements in the

column, detector, and sample holder designs. For example, a signiﬁ cant

reduction in hard X-rays generated in the upper part of the column can

be achieved by using thick top-hat-shaped Pt apertures. These are now

available in most modern analytical microscopes as part of the selection

of C

apertures (some might just be Mo or lighter elements allowing

transmission of hard X-rays). Good collimation of the detector is also

important to minimize the line of sight between the specimen and the

active area of the detector so that X-rays generated elsewhere in the speci-

Figure 4–87. Detection limits reached in modern AEM and various examples

of performance reached with different instruments. WDS is data obtained

with a dedicated microprobe (30 keV), AEM (1) 120 keV, AEM (2) 100 keV, LaB

instruments, 100 keV FEG, 300 keV (Watanabe and Williams, 1999), and

aberration-corrected FEG. (Adapted from Watanabe and Williams, 2005a, and

Williams and Carter, 1996.)

378 G. Botton

men chamber area by scattered electrons reaching apertures, the pole-

piece of the objective lens, do not reach the detector (Figures 4–23 and

4–88). Using small samples (rather than the standard 3-mm disks with

bulk edges) also minimizes the contributions due to ﬂ uorescence and

electron scattering (electrons returning back to the sample after hitting

parts of the column). Finally, the sample holder must be designed for

analytical purposes (these are available commercially), namely, built

with light element materials, ideally Be as one of the main components

in the specimen supporting area, with a Be ring to tighten the sample and

a design geometry allowing the acquisition of spectra without signiﬁ cant

tilt of the sample (Figure 4–89). This conﬁ guration leads to minimal

instrumental contributions so that X-rays generated in the sample have a

Figure 4–88. Instrumental contributions to the characteristic signals detected

from the sample. Spurious X-rays are produced by the scattered electrons

interacting with the microscope components (labeled 1, 2, 4). Spurious signals

are also produced by hard X-rays generated on the top part of the column

hitting the sample holder, grid, and other parts of the specimen chamber

(labeled 5, 6, and 3). Nonoptimal collimation allows X-rays generated other

than the sample area to reach the detector (compare with Figure 4–23).

Figure 4–89. Sample

holders for AEM (top)

JEOL 2010F microscope

holder and (bottom)

Philips/FEI CM-Tecnai

series holder with

machined grove for

minimal tilt of sample.

Chapter 4 Analytical Electron Microscopy 379

direct line of sight to the detector without being absorbed (and causing

ﬂ uorescence) in the sample holder. Sample grids made of Cu (or other

metals such as Ni or Mo) to support continuous, lacey or holey C ﬁ lms

where the sample is distributed (in the form of dispersed particles, repli-

cas, or lift-out focused ion beam samples) generate signiﬁ cant spurious

signals as shown by the presence of peaks of the grid material even if the

electrons are not directly illuminating the grid. Recently, diamond grids

have been developed to minimize these contributions when these prob-

lems affect the analysis. In many cases, the selection of the grid material

can be made judiciously to avoid quantiﬁ cation problems given the com-

mercial availability of several grid materials.

Based on these instrumental considerations, the overall quality of

the microscope analytical performance can be evaluated with measure-

ments of the “hole-count” signals. By measuring the signal generated

when the electron beam is directed into the hole of the sample, contri-

butions from the grid, the microscope chamber, and holder can poten-

tially be observed (and identiﬁ ed from the element present) and should

be, in a good analytical TEM, less than 1% of the signal generated on

the sample. Quantitative evaluation of the performance can be carried

out using standard samples of Cr (100 nm thick) and NiO and well-

deﬁ ned tests based on P/B ratios (Williams and Carter, 1996; Egerton

and Cheng, 1994). Overall, low instrumental contributions lead to

lower peak-to-background values and improved detection limits. Well-

designed analytical microscopes (Section 2.3.6) and the use of analyti-

cal conditions (correct analytical apertures, sample geometry, tilt) lead

to signiﬁ cantly improved detection limits.

7.3 EELS Detection Limits

The basic statistical principle for detection of signals used in EDXS (the

Rose criterion) is also applicable in the case of EELS. The empirical

approach to estimate the detection limit based on experiments and

known standards is the same as in EDXS but with additional complica-

tions due to the determination of the noise component arising from the

extrapolation of the background rather than the simple interpolation.

The noise, and thus the SNR, cannot be determined based on the

simple variance of the number of counts at a given energy loss. The

noise must be estimated directly from a detailed statistical analysis of

the spectra and the errors related to the determination of the extrapola-

tion parameters (Trebbia, 1988) or simpler approximations of the

extrapolation error based on the width of the ﬁ tting and extrapolation

windows (Egerton, 1996).

From ﬁ rst principles, it is possible to estimate the detection limits

accounting for these statistical effects and physical principles as

described in detail by Egerton (1996) and Egerton and Leapman (1995).

The variance of the signal must take into account the error due to the

extrapolation of the background under the edge and the introduction of

noise related to the detective quantum efﬁ ciency (DQE) of the spectrom-

eter. The DQE is deﬁ ned (Krivanek et al., 1987; Egerton, 1996) as SNR

output

SNR

input

(where the indices “input” and “output” are based on the

380 G. Botton

incident counting statistic and measured statistic, respectively) and

varies with the number of incident electrons, but, for the purpose of our

estimations, is assumed constant and not equal to one as generally

assumed in the case of EDXS spectra. The determination of the

EELS detection limits must also include the effect of elastic scattering

reducing the efﬁ ciency of collection of the signals due to scattering

outside the aperture. Accounting for the detector response, the SNR is

(Egerton, 1996),

SNR DQE

≈

⋅

(74)

where I

is the background under the edge, h is an error parameter due

to the extrapolation, and I

is the integrated edge intensity. Large ﬁ tting

intervals close to the edge threshold and small integration windows

lead to small h parameters (around 5–10), while small ﬁ tting intervals

further from the edge and large integration windows result in large h

values (as large as 20–30) (Egerton, 1996). The number of electrons

causing a signal is related to the dose D [coulomb/(unit area)] and the

area illuminated by a probe with diameter d as

I(β,∆) ≈ (π/4)d

(D/e)exp(−t/λ

) (75)

where the exponential term represents the loss of electrons following

elastic scattering outside the collector aperture β in a specimen of

thickness t relative to the elastic mean free path λ

. The background

signal (I

) related to the number of atoms of the matrix N

and the

number of atoms of the trace element N giving rise to edge signals I

are related to the respective cross sections and the number of incident

electrons and number of atoms in the volume as

≈ N

I(β,∆)σ

(β,∆) and I

≈ NI(β,∆)σ

(β,∆) (76)

Since the fraction of trace element f = N/N

we obtain

SNR h

DQE=

()













()

−

σβ

,∆

∆

(77)

The MDF is the fraction f

min

corresponding to an SNR = 3 (as in the

case of EDXS following the Rose criterion). This yields (Egerton,

1996)

MDF f

DQE D e N

=≈

()

(

)

()

(

)















min

exp

311

σβ

∆



)

(78)

The minimum detectable number quantity is related to the number of

atoms within the analyzed area corresponding to the minimum detect-

able fraction determined above:

MDN d f N

dNh

DQE D e

=≈

()

(

)













σβ

min

exp

∆

λλ





)

(79)

By calculating the various cross sections (Section 3), detection limits

can be estimated. Assuming a DQE ≈ 0.5 typical of parallel spectrome-

ters, h = 9, λ

= 200 nm, a carbon matrix of 30 nm thickness, based on the

Chapter 4 Analytical Electron Microscopy 381

expression given above (Egerton, 1996) calculated the detection of Ca

atoms for a range of doses using 100 keV electrons and hydrogenic cross

sections. The detection of a few atoms within a 1-nm probe is possible

assuming the sample can withstand doses of the order of 10

C/cm

. For

elements with large cross sections (such as L and M lines) detection of

a few ppm has been demonstrated (Leapman and Newbury, 1993) while

higher detection limits are possible for K edges and delayed edges of

elements such as Ag, Au, and S. A signiﬁ cant improvement in the detec-

tion limits is achieved if the spectra are processed using multiple least-

squares analysis of data acquired in spectral-difference mode (see

Section 4.2.1) where reference data are ﬁ tted to the experimental spec-

trum. This approach results in a much lower signal extraction error

with h values approaching 1. Detection of single atoms of thorium was

demonstrated by Krivanek et al. (1991b) and individual Gd atoms were

detected by Suenaga et al. (2000). More recently, systematic work on Ca

and Fe containing molecules demonstrated elemental maps with the

detection of just a few (7–8) base pairs of a DNA molecule under the

electron beam (within the pixel size) containing 14–16 P atoms and 4

atoms of Fe in the one single hemoglobin molecule (Leapman and

Rizzo, 1999) and single Ca atom detection (Leapman, 2003). Experi-

ments demonstrating detection of a few ppm in standard reference

materials of known composition have been reported by Leapman and

Newbury (1993), Newbury (1998), and Newbury et al. (2000) (Figure

4–90). The work assumes detection of the edges based on spectral dif-

ference technique (Section 4.2.1), parallel detection spectrometers, and

very long acquisition times. These detection limits also assume very

thin samples, typically t/λ < 0.3–0.5 (see Section 4.2.4). If thicker samples

are used, the detection limits degrade signiﬁ cantly up to the point at

which even pure elements would not be detected in samples as a result

of the increase in the background due to multiple scattering (Section

8.2) that masks the edges. A summary of the detection limits based on

the work of Leapman and Newbury (1993; Newbury, 1998; Newbury

et al., 2000) is presented in Table 4–6.

A detailed simulation package predicting the detection limits includ-

ing the effects of increased background, multiple scattering, and

angular collection has been developed commercially (available by

Gatan as the “EELS advisor”) based on the initial work of Natusch

et al. (1999) and Menon and Krivanek (2002). Applications of these

simulations are extremely useful in predicting whether elements

present at low concentration levels in any matrix can be detected and

in suggesting experimental conditions to detect these elements.

7.4 Comparison of EELS and EDXS Detection Limits

An expression for the detected X-ray signal based on the incident

current I and acquisition time T can be deduced so that the relative

merits of EDXS and EELS can be compared (Egerton, 1996).

Following the description given for X-ray signal quantiﬁ cation

(Section 4.1) we describe the intensity

= N(I/e)Tω

(80)

382 G. Botton

Figure 4–90. Extraction of signals using the second-difference technique for the detection of trace

concentration of reference materials in a standard sample (SRM 610 glass from NIST). (Reprinted from

trace constituents are not visible. In the second difference spectrum (bottom) the edges of trace ele-

ments are well resolved. Elements Ba, La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, and Yn are present

in the 60–80 ppm range. Sc, Ti, V, Cr, Mn, Fe, and Co are present in the 150–240 ppm range.

Table 4 – 6. Edge shapes and labels for elements of the periodic table as detectable in EELS

experiments.

Edge type (following the Gatan

Detection limit Element and edges chart convention)

10–100 ppm 3d transition metals and preceding

alkaline earth elements: L edges

(Ca, Sc, . . . Ni)

4f lanthanides and preceding

alkaline earth elements M

edges

(Ba, La, . . . Yb)

100–1000 ppm (0.1%) Light elements:

K edges (Li, Be, B. . . . P)

edges(Mg, Al, Si, P, S, Cl)

4d transitionmetal elements and

preceding alkaline earth elements

edges (Sr, Y, . . . Rh)

>1000 ppm (0.1%) Ga, Ge, As, Se, Ag, Cd, In, Sn,

Sb, Te, I, W . . .

Chapter 4 Analytical Electron Microscopy 383

where ω

is the ﬂ uorescence yield for the particular line, σ

is the total

cross section (integrated over all the angles; see Section 3.4.2), and η

is the collection efﬁ ciency including all the detector components and

any absorption in the sample.

The relative sensitivity of EELS and EDXS signals can be calculated

by discussing the ratio of EELS and EDXS intensities

kk x

()

−





)

σβ

ωσ η λ

∆ 1

exp

(81)

The ratio of the partial and total cross-sectional term is typically in the

order of 0.1 (Egerton, 1996), although large scattering angles and energy

windows (∆ > 50 eV) would tend to include most of the inelastic distri-

bution given the asymptotic behavior of the scattering distribution and

the cross sections (Section 3.4). The ﬂ uorescence term is the major

contributor to the greater effectiveness of EELS for the detection of a

large number of elements in “ideal” samples. For K edges of heavy

elements with Z > 40 (difﬁ cult to reach in TEM-EELS experiments

given their high energy loss), ω approaches 1 (Figure 4–49), but for

light elements or L edges, it drops very sharply (for K edges it is around

0.1 for Al, 0.02 for Na, down to 0.001 for B, while for L edges it is less

than 0.001 for Z < 20). The detector efﬁ ciency term also has a signiﬁ cant

effect on the relative merit of EELS. The small solid angle of the EDXS

detector implies that only 1% of the emitted X-rays are collected by the

detector. Furthermore, low-energy X-rays can be absorbed in the thin

window and the dead layer of the detector (Section 2.3.2). Due to the

combined terms of ﬂ uorescence and detector efﬁ ciency, the EELS

signals are three to four orders of magnitude stronger than EDXS

signals for light elements while they are slightly stronger for most

heavy elements. The relative merits are summarized in Figure 4–91.

The drawback with EELS, however, is not fully accounted for in Eq.

Figure 4–91. Comparison of the rela-

tive sensitivity of EELS/EDXS detec-

tion limits. Note that the calculations

assume samples are very thin.

(Reprinted from Egerton and Leapman

Science+Business Media.)

384 G. Botton

(81) due to the strong increase of background with thickness arising

from multiple scattering. For thick samples, even of pure elements,

EELS would not show any edge irrespective of the atomic number,

while EDXS spectra would still show peaks (even for light elements,

albeit small)! The absence of EELS edges in a spectrum from just a

sample does not necessarily imply the absence of any elements.

8 Energy Loss Fine Structures

As discussed in the introduction of this chapter, there are ﬁ ne modula-

tions in the structure of spectra that yield useful information on the

chemical environment of the atoms and the dielectric properties of

the material. These ﬁ ne structures can be subdivided into three parts.

The ELNES are modulations appearing in the ﬁ rst 10–20 eV from the

ionization edge threshold (Figure 4–92). These are now used almost

routinely to characterize the chemical environment of atoms, including

the type of phases and valence state.

At higher energy losses (from about 30–50 eV of the threshold up to

several hundred electronvolts), the extended energy loss ﬁ ne struc-

tures (EXELFS) provide information on the radial distribution function

of the material [similar to X-ray absorption ﬁ ne structures (XAFS)]

(Figure 4–92). These modulations arise from the backscattering of the

ejected electron in the solid and the creation of interference between

the ejected and backscattered wavefunctions and are particularly

useful in providing the bond distances in amorphous solids at a nano-

meter scale. Since current applications of the technique in the AEM

literature are limited we will refer the reader to a good overview of

this technique in Egerton (1996) and to XAFS literature describing the

principles of the analysis method.

Finally, the ﬁ ne modulations in the low-loss part of the EEL spectra

(from 0 to 50–100 eV) also provide a wealth of information on the

dielectric properties of materials. Quantitative analysis makes it pos-

sible to compare optical spectroscopy measurements to low-loss energy

loss data and measure electron density using some simple approxima-

tions for metals. Qualitative analysis allows us to use the differences

in spectra for various materials to map the distribution of phases.

Given the impact of the ELNES and low-loss spectra in AEM, details

of these two techniques are presented below.

Figure 4–92. Regions

and energy ranges for

the energy loss near-

edge structures

(ELNES) and extended

energy loss ﬁ ne struc-

tures (EXELFS) of core

edges.