Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 4 Analytical Electron Microscopy 345

correction factors into Eq. (52) that can be deduced analytically (Egerton,

1996) for each particular edge. The relative concentration becomes

(

)

(

)

(

)

(

)

σβ

∆

(53)

where F

1a,b

are the convergence correction factors that are dependent

on the angular scattering distribution for a particular edge via the

characteristic scattering angle θ

. Correction factors must therefore be

calculated for each edge of interest in the quantiﬁ cation and can be

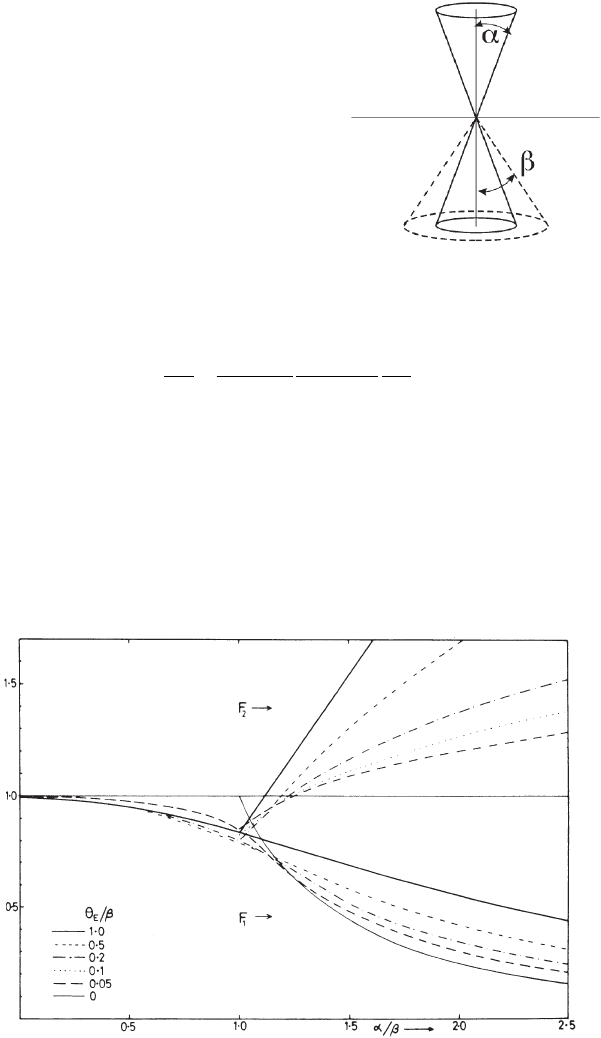
deduced from Figure 4–60 or from simple programs (Egerton, 1996). It

is possible to note that for edges of very similar intrinsic angular dis-

tributions (i.e., two edges close in energy will have very similar θ

) the

Figure 4–59. Relation between the conver-

gence and collection angles for quantiﬁ ca-

tion of spectra accounting for the incident

beam convergence.

Figure 4–60. Correction factors F

useful to quantify spectra accounting for

convergence of the incident beam α. The convergence factors F

must be deter-

mined for each edge based on the convergence angle α relative to the collection

angle β. For each edge, the characteristic angle θ

relative to the collection

angle β must be used to identify the appropriate curve to be used in the quan-

tiﬁ cation. The F

curves are used only for absolute quantiﬁ cation. (From

346 G. Botton

ratio F

is close to one and no effect of convergence is visible irre-

spective of the convergence angle.

For absolute quantiﬁ cation, the correction of the expression relating

the number of atoms and the recorded intensity under the edge

[Eq. (51)] becomes necessary irrespective of the intrinsic angular

distribution

(β,∆,α) ≈ F

NI(β,∆)σ

(β,∆α) (54)

where the correction factor F

≈ F

for α ≤ β and F

= (α/β)

for α ≥ β

and can be deduced from Figure 4–60.

4.2.3 k-Factor Approach

All the expressions for relative quantiﬁ cation in EELS are similar to

the k

factor equations in EDXS microanalysis. In a similar manner, a

k-factor approach has been proposed (Malis and Titchmarsh, 1985) to

quantify EELS spectra, although the experimental and sample condi-

tions (convergence, collection, sample thickness) must be very strictly

controlled and reproducible. Once the k-factor has been determined on

the reference sample accounting for the cross-sectional ratios and pos-

sible convergence effects, the same k-factor can be used to deduce the

composition of the unknown samples as in EDXS microanalysis. Cross

section calculations using the currently available models (Hartree–

Slater or hydrogenic, see Section 3.4) and convergence corrections are

already built-in in commercial programs that control the acquisition

functions of the spectrometers. An additional calculation approach to

deduce the cross sections necessary for the quantiﬁ cation makes use

of tabulations of the oscillator strengths obtained from optical data (see

Section 3.4.1). These methods require the acquisition of spectra in

dipole conditions (i.e., with small collection angles) and within the

energy range where the angular distribution of scattering is still domi-

nated by the Lorentzian term of Eq. (27) (i.e., near the edge threshold).

The methodology is described in Egerton (1993) and summarized in

Egerton and Leapman (1995).

4.2.4 Limitations in Analysis and Quantiﬁ cation

Although EELS quantiﬁ cation is not affected by absorption or ﬂ uores-

cence, there are major drawbacks in quantitative and even qualitative

EELS analysis. The major difﬁ culty is the strong effect of the sample

thickness on the detection of EELS edges. For example, spectra from

specimens of very simple composition a few tens of nanometers in

thickness can reveal well-resolved edges while spectra from “thicker”

areas (as thin as 100 nm) might show no edges (Figure 4–61). This

severe limitation to the visibility of edges is due to the contribution of

multiple inelastic scattering that increases the background under the

edge. The contribution of multiple scattering, however, is not uniform

as a function of energy loss and the quantiﬁ cation of spectra for increas-

ingly thick samples demonstrates a variation of the apparent concen-

tration with thickness. Systematic measurements of the ratio of two

elements, for example, show that samples with thickness relative to the

mean inelastic free path (Sections 3.4 and 8.2) t/λ > 0.5 are unreliable

(Figure 4–62). Even when multiple scattering effects are removed with

Chapter 4 Analytical Electron Microscopy 347

deconvolution techniques (Section 8.2), the effects persist (Egerton,

1996), suggesting that additional contributions due to the angular dis-

tributions of losses are present and cannot be neglected in correction

approaches. Calculations that include the contributions of elastic scat-

tering (Cheng and Egerton, 1993) and convolutions of the energy and

angular distributions of the scattering angle (Su et al., 1995) demon-

strate trends that are consistent with the experimental variation of the

composition with thickness. Correction programs have been devel-

oped to account for these effects (Wong and Egerton, 1995). The lack

of visibility of edges in spectra, even for pure elements, implies that

users should be particularly cautious about drawing conclusions on

the absence of elements during the analysis of point spectra and par-

ticularly with the application of energy-ﬁ ltered imaging techniques.

In the latter condition, since spectra are usually disregarded and the

acquisition is done in an automatic procedure, erroneous results can

often be obtained if care is not taken to check the sample thickness

prior to the analysis of spectra. Relative thickness maps should

therefore be used as a routine check prior to elemental imaging to

verify the applicability of the t/λ > 0.5 condition. The procedure for

the measurement of the relative thickness is described in detail in

Section 8.2.

Figure 4–61. Variation of the

visibility of spectra with increas-

ing thickness of the sample.

Thick samples will not necessar-

ily show EELS edges even for

major constituents.

Figure 4–62. Variation in the

quantiﬁ cation of two elements

as a function of thickness

relative to the total inelastic

mean free path.

348 G. Botton

5 Resolution in Microanalysis

5.1 EDXS Microanalysis

Two contributions determine the spatial resolution in X-ray micro-

analysis. The ﬁ rst contribution arises from the electron beam diameter

and the second from the electron beam broadening generated when

electrons travel in the sample. The early analytical TEMs provided

beam diameters of the order of tens to a hundred nanometers and the

beam broadening within the sample was not a signiﬁ cant issue. Mea-

surements using contamination spots demonstrated that the illumi-

nated area on the top of the sample was essentially the same as the exit

surface of the electron beam (e.g., see Stenton et al., 1981). The situation

changed radically with the development of analytical instruments

equipped with ﬁ eld emission sources capable of achieving probe sizes

in the order of a nanometer or smaller (Section 2.1) whereby the ulti-

mate limits in spatial resolution due to the intrinsic beam broadening

could be probed.

To determine electron beam broadening, we must consider that the

trajectory of the incident beam is controlled by an elastic scattering

process that causes the deviation of the incident electrons as they travel

through the sample. Transport equations (Rez, 1984) and detailed mul-

tislice calculations (e.g., Loan et al., 1988; Mobus and Nufer, 2003;

Voyles and Muller, 2004; Dwyer and Etheridge, 2003; and Section 3.2)

have been developed to describe electron beam propagation [including

the impact of sub-Angstrom beams (Dwyer and Etheridge, 2003)] but

more extensive work has been carried out in the ﬁ eld of AEM using

Monte Carlo simulations that consider the individual trajectories of the

incident electrons, the elastic scattering cross sections that modify the

electron trajectories, and the inelastic scattering that causes the slow-

down of the electrons (Figure 4–63). Monte Carlo approaches are easily

applicable in complex geometries of samples (for example, interfaces

and particles), although they neglect the effect of channeling of elec-

trons in crystal and therefore assume the sample is amorphous or tilted

away from a zone axis. The Monte Carlo technique is based on the

generation of random numbers that are used to calculate the scattering

angles [via equations of the elastic cross sections: Eq. (11)], the path-

length between scattering events [using the elastic mean free path of

Eq. (12)], and the energy loss between the scattering events [using the

stopping power derived from the inelastic cross sections: Eq. (19)].

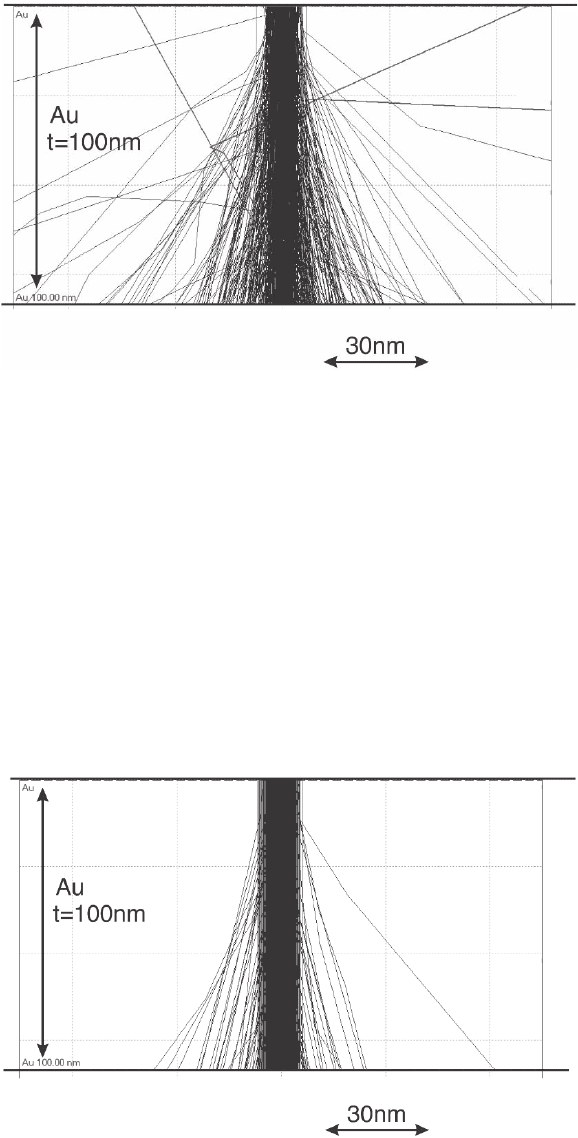
Electron trajectories simulated with the Monte Carlo method for thin

ﬁ lms show the dependence of beam broadening on the accelerating

voltage (Figure 4–64). The effect of the average atomic number and

sample geometry can also be easily determined. With these simula-

tions, it is possible, in principle, to evaluate the exit area and the volume

containing an arbitrary fraction of electrons that will contribute to the

generation of the X-rays signal and thus the spatial resolution. For

example, the interaction volume containing 90% of scattered electrons

is typically used as a reference in the AEM literature to determine the

resolution, although more stringent criteria [with 95% of the electrons

Chapter 4 Analytical Electron Microscopy 349

(Faulkner and Norrgard, 1978) and 99% of the electrons (Reed, 1966)]

have also been proposed. Although broadening values can be retrieved

from the simulated trajectories in a few minutes of computation even

on laptop computers or through web-based programs (Hovington

et al., 1997), quick estimates of the electron beam broadening are neces-

sary to evaluate the approximate loss of spatial resolution in micro-

analysis. Goldstein et al. (1977) developed a simple analytical model

assuming a single scattering event in the middle of the foil thickness

Figure 4–63. Simulation of the electron trajectories in a thin sample of Au

(100 nm thickness) using the Monte Carlo method for 100-keV incident elec-

trons. Calculations of electron trajectories are carried out using the public-

domain code CASINO developed in the Gauvin group (Hovington et al., 1997)

available on the web (http://www.montecarlomodeling.mcgill.ca).

Figure 4–64. Electron trajectories in a 100-nm-thick Au Monte Carlo calcula-

tions for 300-keV incident electrons.

350 G. Botton

(Figure 4–65) to calculate the broadening of the electron beam b that

contains 90% of the scattered electrons:

t=×

(

)

721 10

(55)

where b is the broadening in centimeters, Z is the atomic number, A is

the atomic weight, E

is the accelerating voltage (electronvolts), ρ is the

density (grams/cubic centimeter), and t is the specimen thickness (cen-

timeters). This simple equation is the most common method to esti-

mate the broadening and is most suitable for foils of thickness

approximately equal to the elastic mean free path (see Section 3.2),

although reﬁ nements were proposed to account for multiple scattering

in thicker foils (Cliff and Lorimer, 1981; Goldstein et al., 1986).

The spatial resolution can be determined based on the contribution

of both the electron beam size (d) and the electron beam broadening

(b). Early models proposed the addition of the two terms in

quadrature

R = (b

+ d

)

1/2

(56)

to yield the resolution R, but the currently adopted deﬁ nition is based

on experimental evidence suggesting the use of a less stringent, but

still arbitrary, average sum of the two terms leading to a deﬁ nition of

spatial resolution based on the broadening in the middle of the foil

thickness as suggested in Figure 4–66:

Figure 4–65. Simpliﬁ ed diagram

describing the broadening of

electronic samples. The parameter

b describes the broadening at the

bottom of the foil using Eq. (55) and

the single scattering assumption.

Figure 4–66. Deﬁ nition of parameters related to the calculation of the resolu-

tion with Eqs. (57) and (56) [where R

max

is estimated with Eq. (56) as the

maximum broadening at the bottom of the foil] and R is the broadening in the

middle of the foil. d is the diameter of the incident electron beam.

Chapter 4 Analytical Electron Microscopy 351

max

(57)

where R

max

is determined from Eq. (56) as the maximum broadening

at the bottom of the foil. If 90% of the beam current distribution is

considered, the resolution becomes (Keast and Williams, 2000)

Rdbdb=++

(58)

Recent measurements with sample geometries that probe the elec-

tron beam broadening at the bottom of the foil have been published

and have led to the conclusion that although the single scattering

models predict the right beam broadening magnitude, these quantita-

tively overestimate the broadening observed experimentally (Nakata

et al., 2001). More accurate models (Keast and Williams, 2000; Doigt

and Flewitt, 1982) consider a Gaussian probe distribution of standard

deviation σ and hence a probe with an FWHM of 4.29σ propagating

the foil with a distribution accounting for beam spreading and the

incident probe distribution (Keast and Williams, 2000)

Ixyt

(

)

()

−+

()













πσ β σ β22

exp

(59)

where β = 500(4Z/E

)

(ρ/A) and i

is the incident beam current.

Using this more detailed electron distribution in the probe (as well

as more simple models) as it travels through the sample, Keast and

Williams (1999, 2000) determined the equilibrium segregation proﬁ le

in grain boundaries based on composition line scans and two-

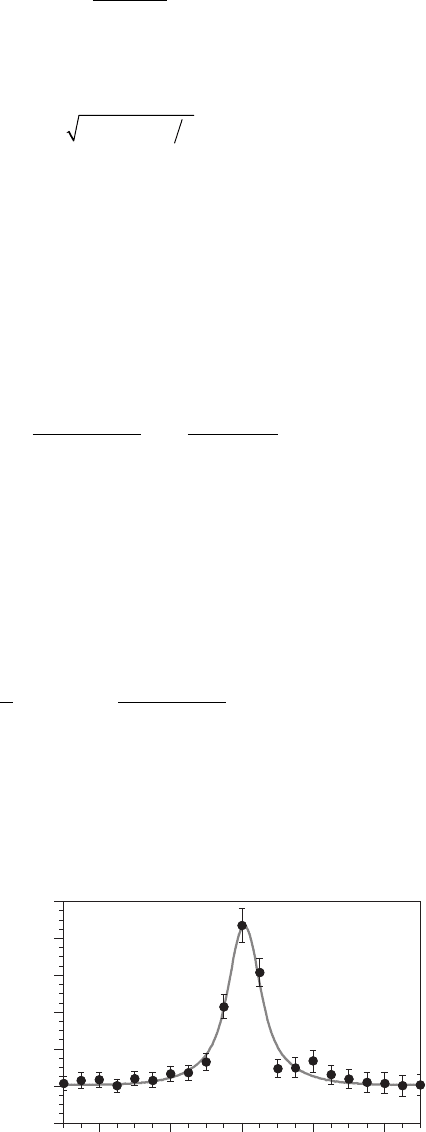
dimensional map measurements (Figure 4–67). Based on the Gaussian

intensity distribution of incident electrons the resolution, for a given

fraction of electrons Q, as a function of thickness, can be deﬁ ned as

=−

−

()

























∫

exp

σβ

(60)

where the integration is carried out over the thickness up to t = h where

R is the diameter of the cone deﬁ ning the resolution. The distribution

is assumed circularly symmetric (since there is no dependence of the

azimuth angle in the equation) and applicable to a two-dimensional

case. By deﬁ ning the resolution criteria based on the fraction of

-0.02

0.02

0.04

0.06

0.08

0.1

-4 -2 0 2 4

distance (nm)

S/Ni (counts)

Figure 4–67. Composi-

tion proﬁ le of S segrega-

tion at an Ni grain

boundary. The proﬁ le is

based on the modeling

of the beam proﬁ le

using a Gaussian

probe distribution and

Eq. (59) (Keast and

Williams, 2000). (Proﬁ le

courtesy of V. Keast,

University of Sydney.)

352 G. Botton

electrons within a given radius, it is possible to plot the expected reso-

lution (Figure 4–68) for a diameter containing 50% and 90% of elec-

trons. A comparison of the predictions with experimental proﬁ les

obtained on equilibrium segregation in Cu (for FWHM and at 10%

maximum) (Keast and Williams, 2000) shows excellent agreement for

thicknesses up to the elastic mean free path.

With a dedicated STEM, recent work on grain boundary segregation

and multilayer composite materials has shown that it is possible to

detect submonolayer segregation at grain boundaries (Keast et al., 1998;

Keast and Williams, 1999, 2000) and map the composition of quantum

wells in semiconductor materials (Figure 4–69). EDXS analysis with

Figure 4–68. Resolution

variation as a function of

thickness for the 50% and 90%

fraction of electrons within

the beam. (Adapted from

Keast and Williams, 2000.)

Figure 4–69. Quantita-

tive EDXS elemental

maps of In-rich quantum

wells in semiconductors

and related intensity

proﬁ les across the

quantum wells. (Cour-

tesy of V. Keast, Univer-

sity of Sydney.)

Chapter 4 Analytical Electron Microscopy 353

aberration-corrected instruments has been recently reported by

Watanabe et al. (2005) and Watanabe and Williams (2005a).

5.2 Energy-Filtered Microscopy and EELS Microanalysis

The spatial resolution in energy loss spectroscopy measurements is

strongly dependent on the operating mode of the microscope during

EELS analysis due to the illumination conditions of the area of interest,

the effects of lens aberration, and the spectrometer coupling condi-

tions. The contribution from the microscope lens aberrations comes

essentially from the objective lens and can be calculated as follows.

With respect to an incident beam of primary energy E

propagating

along the optic axis, the inelastic interactions that induce an energy

loss E and scattering at an angle θ will cause a blur of an object point

(and the image on the viewing screen of the microscope) due to chro-

matic aberrations R = M

θ∆f where M

is the magniﬁ cation of the objec-

tive lens and ∆f = C

(E/E

). According to the Rayleigh criterion, two

object points with blurred independent distributions can be resolved

if they are separated by a distance giving rise to an intensity drop of

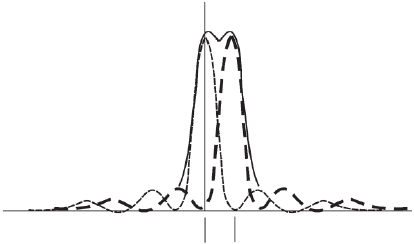
20% between the maxima of the summed distributions (Figure 4–70).

The distance between these two points is deﬁ ned as the resolution

and is obtained as (Egerton, 1996)

≈ 2θ

∆f ≈ C

(E/E

)

(61)

This resolution is expected for energy-ﬁ ltered images acquired at an

energy loss E when the incident electron energy is kept constant, the

image is initially focused for electrons that have lost no energy (which

is also known as a zero-loss image, Section 2.4.1), and the scattering

angles are limited only by the intrinsic scattering distribution at the

energy loss E (i.e., no limiting objective aperture is used). For images

of thick samples, it should be pointed out that the inelastic losses can

constitute the most important part of the signal resulting in signiﬁ cant

blurring of images. These contributions can be removed by energy ﬁ l-

tering so that the inelastically scattered electrons are removed with the

Figure 4–70. Rayleigh deﬁ nition of resolution based on the overlap of two

diffracting-limited functions placed in close proximity to each other. If the

sum of the two intensity proﬁ les shows a dip of 20% of the maximum intensity,

the peaks are considered to be resolvable.

354 G. Botton

energy-selecting slit and the images appear sharp even for thick samples

(Figure 4–71). In typical conditions for optimum energy loss imaging

at an energy loss E, however, the incident electron energy is readjusted

so that the spectrometer is focused at the energy loss E (i.e., by raising

the high tension of the microscope so that the primary energy is now

+ E) and the electrons of the related loss are in focus. If an energy-

selecting slit ∆E wide is used, the resolution becomes (Egerton, 1996)

≈ 2θ

∆f ≈ (C

/4)(∆E/E

)

(62)

When the angular distribution of scattering is limited by an objective

aperture β smaller than the angular distribution of scattering, namely

, other contributions become dominant (diffraction limit, spherical

aberration, delocalization of scattering) and the spatial resolution in

elemental maps is derived from a combination of all factors as described

in Section 6.2.3.

For point analyses carried out in TEM image mode, the spectrometer

entrance aperture is used to select electrons from the regions of interest

so that they enter the spectrometer for analysis. In these conditions,

the chromatic aberration will also cause contributions from areas

further away from the spectrometer aperture-delimited area due to the

signiﬁ cant broadening of the angular distributions and high energy

losses. If no angular-selecting aperture (the objective aperture in this

case) is used, the total broadening due to angular scattering up to the

Bethe-ridge (θ

= θ

, which includes most of the scattering intensity, see

Section 3.4.1) is

≈ θ

∆f (63)

while the use of an angular-selecting aperture (in the objective back-

focal plane when the TEM is operated in image mode) will limit the

a) b)

Figure 4–71. (a) Energy-ﬁ ltered image of an Al alloy with strengthening

precipitates. The image has been obtained by selecting only the electrons

that have not lost signiﬁ cant amounts of energy (i.e., zero-loss image) and (b)

unﬁ ltered image (containing all the inelastically scattered electrons). Although

the total intensity is reduced, the precipitates are more clearly deﬁ ned with

sharper edges in the zero-loss image.