Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 4 Analytical Electron Microscopy 315

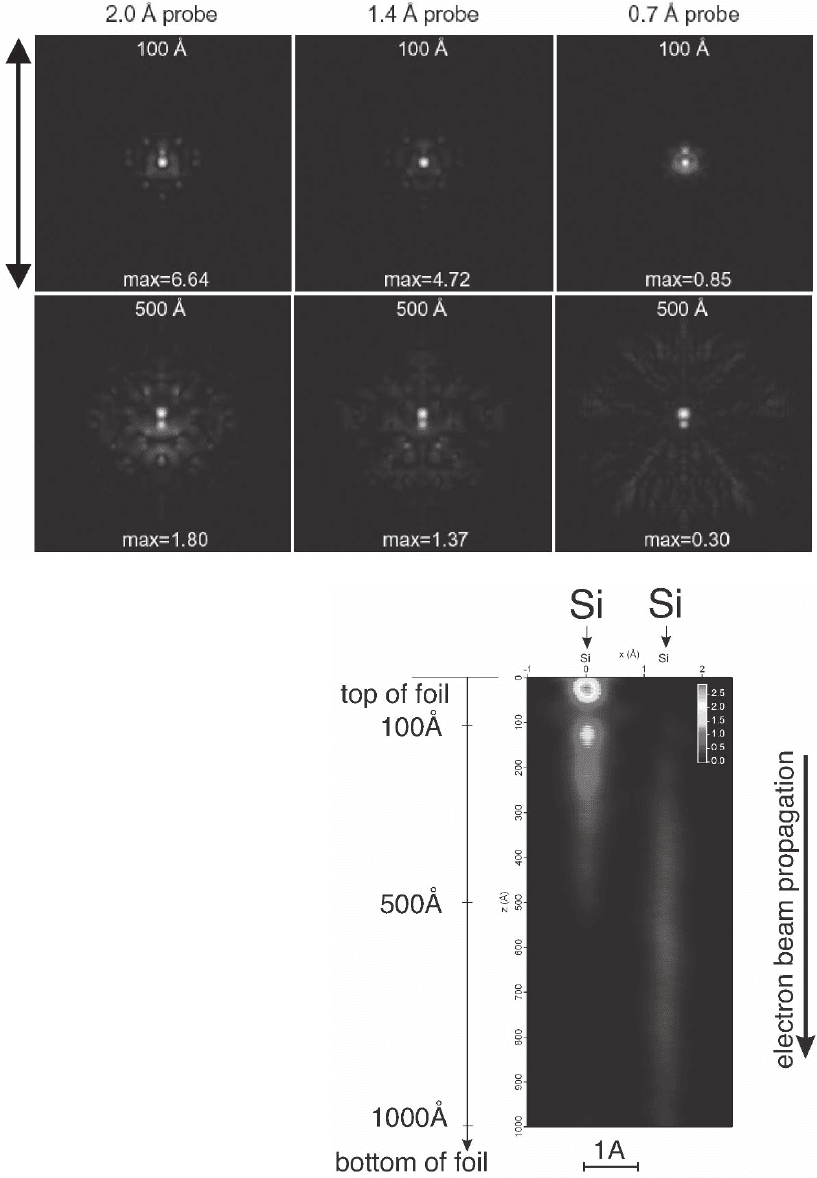
Figure 4–36. Real space intensity dis-

tribution of the probe electron density

in the sample as it propagates through

the thickness of the foil. Plots of the

intensity distribution at two depths

(100 and 500 Å) are shown for incident

probe sizes of 2, 1.4, and 0.7 Å (as

obtained with an aberration-corrected

microscope) when the electron beam is

positioned on the atomic column down

the 110 orientation of the crystal (arrow

length is 16.3 Å). The electron beam is

channeled onto the atomic column, but

the intensity maxima moves from one

atomic column to the adjacent one

(Dwyer and Etheridge, 2003). (Images

courtesy of C. Dwyer and J. Etheridge.)

(b) Alternate visualization of the

process of channeling viewed as a

function of thickness. The beam inten-

sity clearly channels from one atomic

column to the adjacent one as the

electrons propagate in the sample

with permission from Cambridge

University Press.)

316 G. Botton

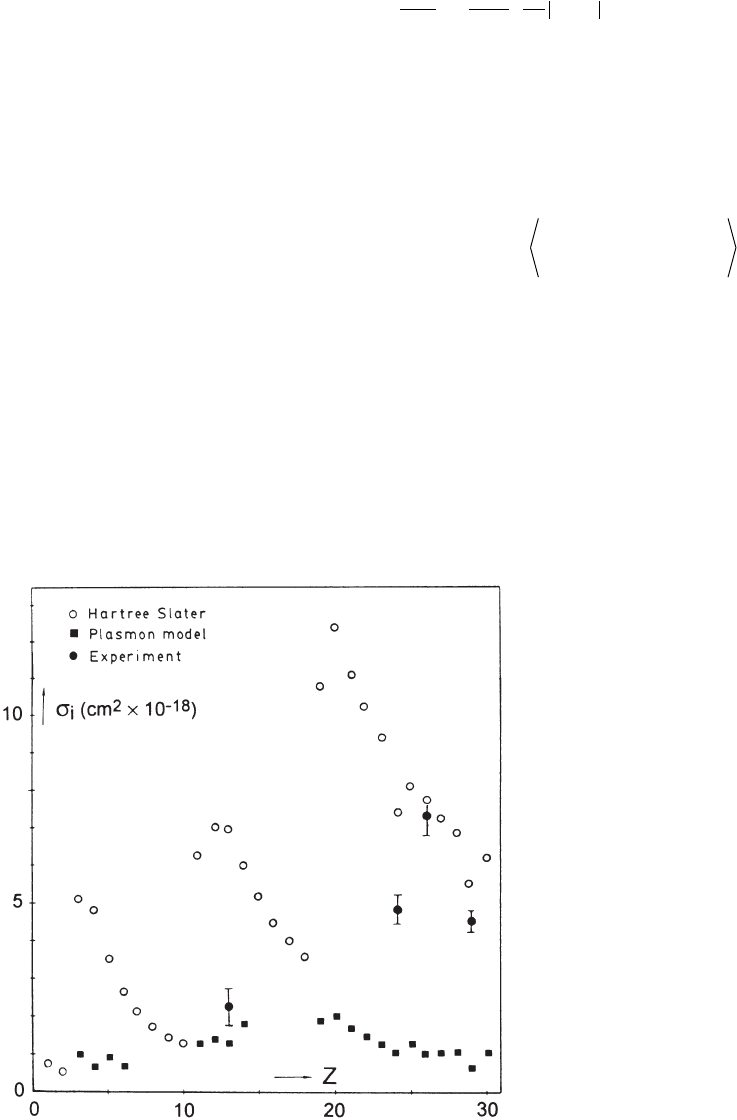
total inelastic and elastic scattering cross sections make it possible to

compare the width of the respective angular distributions. The angular

distributions are Lorentzian with an angular width of θ

for the inelas-

tic distributions and θ

for the elastic distribution. It is also possible to

note that the angular width of the elastic distribution (for scattering

from free atoms) is larger than the inelastic distribution.

max = 0.02min = 0.00

0.7

probe OFF columns

300

0.7 Å probe ON column

16.3

max = 0.36min = 0.00

300 Å

a) b)

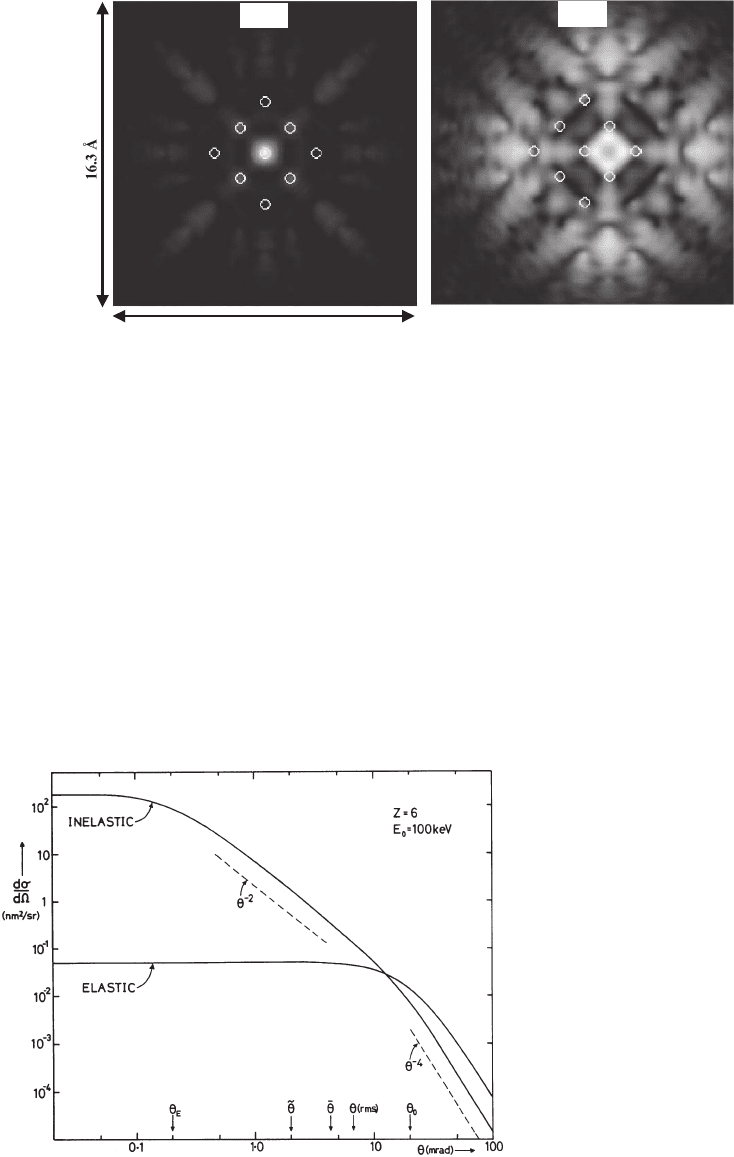
Figure 4–37. Real space intensity plots demonstrating the dispersion of the electron intensity when

the electron beam is located on top of the atomic column and when it is located between two atomic

columns. The bright empty circles indicate the position of the atoms in the cell closest to the point of

impact of the electron beam. Channeling is observed when the beam is positioned on the atomic

column (a) while much stronger dispersion is observed when the electron beam is not on the atomic

column (b). (Data courtesy of C. Dywer and J. Etheridge.) (For part A, see color plate.)

Figure 4–38. Comparison of the

elastic and total inelastic angular

scattering distributions for the C

atoms at 100 keV. The characteristic

angles for the inelastic and elastic

distributions (θ

and θ

), the mean

angle θ

, the median angle θ

, and the

root-mean-square angle θ

rms

are

permission from Springer Science+

Business Media.)

Chapter 4 Analytical Electron Microscopy 317

The total cross section integrated up to a scattering angle β is

relevant when calculating the inelastic free path or the stopping power

(see below)

σβ

πγ

βθθθ

θβ θ θ

()













(16)

The total inelastic scattering cross section integrated over all scattering

angles is approximated by

≈ 16πγ

1/3

ln (θ

/θ

) ≈ 8πγ

1/3

ln (2/θ

) (17)

by replacing the cutoff angle θ

with the Bethe-ridge angle (2θ

)

1/2

. This

expression leads to a comparison of the relative magnitude of the

elastic and inelastic cross sections as described by

/σ

≈ 2 ln (2/θ

)/Z = C/Z (18)

where the coefﬁ cient C (around 20) does not vary signiﬁ cantly with

atomic number and incident electron energy.

This expression can be used to calculate the scattering contrast as

deﬁ ned in Reimer (1995) and to interpret the contrast in STEM images

obtained by calculating the ratio of inelastic and elastic signals.

These calculations are a good ﬁ rst approximation of the behavior of

the inelastic cross sections with further reﬁ nements, accounting for the

outer-shell electrons, leading to systematic variations in the total cross

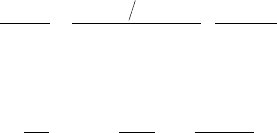
sections related to the ﬁ lling of the periodic table. Minima in the inelas-

tic cross sections occur for atoms with closed shell while maxima occur

for atoms ﬁ lling the s shell due to strong effects of valence excitations

(Egerton, 1996) (Figure 4–39).

The importance of the total inelastic cross section becomes apparent

in AEM as it forms the basis of calculations of the stopping power of

the electrons in the solid. This quantity is therefore relevant to under-

standing the propagation of the electrons and simulation of electron

trajectories in Monte Carlo simulations (Section 5.1):

nE==

(19)

where E is the energy loss, z is the distance traveled in the sample, E

–

the mean energy loss for the inelastic event, and n

is the number of

atoms in the solid per unit volume.

The total inelastic cross section considers all possible events giving

rise to energy losses represented by an average energy loss E

–

and does

not consider the individual interactions of the incident electrons with

the inner shells or outer shell atomic electrons. Predictions of the details

of a spectrum and the intensity at a given energy loss, however, must

take into account these various inelastic processes, their energy depen-

dence, and the angular distribution of scattering. To do so, we must

consider Bethe’s theory to predict the probability of transitions of elec-

trons from an initial state wavefunction ψ

to ﬁ nal state wavefunction

following interaction with incident fast electrons and the related

cross section. If the energy losses and the momentum transfer are

small compared to the momentum of the incident electron and there

318 G. Botton

is only one scattering event during the interaction (the ﬁ rst Born

approximation) the cross section can be described by

σγ

Ω













(

)

(20)

where k

and k

are the magnitudes of the wave vectors of the incident

electron before and after scattering respectively and q is the scattering

vector related to the momentum transfer h

q = h

− k

) (Figure 4–40).

The ﬁ rst term has already been encountered in the description of

Rutherford scattering for a single charge [Eq. (8)] and constitutes the

amplitude factor in the cross section. This term is modiﬁ ed by the inelas-

tic form factor related to the transition matrix element deﬁ ned as

ετ

id i=⋅

(

)

=⋅

(

)

∫

∑∑

ΨΨΨ Ψ

exp | exp |qr qr

00 0

(21)

which expresses the interaction of the incident electron and the atomic

electron via an operator exp(iq ⋅ r

) where r

is the coordinate position

of the fast electron treated as a plane wave and the sum is carried out

over the atomic electrons from j = 1 to j = Z. This form factor contains

the information related to the properties of the material through the

wavefunctions of the electrons in the solid (see Section 8.1). |ε

(q)|

independent of the electron energy and solely dependent of the atom

and its environment.

From the form factor, the generalized oscillator strength (GOS) can

be deﬁ ned as

Figure 4–39. Total inelastic cross

sections as a function of atomic

number (80 keV electrons). Open

circles are calculations based on the

Hartree–Slater models, solid squares

are based on calculations accounting

for plasmon losses, and the solid

circles are experimental data. (From

from Springer Science+Business

Media.)

Chapter 4 Analytical Electron Microscopy 319

(

)

(

)

(

)

(22)

where R is the Rydberg energy (13.6 eV) and E

is the energy loss of the

transition. This term contains also information on the probability of

the transition from an initial state wavefunction ψ

to a ﬁ nal state

wavefunction ψ

Using the concept of the generalized oscillator strength, the cross

section can be expressed as

σγ

Ω

(

)

(23)

The full angular and energy dependence of the scattering can be

described by the double differential cross section

ddE

4σγ

Ω

(

)

(24)

where the scattering vector q is expressed in term of scattering angle

θ (Figure 4–40) and the initial and ﬁ nal wavevectors k

and k

. For

small scattering angles and small energy losses relative to the incident

energy (as in typical TEM experiments) k

≈ 1 and

≅ k

(θ

+ θ

) (25)

with θ

the relativistically corrected characteristic scattering angle

()

(

)













Emcvc

Emc

(26)

and the cross section becomes

ddE

Em v

222

1σγ

θθ θθ

Ω

≈

























ddf

(27)

Figure 4–40. Inelastic

scattering diagram

showing the scattering

vectors, the energy loss,

and the effect of the

classical impact param-

eter b on the scattering

angle (also refer to dis-

cussions on spatial res-

olution in Section 6).

320 G. Botton

The ﬁ rst two terms of Eq. (27) represent a kinematic term of the scat-

tering while the df/dE term provides the information on the initial and

ﬁ nal wavefunctions of the electrons (including changes in the bonding

state) either via inner shell or valence excitations. The second term

imposes a Lorentzian angular distribution of scattering at small scat-

tering angles as it contains the term θ

representing the half-width of

the distribution. At low energy losses and small scattering angles (i.e.,

q → 0), df/dE does not vary with θ and it can therefore be considered

as a dipole oscillator strength. In this region of scattering (achieved by

limiting the maximum scattering angle θ with a small aperture β) the

response to the excitation from an electron would be equivalent to the

excitation by a photon.

3.3.1 Outer Shell Excitations

The expression of df/dE has been derived in Bethe’s theory using atomic

models. To treat inner shell excitations, the initial and ﬁ nal wavefunc-

tions of the electrons must be known. These wavefunctions vary with

the chemical state in a solid but the atomic models are still a good

approximation for the purpose of quantiﬁ cation of the atomic concen-

tration based on intensity of edges. In the case of a solid, however,

wavefunctions related to outer shell excitations are much more strongly

modiﬁ ed by the interaction between atoms and the collective behavior

of the electrons. Similarly, to model ﬁ ne modulations in the edges

simple atomic models are not sufﬁ cient (Section 8.1). To consider these

effects it is more convenient to consider the dielectric response of the

medium ε(q,E) to the incident electron treated as a point charge per-

turbing the solid.

The dielectric formulation of scattering relates the double differen-

tial scattering cross section to

ddE

amvn

222

1σ

πθθ

Ω

≈

−

(

)

[]













Im ,

(28)

thus the GOS relates to the dielectric function as

(

)

−

(

)













(29)

where E

= h

/(ε

), n

is the number of electrons per unit volume,

and Im[−1/ε(q,E)] is the loss function that contains all the material

dependence via the complex dielectric response of the solid ε = ε

+ iε

to electromagnetic radiation. The real part of the dielectric function

Re[ε(q,E) − 1] = ε

(q,E) − 1 is related to the polarizability of the medium

and the imaginary part Im[ε(q,E)] = ε

is related to the absorption.

Maxima in the loss function Im(−1/ε) = ε

/(ε

+ ε

) that result in strong

peaks in the energy loss spectra (Figure 4–7) occur when ε

= 0 and ε

is small (the damping is weak). The condition ε

= 0 suggests that a

condition of resonance is met and that the medium in unstable. This

instability corresponds to creation of a quasiparticle called plasmon of

energy E

. Further discussion on the derivation of the loss function and

applications can be found in Section 8.2.

Chapter 4 Analytical Electron Microscopy 321

3.4 Calculations of Cross Sections

Quantiﬁ cation of EELS and EDXS spectra based on signals recorded

from edges and X-ray peaks (Section 4) is based on the knowledge of

cross sections. For inner shell excitations in EELS (and the related EDXS

peaks) it is assumed, as a ﬁ rst approximation, that the initial and ﬁ nal

wavefunctions are not affected by collective electron behavior and the

cross sections can be calculated using various models based either on

the simple hydrogenic description of the atomic electrons or the more

accurate Hartree–Slater method. For an atom of atomic number Z, the

hydrogenic model uses the simpliﬁ cation of the electrostatic potential

arising from the treatment of the nuclear charge Ze and the screening

due to remaining inner nonexcited electrons. Different expressions of

the effective charges are used for K and L shells and consideration is

given to the presence of outer electrons in higher energy levels that

modify the binding energy of the inner shell electrons. Solving the

Schrödinger equation in the revised simpliﬁ ed potential leads to ana-

lytical solutions that can be easily calculated for K shells using pro-

grams developed by Egerton (1996). The treatment of L shells, although

initially unsuccessful due to the simpliﬁ cations of the hydrogenic

model, was revised by considering experimental optical and energy

loss data with built-in corrections. These modiﬁ cations have led to

improved accuracy in the treatment of L shells for transition metals;

programs and models for L shells are also available (Egerton, 1996) in

the literature and in commercial EELS analysis programs (the Digital

Micrograph software from Gatan). Empirical modiﬁ cations of the

hydrogenic models for M edges have also been developed (Luo &

Zeitler, 1991). The Hartree–Slater (HS) approach requires iterative solu-

tions that lead to more accurate cross sections that consider a potential

calculated based on the charge density of the electrons in a self-

consistent manner. Cross section tabulations have been developed by

Leapman et al. (1980) and Rez (1982) and the results have been imple-

mented within commercial EELS analysis software for K, L, and M

shells within Digital Micrograph. The HS model predicts more realistic

shapes of edges and includes corrections for sharp features related to

unoccupied bound states present on transition metal L edges. Recent

developments allow the combination of solid-state effects near the edge

threshold, calculated from band structure techniques, with the atomic

models at higher energy losses into more accurate cross section models

(Potapov et al., 2004).

3.4.1 Angular and Energy Dependence of the GOS

Some physical insight into the scattering process is given by the analy-

sis of the angular and energy dependence of the GOS df(q,E)/dE, known

as the Bethe surface, as plotted for the C K edge (Figure 4–41a). This

plot also provides information related to the optimization of the acqui-

sition conditions as it shows the dependence of the differential cross

section on angle and energy loss. There are two regions of key impor-

tance on the Bethe surface. At energy losses just above the threshold,

the distribution is peaked at small scattering angles (θ = 0, q → 0) and

the angular dependence in the cross section d

σ/dΩdE is controlled by

322 G. Botton

Figure 4–41. (a) Two-dimensional angular and energy distribution of the general oscillator strength

per unit energy loss (df/dE) for the CK edge (also described as the Bethe surface of scattering). The

“hump” at high energy from the edge onset and large scattering vector q is the Bethe ridge. (From

matic plot of the full energy and scattering angle distribution of inelastic losses including plasmon

losses, core losses, as well as the Bethe ridge and the plasmon dispersions. The diagram shows the

elastic scattering as part of Bragg peaks (as in a crystalline sample). Scattering from atoms or amor-

phous samples would give rise to a broad peak centered at zero scattering angle. The angle (β) and

energy (∆) integration windows for the calculations of the partial cross sections are identiﬁ ed. (Adapted

from Schattschneider and Werner, 2005.)

Chapter 4 Analytical Electron Microscopy 323

the kinematic term of the cross section since the GOS does not vary

strongly with q at small scattering angles. This region of the GOS is

known as the dipole region and represents collisions with a large

impact parameter b (see Figure 4–40 and Section 5.2) and little momen-

tum transfer. Spectra acquired with small scattering angles in electron

energy loss experiments are thus equivalent to optical (X-ray) absorp-

tion spectra where only dipole transitions are allowed. Based on this

equivalence, photoabsorption spectra can be used to improve GOS

models for use in cross-sectional calculations (Egerton & Leapman,

1995; Egerton, 1993). The dipole transitions also imply that the change

of angular momentum quantum number 艎 when the electron is ini-

tially excited from a core level “i” to a ﬁ nal level “f” is ∆艎 = ±1.

At larger energy losses from threshold, corresponding to collision

with nearly-free electrons, the GOS peaks at large scattering angles θ

= (E/E

)

corresponding to what is known as the Bethe ridge. Experi-

mentally, this peak can be readily visualized by collecting energy loss

spectra in thin samples with a spectrometer aperture centered few tens

mrad off the transmitted beam collection angle (thus away from the

forward scattered direction). This acquisition condition is equivalent

to Compton scattering experiments between an incident electron

and a free electron. As discussed in a review by Schattschneider and

Exner (1995), a quantitative analysis of the width of this experimental

peak provides information on the momentum distribution of atomic

electrons. Similarly, by recording diffraction patterns of thin speci-

mens with an energy ﬁ lter (see Section 2.4.1) at high energy loss (few

hundred electronvolts) it is possible to see a ring corresponding to the

Compton scattering peak (Mayer et al., 1995; Egerton, 1996). The full

energy and scattering angle dependence of the entire spectrum includes

therefore the various processes of low-loss scattering (including the

dispersion of plasmon losses, the elastic Bragg scattering (in crystalline

specimens) and the core losses (with the Bethe ridge visible) (Figure

4–41b).

3.4.2 Partial and Total Ionization Cross Sections

Whether we have to compute cross sections for quantiﬁ cation of EDXS

or energy loss spectra, the differential cross sections have to be inte-

grated with respect to angle and energy loss to yield partial or total

cross sections. In the case of energy loss experiments, the spectra are

recorded with a ﬁ xed collection angle β and the partial cross section

is therefore related to the double differential cross section through

integration up to an angle β

Em v

df q E

θθ

≅

(

)

()

∫



(30)

where the GOS is expressed in terms of the scattering vector q and the

scattering angle is θ. By considering the kinematics of scattering (Figure

4–40), q

≅ k

(θ

+ θ

) and the integration can be either carried out over

θ or, after transformation of variables and limits of integration, over q

(Egerton, 1996). The partial cross section follows a simple trend as dσ/

dE ⬀ E

−s

where s is the slope of the function.

324 G. Botton

For the purpose of quantiﬁ cation in energy loss spectroscopy (see

Section 4.2), core shell edge spectra acquired with a collection angle β

are integrated over an energy window ∆. The integrated signal for a

given collection angle β and energy window is thus related to the

partial cross section as

(β,∆) = NI

(β,∆) (31)

where N is the number of atoms per unit area, I

is the incident intensity

(approximated by the number of counts under the zero-loss peak), and

σβ

, ∆

∆

(

)

∫

(32)

Examples of the values of partial cross section for light elements as

a function of collection angle β are shown in Figure 4–42. These plots

Figure 4–42. Angular dependence of the partial cross sections for lighter

elements. The energy integration is carried out over an energy window ∆

equivalent to 0.2 E

where E

with permission from Springer Science+Business Media.)