Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

1242 S. Van Aert et al.

from the parametric model. This estimator is important since it achieves

the CRLB asymptotically. In Section 5.4, an important purpose for

which the expressions for the CRLB can be used will be introduced,

namely, statistical experimental design.

5.1 Parametric Statistical Models of Observations

Generally, due to the inevitable presence of noise, sets of observations

made under the same conditions nevertheless differ from experiment

to experiment. The usual way to describe this behavior is to model the

observations as stochastic variables. The reason is that there is no viable

alternative and that it has been found to work (van den Bos, 1999; van

den Bos and den Dekker, 2001). By deﬁ nition, a stochastic variable is

characterized by its probability density function, while a set of stochas-

tic variables has a joint probability density function.

Consider a set of stochastic observations w

, m = 1, . . . , M made at

the measurement points x

, . . . , x

. These measurement points are

assumed to be exactly known. In electron microscopy, the observations

are, for example, electron counting results made at the pixels of a CCD

camera, where M represents the total number of pixels. The reader

should not be misled by the fact that the observations and measure-

ment points are here represented in a one-dimensional way. It is

intended as a general representation. Also if the observations and

measurement points would be two- or higher-dimensional, they can

easily be transformed to a one-dimensional representation. For example,

if the observations and measurement points are two-dimensional, say,

, k = 1, . . . , K, l = 1, . . . , L and x

, k = 1, . . . , K, l = 1, . . . , L, respec-

tively, they can also be represented as w

, m = 1, . . . , M and x

, m =

1, . . . , M, respectively, with M = K × L. The M × 1 vector w deﬁ ned as

w = (w

. . . w

)

(16)

is the column vector of these observations. It represents a point in the

Euclidean M space having w

, . . . , w

as coordinates. This will be

called space of observations (van den Bos and den Dekker, 2001). The

expectations of the observations, that is, the mean values of the obser-

vations, are deﬁ ned by their probability density function. The vector

of expectations

E[w] = (E[w

] . . . E[w

])

(17)

is also a point in the space of observations and the observations are

distributed about this point. The symbol E[⋅] denotes the expectation

operator. The expectations of the observations are described by the

expectation model, that is, a physical model, that contains the unknown

parameters to be estimated, such as the position coordinates of the

projected atoms or atom columns. In a sense, this model has ﬁ rst been

introduced in Section 4 on the understanding that it now describes the

expectations of the observations whereas in Section 4, the model

describes noise-free observations. The unknown parameters are

represented by the R × 1 parameter vector τ = (τ

. . . τ

)

. Thus, it is

supposed that the expectation of the mth observation is described by

Chapter 20 The Notion of Resolution 1243

E[w

] = f

(τ) = f(x

; τ) (18)

where f

(τ) represents the expectation model, which is evaluated at the

measurement point x

and which depends on the parameter vector τ.

Apart from the unknown parameters τ, the expectation model may

contain known parameters and experimental settings as well. An

example of an expectation model is given by Eq. (10).

Electron microscopic observations are electron counting results

detected, for example, with a CCD camera. Under the assumption that

the quantum efﬁ ciency of this detector is sufﬁ ciently large to detect

single electrons, these observations may be assumed to be Poisson

distributed. This means that the probability that the observation w

equal to ω

is given by (Papoulis, 1965)

exp −

(

)

(19)

where the parameter λ

is equal to the expectation of the observation

, which, in its turn, is described by the expectation model.

Therefore,

E[w

] = λ

= f

(τ) (20)

with f

(τ) given by Eq. (18). A property of the Poisson distribution is

that the variance of the observation w

is equal to λ

var(w

) = λ

(21)

Moreover, electron microscopic observations may be assumed to be

statistically independent. The probability P(ω; τ) that a set of observa-

tions w = (w

. . . w

)

is equal to ω = (ω

. . . ω

)

is thus equal to the

product of all probabilities described by Eq. (19):

ωτ

;

exp

(

)

=−

(

)

∏

(22)

This function is called the joint probability density function of the obser-

vations. It represents the parametric statistical model of the observa-

tions. The parameters τ to be estimated enter P(ω; τ) via λ

If the expectation E[w

] = λ

increases, the Poisson distribution tends

to a normal distribution with both expectation E[w

] and variance

var(w

) equal to λ

of the Poisson distribution (Mood et al., 1974). This

normal approximation is justiﬁ ed if the magnitude of the observations

is large with respect to the square root of this number (Koster

et al., 1987). Moreover, if the contrast in the images is low, the devia-

tions of the observations from their expectations may be supposed to

be identically distributed, that is, var(w

) = σ

(Miedema et al., 1994).

Under these conditions the joint probability density function of the

observations is given by

ωτ

πσ

ωλ

;exp

(

)

=−

−





















∏

(23)

1244 S. Van Aert et al.

In Section 5.2, the parameterized joint probability density function

will be used to derive the CRLB, that is, an expression for the attainable

precision with which the unknown parameters can be estimated unbi-

asedly from the observations. In Section 5.3, from the joint probability

density function, the ML estimator of the parameters will be derived.

This estimator actually achieves the CRLB asymptotically, that is, for

the number of observations going to inﬁ nity.

5.2 The Cramér–Rao Lower Bound

In this section, the parameterized probability density function of the

observations, which is derived in Section 5.1, will be used to deﬁ ne the

Fisher information matrix and to compute the CRLB on the variance of

unbiased estimators of the parameters of the expectation model. The

CRLB will also be extended to include unbiased estimators of vectors

of functions of these parameters. As discussed in the introduction of

Section 5, the CRLB is used as a criterion for statistical model-based

resolution. The reader is referred to van den Bos (1982), Frieden (1998),

and van den Bos and den Dekker (2001) for the details of the CRLB.

First, the Fisher information matrix F with respect to the elements of

the R × 1 parameter vector τ = (τ

. . . τ

)

is introduced. It is deﬁ ned as

the R × R matrix

=−

∂

(

)

∂∂













ln ;w

ττ

(24)

where P(ω; τ) is the joint probability density function of the observa-

tions w = (w

. . . w

)

. The expression between square brackets repre-

sents the Hessian matrix of ln P, for which the (r, s)th element is deﬁ ned

by ∂

ln P(ω; τ)/∂τ

∂τ

. For electron microscopic observations, where

P(ω; τ) is given by Eq. (22), it follows from Eqs. (20), (22), and (24) that

the (r, s)th element of F is equal to

∂

∑

(25)

Furthermore, if the approximation of Eq. (22) by Eq. (23) is justiﬁ ed,

the (r, s)th element of F is equal to

∂

∑

(26)

Next, it can be shown that the covariance matrix cov(

τ) of any unbi-

ased estimator

τ of τ satisﬁ es

cov(

τ) ≥ F

−1

(27)

This inequality indicates that the difference of the matrices cov(

τ) and

−1

is positive semideﬁ nite. Since the diagonal elements of cov(

τ) rep-

resent the variances of

, . . . ,

and since the diagonal elements of a

positive semideﬁ nite matrix are nonnegative, these variances are larger

than or equal to the corresponding diagonal elements of F

−1

Chapter 20 The Notion of Resolution 1245

var(τ

) ≥ [F

−1

]

(28)

where r = 1, . . . , R and [F

−1

]

is the (r, r)th element of the inverse of the

Fisher information matrix. In this sense, F

−1

represents a lower bound

to the variances of all unbiased

τ. The matrix F

−1

is called the CRLB on

the variance of

τ.

The CRLB can be extended to include unbiased estimators of vectors

of functions of the parameters instead of the parameters proper. Let

γ(τ) = [γ

(τ) . . . γ

(τ)]

be such a vector and let γ

be an unbiased estimator

of γ(τ). Then, it can be shown that

cov

(

)

≥

∂

−

(29)

where ∂γ/∂τ

is the C × R Jacobian matrix deﬁ ned by its (r, s)th element

∂γ

/∂τ

(van den Bos, 1982). The right-hand member of this inequality

is the CRLB on the variance of γ

It should be noted that the CRLB may be computed only if the

probability density function of the observations is known. At ﬁ rst

sight, this seems to be a problem since the true parameters of the

probability density function are unknown. Nevertheless, even if the

CRLB is a function of the unknown parameters, it remains an

extremely useful tool. For nominal values of the unknown parameters

it enables one to quantify variances that might be achieved, to detect

possibly strong covariances between parameter estimates, and, as

will be shown in Section 5.4, to optimize the experimental design (van

den Bos, 1982). Moreover, the estimates obtained using an estimator

that achieves the CRLB may be substituted for the true parameters

in the expression for the CRLB so as to obtain a level of conﬁ dence

to be attached to these estimates (den Dekker and Van Aert, 2002;

den Dekker et al., 2005; Van Aert et al., 2005). This will brieﬂ y be

discussed in Section 5.3.

The attainable precision with which position and distance parameters

of one or two point objects can be measured has been investigated. The

observations consist of counting results in a one- or two-dimensional

pixel array. The model describing the expectations of these observa-

tions has been assumed to consist of Gaussian peaks with unknown

position. Under this assumption, the CRLB, which usually has to be

calculated numerically, may be approximated by a simple rule in closed

analytical form. Although the expectation model of images obtained

in practice are generally of higher complexity than Gaussian peaks, the

rules are suitable to provide insight in the attainable precision of posi-

tion and distance parameters using quantitative atomic resolution

TEM. In Bettens et al. (1999) and Van Aert et al. (2002a), the details of

this study can be found. In the following examples, only the main

results will be presented.

Example 2 (Position Measurement) In this example, the attainable preci-

sion of the position measurement of one isolated point object will be considered.

If the point spread function is assumed to be Gaussian and deﬁ ned by Eq. (1)

and if the total number of imaging particles is N, the lower bound on the

1246 S. Van Aert et al.

standard deviation s

of the coordinates estimates of the position, that is, the

square root of the CRLB, is given by

≈

(30)

or, from Eq. (3)

≈

(31)

Thus, the precision with which the position can be determined is a function of

both the Rayleigh resolution ρ

and the number of imaging photons N. If N is large,

the precision can be orders of magnitude higher than the point resolution ρ

Example 3 (Distance Measurement) Here, the attainable precision of the

distance measurement of two neighboring point objects will be considered. If

the imaging is supposed to be linear, the image consists of the superposition of

the two corresponding point spread functions as simulated in Figures 20–6

and 20–7. The total number of imaging photons used in the simulation is equal

to 2 N. This means that in agreement with Figure 20–5, the number of photons

per peak is equal to N. The results are different for distances smaller than or

larger than ρ

/2 and may be summarized as follows.

• d > ρ

This is shown in Figure 20–6. Now, the distance d between the atoms is

larger than the half of the Rayleigh resolution. Then, the lower bound on

the standard deviation s

MIN

on the distance d is minimal, independent of d,

and given by

MIN

≈

(32)

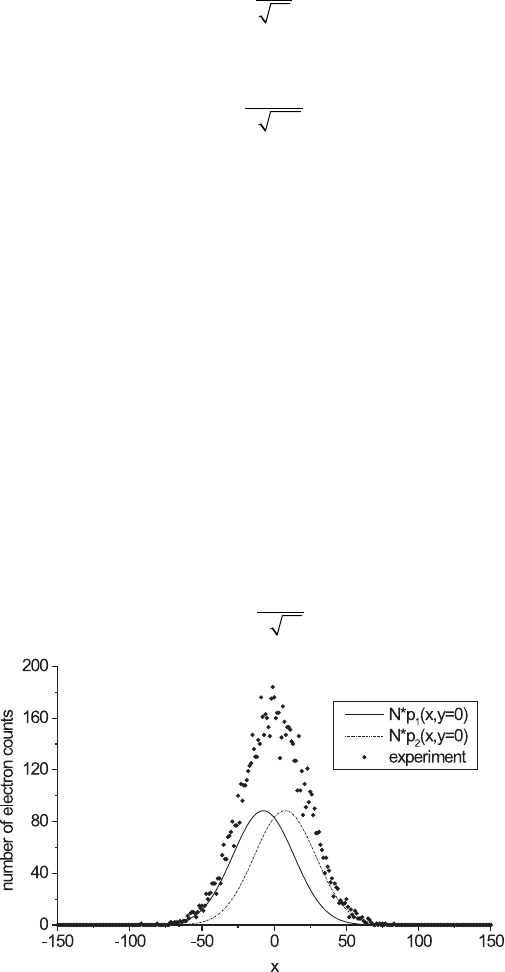
Figure 20–7. The results of a computer-simulated image of two neighboring

points with a Gaussian point spread function, where p

1,2

(x, y) are two-dimen-

sional normalized Gaussian point spread functions, as in Eq. (1). The experi-

mental as well as the expectation values of the individual peaks [N × p

1,2

(x, y)]

are plotted within the section y = 0. The number of imaging particles 2N is

equal to 500,000. The peaks overlap severely.

Chapter 20 The Notion of Resolution 1247

Thus, from Eq. (31) it follows that the CRLB on the variance of the distance

is twice the CRLB on the variance of the position of an isolated point

object:

MIN LB

2= (33)

The reason for this is that the coordinate estimates of neighboring atoms are

uncorrelated for distances larger than ρ

/2.

• d ≤ ρ

This is shown in Figure 20–7. Now, the distance d between the atoms is

smaller than the half of the Rayleigh resolution. Then, the lower bound on

the standard deviation s

increases inversely proportionally to the distance

d, following approximately the relation

MIN p

(

)

≈

(34)

where s

MIN

is given by Eq. (32).

In Figure 20–8, the lower bound on the standard deviation of the distance

d is shown as a function of the distance.

In this section, statistical model-based resolution has been discussed

in terms of the CRLB. In this discussion, the parametric statistical

model of the observations, that is, the joint probability density func-

tion, has been assumed to be exact. Then, it is clear that statistical

model-based resolution is limited by the lower bound on the variance

or on the standard deviation. This limit is fundamental. Moreover, if

the model is inaccurate, the introduced systematic error determines

another fundamental limit to statistical model-based resolution. Apart

from these fundamental limits, computational limits exist as well, just

as for deterministic model-based resolution. The computing time

needed to ﬁ t the model to the images with respect to the unknown

parameters increases with the total number of parameters to be

Figure 20–8. The lower bound on the standard deviation of the distance d as

a function of the distance.

1248 S. Van Aert et al.

measured. Furthermore, the optimization methods fail if the structure

is not resolved.

5.3 Maximum Likelihood Estimation

In this section, the derivation of the ML estimator of the parameters

from the parameterized probability density function, which is dis-

cussed in Section 5.1, will be discussed. This estimator is very impor-

tant since it achieves the CRLB asymptotically, that is, for the number

of observations going to inﬁ nity. Thus, it is asymptotically most precise

and is therefore often used in practice. The ML estimator is clearly

discussed in van den Bos and den Dekker (2001) and den Dekker et al.

(2005). A summary is given here.

The ML method for estimation of the parameters consists of three

steps:

1. The available observations w = (w

. . . w

)

are substituted for the

corresponding independent variables ω = (ω

. . . ω

)

in the probability

density function, for example, in Eq. (22) or in Eq. (23). Since the obser-

vations are numbers, the resulting expression depends only on the

elements of the parameter vector τ = (τ

. . . τ

)

2. The elements of τ = (τ

. . . τ

)

, which are the hypothetical true

parameters, are considered to be variables. To express this, they are

replaced by t = (t

. . . t

)

. The logarithm of the resulting function, ln

P(w; t), is called the log-likelihood function of the parameters t for the

observations w, which is denoted as q(w; t).

3. The ML estimates

of the parameters τ are deﬁ ned by the values

of the elements of t that maximize q(w; t), or

= arg max

q(w; t) (35)

For independent normally distributed observations with equal vari-

ance, for which the joint probability density function is given by Eq.

(23), it can easily be shown that the ML estimator is equal to the well-

known uniformly weighted least-squares estimator (van den Bos and den

Dekker, 2001; den Dekker et al., 2005). The uniformly weighted least-

squares estimates

of the unknown parameters τ are given by the

values of t that minimize the uniformly weighted least-squares criterion:

arg minτ

=−

(

)

[]

∑

tmm

wft

(36)

where the function f

is deﬁ ned by Eq. (18).

The most important properties of the ML estimator are the

following:

• Consistency. Generally, an estimator is said to be consistent if the

probability that an estimate deviates more than a speciﬁ ed amount

from the true value of the parameter can be made arbitrarily small

by increasing the number of observations used.

• Asymptotic normality. If the number of observations increases, the

probability density function of an ML estimator tends to a normal

distribution.

Chapter 20 The Notion of Resolution 1249

• Asymptotic efﬁ ciency. The asymptotic covariance matrix of an ML

estimator is equal to the CRLB. In this sense, the ML estimator is

most precise.

• Invariance property. The ML estimates γ

of a vector of functions of

the parameters τ, that is, γ(τ) = [γ

(τ) . . . γ

(τ)]

, are equal to γ(

) =

[γ

(

) . . . γ

(

)]

(Mood et al., 1974).

To evaluate the level of conﬁ dence to be attached to the obtained ML

estimates, conﬁ dence regions and intervals associated with these esti-

mates are required. A summary of existing methods to compute such

regions and intervals is presented in den Dekker et al. (2005). One of

these methods is based on the asymptotic normality of the ML estima-

tor. It is preferred, especially if the experiment cannot be replicated.

For example, an approximate 100(1 − α)% conﬁ dence interval for the

rth element of τ, τ

, is given by

τλ

αML

[]









−

(

)

−

(37)

with [

]

the rth element of the parameter vector

, [F

−1

]

the (r, r)th

element of F

−1

, and λ

(1−α/2)

the (1 − α/2) quantile of the standard normal

distribution. The meaning of a 100(1 − α)% conﬁ dence interval is that

it covers the true element τ

of τ with probability 1 − α. Usually, F

−1

a function of the parameters to be estimated. The conﬁ dence intervals

(37) are then derived by using approximations of F

−1

. A useful approxi-

mation

−1

of F

−1

may be obtained by substituting

for τ in the expres-

sion for the CRLB yielding

−1

= F

−1

τ=

(38)

The effectiveness of the ML method will be shown in the following

example, where it will be applied to experimental high-resolution TEM

(HRTEM) images of an aluminum crystal. The details of this study can

be found in Van Aert et al. (2005).

Example 4 (Maximum Likelihood Estimation of Structure Parame-

ters from HRTEM Images of an Aluminum Crystal) Structure param-

eters, atom column distances in particular, have been estimated from HRTEM

images of an aluminum crystal using the ML method. Therefore, 20 images

have been recorded and afterward been corrected for specimen drift using

cross-correlation. From these corrected images, a particular region consisting

of 51 times 50 pixels has been selected. The individual images resulting from

this procedure are shown in Figure 20–9. The observations corresponding to

these individual images, that is, the 51 times 50 image pixel values, are sup-

posed to be independent normally distributed with equal variance. For such

observations, the joint probability density function is given by Eq. (23).

Moreover, the expectation model has been supposed to be given by Eq. (10).

The unknown parameters of this model have then been estimated using the

ML estimator, which for these types of observations is equal to the uniformly

weighted least-squares estimator given by Eq. (36). Furthermore, ML esti-

mates of the atom column distances have been obtained using the invariance

property of the ML estimator. Also conﬁ dence intervals for the parameters

have been computed. For example, for the atom column distances, the

1250 S. Van Aert et al.

precision has been shown to be of the order of 0.03 Å, with the precision

represented by the square root of the approximated CRLB on the variance of

the distance with the approximated CRLB given by Eq. (38). Obviously, the

value to be attached to the obtained estimates and conﬁ dence intervals depends

on the validity of the model. Therefore, it is important to test the proposed

model before attaching conﬁ dence to these estimates. This has been done

using the model assessment methods described in den Dekker et al. (2005)

and Van Aert et al. (2005). From these methods, it could be concluded that

the proposed model is a sufﬁ ciently adequate description of the experimental

observations. The model evaluated at the obtained ML estimates is shown in

Figure 20–10. Note that this ﬁ gure may be regarded as an optimal image

reconstruction.

Figure 20–9. HRTEM

observations of an alu-

minum crystal.

Chapter 20 The Notion of Resolution 1251

Finally, the variation of the atom column distance estimates has been com-

pared to the variance that would be expected if the statistical ﬂ uctuations of

the observations would be the only source of variation of the distance esti-

mates. The former has been measured by means of the well-known sample

variance (Mood et al., 1974) and the latter by means of the CRLB. If statisti-

cal ﬂ uctuations would be the only source of contribution to the variation of

the distance estimates, the sample variance and the estimated CRLB should

be about equal to one another. However, from a comparison of both, it followed

that the sample variance was about 10 times larger than the estimated CRLB.

Hence, there must be a further, dominant contribution to the variation of

the distance estimates. Because of this the atom columns of the crystal were

not observed at a perfectly periodic crystal lattice in the experiment and, in

Figure 20–10. The exp-

ection models as des cr-

ibed by Eq. (10) evaluated

at the estim ated par-

ameters obta ined from

the experimental images

shown in Figure 20–9

using the ML method.