Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

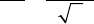
1232 S. Van Aert et al.

where g is the absolute value of the two-dimensional spatial frequency

vector g. Although this transfer function tends to zero for increasing

frequency values, it is not strictly band limited. Nevertheless, the

Gaussian approximation is sufﬁ ciently accurate for the purpose of this

chapter. From the condition that the product of the Rayleigh resolution

limit and the cutoff frequency should approximately be equal to one,

it follows from Eq. (3) that the cutoff frequency corresponding to

Rayleigh resolution is

=≈

(6)

At that spatial frequency the modulus of the transfer function, which

is given by Eq. (5), is reduced to only 8%. Thus, for Gaussian point

spread functions as described by Eq. (1), the Rayleigh resolution limit

can also be deﬁ ned as the inverse of the spatial frequency for which

the transfer function is reduced to 8% of its peak value.

The diffraction limit and its relation to Rayleigh and Sparrow resolu-

tion will now be discussed for conventional transmission electron

microscopy (TEM). Thus far, only the diffraction limited point spread

function of the imaging instrument has been taken into account.

However, for electron microscopy, this should be extended to include

the point spread function describing the effect of thermal vibrations of

the atom, the effect of the environment, and the detector (de Jong and

Dyck, 1993). Moreover, it has to be noted that the atoms are not point

scatterers. Hence, an extension from points to objects of ﬁ nite size has

to be made. As shown in Figure 20–1, each effect contributing to the

imaging process can be represented by a transfer function, which acts

as a low pass ﬁ lter. The transfer function of the electron microscope

consists of a damping function, which is mainly due to chromatic aber-

ration, and a phase shift, which causes the oscillations. Since there are

many ways to get rid of the oscillations, such as focal series reconstruc-

tion (Schiske, 1973; Saxton, 1978; Van Dyck and Coene, 1987; Van Dyck

et al., 1993; Coene et al., 1996; Thust et al., 1996) and correction of the

spherical aberration (Rose, 1990), the Rayleigh resolution of the electron

microscope can be assumed to be given by the so-called information

limit, which is proportional to the inverse of the highest spatial fre-

quency that is still transferred with appreciable intensity. For simplic-

ity, it will ﬁ rst be assumed that the imaging process is linear. This

requires that the interaction between the electron and the object also

is linear, which means that there is a simple linear relation of the elec-

tron exit wave and the projected electrostatic potential. The electron exit

wave is a complex wave function in the plane at the exit face of the

object, resulting from the interaction of the electron beam with the

object. For example, the imaging process of weak phase objects, for

which the so-called weak phase object approximation holds (Buseck

et al., 1988), may be considered to be linear. If the object is a crystal,

viewed along a zone axis, the electrostatic potential of all the atoms

along the atom column is superimposed, which makes the interaction

very strong and highly nonlinear. In that particular case, due to the

focusing effect of the successive atoms, the scattering is increased to

Chapter 20 The Notion of Resolution 1233

higher angles. This effect is explained by the channeling theory (Howie,

1966; Van Dyck et al., 1989; Pennycook and Jesson, 1991; Van Dyck and

Chen, 1999). However, for amorphous objects, the atoms are stacked in

a disordered fashion, so that in projection their cores do not overlap,

except by coincidence. As a result, the interaction remains linear for

much larger object thicknesses and may be described by the weak

phase object approximation. If the imaging is linear, all transfer func-

tions have to be multiplied, or, equivalently, the point spread functions

have to be convolved. If it is assumed that all constituent point spread

functions are Gaussian, such as in Eq. (1), the resulting function is a

Gaussian as well, with a Rayleigh resolution ρ

determined by

= ρ

+ ρ

(7)

with ρ

the “width” of the electrostatic potential of the atom, ρ

the

Rayleigh resolution limited by thermal vibrations of the atom, ρ

the

Rayleigh resolution of the electron microscope, ρ

the Rayleigh resolu-

tion limited by the environment (vibrations and stray ﬁ elds), and ρ

Figure 20–1. Transfer functions of the different subchannels of electron

microscopic imaging.

1234 S. Van Aert et al.

the Rayleigh resolution limited by the detector. Today, for the best

electron microscopes, ρ

is somewhat below 1 Å (O’Keefe et al., 2001;

Kisielowski et al., 2001a; Batson et al., 2002a). In future instrumental

developments the Rayleigh and Sparrow resolution can be improved

by improving the resolutions of all different subchannels. However, a

factor that cannot be improved is ρ

, that is, the intrinsic “width” of

the atom itself. It is important to note that beyond a certain point, it

will be useless to further improve the Rayleigh resolution of the elec-

tron microscope since the transfer at high spatial frequencies is limited

by the scattering factor. It is already difﬁ cult to ﬁ nd suitable objects

that can be used to demonstrate the true Rayleigh resolution ρ

of an

electron microscope. Consider, for example, amorphous silicon. From

Figure 20–1, it follows that ρ

is about 1 Å. Therefore, for the best elec-

tron microscopes, it follows from Eq. (7) that for amorphous silicon

≈ 1 Å (8)

and from Eq. (4) that

≈ 0.7 Å (9)

From this example, it can be concluded that for the best electron micro-

scopes, the atoms themselves limit classical resolution criteria and

hence the diffraction limit. However, it should be noted that the discus-

sion of Rayleigh resolution and the diffraction limit is far more com-

plicated in case of nonlinear electron–object interaction, for example,

in the case of atom columns viewed along the column direction. It will

then also depend on the assumptions regarding the scattering of the

electrons on their way through the object. Furthermore, for coherent

imaging, such as in TEM, Goodman (1968) has shown that the Rayleigh

resolution will depend on the “phase distribution” associated with the

object. Depending on the relative phase associated with two atoms or

atom columns, the central dip in the composite image will be absent

or present. For particular values of the relative phase shift, the dip will

even be greater than the dip corresponding to an incoherent image of

these two atoms or atom columns. From this example, it can be con-

cluded that there is no simple generalization as to which type of

imaging, coherent or incoherent, is preferred in the sense of Rayleigh

resolution. So the assumption that incoherent imaging, for example

scanning transmission electron microscopy (STEM), will yield a

“better” resolution than coherent imaging, for example, TEM, is in

general not valid.

In the remainder of this chapter, it will be shown that by using super-

resolution algorithms, frequency components lying beyond the diffrac-

tion limit of the imaging system may be reconstructed. Then, other

deﬁ nitions of resolution are of interest.

3.3 Superresolution

Superresolution refers to reconstructing frequency components that lie

beyond the cutoff frequency of the imaging system. At ﬁ rst sight,

superresolution seems impossible. Knowledge of the system’s transfer

Chapter 20 The Notion of Resolution 1235

function makes it possible to reconstruct the object spectrum within

the passband of the imaging system by means of inverse ﬁ ltering of

the image spectrum, but frequency components beyond the diffraction

limit seem irrevocably lost. Indeed, in the absence of any restriction as

to the nature of the object, there are an inﬁ nite number of objects that

can produce the same image. Under certain conditions, however, super-

resolution is possible. The key to superresolution is prior knowledge.

For example, suppose that it is known that the object is of ﬁ nite size,

that is, it is nonzero only in a region of ﬁ nite extent. This single condi-

tion guarantees that the object spectrum is analytic. A well-known

property of an analytic function is that if it is known over a speciﬁ ed

interval, it can always be reconstructed in its entirety (Castleman,

1979). This process of reconstruction is called analytic continuation. It

can be shown that this method is perfect in theory. If the images are

noise free, it leads to an exact and complete reconstruction of the object

spectrum (Harris, 1964). However, noise limits its practical use (Frieden,

1967). Nevertheless, many effective superresolution algorithms (digital

image processing methods) have been proposed in the literature [for a

review, see Frieden (1975), Hunt (1994), and Meinel (1986)]. Both empir-

ically and theoretically, it has been shown that there are certain neces-

sary conditions to be satisﬁ ed by a superresolution algorithm to be

successful (Hunt, 1994). First, the algorithm should explicitly utilize a

mathematical description of the image formation process that relates

object and image via the point spread function of the imaging system.

Second, the images should be sufﬁ ciently oversampled to avoid alias-

ing after reconstruction of spatial frequencies beyond the diffraction

limit. For Nyquist sampled images (Gonzalez and Woods, 2002), the

algorithm should contain some suitable form of interpolation. Last, but

not least, the algorithm should contain prior knowledge of the object.

Examples of such prior knowledge used by superresolution algorithms

include the following:

• Finite extent of the object (as discussed above) (e.g., Harris, 1964;

Gerchberg, 1974, 1989).

• Positivity of the object (e.g., Schell, 1965; Biraud, 1969; Walsh and

Nielsen-Delaney, 1994).

• Upper and lower bounds on the object intensity (e.g., Janson et al.,

1970).

• Object statistics (e.g., Frieden, 1980; Hunt and Sementilli, 1992).

• Parametric model of the object.

Obviously, the performance of any superresolution algorithm will be

limited by noise. In the remainder of this chapter, we will assume that

the available prior knowledge of the object to be reconstructed consists

of a parametric model. Then, superresolution can be achieved by com-

puting the relatively small number of unknown parameters character-

izing the object from the available observations. In electron microscopy

these observations may be electron counting results made at the pixels

of a CCD camera. The image reconstruction problem thus becomes a

parameter estimation problem. For example, in the case of two-point

resolution, the object can be described by a two-component model

1236 S. Van Aert et al.

parametric in the locations of the point sources. Hence, if the point

spread function is known, a parametric model of the composite image

of the two-point sources can be derived. By ﬁ tting this model to the

image optimizing some criterion of goodness of ﬁ t, we obtain esti-

mates of the parameters of the model. For a correct model, in the

absence of noise, and apart from potential computational problems

that will be discussed in Section 4, this would result in a perfect

ﬁ t. That is, the object parameters can be estimated with unlimited

precision so that the object can be reconstructed perfectly. This means

that there would be no limit to resolution no matter how closely the

point sources are spaced. However, in practice it is noise that limits

the accuracy and precision with which parameters can be measured

and therefore limits the resolution. This will be the subject of Sections

5 and 6.

4 Deterministic Model-Based Resolution

Classical resolution criteria disregard the possibility of using prior

knowledge to extract analytic results from observations by means of

model ﬁ tting (den Dekker and van den Bos, 1997). In this section, prior

knowledge is taken into account in the form of a model describing the

observations. Thus far, the observations are assumed to be noise free.

Compared to Section 2, the model will be extended from two-peak

models to one or more-peak models. Instead of classical resolution, we

will speak of deterministic model-based resolution. It will be shown that

the relevant limits to deterministic model-based resolution are in any

case computational. However, if the model is inaccurate, which means

that it systematically deviates from the exact noise-free observations,

it will be shown that the relevant limits are both computational and

fundamental.

Imagine that Lord Rayleigh would image stars today. First, the image

of one star, which can be treated as a point object, will be considered.

Now, there exists a model for the object, namely that it consists of a

point. The point spread function of the telescope is also exactly known.

So, it is known how an image of one star should look like. Thus, there

is no interest in the detailed form of this image, but only in the position

of the star. The only objective of the experiment is to determine this

position. Obviously, in the absence of noise, numerically ﬁ tting the

known one-peak model to the image with respect to the position

parameter would result in a perfect ﬁ t. The resulting solution for this

location would be exact, and despite the blurring effect of the point

spread function, it imposes no limit to location resolution.

This line of reasoning can be extended to position measurements of

atoms or atom columns from noise-free electron microscopic observa-

tions. Suppose that these observations λ

are made at the pixels (k, l)

at the position (x

)

. The model that describes these observations is

called f

(τ) with τ the vector of unknown parameters, among which

are the locations of the atoms or atom columns. An example of such a

model is the following:

Chapter 20 The Notion of Resolution 1237

λτζ

πρ

ββ

kl kl

kxn lyn

(

)

−−

(

)

−−

(

)

exp

ρρ













∑

(10)

where ζ is the constant background, η

is the column-dependent height

of the Gaussian peak, ρ is the width of the Gaussian peak, n

is the total

number of atom columns, and β

and β

are the x- and y-coordinate

of the nth atom or atom column, respectively. The width ρ is supposed

to be identical for different atom columns. The parameter vector τ is

equal to (β

. . . β

xnc

. . . β

ync

. . . η

ρ ζ)

and contains R = 3n

+ 2

elements. The unknown parameters can be measured by ﬁ tting the

model to the observations. In a sense, we are then looking for the

optimum value of a criterion in a parameter space whose dimension is

equal to R, that is, the number of parameters to be measured. Each

possible combination of the R parameters can be represented by a point

in an R-dimensional space. The search for the global optimum of the

criterion of goodness of ﬁ t in this space is an iterative numerical opti-

mization procedure.

The problem may be of a computational kind. The existing optimiza-

tion methods fail if the dimension of the parameter space is so high

that it is not possible to avoid ending up at a local optimum instead of

at the global optimum of the criterion of goodness of ﬁ t, so that the

wrong structure is derived. To solve this dimensionality problem, that

is, to ﬁ nd a pathway to the global optimum, a good starting structure

is required, that is, initial conditions should be available for the param-

eters. For example, neighboring atoms or atom columns should be

discriminated in an image. In other words, the structure has to be

resolved. This corresponds to X-ray crystallography, where it is ﬁ rst

necessary to resolve a structure by using, for example, direct methods,

and afterward to reﬁ ne the structure. Moreover, the computing time

needed to reach convergence of the iterative procedure increases with

the dimension of the parameter space. In the following example, the

problems related to the study of the amorphous object with atomic

resolution TEM will be discussed. More details can be found in Van

Dyck et al. (2003).

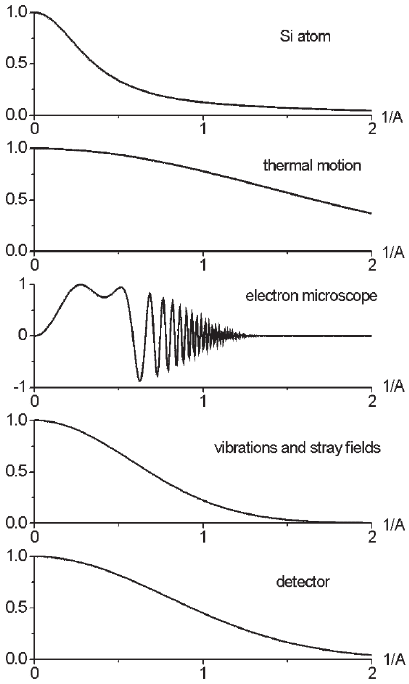
Example 1 (Amorphous Object) For an amorphous object, the number of

parameters increases with thickness. Therefore, from a certain thickness on, it

will be difﬁ cult to resolve the structure in projection. For example, consider

Figures 20–2 and 20–3. In Figure 20–2, the amorphous foil is thin, whereas

in Figure 20–3, it is thicker. Therefore, the number of projected atoms is larger

in Figure 20–3 than in Figure 20–2. It is clear that it will be more likely to

resolve the structure for the example given in Figure 20–2 than for that cor-

responding to Figure 20–3. To resolve the structure, it will be assumed that

the distances between neighboring projected atom positions should be larger

than or equal to the Sparrow resolution ρ

. The reason for choosing this crite-

rion is that the computer will then be able to distinguish the individual atoms,

since the observations are assumed to be noise free. However, it should be noted

that this criterion is not exact and, therefore, it will give only rough guidelines.

Suppose that the mean concentration of atoms per cubic ångstrom is equal to

1238 S. Van Aert et al.

V. T h e n, th e mean concentration A of projected atoms per square ångstrom is

given by

A = Vz (11)

where z is the thickness of the amorphous foil. On the other hand, if it is

assumed that each projected atom occupies a circle with a diameter equal to

the average distance d, averaged over distances between nearest-neighbor pro-

jected atoms, then

≈

(

)

(12)

From Eqs. (11) and (12), it follows that the thickness of the amorphous foil is

approximately given by

Figure 20–2. Amorphous

structure containing clearly

separable projected atoms.

Figure 20–3. Amorphous

structure containing severely

overlapping projected atoms.

Chapter 20 The Notion of Resolution 1239

≈

(13)

To resolve the structure and therefore to avoid dimensionality problems, it will

be assumed that the following condition is met:

d ≥ 2ρ

(14)

The factor 2 is arbitrarily chosen. Requiring that d is larger than or equal to

would not be sufﬁ cient. In that case, a substantial part of distances between

neighboring atoms would be smaller than ρ

and hence it is not possible to

resolve the structure. In principle, this can still occur if inequality (14) is ful-

ﬁ lled, but the probability that it occurs is lower. Then, it follows from Eqs. (13)

and (14), that

≤

πρ

(15)

For amorphous silicon, it follows from Eq. (9) that ρ

is approximately equal

to 0.7 Å and, furthermore, V is approximately equal to 0.05 atoms/Å

. Hence,

it follows from Eq. (15) that the amorphous silicon foil should not exceed thick-

nesses of the order of 13 Å so as to avoid dimensionality problems. This thick-

ness is rather small, which means that it is unrealistic to expect that atomic

resolution TEM is able to resolve amorphous silicon samples with realistic foil

thicknesses from only one projection (Cowley, 2001). It can thus be stated that

the structure of a realistic amorphous object cannot be determined from one

image alone. However, the situation can be improved drastically by using a

tomographic technique in which the sample is tilted and many projections from

different viewing directions are combined as shown in Figure 20–4. The

Fourier transform of a projection yields a section through the origin of the

three-dimensional Fourier space. By combining many different projections, it

is possible to reconstruct the whole Fourier space (Frank, 1992). In this way

an ideal microscope can resolve about one atom per cubic ångstrom, which is

sufﬁ cient to resolve amorphous structures.

In the foregoing, it has been assumed that the model is accurate.

However, if the model is inaccurate, the estimated position parameters

Figure 20–4. The principle of tomography.

1240 S. Van Aert et al.

may deviate from the true positions, even if the observations would be

noise free. This is called systematic error. Obviously, systematic errors

would place fundamental limits on deterministic model-based

resolution.

In this section, it has been shown that deterministic model-based

resolution is computationally limited. Computational problems can be

overcome only if the structure can be resolved. Moreover, if the model

is inaccurate, the resolution is also fundamentally limited, since this

results in a systematic error.

5 Statistical Model-Based Resolution

In Section 4, it was assumed that the observations are noise free.

However, in any real-life experiment, the observations will “contain

errors.” Then, the resolution depends fundamentally on the signal-to-

noise ratio in the detected image. In this section, the resolution will be

considered in the framework of statistical parameter estimation theory

and will be called statistical model-based resolution. It will be shown

that the relevant limits are both computational and fundamental.

Suppose there is a CCD camera that is able to count the individual

photons forming the image of a single point object or of two point

objects. The images as measured by this camera appear as in Figure

20–5 or as in Figure 20–6 for single or two-point objects, respectively.

The noise on these images stems from the counting statistics. The posi-

tion parameters can be estimated by numerically ﬁ tting the known

parameterized mathematical model to the images with respect to the

component positions, in the same way as expressed in Section 4.

However, if one repeated this experiment several times, one would,

due to the statistical nature of the observations, ﬁ nd different values

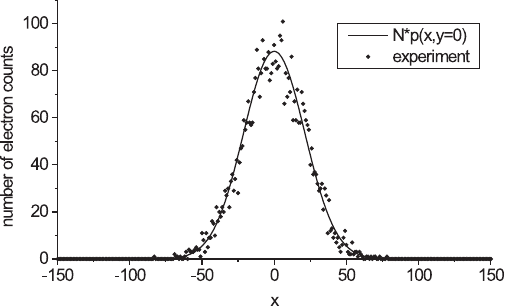
Figure 20–5. Simulation experiment of the image of a point as measured by

a CCD camera (300 × 300 pixels), with pixel size ∆x = ∆y = 1. The point spread

function used is a two-dimensional normalized Gaussian function p(x, y) as

in Eq. (1) with ρ = 21. The experimental as well as the expectation values N ×

p(x, y) are shown within the section y = 0. The number of imaging particles N

is equal to 250,000.

Chapter 20 The Notion of Resolution 1241

for the position or the distance estimates for single or two-point objects,

respectively. The position and distance estimates are statistically dis-

tributed about their mean values. Then, the obvious criterion to quan-

tify statistical model-based resolution is the precision of the estimate,

which is given by the variance of this distribution, or, by its square

root, the standard deviation. In a sense, the standard deviation is the

“error bar” on the position or on the distance. Applying statistical

parameter estimation theory, the attainable precision can be adequately

quantiﬁ ed in the form of the so-called Cramér–Rao lower bound (CRLB)

(van den Bos and den Dekker, 2001). This is a lower bound on the vari-

ance of any unbiased estimator of a parameter. It means that the vari-

ance of different estimators, such as, the least squares or the maximum

likelihood (ML) estimator, can never be lower than the theoretical

CRLB on the variance. Fortunately, the ML estimator attains the CRLB

asymptotically, that is, if the number of observations is sufﬁ ciently

large. Note that in accordance with the available literature, the CRLB

on the variance of the position estimate of the image of a single point

object and the CRLB on the variance of the distance estimate of the

image of two point objects are measures of what is called single-source

(Falconi, 1964) and differential (two-source) resolution (Falconi, 1967),

respectively. Single-source resolution is deﬁ ned as the instrument’s

capacity to determine the position of a point object that is observed in

a background of noise. Differential resolution is deﬁ ned as the instru-

ment’s ability to determine the separation of two point objects.

In this section the ﬂ uctuating behavior of the observations will be

described in Section 5.1 using parametric statistical models of observa-

tions. Next, in Section 5.2, it will be shown how an adequate expression

for the attainable statistical precision of the parameter estimates, that

is, the CRLB, can be derived from such a parametric statistical model.

Then, in Section 5.3, the ML estimator of the parameters will be derived

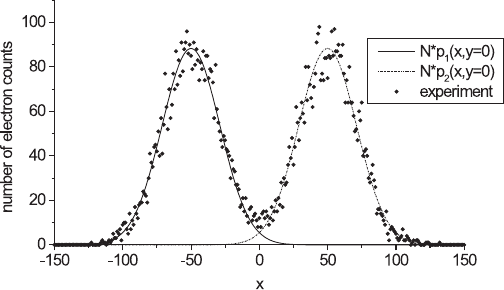
Figure 20–6. The results of a computer-simulated image of two neighboring

points. The experimental as well as the expectation values of the individual

peaks [N × p

1,2

(x, y)] are plotted within the section y = 0, where p

1,2

(x, y) are

two-dimensional normalized Gaussian point spread functions, as in Eq. (1).

The number of imaging particles 2N is equal to 500,000. The peaks are clearly

separable.