Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

1212 J.C.H. Spence

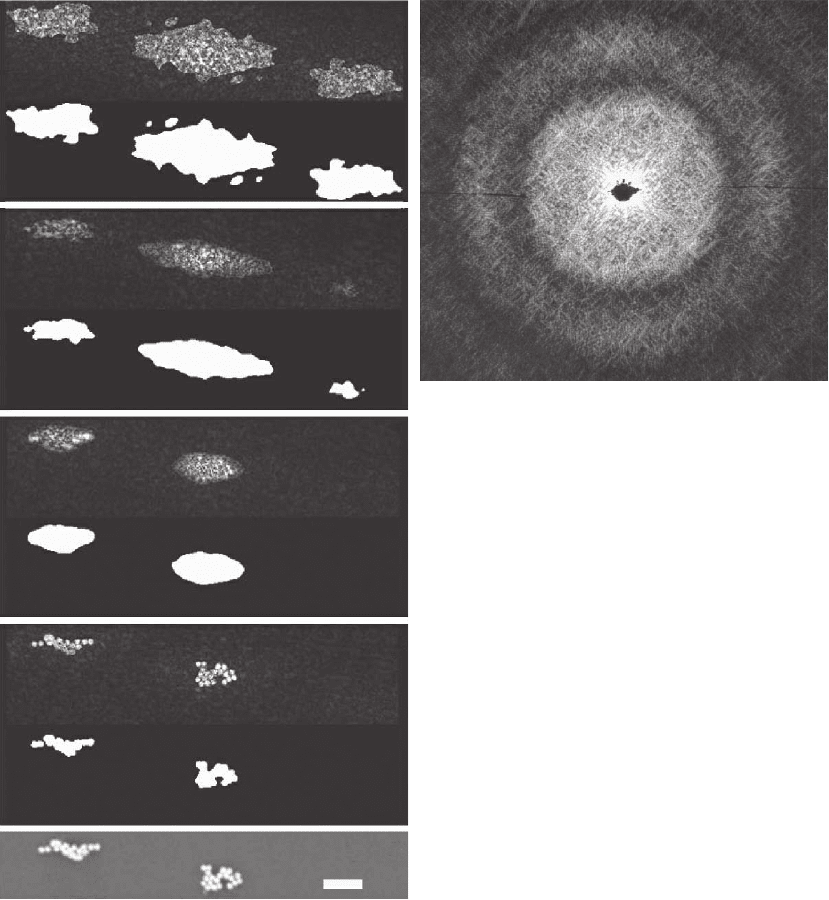
Figure 19–2A shows a transmission diffraction pattern obtained

using 600-eV monochromatic soft X-rays from clusters of gold balls,

50 nm in diameter, lying on a silicon nitride membrane. The silicon

nitride membrane is almost transparent to the X-rays, so the object

provides a useful test object for reconstruction. The pattern resembles

the Airey’s disk-like pattern from one ball, crossed by “speckle” fringes

due to interference between different balls. An image reconstruction

series using the shrinkwrap algorithm, in which the HIO algorithm

Figure 19–2. (A) Soft X-ray transmission dif-

fraction pattern from clusters of 50-nm gold

balls lying on a silicon nitride membrane. The

X-ray wavelength is 2 nm (600 eV). The resolu-

tion at the midpoint of the sides corresponds to

a spatial periodicity u

−1

= 17.4 nm, or a Rayleigh

resolution of 8.7 nm. (B) Image reconstruction

series using the shrinkwrap algorithm, in which

the HIO algorithm reﬁ nes the support during

iterations. The top image (a) is the centrosym-

metric autocorrelation function, with the support

estimate shown as a mask below. Intermediate

iterations lead to a ﬁ nal converged image of gold

ball clusters (e) shown at the bottom. The marker

is 1 µm in length. The inversion symmetry is lost

at (c).

Chapter 19 Diffractive (Lensless) Imaging 1213

reﬁ nes the support during iterations, is shown in Figure 19–2B. The

top image is the centrosymmetric autocorrelation function, with the

support estimate shown as a mask below. This mask was obtained by

Fourier transform of the diffraction pattern intensity (to produce the

autocorrelation function shown), followed by the selection of a contour

corresponding to a certain threshold of intensity. This thresholding

operation is repeated after each HIO-ER iteration cycle, to generate a

new improved estimate of the object support (see Marchesini et al.,

2003b, for details). Intermediate iterations lead to the ﬁ nal converged

image of the gold ball clusters (e) shown at the bottom. The marker is

1 µm in length. We note that the inversion symmetry necessarily pos-

sessed by the autocorrelation function at (a) is lost at (c) as it changes

smoothly into the correctly phased image.

Figure 19–3 shows an instructive case, indicating the way in which

“prepared objects” may be used to assist reconstruction. [Full experi-

mental details for CXDI are given in He et al. (2003), from which Figure

19–3 is taken.] Figure 19–3A shows a scanning electron microscope

(SEM) image of a set of gold balls lying on a silicon nitride membrane.

One ball at A is isolated. The autocorrelation function obtained from

an experimental soft X-ray transmission diffraction pattern (not shown)

taken from this object is given in Figure 19–3B. This may be interpreted

as the self-convolution of the object with its inverse, or, for a collection

of point-like objects, as the set of all interpoint vectors. Some interball

vectors are shown in Figure 19–3A and indicated again in Figure 19–3B.

The convolution of the single isolated ball A with the three balls at B

produces the autocorrelation function in Figure 19–3B a faithful image

of the three balls, blurred by the image of one ball. This process is

Figure 19–3. (A) SEM image of several clusters of gold balls, each 50 nm in diameter. Some interball

vectors are indicated. The balls lie on an X-ray transparent substrate. (B) The Fourier transform of the

X-ray diffraction pattern taken from (A). This is the autocorrelation function of the density in (A) and

is a map of all interball vectors or the self-convolution of the object with its inverse. Because the object

in (A) includes a single isolated ball at A, the vector AB leads to a faithful image of the triple-ball

cluster at B. (The convolution of one ball with three gives a blurred image of three.) (From He

et al., 2003.)

1214 J.C.H. Spence

similar to the heavy-atom method of X-ray crystallography, or the

method of Fourier transform holography in optics (Collier et al., 1971).

If such a gold ball or strong “point” scatterer can be placed near an

unknown object, the autocorrelation function will contain a useful ﬁ rst

estimate of the desired image of the unknown, which can also be used

to provide a support for further HIO iterations aimed at improving

resolution. This process is demonstrated in He et al. (2004), where, fol-

lowing the original suggestion of Stroke (1997), it is found that the

resolution in the autocorrelation “image” may be considerably improved

beyond the size of the reference ball by simple deconvolution. By using

a larger reference object, or one consisting of a cluster of small balls,

the intensity of scattering from the reference object can be increased.

It has been noted that a randomly placed cluster of point scatterers can

provide a high resolution image in Fourier transform holography when

used as a reference object (see He et al., 2004; Collier et al., 1971; Eisebett

et al., 2004, for more details and references).

The ﬁ rst successful application of CDI to the electron diffraction

patterns provided by a transmission electron microscope (TEM) is

described in Weierstall et al. (2001), where a complete description of

the method can be found. An important asset of the TEM is its ability

to provide an image of the same region that contributes to the micro-

diffraction pattern, so that this image can be used to supply the support.

However, electron scattering is so strong that any scattering contribu-

tion from a supporting ﬁ lm, however thin, is found to prevent success-

ful CDI. The resolution of the best TEM instruments in direct

phase-contrast imaging mode using lenses is now about 1 Å. Figure

19–4 shows a more recent application of CDI to an electron diffraction

pattern using a TEM (Zuo et al., 2003). This remarkable image is the

ﬁ rst atomic-resolution CDI image, and possibly the ﬁ rst atomic-

resolution image of a nanotube. The image gives us the helicity of the

tube, its dimensions, and the number of walls. The double-walled

nanotube spans a hole in a thin amorphous carbon ﬁ lm, while the

electron beam diameter (about 50 nm) is smaller than the hole, so that

there is no background contribution from the carbon ﬁ lm. A conven-

tional TEM image was used to provide the support function for HIO

iterations along the edges of the tube, and it is suggested that the

boundary of the support across the tube is provided by loss of coher-

ence at the edge of the electron probe due to rapid phase variations

arising from the aberrations of the probe-forming lens. (In general a

tight support is desirable for CDI.) The image shows higher resolution

detail than conventional TEM images of nanotubes. Resolution is

limited perhaps only by the temperature factor, or by distortions in

electron lenses used to magnify the diffraction pattern. It remains to

be seen if tomographic imaging at atomic resolution is simplest by this

method or by direct TEM imaging using lenses. If CDI is used, the

difﬁ cult problem of supporting a nanoparticle for diffraction over a

range of orientations will need to be solved. Radiation damage may be

reduced in diffraction mode under some conditions.

Three-dimensional (tomographic) CDI of inorganic samples has now

been demonstrated (Miao et al., 2002; Williams et al., 2003; Chapman

Chapter 19 Diffractive (Lensless) Imaging 1215

et al., 2006) using soft X-rays at a resolution of about 10 nm. This raises

hopes of direct imaging, for example, of whole cells by this method if

radiation damage considerations allow this at usefully high resolution.

The X-ray source is a synchrotron and undulator, providing coherent

Figure 19–4. (A) Electron microdiffraction pattern from a single double-

walled nanotube. This consists of a rolled-up sheet of graphite. Fine details

arise from the helical structure (Zuo et al., 2003). (B) At left is the experimental

image of the double-walled nanotube reconstructed from the electron diffrac-

tion pattern in (A). At right is shown a corresponding model of the structure

(Zuo et al., 2003).

1216 J.C.H. Spence

radiation at about 600 eV. In recent work (Chapman et al., 2006), a

simple zone plate was used as a monochromator, following by a beam-

deﬁ ning aperture of about 10 µm in diameter, coherently ﬁ lled. A nude

soft X-ray CCD camera, employing 1024 × 1024 24-µm pixels was used.

The sample is mounted in the center of a silicon nitride window ﬁ tted

to a TEM single-tilt holder, which provides automated rotation about

a single axis normal to the X-ray beam. The window is rectangular,

with the long axis normal to both the beam and the holder axis. Dif-

fraction patterns are recorded at 1° rotation increments, with a typical

recording time of about 15 min per orientation. The maximum tilt angle

is then limited by the thickness of the silicon frame around the window

to perhaps 80°, resulting in a missing wedge of data. In addition, data

may be missing around the axial beamstop. The development of

software for automated tomographic diffraction data collection and

merging is a large undertaking (Frank et al., 1996), and much can be

learned from the prior experience of tomography in biological electron

In that case, however, the registration of successive images at different

tilts is greatly facilitated by direct observation of image features. The

use of shadow images or X-ray zone-plate images for similar purposes

has been suggested. With no direct imaging mode, much time is wasted

in X-ray work locating the beam on the sample, which, with current

CCD detectors, will typically be smaller than 2 µm in diameter. The

ﬁ nal resolution (in one dimension), allowing for an “oversampling”

factor of 2, will then be 4000/1024 = 3.9 nm. The camera length (sample-

to-detector distance) of the diffraction camera must then be selected to

allow half this spatial frequency to fall at the edge of the CCD camera

at u

max

= θ

max

/λ = 0.5/3.9 nm

−1

, so that the maximum scattering angle is

max

= 0.25 rad for λ = 2 nm. Then the ﬁ nest periodicity in the object

(3.9/0.5 nm) is sampled twice in every period, according to Shannon’s

requirement (two points are required to deﬁ ne the period and ampli-

tude of a sine wave if aliasing is excluded). For a CCD with linear pixel

number N, the ratio of the ﬁ nest detail to largest dimension is N/2, so

that developments in detector technology limit CDI. The transverse

spatial coherence of the beam must exceed 4 µm, as discussed together

with monochromator requirements below.

Tomographic or three-dimensional imaging can provide the ability

to “see inside” an object, but this requires that the intensity at a point

in a projection be proportional to a line integral of some simple prop-

erty of the object, such as the charge density. Then methods such as

ﬁ ltered back-projection can reassemble these two-dimensional projec-

tions into a volume density. Contours of equal density may then be

isolated and presented to show the internal structure. For CXDI, a dif-

ferent approach is used, and some simpliﬁ cations occur. It is no longer

necessary to make the resolution-limiting “ﬂ at Ewald sphere” approxi-

mation, since diffraction data collected at one tilt can be assigned to

points lying on the curved Ewald sphere in reciprocal space. (This is

the momentum and energy-conserving sphere that describes elastic

scattering in reciprocal space.) The sample is then rotated through this

sphere around a single axis, until all of the reciprocal space is ﬁ lled,

microscopy, where these techniques have been perfected (Frank, 2006).

Chapter 19 Diffractive (Lensless) Imaging 1217

out to a given resolution. Three-dimensional interpolation of data

points near the sphere is needed, and careful intensity scaling may be

necessary if several exposures with different times are required to

cover the full dynamic range of the data. It is often found that missing

data points in the central region can be treated as adjustable parame-

ters in the HIO iterations. Once a roughly spherical volume has been

ﬁ lled in reciprocal space (perhaps with missing wedge and beam-stop

region), the three-dimensional iterations of the HIO algorithm may be

applied [Eqs. (8), (9), etc., extended to three dimensions]. The comput-

ing demands are severe, as outlined below. The converged data will

provide a three-dimensional density map, proportional to the local

charge density, if the single-scattering approximation of X-ray diffrac-

tion theory applies and if the spatial variation in attenuation of the

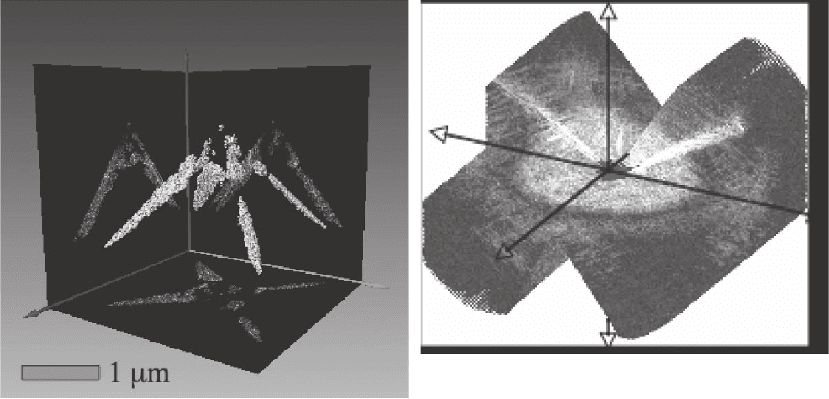
beam due to the photoelectric effect can be neglected. Figure 19–5

shows such a tomographic reconstruction, from which three-dimen-

sional surfaces of constant density may be obtained. These surfaces

allow us to “see inside” materials, and may eventually permit maps

to be obtained that distinguish regions of different chemical

composition.

The usefulness of tomographic CXDI in biology remains to be deter-

mined; at present the method appears to have the advantages over

electron microscopy by allowing observation of thicker samples under

a wider range of environments (for example, in the “water window”

around 580 eV for soft X-rays). By comparison with X-ray zone-plate

“full-ﬁ eld” imaging, the method allows a much larger numerical aper-

ture to be used, and hence makes more efﬁ cient use of scattered

Figure 19–5. (A) Tomographic reconstruction from a soft X-ray diffraction pattern shown in (B). The

object consists of gold balls (50 nm diameter) lying along the edges of a pyramidal-shaped silicon

nitride structure. This is one image from a rotation series. From the complete series, three-dimensional

surfaces of constant density can be constructed. (B) The volume of soft X-ray diffraction data collected

to obtain the three-dimensional reconstruction in (A). (See color plate.)

1218 J.C.H. Spence

photons, while providing potentially higher resolution. At high resolu-

tion the depth of focus λ/θ

may become less than the sample thick-

ness, which prevents tomographic reconstruction by back-projection

methods based on simple projections. Then tomography may best be

undertaken using optical sectioning rather than reconstruction from

projections. CDI, based on three-dimensional diffraction data, pro-

vides a third alternative. The resolution limit imposed by radiation

damage in CXDI, as expressed by the Rose equation (Spence, 2003),

remains to be determined experimentally, but is likely to be signiﬁ -

cantly poorer than 1 nm, which has already been achieved in three-

dimensional single-particle electron microscopy of proteins. Howells

et al. (2005) and Marchesini et al. (2003a) provide a detailed discussion

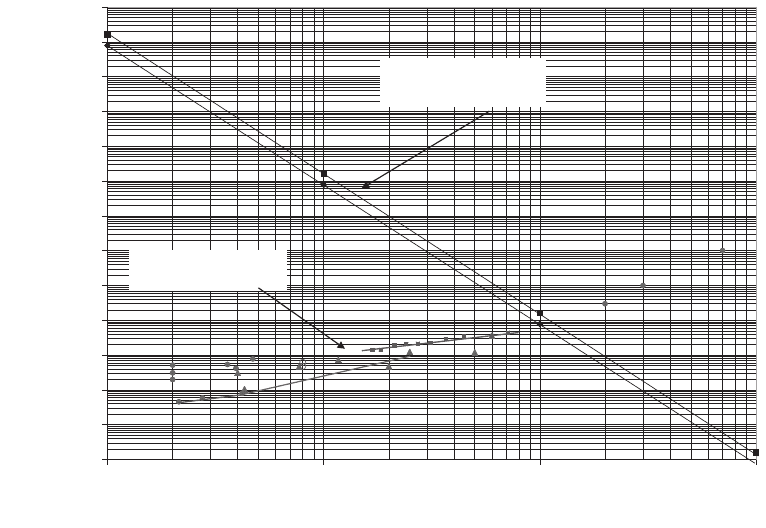
of this large subject, including a plot of dose against resolution for

various microscopies in biology, as discussed in Section 9, shown in

1.0E+05

1.0E+06

1.0E+07

1.0E+08

1.0E+09

1.0E+10

1.0E+11

1.0E+12

1.0E+13

1.0E+14

1.0E+15

1.0E+16

1.0E+17

1.0E+18

0.1 1 10 100

Resolution (Å)

Dose(Gy)

(ROSECRITERION)

MAXIMUM TOLERABLE

DOSE

REQUIRED IMAGING DOSE

Figure 19–6. Summary of experimental measurement on organics for various microscopies on a plot

of dose against resolution (Howells et al., 2005). Literature experimental values (e.g., Reimer, 1989) are

shown as follows: Filled circles are from X-ray crystallography, ﬁ lled triangles from electron crystal-

lography, open circles from single-particle electron cryoelectron microscopy, open triangles from

electron tomography, diamonds from soft X-ray microscopy, and ﬁ lled squares from recent X-ray

crystallography work on spot-fading experiments by Holton on the ribosome at the Advanced Light

Source. Viable single-molecule microscopies must fall above the Rose equation line (to give a statisti-

cally signiﬁ cant image) and below the maximum tolerable damage line. Those below the Rose equation

line succeeded by using crystallographic redundancy and form a periodically averaged image of

perhaps 10

molecules in a crystal. The required imaging dose is calculated for a protein of empirical

formula H50C30N9O10S1 and density 1.35 g/cm

against a background of water, imaged with 10 keV

X-rays (upper Rose line) and 1 keV (lower Rose line).

Chapter 19 Diffractive (Lensless) Imaging 1219

Figure 19–6 (see also Henderson, 1995). The dose-fractionation theorem

of Hegel and Hoppe is also relevant (Reimer, 1989). Recently, dramatic

images of whole yeast cells have been imaged by CDI (Shapiro et al.,

2005) using the apparatus described by Beetz et al. (2005).

6 Iterated Projections

A breakthrough in understanding the remarkable success of the HIO

algorithm occurred in 1984, when Levi and Stark (1984) (based on

earlier work by Youla and Webb, 1982) showed that the algorithm could

be understood as successive Bregman projections between convex and

nonconvex sets. Here an image is represented as a single vector R in

an N-dimensional space, with one coordinate for each pixel. The addi-

tion of two such vectors adds together two images. Distance between

images (vectors) in this space has the form of the familiar χ

goodness

of ﬁ t index, so that similar images are near each other. The set of all

images subject to a given constraint (e.g., known symmetry, known

Fourier modulus, known sign of density, known support) is considered

to occupy a volume in this space. The operation of taking a current

estimate of the image, performing a Fourier transform, replacing the

magnitudes of the diffracted amplitudes with the measured values,

and inverse transforming was shown to be a projection onto the set of

images subject to the Fourier modulus constraint. Vectors R between

the boundaries of two constrained sets of images are considered. If it

is shown that all the images within the only overlap between two

constrained sets are equivalent solutions, then the phase problem

reduces to ﬁ nding this volume, where R = χ

and the ER error metric

are a minimum. Constraints may be of two types—convex and non-

convex. For a convex set, all points on any line segment terminating

within the set lie inside the set. A set P is convex if αR + (1 − α)R′ lies

within P for all R and R′. Here 0 < α < 1 is a scalar deﬁ ning position

along the line. In two dimensions, a kidney-shaped set is nonconvex

and an ellipse is convex. Bregman has shown that iterative projections

between convex sets must lead directly to a unique solution if it exists,

without stagnation. In this manner the global optimization problem is

solved without an exhaustive search for the case in which a unique

solution and convex constraints are known to exist. For our problem

the Fourier modulus constraint (the known diffraction intensities) is

nonconvex, so that this approach has been of limited value. However,

it provides a powerful geometric way of thinking about the algorithm

as a trajectory in Hilbert space, which is usually drawn in two dimen-

sions for simplicity. The effects of variations in feedback parameter β

can be understood, convergence properties studied, and new algo-

rithms proposed. For the ER algorithm, the path is a zig-zag between

the boundaries of sets; for the HIO it is a spiral. Some desirable convex

constraints include known support, a knowledge of phase rather than

amplitude, the sign constraint, symmetry, a known histogram of

density levels (Zhang and Main, 1990) (such as exists for proteins),

1220 J.C.H. Spence

entropy minimization, and (for nonoverlapping atoms) atomicity. A list

of constraints used in protein crystallography can be found in the rel-

evant section of volume F of the international tables on crystallography.

Application of these constraints thus avoids the common problem

whereby optimization programs become trapped in local minima.

The application of constraints can be viewed as projections in the

N-dimensional space. Recall that the support S is deﬁ ned as the set of

points for which the density is nonzero. For example, application of the

support constraint P

corresponds to setting many pixels to zero, that

is, to projecting onto a space of lower dimension. For the Fourier

modulus constraint, we note that Parseval’s theorem ensures that dis-

tances in the N-dimensional real space are equal to those in a similar

N-dimensional space of Fourier coefﬁ cients. Consider an Argand

diagram for a particular Fourier component, for which the modulus

constraint restricts solutions to a circle, whose radius is given by the

measured value of the Fourier modulus. An estimate provided by the

algorithm (e.g., outside this circle) must be projected (by operator P

)

onto the nearest point on the circle, along a line that will pass through

the origin. (This corresponds to the numerical process during one itera-

tion of retaining the current phase estimate, but replacing the magni-

tude with the measured magnitude, in the HIO algorithm.) Since the

linear addition of two vectors terminating on the circle does not

produce a third that terminates on the circle, the modulus constraint

is not convex. Note, however, that the addition of two vectors of arbi-

trary length but equal phase produces a new complex number with the

same phase, so that a knowledge of phase is a convex constraint, and

thus more powerful than a knowledge of amplitudes. The identity

operation I is also useful, and a reﬂ ector operation R

= 2P

− I can be

deﬁ ned, which reverses the sign of the density outside the support S.

Using these operators, all the iterative algorithms can be represented

simply and analyzed as alternating projections onto convex (and non-

convex) sets (POCS). In this context, we may deﬁ ne these more limited

projections as “projectors,” which takes a given vector R to the nearest

point of a nearby constrained set (usually on its boundary). Then

1. The error-reduction (ER) (Gerchberg–Saxton) algorithm may be

written

(n+1)

= P

(n)

2. The charge-ﬂ ipping (CF) algorithm may be written

(n+1)

= R

(n)

3. The hybrid input–output (HIO) algorithm may be written

(n+1)

(r) = P

(n)

(r) if r ∈ S

(n+1)

(r) = (I − β)P

(n)

(r) if r ∉ S

4. The averaged successive reﬂ ections (ASR) algorithm may be

written

(n+1)

= 0.5(R

+ I)ρ

(n)

Chapter 19 Diffractive (Lensless) Imaging 1221

Similar descriptions of the difference map method (Elser, 2003), the

hybrid projection reﬂ ection (HPR) (Bauschke et al., 2002), and the

relaxed averaged alternating reﬂ ectors (RAAR) (Luke, 2005) have been

given. For β = 1, the HIO, HPR, ASR, and RAAR algorithms are identi-

cal. A comparison of the performance of all of these, together with the

powerful shrinkwrap algorithm (HIO with dynamic support) and

simple geometric representations of the trajectory of the error metric

for few-dimensional cases, can be found in Marchesini (2006).

Using this approach, it has also been shown that the HIO algorithm

is equivalent to the Douglas–Rachford algorithm, and is related to clas-

sical convex optimization methods (Bauschke et al., 2002). The text by

Stark (1987) is recommended as a tutorial introduction to this large

subject.

7 Coherence Requirements for CDI: Resolution

It is readily shown (Spence et al., 2004) that the lateral or spatial coher-

ence requirement for diffractive imaging is, in one dimension, that the

coherence width X

∼ λ/θ

be at least equal to twice the largest lateral

dimension W of the object. (This is similar to the requirement in crys-

tallography that X

exceed the dimensions of a primitive unit cell to

avoid overlap of Bragg beams, with beam divergence θ

. For phasing

by the oversampling method, this cell must be about twice as large as

the molecule.) This ﬁ xes the incident beam divergence and hence the

exposure time for a given object size and source. Since at the unaper-

tured diffraction limit (Θ = 90°) the resolution is approximately equal

to the wavelength and about two pixels are required per resolution

element, a total of about (4X

/λ)

image pixels would be needed for a

coherence width X

and oversampling factor 2. Physically, this just

means that the coherence patch must include the “known” region of

vacuum (zero density) surrounding the object boundary (support). It

is necessary to diffract coherently from an area twice as large as the

isolated object of interest.

The temporal coherence length L

is also important. For a ﬁ eld of

view W at the object (so that the ﬁ rst oversampling point occurs at

scattering angle λ/W) and ﬁ nest (bandlimited) object spatial frequency

−1

, the optical path difference between points on opposite sides of the

object and a distant detector point is W sin θ = Wλ/d, which should not

exceed the longitudinal coherence length for X-rays L

= λE/∆E. Hence

the fractional energy spread allowable in the beam to record spatial

frequency d

−1

is E/∆E > W/d = N, where d is the sampling interval

in the object and N the linear number of pixels needed to sample

the object space in the HIO algorithm. A more detailed calculation,

considering the shape of the temporal coherence function, gives the

requirement on longitudinal coherence as about E/∆E > N/3, which

improves on the estimate in Spence et al. (2004). This determines the

quality of the monochromator needed. In practice values of E/∆E = 500

have yielded good results in soft X-ray work using CCD detectors with

pixels, where N = 1024. Then the in-line arrangement of a simple