Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

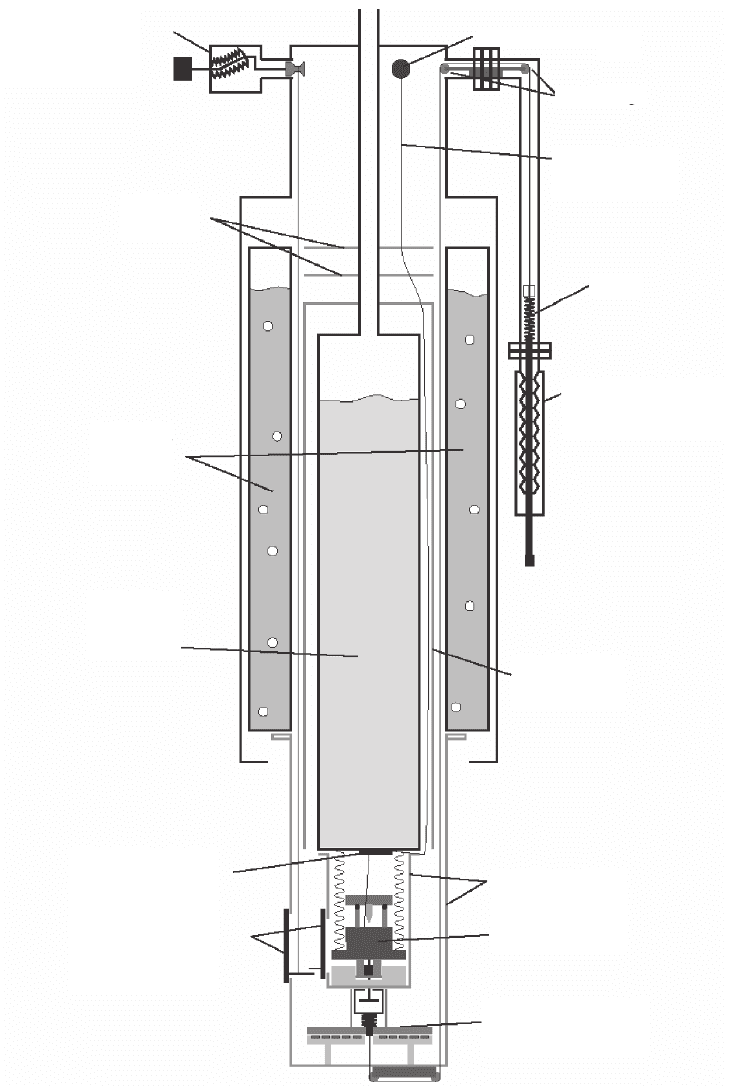
1080 U. Weierstall

electrical feedthroughs

ball bearing

cabeling

(stainless steel)

spring

linear feedthrough 4”

(to pull down the STM)

He gas cooled

radiation shield

radiation shields

(LN,

LHe)

STM head

eddy current damping

for the LHe cryostat

shutter for sample

& tip transfer

STM-contacts

(37-pin plug)

LHe dewar

(41)

dewar

(141)

baffles

rotary feedthrough

(transfer shutter)

Figure 17–7. Design of the LT-STM by Prof. Rieder and Dr. Meyer (Free University Berlin), courtesy

of CreaTec GmbH, distributed by SPECS GmbH.

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1081

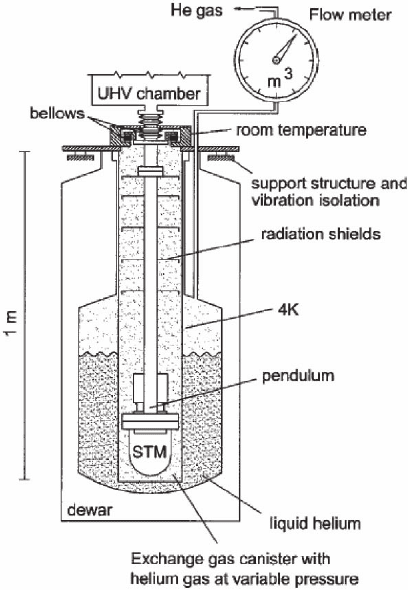
The LT-STM build by D. Eigler (Eigler et al., 1990) at IBM-Almaden

and a similar instrument at Berlin are different from the previous two.

In both previous instruments, the STM vacuum system and the isola-

tion vacuum of the He and nitrogen reservoirs are connected. In the

Eigler design the cryogenic vacuum system is not connected to the

STM vacuum system. Instead the STM is mounted at the end of a

bellows-supported evacuated pendulum with a resonance frequency

of about 0.6 Hz. Helium exchange gas provides thermal coupling as

well as acoustic isolation between the surrounding liquid helium

dewar and the STM ﬂ ange. The temperature of the STM can be set by

controlling the helium gas pressure in the exchange gas chamber (Rust

et al., 2001) (see Figure 17–8). In all designs, mechanical disturbances

from bubbling liquid nitrogen in the surrounding liquid nitrogen cryo-

stat can be prevented by solidifying the nitrogen by pumping it with

a rotary pump (which is located far from the microscope) (Jeandupeux

et al., 1999).

3 Applications

There is a large volume of literature on experiments using a LT-STM

covering electronic structure and lifetime measurements, measure-

ments on superconductors, atomic and molecular manipulations,

molecular vibrational spectroscopy, photon-emission spectroscopy,

Figure 17–8. Illustra-

tion of the basic design

principle for the Eigler-

style low-temperature

STM. The STM is

mounted at the end of a

bellows-supported pen-

dulum, which is encap-

sulated in an exchange

gas canister inside of a

liquid helium dewar.

Limited variable tem-

perature operation is

possible by controlling

the exchange gas pres-

sure. (From Rust et al.,

2001.)

1082 U. Weierstall

and measurements of magnetic properties with spin polarized elec-

trons. We can discuss only a small subset of the work done and refer

to the literature for further reading. For the applications shown here,

low-temperature operation of the STM has proven to be essential.

3.1 Electronic Structure

Understanding the distribution and response of electrons in solids, the

electronic structure, is key to explaining and exploiting fundamental and

technologically important properties of materials. The method of

choice to obtain information about the electronic structure of solids

and surfaces in the past decades has been angle-resolved photoemis-

sion spectroscopy (ARPES) and inverse photoemission spectroscopy

(IPES). The development of low-temperature scanning tunneling

microscopes operating under ultrahigh vacuum conditions has pro-

vided new opportunities for investigating electronic states at metal

surfaces. At low temperatures, due to reduced broadening of the Fermi

level of the STM tip and sample, rather high-energy resolution is

achievable. Moreover, the absence of diffusion together with the spatial

resolution of the STM enables detailed studies of the interaction of

electronic states with single atoms and other nanoscale structures.

3.1.1 LDOS Oscillations

Electrons occupying surface states on the close-packed surfaces of

noble metals are bound in the direction perpendicular to the surface,

but have free-electron-like characteristics parallel to the surface

(Gartland and Slagsvold, 1975; Heimann et al., 1977; Zangwill, 1988).

On the (111) face of noble metals these surface states arise as a result

of the gap that exists along the Γ–L line in their bulk Brillouin zone

(Shockley, 1939). Surface state electrons play an important role in a

variety of physical processes, including epitaxial growth (Memmel and

Bertel, 1995), in determining equilibrium crystal shapes (Garcia and

Serena, 1995), molecular ordering (Stranick et al., 1994a), surface cataly-

sis (Bertel et al., 1995), and physisorption (Bertel, 1997).

Surface state electrons scattered form defects and step edges give

rise to quantum interference patterns in the electron density, which

can be probed using the scanning tunneling microscope (Davis et al.,

1991). Standing wave patterns in the LDOS on the Cu(111) surface have

been observed with an LT-STM for the ﬁ rst time by Crommie et al.

(1993b). LDOS oscillations at surfaces are the analog to the Friedel

oscillations of the total charge density (Friedel, 1958). The experiments

where done at 4 K in an LHe bath cryostat STM (Eigler and Schweizer,

1990). Figure 17–9 shows a constant current image of the Cu(111) surface

with static spatial oscillations in the ILDOS. The oscillations decay

away from step edges and point defects and have a characteristic

period of ∼15 Å. The amplitude of the corrugations is ∼0.02 Å and is

greater near the top of step edges than near the bottom. Spatial varia-

tions in the LDOS of the surface at the energy E = E

+ eV can be

approximately mapped out by measuring dI/dV at bias voltage V

(Crommie et al., 1993b). Figure 17–10 shows dI/dV linescans as a func-

tion of distance to a monoatomic step on Cu(111). The wavelength of

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1083

Figure 17–9. Standing wave patterns on copper: constant current image of

the Cu(111) surface (V = 0.1 V, I = 1.0 nA). Three monoatomic steps and several

point defects are visible. Spatial oscillations of the tunneling current originat-

ing from step edges and defects are evident. Image size: 500 Å × 500 Å. (From

Crommie et al., 1993b.)

Figure 17–10. Spatial dependence of dI/dV, measured as a function of distance

(along upper terrace) from step edge on Cu(111) at different bias voltages. Zero

distance corresponds to the lower edge of the step. The measured wavelength

of the surface LDOS oscillations changes as a function of energy. Solid lines,

experiment; dashed lines, theoretical ﬁ t modeling the surface as a two-

dimensional electron gas in the presence of a single hard wall barrier. Inset

shows the extracted values of k plotted against energy deﬁ ning an experimen-

tal dispersion curve of the surface state. (From Crommie et al., 1993b.)

1084 U. Weierstall

the oscillation in the surface LDOS increases with decreasing energy.

At ∼0.45 eV below E

the LDOS sharply decreases in magnitude. Mea-

suring a full dI/dV spectrum at a ﬁ xed point on the surface revealed

the origin of this transition: Figure 17–11 shows dI/dV spectra recorded

with a stationary tip away from steps and on a step while ramping the

bias from 1.0 to −1.0 V. The spectra taken on a terrace show a sharp

drop in dI/dV at V ≈ −0.45 V. This corresponds to a sudden decrease in

the surface LDOS at energies more than 0.45 eV below E

and marks

the bottom of the Shockley surface state band on Cu(111).

By ﬁ tting the oscillations of the dI/dV linescan data to a simple free

particle model with hard-wall conﬁ nement at surface steps, the major

features of the spectra could be explained and a value of the surface

state electron wavevector k

for each electron energy could be extracted.

A plot of these electron wavevectors against electron energy resulted

in an experimental dispersion curve, as shown in the inset of Figure

17–10. The k

data for different energies E − E

were ﬁ tted with the

dispersion relation for electrons conﬁ ned to two dimensions (dotted

curve in inset of Figure 17–10):

Ek E







(

)

(4)

where E

is the surface state band edge, m* is the effective mass of the

surface state electron, and

kkk

xy

is the electron wavevector

parallel to the surface. This procedure yielded the surface state effec-

tive mass m* = 0.38 ± 0.02m

and the surface state band edge E

= −0.44

± 0.01 eV below E

. The extracted value of the surface state band edge

matched the location of the peak in the dI/dV spectrum of Figure 17–11.

The measured values where roughly in agreement with previous pho-

toemission results.

In the previous example, scattering of surface state electrons has

been modeled as scattering at inﬁ nite potential walls. However, absorp-

Figure 17–11. Differential conductance dI/dV spectra taken with tip over

clean terrace (solid line) and over the center of a step edge (dashed line). The

increase at ∼0.45 V is due to the onset of the Cu(111) surface state. (From

Crommie et al., 1993b.)

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1085

tion processes at step edges due to bulk coupling are disregarded with

this model.

Therefore, a Fabry–Perot resonator model with a step reﬂ ection

amplitude and scattering phase has been introduced to analyze the

measured LDOS patterns of electrons conﬁ ned between two parallel

steps on Ag(111) at 4.9 K. (Burgi et al., 1998). The electron reﬂ ectivity

has been found to be independent of crystallographic step structure,

but depends on the step morphology (ascending, descending). Reﬂ ec-

tivity and scattering phase could be quantiﬁ ed for any two parallel

steps, providing insight into the scattering mechanism.

It has been assumed so far that for measurements close to E

(small

bias voltage), the LDOS and ILDOS are essentially the same, i.e., a

constant-current image (topograph) and a dI/dV differential conduc-

tance image should be identical. However, with increasing bias voltage

the constant-current image should systematically diverge from the

LDOS (dI/dV) as states from a range of energies contribute to the inte-

grated state density.

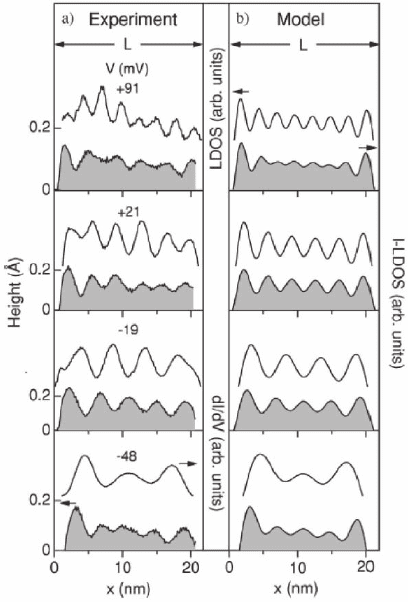
One-dimensional electron conﬁ nement has been used to measure

the bias-dependent difference between the ILDOS and LDOS (Pivetta

et al., 2003) with a low-temperature STM. The measurements where

performed in a home-built STM, operating in UHV at 4.8 K (Gaisch

et al., 1992). The system studied was a quantum box consisting of two-

dimensional surface states on Ag(111) conﬁ ned by two parallel surface

steps (see Figure 17–12). Constant current cross sections (measuring

the ILDOS) and dI/dV cross sections (measuring the LDOS) from the

quantum box perpendicular to the steps were compared at different

bias voltages. Oscillations in both, constant current and dI/dV curves

were observed (Figure 17–13). These oscillations are due to the interfer-

ence of the incident and scattered surface state electrons at the box

boundaries. The measured data were compared with a model calcula-

tion of the LDOS and ILDOS assuming a free particle model with hard

wall conﬁ nement at surface steps.

The surface state electrons are free in the direction parallel to

the steps, but due to the boundary conditions given by the one-

dimensional conﬁ nement in a box of width L, the component of the

electron wavevector perpendicular to the step edges is quantized: k

Ⲛn

= πn/L. Each corresponding eigenenergy E

Ⲛn

) deﬁ nes the onset of a

one-dimensional subband E

), where E(k

) is the dispersion relation

(4) for the Ag(111) surface state electrons. Since the tunneling current

I is calculated by integrating over all energies between the bias eV and

, it contains contributions from several subbands E

). Calculating

the differential conductance dI/dV also requires integration of the DOS

over a small range of energies given by the modulation amplitude used

for lock-in detection (here 1–10 mV). Comparison of the model calcula-

tions and experimental measurements could explain the observed

oscillation patterns in I and dI/dV in terms of the way in which differ-

ent subbands contribute to the signals. The measured data of Pivetta

et al. (2003) indicate that the difference between differential conduc-

tance and constant-current measurements can already be pronounced

for bias voltages as small as 19 mV. Thus, even close to E

, the interpre-

1086 U. Weierstall

tation of constant current images in terms of the LDOS may not be

fully correct.

3.1.2 Energy Dispersion Measurements

Energy dispersion measurements as a function of the electron wave-

vector E(k) of surface states on metals is usually performed by tech-

niques such as ARPES for occupied states or IPES for empty states,

which are selective in both energy and wavevector. As show in Section

3.1.1, the energy dispersion relation of the surface state can also be

measured with scanning tunneling spectroscopy (STS) by measuring

the LDOS on single line scans perpendicular to a straight substrate

step. Measurement of the LDOS ρ

at the surface by means of measur-

ing the differential conductance dI/dV is affected by local variations of

the tip–sample distance z and therefore does not exactly represent ρ

(Crommie et al., 1993b; Heller et al., 1994; Hormandinger, 1994). As a

consequence, the surface state dispersion E(k) determined from dI/dV

maps deviates somewhat from photoemission spectroscopy results

(Hormandinger, 1994). Simultaneous measurements of z and dI/dV

Figure 17–12. Surface

states conﬁ ned by two

parallel steps on Ag(111)

Atomically resolved

STM constant current

images at 4.8 K, 20 nm ×

12 nm, I = 1.8 nA at (a)

+21 mV and (b) +6 mV

showing standing-wave

patterns. (c and d) Cross

sections along the black

arrows in (a) and (b),

respectively, showing

the atomic corrugation

superimposed on the

standing waves. The

solid curves are the cal-

culated ILDOS. (From

Pivetta et al., 2003.)

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1087

have been used to recover the oscillating LDOS on a close-packed

Ag(111) surface at T = 50 K (Li et al., 1997).

A dependence of dI/dV on local z variations follows from Eq. (3). If

the second term in Eq. (3) is neglected, the differential conductance is

proportional to the product of ρ

and T. The exponential z-dependence

of T causes an error in the measurement of ρ

in terms of dI/dV, if the

tip–sample distance is not constant, but instead is controlled in con-

stant current mode at the same bias voltage where dI/dV is

measured.

At low bias, the tunneling current results from an integration over

a narrow energy window and consequently the standing wave oscil-

lations in the ILDOS get more pronounced (less k values contribute to

the pattern). This causes an oscillation of z, since at every position x,

the tip height z(x) is adjusted by the feedback loop to follow the ILDOS

oscillations at the preset constant-current value. Then the simultane-

Figure 17–13. Bias-dependent evolution of the LDOS and ILDOS oscillations

of surface states conﬁ ned by parallel surface steps. (a) Simultaneously recorded

constant current (gray shaded) and dI/dV (curves above) cross sections from

a quantum box of width L = 21.8 nm formed by two parallel steps on Ag(111)

Bias voltages (mV) are indicated (bias applied to the sample). (b) Calculated

electron density (gray shaded) and dI/dV. Note the difference between dI/dV

(LDOS) (three maxima) and topography (ILDOS) (ﬁ ve maxima) at −48 mV, a

bias voltage that might be considered to be close to E

. (From Pivetta et al.,

2003.)

1088 U. Weierstall

ously measured dI/dV signal does not reﬂ ect ρ

anymore, because the

z adjustments inﬂ uence the barrier transmission T, which depends

exponentially on z. Since dI/dV is proportional to the product of ρ

and

T, ρ

at E = eV can be recovered from dI/dV by division with T, which

is measured by measuring z(x), i.e., a constant-current image. With

these corrections, good agreement between LT-STM-derived disper-

sion curves E(k) and PES-derived dispersion curves has been achieved

(Li et al., 1997).

Another solution to avoid convolution between standing waves in

the tip height z of the constant-current line scan and those in the simul-

taneously recorded dI/dV spectra is to control z at a large negative bias

voltage (relative to the sample). Under these conditions, the current I

contains contributions from electronic states with many different oscil-

lation periods (k

values), which minimizes the standing waves in the

z signal (ILDOS). Thus the tip moves to a good approximation parallel

to the surface plane, unaffected by interference patterns in the LDOS.

The differential conductance is then roughly proportional to the LDOS

of the sample (Hormandinger, 1994). Such a measurement has been

published by Jeandupeux et al. (1999), and the result is shown in Figure

17–14. The upper graph displays the constant-current line scan on

which the tip was moved while taking differential conductance maps.

It can be seen that at a bias voltage of V = 0.3 V the tip–surface distance

is almost unaffected by standing waves and follows the real topogra-

phy. The differential conductance data are represented by gray levels

as a function of the distance x from the step edge and the energy E.

This plot already illustrates the dispersion of the Ag(111) surface state:

from top to bottom the wavelength of the LDOS oscillations increases

until it diverges at the band edge at E

= −65 meV. Analyzing constant

energy cuts of the differential conductance plot in Figure 17–14 in

quantitative terms by modeling the reﬂ ection of electrons at a potential

barrier with a reﬂ ected amplitude and a phase shift leads to values for

the wave number k for each energy, and thus the energy dispersion

relation E(k) of the Ag(111) surface state, which is shown in Figure 17–

15. The data were in excellent agreement with other STS-derived data

(Li et al., 1997) and PES data (Paniago et al., 1995).

The previously shown measurements of the dispersion relation on

noble metal surfaces were limited to k

vectors around the center of

the surface Brillouin zone (SBZ) and it has been found that in this limit

the surface state is free electron like, i.e., has an isotropic parabolic

dispersion. LT-STS measurements on Ag(111) and Cu(111) over an

extended energy range have shown a signiﬁ cant deviation from free

electron behavior for large k

vectors approaching the symmetry points

at the SBZ boundary (Burgi et al., 2000b).

Direct visualization of the surface state dispersion on Ag(110) by

means of Fourier transformation of differential conductance data taken

with an LT-STM at 4 K at energies up to the vacuum level has also been

shown (Pascual et al., 2001b). Low temperatures (4 K) enabled the nec-

essary high (2 meV) energy resolution and high stability to allow long

recording times for the measurement of the differential conductance

(dI/dV) using lock-in ampliﬁ cation techniques.

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1089

Figure 17–16a shows the LDOS oscillations in front of a step on

Ag(110) represented by a gray scale, plotted as a function of the dis-

tance form the step edge and the energy. Figure 17–16b shows the one-

dimensional Fourier transform of the spatial one-dimensional

conductance proﬁ les in Figure 17–16a and visualizes the dispersion of

the surface state in reciprocal space. A calculation shown in Figure

17–16c and d with a Bloch wave function limited to the ﬁ rst-order terms

(G = −1,0,1) could explain the features of Figure 17–16a and b. It could

100 2000

–1

–2

200

100

–100

1.1

1.0

0.9

0 100 200

x [Å]

dI/dV

[arb. units]

E [meV]

z [Å]

Figure 17–14. LDOS oscillations on Ag(111) at 5 K represented as gray levels

as a function of the lateral distance from the step x and of bias energy E = eV

with respect to E

. The upper graph shows the constant-current line scan (V

= 0.3 V, I = 2.0 nA) on which the STM tip was moved while taking the dI/dV

spectra. The lower graph is a cut of the dI/dV plot taken along the white line

at E = 148 meV (dots), and the line is a ﬁ t to theory. (From Jeandupeux et al.,

1999.)