Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

1070

Low-Temperature Scanning

Tunneling Microscopy

Uwe Weierstall

1 Introduction

The scanning tunneling microscope (STM) has revolutionized surface

science since its invention in 1982 (Binnig and Rohrer, 1982) by provid-

ing a means to directly image atomic scale spatial and electronic

structure. Using the combination of a coarse approach and piezoelec-

tric transducers, a sharp, metallic tip is brought into close proximity

with the sample. The distance between tip and sample is less than

1 nm, which means that the electron wave functions of tip and sample

start to overlap. A bias voltage is applied between tip and sample that

causes electrons to tunnel through the barrier. The tunneling current

is a quantum mechanical effect: tunneling of electrons can occur

between two electrodes separated by a thin insulator or a vacuum

gap and the tunneling current decays on the length scale of one

atomic radius. The tunneling current is in the range of picoamperes

to nanoamperes and is measured with a preampliﬁ er. In an STM, the

tip is scanned over the surface and electrons tunnel from the very

last atom of the tip apex to single atoms on the surface, providing

atomic resolution. The exponential dependence of the tunneling

current on the tip–sample distance can be exploited to control the

tip–sample distance with high precision. There are four basic opera-

tion modes for any STM: constant current imaging, constant height

imaging, spectroscopic imaging, and local spectroscopy. Their inter-

pretation and realization will be brieﬂ y discussed below. For details

about other modes and a comprehensive introduction to electron tun-

neling and STM see Wiesendanger (1994).

To acquire constant current images, a feedback loop adjusts

the height of the tip during scanning so that the tunneling current

ﬂ owing between tip and sample is kept constant. The height z is

adjusted by applying an appropriate voltage V

to the z-piezoelectric

drive while the lateral tip position (x,y) is determined by the

corresponding voltages applied to the x and y piezoelectric drives.

The recorded signal V

can be translated into a topography z(x,y)

if the sensitivity of the piezoelectric drives is known. The word

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1071

topography should be used with caution: since the local density of

states at the Fermi level is measured, a molecule adsorbed on a metal

surface that reduces the local density of states and may actually be

imaged as a depression.

To acquire constant height images, the feedback loop is switched off,

i.e., the tip is scanned at constant height above the surface, and varia-

tions in the current are measured. This mode has the advantage that

the ﬁ nite response time of the feedback loop does not limit the scan

speed. It can be used to collect images at video rates, offering the

opportunity to observe dynamic processes at surfaces. However,

thermal drift limits the time of the experiment and there is an increased

risk of crashing the tip.

To measure differential conductance (dI/dV) maps with the STM, a

high-frequency sinusoidal modulation voltage is superimposed on the

constant dc bias voltage V

bias

between tip and sample. The modulation

frequency is chosen higher than the cutoff frequency of the feedback

loop, which keeps the tunneling current constant. By recording the

tunneling current modulation, which is in phase with the applied bias

voltage modulation, with a lock in ampliﬁ er, a spatially resolved spec-

troscopic signal dI/dV|

bias

can be obtained simultaneously with the

constant current image (Binnig et al., 1985a,b).

By measuring the differential conductance dI/dV at a ﬁ xed tip posi-

tion with open feedback loop (constant tip–sample distance z) while

sweeping the applied bias voltage, an energy-resolved spectrum can

be obtained. This is useful for probing, e.g., band-gap states in semi-

conductors or the onset of surface states on metals.

The tunneling current I at a given tip position is approximately equal

to the integrated local density of states (ILDOS), integrated over the

energy range between the Fermi energy E

of the sample and eV, where

V is the applied bias voltage. Therefore the differential conductance

dI/dV is approximately proportional to the local density of states

(LDOS) of the sample at the energy eV, and a constant current image

should represent a contour of constant ILDOS. For measurements close

to E

, i.e., at low bias voltages, the LDOS and ILDOS are essentially the

same and a constant current image at low bias (a few millivolts) is

therefore approximately proportional to the sample LDOS at the Fermi

energy E

(assuming the tip has a uniform density of states and the

temperature is low). To illustrate how to arrive at the picture presented

above, the theoretical treatment of electron tunneling is brieﬂ y

outlined.

A one-dimensional WKB approximation predicts that the tunneling

current at low temperatures (where the Fermi distribution is a step

function) is given by

IExeVExTEeVxdE

(

)

−+

(

)

(

)

∫

ρρ

,,,,

(1)

where ρ

(E) and ρ

(E) are the density of states of the sample and the tip

at the location x and energy E, measured with respect to their individ-

ual Fermi levels, and V is the applied bias voltage (Hamers, 1989). The

1072 U. Weierstall

tunneling transmission probability T(E,eV,x) for electrons with energy

E and applied voltage V is given by

TEeVx zx

eV E,,

(

)

=−

(

)

++ −

(

)













exp



φφ (2)

where φ

and φ

are the work functions of sample and tip and z is the

tip–sample distance. Therefore, assuming that the tip electronic struc-

ture is featureless, Eq. (1) shows that the tunneling current at position

x is approximately equal to the ILDOS of the sample integrated between

and eV, weighted by the transmission probability T. Examination of

Eq. (2) shows that if eV < 0 (i.e., negative sample bias), the transmission

probability is largest for E = 0 (corresponding to electrons at the Fermi

level of the sample). If eV > 0 (positive sample bias) the probability is

largest for E = eV (corresponding to electrons at the Fermi level of the

tip). Therefore the tunneling probability is always largest for electrons

at the Fermi level of whichever electrode is negatively biased. This is

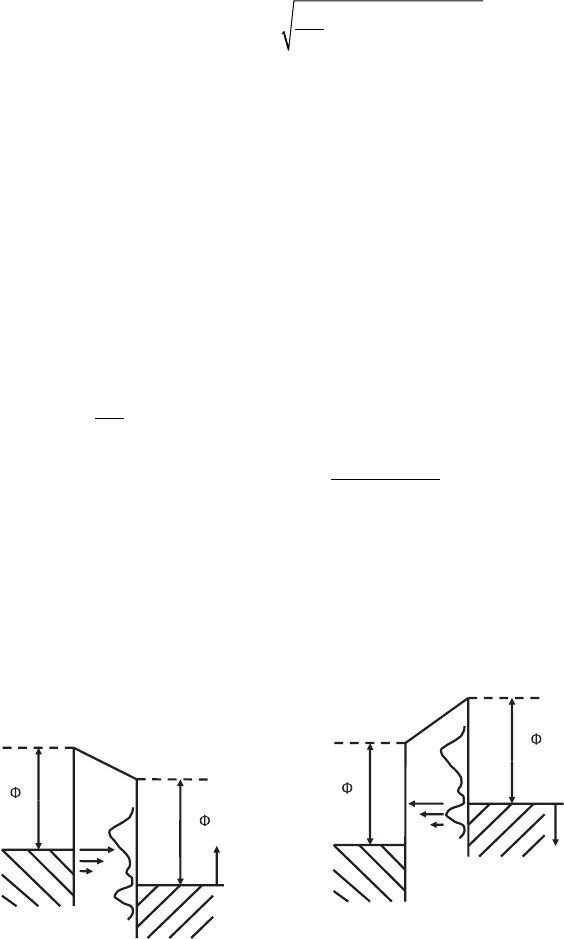
shown schematically in Figure 17–1.

Differentiating Eq. (1) gives the differential conductance

eV x x T eV eV x

Ex E e

∝

(

)

(

)

(

)

(

)

−

ρρ

,, ,,

VVx

dT E eV x

(

)

(

)

∫

(3)

The ﬁ rst term is the product of the density of states of the sample,

the density of states of the tip, and the tunneling transmission pro-

bability. The second term contains the voltage dependence of the

tunneling transmission probability. Since T is a smooth monotonically

Figure 17–1. Energy level diagram of sample and tip with V being the sample

voltage relative to the tip. Left: electrons tunneling from tip to sample with

positive sample bias voltage. Right: electrons tunneling from sample to tip

with negative sample bias voltage. The curve represents the density of states

of the sample; the tip density of states is assumed featureless. The different

lengths of the arrows illustrate the fact that the tunneling probability is largest

for electrons at the Fermi level of the negatively biased electrode. Φ

and Φ

are

the tip and sample work functions.

eV>0 eV<0

sample

tip sample tip

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1073

increasing function of V, structure in dI/dV can be assigned to changes

in the sample LDOS at eV, assuming a tip with featureless density of

states.

In general, however, the tip electronic structure is unknown and may

not be featureless. The small size of the STM tip is expected to signiﬁ -

cantly modify its electronic structure from that of a bulk material.

Therefore, it is usually necessary to compare tunneling spectra acquired

at different locations on the surface to distinguish the spatially invari-

ant contribution of the tip and the spatially varying contribution from

the sample. Comparing spectra taken with different tips also helps to

eliminate tip contributions.

At ﬁ nite temperatures Eq. (1) contains an additional Fermi distribu-

tion factor, which imposes a limit on spectroscopic resolution. At room

temperature, with k

T ≈ 0.026 eV, the spread of the tip and sample

energy distribution are each 2 k

T ≈ 0.052 eV. Therefore the total spread

is ∆E ≈ 4 k

T ≈ 0.1 eV. To make high-resolution spectroscopic measure-

ments with ∆E in the millielectron volt range, experiments must be

conducted at cryogenic temperatures.

To work with clean metal and semiconductor surfaces, STM mea-

surements have to be done in ultrahigh vacuum (UHV). Operating a

UHV-STM at cryogenic temperature has several major advantages:

1. Close coupling of the microscope to a large temperature bath that

keeps constant temperature over hours or days ensures a reduction of

thermal drift and allows long-term measurements. The reduction of

thermal drift during low-temperature operation is further improved

by the fact that the thermal expansion coefﬁ cients at liquid helium

temperature are two or more orders of magnitude smaller than at room

temperature.

2. Superior vacuum conditions: If the microscope is incorporated in

a cryostat that acts as an effective cryopump, surfaces are kept free

from contamination over days.

3. Thermal diffusion of adsorbates and defects is suppressed—stable

imaging becomes possible even for weakly bound species. Moreover,

low temperatures might also stabilize the atomic conﬁ guration at the

tip end by preventing sudden jumps of the most loosely bound fore-

most atoms due to thermal activation.

4. Small thermal broadening at the Fermi energy is a necessary

condition for spectroscopic investigations with high-energy

resolution.

5. Individual adsorbates can be manipulated with the STM to quali-

tatively probe their interaction with the substrate.

6. Physical properties can be studied as a function of temperature

or physical effects can be examined that occur only at low temperatures

(e.g., superconductivity, Kondo effect, nanoscale magnetism).

7. Piezo non l i nea rit ies and hysteresis (creep) affecting the piezoelec-

tric scanners of the STM decrease substantially at low temperatures.

In an effort to improve the stability of the microscope and the atoms

or molecules under investigation, a variety of low-temperature UHV

STM designs have been developed.

1074 U. Weierstall

2 Design Principals

All low-temperature STMs (LT-STM) operate in UHV, which is a pre-

requisite for obtaining a clean surface. To reach a low ﬁ nal tempera-

ture and a short cooling time, the thermal conductivity from the

microscope to the cryogen has to be maximized, and the thermal load

from room temperature has to be minimized. Heat transfer through

the electrical connections and contacts has to be considered as well

as thermal radiation. The discussion here is restricted to liquid

helium (LHe)-cooled instruments. In designing an LT-STM, there is a

choice between a ﬂ ow cryostat and a bath cryostat to cool the STM.

Then there are two basic designs: one in which only the sample is

cooled and one in which the whole STM is cooled and surrounded by

a radiation shield.

2.1 STM with LHe Continuous-Flow Cryostat

If the ability to change temperature on a relatively short time scale is

of importance, the heat reservoir should be small. Therefore in

variable-temperature STMs that can work from room temperature

down to liquid helium temperature, a ﬂ ow cryostat is usually used and

only the sample is cooled to ensure a small thermal mass. The sample

is thermally connected to the cryostat via a ﬂ exible Cu or Au braid.

Cryostat vibrations and instabilities caused by boiling of the coolant

as well as different thermal expansion coefﬁ cients of various materials

during temperature cycling require special attention. To reduce the

amplitude of vibrations introduced by the cryostat, it is important to

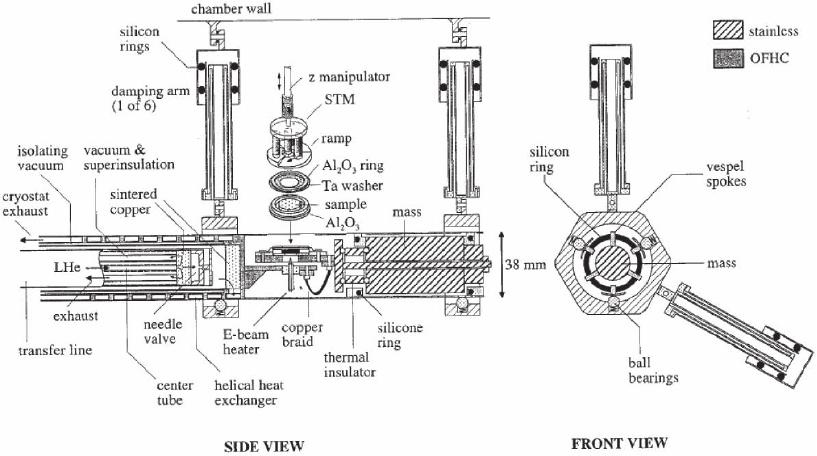
mechanically decouple the braid to a heavy mass (Bott et al., 1995) (see

Figure 17–2). Since only the sample is cooled, the scanner has to be

thermally isolated from the sample to avoid heat transfer to the sample.

One advantage of this approach for variable-temperature operation is

that the repeated recalibrations of the STM made necessary by tem-

perature-dependent changes in the piezo coefﬁ cients are avoided. But

large thermal gradients can create image drift problems and possible

disturbances due to heat transfer from the “hot” tip scanning the cold

sample (Xu et al., 1994).

An example of a variable-temperature STM with ﬂ ow cryostat cooling

the sample only is shown in Figure 17–3 (Behler et al., 1997). Other

examples are given in Bott et al. (1995), Horch et al. (1994), and Petersen

et al. (2001).

LHe ﬂ ow cryostats can also be used to cool the entire STM. This

results in improved thermal stability due to thermal equilibrium

between all STM parts. If fast cooldown times are required, the STM

can be connected rigidly to the cold end of the ﬂ ow cryostat (Mugele

et al., 1998; Zhang et al., 2001). This mandates a high mechanical stabil-

ity (high resonance frequency) of the STM so that the vibration fre-

quencies caused by the He ﬂ ow are well below the eigenfrequency of

the STM. The microscope is surrounded by one or two radiation shields.

Higher mechanical stability can be obtained if the STM is suspended

with springs inside a radiation shield to provide vibration isolation

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1075

kryostat

sample

holder

sample

block

copper

braid

viton

manipulator

fixing screws

teflon

rigid tube

catched braid

viton

second mass

a’)

b) b’)

c) c’)

2 kHz

kHz

arb.units

Figure 17–2. Mechanical decoupling of a copper braid connecting a ﬂ ow

cryostat and a sample holder. Shown are modiﬁ cations and their effect on the

noise spectrum. (a) Initial arrangement of the sample holder connected to the

cryostat by a copper braid. (a′) Fourier spectrum of the tunneling current with

noise showing up as peaks. (b) Resonance frequencies of cryostat are increased

by deﬁ ning nodes with a rigid tube mounted on the cryostat with three screws

separated by 120° at each node. (b′) Fourier spectrum after modiﬁ cation; noise

frequencies are shifted to higher frequencies. (c) Noise from the copper braid

coupling is damped out by ﬁ xing the copper braid thermally isolated to a

massive block. (c′) Noise is greatly reduced. (From Bott et al., 1995.)

1076 U. Weierstall

from the cryostat (Wolkow, 1995; Stipe et al., 1999b) (see Figures 17–4

and 17–5).

2.2 STM with LHe Bath Cryostat

A bath cryostat is usually used if the whole STM is being cooled. The

bath cryostat serves as a large thermal reservoir that is being cooled

down prior to the measurements. This approach has been successfully

applied on a number of 4 K microscopes (Eigler and Schweizer, 1990;

Gaisch et al., 1992; Stranick et al., 1994b; Rust et al., 1997; Meyer, 1996;

Becker et al., 1998; Ferris et al., 1998; Harrell and First, 1999; Stroscio,

2000). If all parts of the system are allowed to reach thermal equilib-

rium, thermal drift may be virtually eliminated. Bath cryostat low-

temperature STMs operating in a rotatable magnetic ﬁ eld have also

been built (Wittneven et al., 1997); some of them are

He refrigerated

and operate at about 250 mK (Pan et al., 1999; Kugler et al., 2000; Matsui

et al., 2003). Sample turnaround times for the very-low-temperature

variants are quite long since it can take 36 h to reach thermal equilib-

rium (Pan et al., 1999). LT-STMs with bath cryostats are difﬁ cult to use

for variable temperature measurements, e.g., study of diffusion and

phase transitions, since they use a large cold reservoir to cool the STM

and the temperature cannot be changed easily. Temperature control by

altering the exchange gas pressure in combination with a PID-

controlled heater has been achieved (Rust et al., 2001). Another way

to achieve measurements at different temperatures is to simply remove

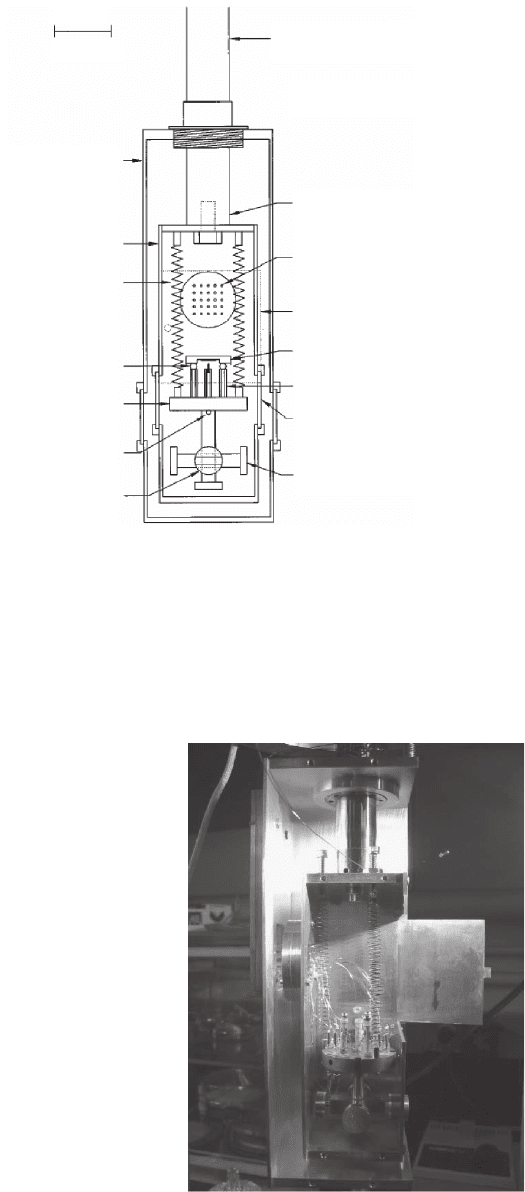
Figure 17–3. Example of a variable-temperature STM for operation in the temperature range of 20–

300 K. Only the sample is cooled. Continuous ﬂ ow cryostat on the left; arrows show helium ﬂ ow. The

sample is thermally connected to the cryostat by a copper braid and mechanically decoupled with a

heavy stainless steel mass supported by O-rings. (From Behler et al., 1997.)

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1077

Continuous Flow

L–He/N

Cryostat

Sample at

8 K to 350 K

Cold Tip

Electrical

Feedthroughs

Inner

Access Door

Mo Sample

Holder

Piezotubes (4)

Sapphire

Laser Window

Samariam-

Cobalt Magnets

Inner Shield

Inconel

Springs (3)

W Balls (3)

and Tip

Mo Base Plate

Hole for

Dosing

Clamping

Screw

Outer Shield

Scale

2.5 cm

Figure 17–4. A variable-temperature scanning tunneling microscope cooled

with a continuous-ﬂ ow cryostat. The STM and the sample are suspended from

three springs that provide the second stage of vibrational isolation. The design

allows for in situ dosing and irradiation of the sample as well as the exchange

of samples and tips. (From Stipe et al., 1999b.)

Figure 17–5. Low and variable

temperature STM in the author’s

laboratory, which is very similar

in design to the one by Stipe et

al. (1999b). Refer to Figure 17–4

for identiﬁ cation of different

parts. The front of the outer radi-

ation shield and the sides of both

radiation shields are missing to

enable the inside to be viewed.

1078 U. Weierstall

liquid helium from the cryostat, giving rise to a temperature increase

of the microscope over days, thus enabling drift-free STM measure-

ments at well-deﬁ ned temperatures up to 300 K. (Jeandupeux et al.,

1999)

Since the tunneling current has an exponential dependence on the

distance between tip and sample, vibrations can cause strong noise.

Therefore the construction of the STM scanner, consisting of tip holder,

sample holder, and actuators, should be as rigid as possible to increase

the mechanical eigenfrequency of the scanner. For typical tube scanner

setups this eigenfrequency lies in the range of 1–10 kHz. A two-stage

damping system consisting of an external damper (e.g., air damped

feet suspension of the whole UHV chamber) and an internal damper

(e.g., scanner suspended on springs and damped by eddy current

dampers) effectively isolates the tunneling gap from building vibra-

tions and acoustic noise. The two damping stages should have reso-

nance frequencies well below building and acoustic frequencies and

should be strongly damped (low Q-factor).

With a low-temperature STM the boiling cryogenic liquid produces

additional vibrations after the ﬁ rst damping stage. Even worse, the

boiling liquid has to be in close proximity to the vibration-sensitive

scanner to enable good thermal contact to the scanner. Therefore there

are two contradictory demands for the design of a low-temperature

STM: mechanical decoupling of the STM head and thermal coupling

to the cryostat.

This problem has been solved by different groups in different ways

and in the following we will discuss three design examples. They all

have in common a helium bath cryostat surrounded by a liquid nitro-

gen cryostat, which acts as a radiation shield. They all have a two-stage

damping system; in the ﬁ rst stage the whole UHV chamber is mechani-

cally decoupled from the ﬂ oor by pneumatic dampers. The designs

differ in the way the second damping stage is realized (see Figure

17–6):

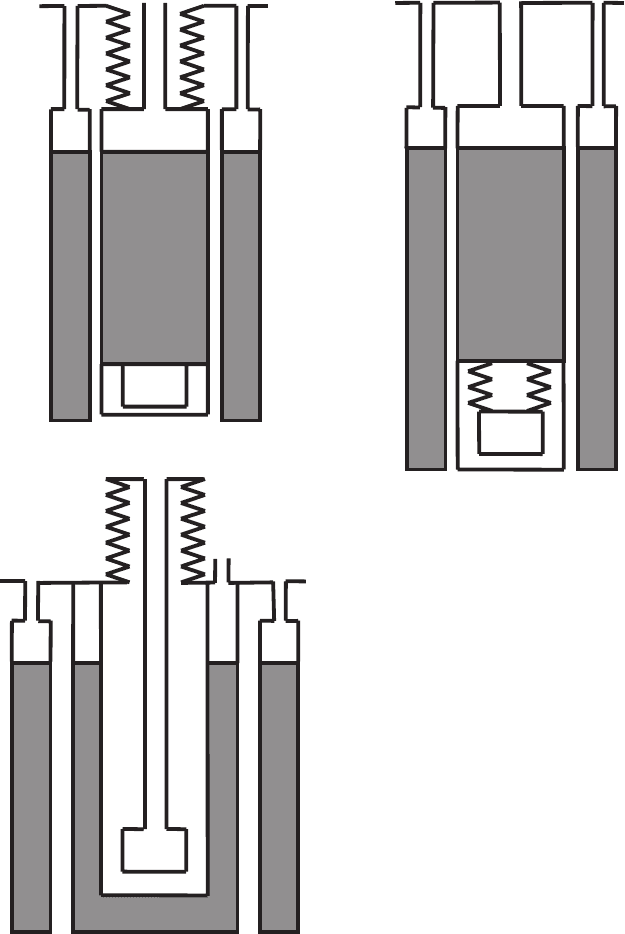
The IBM-Rueschlikon/University Lausanne LT-STM designed by R.

Gaisch (Gaisch et al., 1992) uses a bellow to mechanically decouple the

liquid helium cryostat from the liquid nitrogen cryostat and the UHV

chamber. The STM, however, is rigidly connected to the liquid helium

cryostat, which results in very effective cooling. However, vibrations

from the cryostat can reach the STM unattenuated.

The LT-STM designed by G. Meyer and K.H. Rieder (Meyer, 1996)

has no damping between the liquid helium and the liquid nitrogen

cryostat; instead the STM is suspended from the He cryostat by small

extension springs and thereby is mechanically decoupled during mea-

surements. During cooldown the STM is lowered onto a copper plate

connected to the He cryostat to achieve good thermal contact. Since the

thin springs are not very good thermal conductors, the STM has to be

effectively shielded against incoming thermal radiation. This is

achieved by a two-stage radiation shield with the inner shield con-

nected to the He bath and the outer shield connected to the liquid

nitrogen bath. The STM is then almost thermally isolated during mea-

surements (see Figure 17–7).

Chapter 17 Low-Temperature Scanning Tunneling Microscopy 1079

LHe

STM

LHe

Figure 17–6. Schematic comparison of different LT-STMs with bath cryostat.

(A) R. Gaisch/IBM Rueschlikon, (B) G. Meyer/FU Berlin, (C) D. Eigler/IBM

Almaden. The connection to the LHe cryostat and the second damping stage

of the STM is shown. (A) and (B) have a cryoshield surrounding the STM.

In (A) the LHe cryostat is decoupled from the LN

cryostat by bellows. In (B)

the STM is decoupled from the LHe cryostat by springs. In (C) the STM is

decoupled from the LHe cryostat by a bellows-supported pendulum. Thermal

contact is made by He exchange gas surrounding the evacuated pendulum.