Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


32.4 Continuous Random Variable 803
where h
α
(x) is a function of all x’s except x
α
. By multiplying it by a constant,
we can always choose g(x
α
) in such a way that
#
∞
−∞
g(x
α
) dx
α
=1. (32.51)
Then since
1=
##
Ω
f(x) d
m
x =
#
∞
−∞
g(x
α
) dx
α
##
Ω
h
α
(x) d
m−1
x,
where Ω
is the region of integration of the remaining variables, we also have
##
Ω
h
α
(x) d
m−1
x =1.
From this we conclude that the average of any function depending on x
α
alone
can be calculated using not the whole density f(x), but g(x
α
). In particular,
X
α
=
#
∞
−∞
x
α
g(x
α
) dx
α
,σ
2
(X
α
)=
#
∞
−∞
(x
α
−X
α
)
2
g(x
α
) dx
α
.
(32.52)
Define cov(X
α
,X
β
), the covariance of x
α
and x
β
, for a general density Covariance defined
function f(x), by
cov(X
α
,X
β
) ≡
##
Ω
(x
α
−X
α
)(x
β
−X
β
)f(x) d
m
x
≡(X
α
−X
α
)(X
β
−X
β
), (32.53)
and note that by (32.49),
cov(X
α
,X
α
)=σ
2
(X
α
), cov(X
β
,X
β
)=σ
2
(X
β
). (32.54)
Now suppose that x
α
is independent of the rest of the variables and β = α.
Then
cov(X
α
,X
β
)=
#
∞
−∞
(x
α
−X
α
)g(x
α
) dx
α
##
Ω
(x
β
−X
β
)h
α
(x) d
m−1
x =0.
The result follows from the fact that the integration over Ω
is a constant and
the integral over x
α
can be done independently:
#
∞
−∞
(x
α
−X
α
)g(x
α
) dx
α
=
#
∞
−∞
x
α
g(x
α
) dx
α
=X
α
by (32.52)
−X
α
#
∞
−∞
g(x
α
) dx
α
=1 by (32.51)
=0.
The preceding discussion shows that cov(X
α
,X
β
)measureshowmuchx
α
is independent of the rest of the variables. If it is, then cov(X
α
,X
β
)=0;if
it is not, then cov(X
α
,X
β
) = 0. A quantity related to cov(X
α
,X
β
), called Correlation
defined
correlation,is

804 Probability Theory
cor(X
α
,X
β
)=
cov(X
α
,X
β
)
σ(X
α
)σ(X
β
)
. (32.55)
The “strongest” correlation occurs when α = β,inwhichcase
cor(X
α
,X
α
)=
cov(X
α
,X
α
)
σ
2
(X
α
)
= 1 by (32.54).
The “weakest” correlation occurs when α = β and x
α
is independent of the
rest of the variables, in which case cor(X
α
,X
β
) = 0. Thus, cor(X
α
,X
β
)
indeed measures how much x
α
and x
β
are correlated. Problem (32.22) shows
that |cor(X
α
,X
β
|≤1.
32.4.1 Transformation of Variables
Sometimes it is necessary or convenient to change a given set of random
variables to another set. Suppose that x = {x
i
}
m
i=1
is a set of variables, and
u = {u
i
}
m
i=1
are new variables of which the x
i
are functions. Given a density
f(x), the probability of finding x in an infinitesimal volume d
m
x is f (x)d
m
x.
What is the corresponding probability in terms of the u variables? What is
the probability density g(u)sothatg(u)d
m
u is the probability that u lies in
the infinitesimal volume d
m
u?Theansweris
g(u)=f
x
1
(u),x
2
(u),...,x
m
(u)
!
J(x, u), (32.56)
where J(x, u) is the Jacobian of the x-to-u transformation, whose special cases
in two and three dimensions were given in (6.65) and (6.66). Equation (32.56)
is obtained from f (x)d
m
x by writing x’s in terms of u’s, keeping in mind that
d
m
x = J(x, u)d
m
u.
In most cases, there are only two variables x and y, which are transformed
into u and v. Then (32.56) yields
g(u, v)=f
x(u, v),y(u, v)
!
∂x
∂u
∂y
∂u
∂x
∂v
∂y
∂v
. (32.57)
Example 32.4.2.
The random variables x and y have the density function
f(x, y)=
0
c(x + y)e
−x
if 0 <x,0<y<1;
0otherwise,
(32.58)
where c is a positive constant. What is the density function h(u)forthesum
u = x + y?
As will become clear below, it is convenient to write f(x, y) in terms of the θ
function introduced in Section 5.1.3 Equation (5.18):
f(x, y)=cθ(x)θ(y)θ(1 − y)(x + y)e
−x
. (32.59)

32.4 Continuous Random Variable 805
The reader is urged to verify that this is identical to (32.58). Let x = v.Then
u = x + y gives y = u −v, and the Jacobian for the transformation is
∂x
∂u
∂y
∂u
∂x
∂v
∂y
∂v
=
01
1 −1
=1. (32.60)
Therefore, all is needed is to replace x and y in f(x, y):
g(u, v)=cθ(v)θ(u − v)θ(1 − u + v)ue
−v
.
This is the convenience we mentioned above: we don’t have to worry about different
cases corresponding to different limits of u and v;theθ function automatically takes
care of that!
To find h(u), we need—by definition—to integrate over all values of v.Because
of the last θ factor in g(u, v), we need to consider two cases: 0 <u<1andu>1. In
the first case, θ(1 −u + v)=1becausethefirstθ function requires v to be positive.
Then the middle θ function sets the upper limit of v integration to u.Hence,
h(u) ≡
#
∞
−∞
g(u, v) dv =
#
u
0
cue
−v
dv = cu
1 − e
−u
!
, 0 <u<1.
In the second case, θ(1−u+v)requiresv to be grater than u−1, and the middle
θ function still sets the upper limit of v integration to u. Therefore,
h(u)=
#
u
u−1
cue
−v
dv = −cu e
−v
u
u−1
= cue
−u
(e − 1),u>1.
The two cases can be combined using the θ function:
h(u)=cu
.
θ(u)θ(1 − u)
1 − e
−u
!
+ θ(u − 1)e
−u
(e − 1)
/
.
Suppose that x and y are independent random variables with the density
function
f(x, y)=f
1
(x)f
2
(y).
We want to find the density function h(u)oftheirsumu = x + y.Let
x = v and y = u − v, so that the sum is indeed x + y. The Jacobian of the
transformation is 1 by (32.60). Therefore, by (32.57),
g(u, v)=f
x(u, v),y(u, v)
!
= f
1
(v)f
2
(u − v).
The density function of each variable is obtained by integrating over the other
variable. Thus,
h(u) ≡
#
∞
−∞
g(u, v) dv =
#
∞
−∞
f
1
(v)f
2
(u − v) dv. (32.61)
The reader may recall from our discussion of Laplace transform that h is the
convolution of f
1
and f
2
.

806 Probability Theory
Example 32.4.3. Assume that x and y are independent variables with
f
1
(x)=
1
π(x
2
+1)
, −∞ <x<∞;
f
2
(y)=
1
π(y
2
+1)
, −∞ <y<∞.
Then their sum u = x + y has the density function
h(u)=
1
π
2
#
∞
−∞
dv
(v
2
+1)[(u − v)
2
+1]
=
2
π(u
2
+4)
, −∞ <u<∞
leaving the verification of the last integration for Problem 32.25.
32.4.2 Normal Distribution
One of the most frequently used probability distributions is Gauss’ normal
distribution given by
f(x)=
1
√
2πσ
e
−(x−m)
2
/2σ
2
, −∞ <x<∞. (32.62)
It can be easily shown that X = m and, as the notation suggests, the
variance is σ
2
.
To find the probability that x lies in the interval (a, b), we have to integrate
f(x)froma to b:
p(a<x<b)=
1
√
2πσ
#
b
a
e
−(x−m)
2
/2σ
2
dx.
Let y =(x − m)/
√
2 σ and substitute for x in terms of y.Then
p(a<x<b)=
1
√
π
#
b−m
√
2 σ
a−m
√
2 σ
e
−y
2
dy =
1
2
erf
b − m
√
2 σ
− erf
a −m
√
2 σ
,
(32.63)
where erf is the error function introduced in Equation (11.9). The error
function has been tabulated precisely because of its relation to the normal
distribution.
Suppose a and b are given in terms of their distance from the mean as a
multiple of the standard deviation: a = m + k
1
σ and b = m + k
2
σ,thenwe
have the important relation
p(m + k
1
σ<x<m+ k
2
σ)=
1
2
*
erf
k
2
/
√
2
− erf
k
1
/
√
2
+
. (32.64)
In particular, if k
1
= −k
2
≡−k,then
p(m −kσ<x<m+ kσ)=
1
2
*
erf
k/
√
2
− erf
−k/
√
2
+
. (32.65)
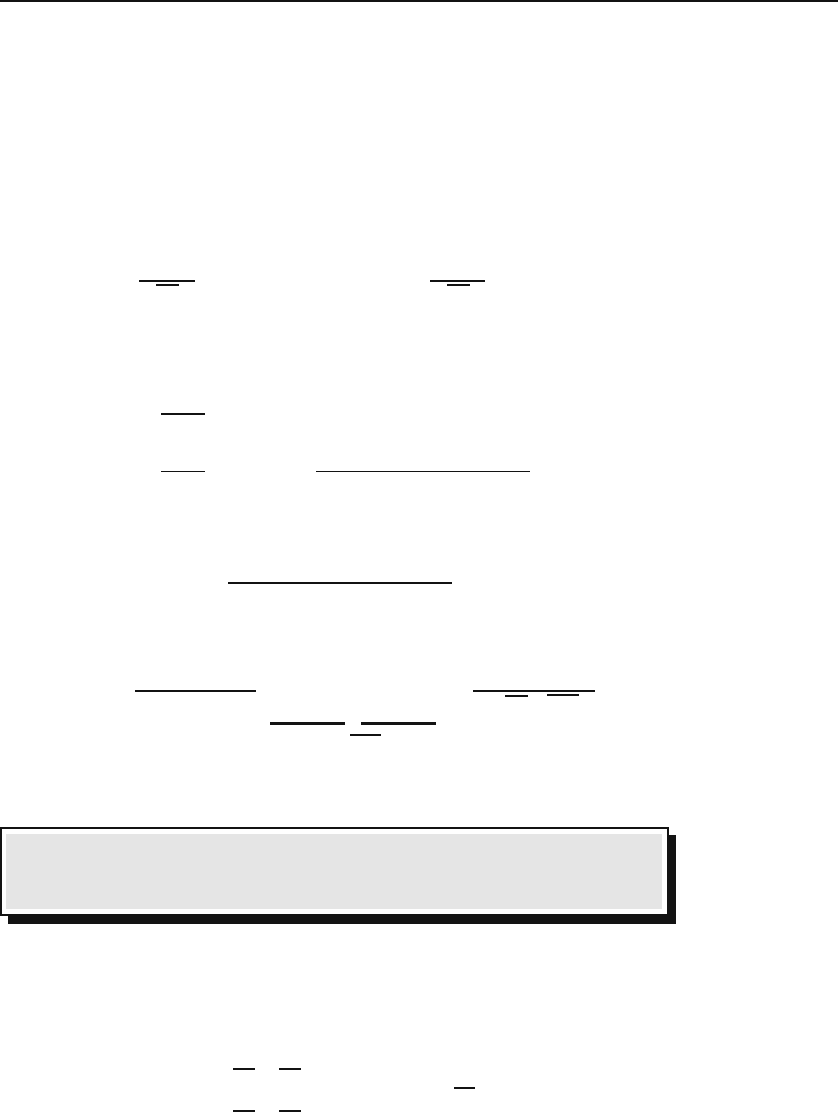
32.4 Continuous Random Variable 807
For k =1, 2, 3 this yields
p(m − σ<x<m+ σ)=0.6827
p(m − 2σ<x<m+2σ)=0.9545
p(m − 3σ<x<m+3σ)=0.9973.
Let x and y be random variables having the same normal distribution with
mean m and variance σ
2
f
1
(x)=
1
√
2πσ
e
−(x−m)
2
/2σ
2
,f
2
(y)=
1
√
2πσ
e
−(y−m)
2
/2σ
2
.
We want to find the distribution of the sum u = x + y. This is a special case
of (32.61). Therefore, we can immediately write
h(u)=
1
2πσ
2
#
∞
−∞
e
−(v− m)
2
/2σ
2
e
−(u−v−m)
2
/2σ
2
dv
=
1
2πσ
2
#
∞
−∞
exp
−
(v − m)
2
+(u − v − m)
2
2σ
2
dv.
The reader may verify that the exponent can be simplified to
−
(v − u/2)
2
+(u − 2m)
2
/4
σ
2
.
Substituting back in the integrand gives
h(u)=
e
−(u−2m)
2
/4σ
2
2πσ
2
#
∞
−∞
e
−(v− u/2)
2
/σ
2
dv
=
√
πσ
2
=
e
−(u−2m)
2
/4σ
2
√
2π
√
2σ
2
.
This shows that
Box 32.4.1. If the random variables x and y have the same normal dis-
tribution, then their sum has a normal distribution with twice the mean
and twice the variance.
Example 32.4.4. Let x and y be independent random variables whose density
functions f
1
and f
2
are normal distribution with m =0andσ = 1. What is the
density function h(u) for the ratio x/y?
Let x = v,theny = v/u makes u the sought-after ratio. The Jacobian of the
transformation is
J =
∂x
∂u
∂y
∂u
∂x
∂v
∂y
∂v
=
0 −v/u
2
11/u
=
|v|
u
2
.
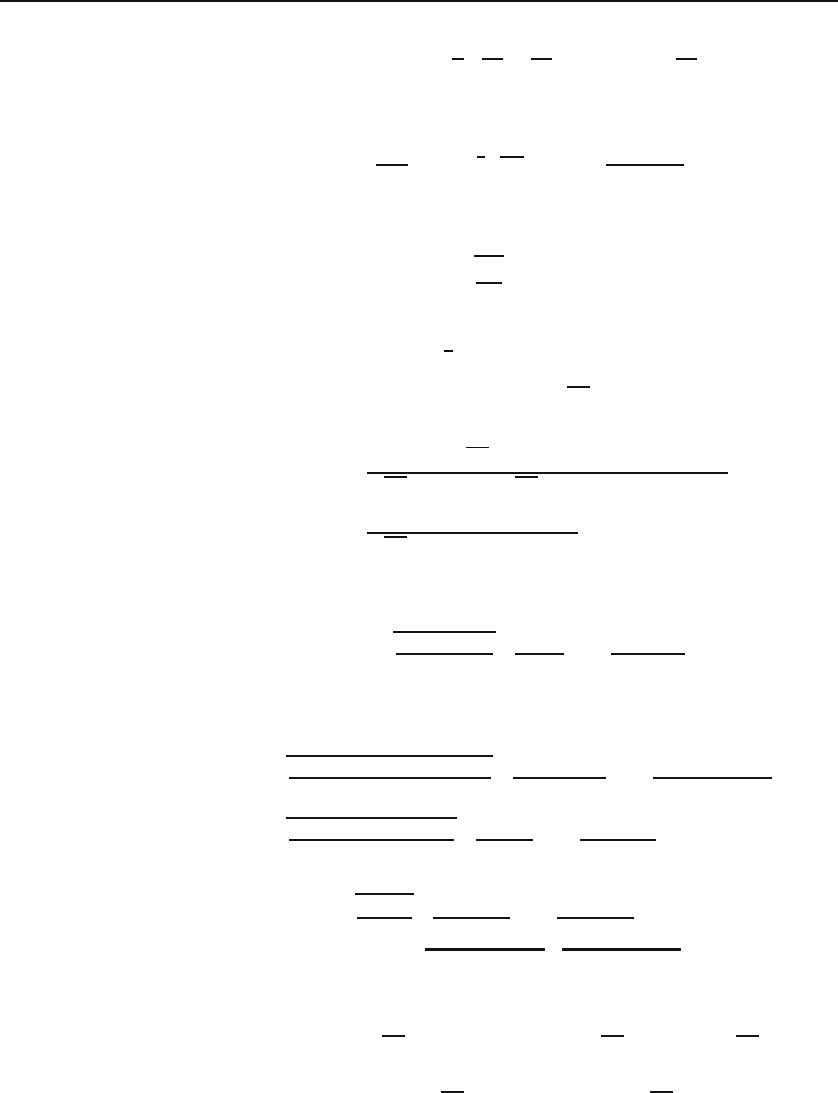
808 Probability Theory
Then
g(u, v)=f
1
(v)f
2
v
u
|v|
u
2
=
1
2π
e
−v
2
/2
e
−v
2
/2u
2
|v|
u
2
.
To find h(u)weintegrateg(u, v) over all values of v,namely−∞ to ∞.Since
the integrand is even, we can integrate from 0 to ∞ and multiply the result by 2.
Therefore,
h(u)=
1
πu
2
#
∞
0
e
−(
1
2
+
1
2u
2
)v
2
vdv=
1
π(u
2
+1)
.
The integration is straightforward as the reader can verify.
Equation (32.29), when written in the form (replacing m with x)
P (x, n)=
2
nπ
e
−(x−n/2)
2
/(n/2)
displays the similarity of the binomial distribution and the normal distribution
for the special case of p = q =
1
2
. The equation shows that the mean is n/2
and the variance n/4. We now generalize this to arbitrary p and q.
Using the Stirling approximation x! ≈
√
2πe
−x
x
x+1/2
and replacing m
with x, we write (32.27) as
P (x, n) ≈
√
2πe
−n
n
n+1/2
p
x
q
n−x
√
2πe
−x
x
x+1/2
√
2πe
−n+x
(n −x)
n−x+1/2
=
n
n+1/2
p
x
q
n−x
(n − x)
x
√
2πx
x+1/2
(n − x)
n+1/2
,
or, pulling out the power of 1/2 and collecting all terms with equal powers
together, we obtain
P (x, n) ≈
n
2πx(n −x)
nq
n −x
n
p(n −x)
xq
x
.
In the approximation we are seeking, we assume that x is close to the mean
np and write x = np + δ where δ is small compared to np.Thenweget
P (x, n) ≈
n
2π(np + δ)(n −np −δ)
nq
n − np − δ
n
p(n −np −δ)
(np + δ)q
np+δ
=
n
2π(np + δ)(nq − δ)
nq
nq − δ
n
npq − pδ
npq + qδ
np+δ
,
or
P (x, n) ≈
1
2πnpq
1
1 − δ/nq
n
1 − δ/nq
1+δ/np
np+δ
≡A
. (32.66)
To proceed, we take the log of the term we have designated as A:
ln A = −n ln
1 −
δ
nq
+(np + δ)
ln
1 −
δ
nq
− ln
1+
δ
np
=(−nq + δ)ln
1 −
δ
nq
− (np + δ)ln
1+
δ
np
.

32.5 Problems 809
Expanding the log terms up to the second order yields
ln A ≈ (−nq + δ)
−
δ
nq
−
δ
2
2n
2
q
2
− (np + δ)
δ
np
−
δ
2
2n
2
p
2
= −
δ
2
2nq
−
δ
2
2np
= −
δ
2
2n
1
q
+
1
p
= −
δ
2
2npq
⇒ A ≈ e
−
δ
2
2npq
.
Substituting this in (32.66) with δ = x −np,weobtain
P (x, n) ≈
1
2πnpq
e
−
(x−np)
2
2npq
,
which shows that P (x, n) is a normal distribution with mean np and variance
npq.
It can also be shown that the Poisson distribution (32.43) approaches the
normal distribution when n and λ are both large and δ = n − λ is small
compared to both:
p(n) →
1
√
2πλ
e
−(n−λ)
2
/2λ
.
We therefore have the law of large numbers:
law of large
numbers
Box 32.4.2. In the limit that the random variable and the mean go to
infinity, both the binomial and Poisson distributions approach the Gauss’
normal distribution.
Normal distribution is a remarkable density function. We just saw that
both binomial and Poisson distributions approach it in the limit of large n.
But it goes beyond these two distributions. In fact it can be shown that a
set of identically distributed random variables with an arbitrary distribution
is approximately normally distributed if the number of components is large
enough. This is the content of the central limit theorem,andtherea-
central limit
theorem
son that normal distribution is the distribution of choice in many statistical
applications.
32.5 Problems
32.1. Using Venn diagrams, show that the operation of union distributes over
intersection and vice versa:
A ∩ (B ∪ C)=(A ∩ B) ∪ (A ∩ C),
A ∪ (B ∩ C)=(A ∪ B) ∩ (A ∪ C).
32.2. Using Venn diagrams, show that
A ∩(B − C)=(A ∩ B) −(A ∩C),
A −(B ∪ C)=(A − B) −C.
810 Probability Theory
32.3. Using Venn diagrams, show that
(A ∪ B)
c
= A
c
∩ B
c
and (A ∩ B)
c
= A
c
∪ B
c
.
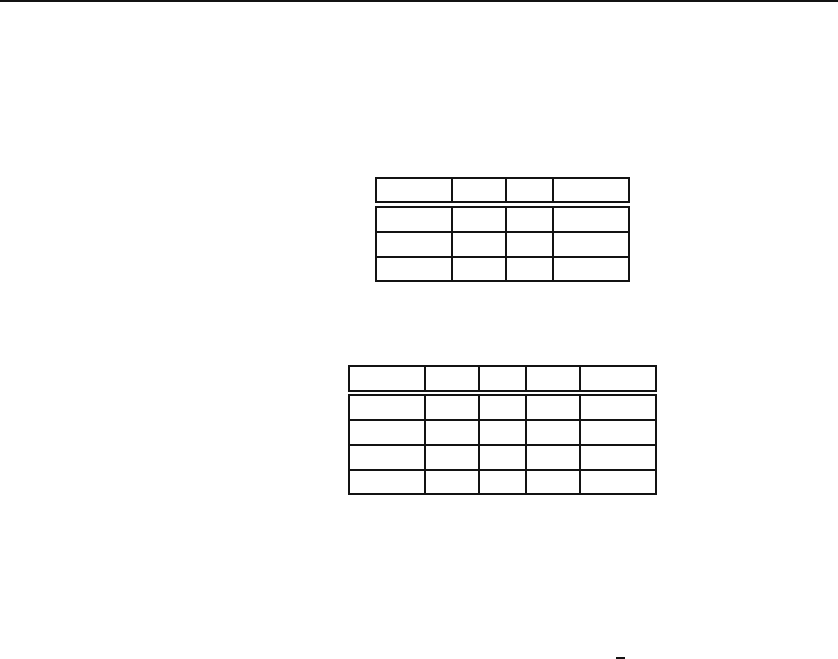
32.4. Fill in the rest of the following table assuming that all probabilities p
ij
are independent.
F
1
F
2
Total
E
1
0.3
E
2
Total 0.4
32.5. Fill in the rest of the following table assuming that all probabilities p
ij
are independent.
F
1
F
2
F
3
Total
E
1
0.3
E
2
E
3
0.5
Total 0.1 0.7
32.6. Prove Equation (32.22).
32.7. What is the probability of obtaining 400 heads in 800 coin tosses? Of
obtaining more than 500 heads? Of obtaining between 350 and 450 heads?
32.8. A graphic calculator is needed! Plot the binomial distribution
P (m, n) as a function of m for n =50andp = q =
1
2
using the exact formula
(32.27).
(a) From the plot estimate m
−
, the largest value on the left of maximum at
which the probability is (almost) zero, and m
+
, the smallest value on the right
of maximum at which the probability is (almost) zero. Compare these values
with (32.33).
(b) Sum the exact formula from m
−
to m
+
to find the probability that the
number of successes lies between m
−
and m
+
.
(c) Using the Stirling approximation (32.28) estimate the probability found
in (b) and compare the two values.
32.9. Example 32.2.2 used the exponential approximation to the binomial
distribution because the number of spins were assumed very large. Now as-
sume two systems with n
1
=8andn
2
= 12, and the total energy being
exchanged is represented by s =4.
(a) Find ˆs
1
and ˆs
2
,andshowthatˆs
1
/n
1
is (approximately) equal to ˆs
2
/n
2
and s/n.
(b) Find the ratio of the probability that s
1
=ˆs
1
−1 (and therefore, s
2
=ˆs
2
+1)
to the maximum probability. How does this compare with the same ratio
found in Example 32.2.2?

32.5 Problems 811
32.10. Using the Stirling approximation x! ≈
√
2πe
−x
x
x+1/2
of Equation
(11.6), show that
n!
m!(n −m)!
≈ 2
n
2
nπ
e
−(n−2m)
2
/2n
,
assuming that both m and n − m are large.
32.11. For the binomial distribution,
(a) show that
n
m=0
P (m, n)=
n
m=0
n
m
p
m
q
n−m
=1,
(b) and that
#
∞
−∞
P (s, n) ds =
#
∞
−∞
2
nπ
e
−s
2
/2n
ds =1.
32.12. Let r ≡
P (m,n)
P (n/2,n)
.Solveform and show that
m =
1
2
(n ±
√
n
√
−2lnr).
32.13. Show that if a/b = c/d then a/b =(a + c)/(b + d).
32.14. Derive (32.37) from (32.35).
32.15. Using the definitions of average and variance, show that σ
2
=
X
2
−X
2
.
32.16. Show directly that (32.43) satisfies
∞
n=0
p(n)=1.
32.17. A city had two earthquakes in a century. Find the probability that in
this city, there will be one earthquake
(a)nextyear,
(b) in the next 50 years.
(c) What is the probability of three or more independent earthquakes in the
same months?
32.18. The number of α particles emitted from a sample of a radioactive
atom is counted every minute for 50 hours. The total count is 1500.
(a)Whatisν for this Poisson distribution?
(b) What is the probability that in the next 6 minutes three α particles will
be emitted?
(b) What is the probability that in the next 3 minutes at least four α particles
will be emitted?
32.19. One of the first excited states of the H-atom has the wave function
Ψ(r, θ, ϕ)=Are
−r/2a
0
cos θ.

812 Probability Theory
(a) Find A so that Ψ(r, θ, ϕ) is normalized to 1.
(b) Evaluate X, Y ,andZ. Are they all zero? Do you expect them to
be?
(c) What is the expectation value of the distance of the electron from the
nucleus for this state?
32.20. Suppose that φ is a function of x
α
alone and x
α
is independent of
the rest of the variables of f (x), the density function for a multidimensional
probability space. Show that
φ(X
α
) =
##
Ω
φ(x
α
)f(x) d
m
x =
#
∞
−∞
φ(x
α
)g(x
α
) dx
α
.
32.21. The uniform probability density function over (a, b)is
f(x)=
0
1/(b −a)ifa<x<b;
0otherwise.
What is the expectation value X for this distribution?
32.22. Consider the nonnegative function
x(t)=[t(x
α
−X
α
)+(x
β
−X
β
)]
2
.
(a) Show that
x(t)=t
2
σ
2
(X
α
)+2tcov(X
α
,X
β
)+σ
2
(X
β
),
which is a parabola in the tx-plane.
(b) If the parabola is to be nonnegative, it should have at most one real root.
Show that for this to happen, the following inequality must hold:
cov
2
(X
α
,X
β
) ≤ σ
2
(X
α
)σ
2
(X
β
).
32.23. Show that
#
t
0
#
t
1
0
···
#
t
n−2
0
#
t
n−1
0
dt
n
dt
n−1
··· dt
1
=
t
n
n!
.
32.24. Let c be a positive constant and
f(x, y)=
0
cx(x + y)if0<x,0<y<1;
0otherwise.
Let u = x + y. Show that the density h(u) for the variable u is
h(u)=
0
cu
3
/2if0<u<1;
cu(u −
1
2
)ifu>1.
Show that this can be written as
h(u)=cu
.
θ(u)θ(1 − u)u
2
/2+θ(u − 1)(u −
1
2
)
/
.
