Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

772 Nonlinear Dynamics and Chaos

wings, would make it impossible to predict the long-term behavior of the

weather.

In general, for a dynamical system obeying an autonomous set of ﬁrst-

order DEs to be chaotic three requirements are to be met:

1. The trajectories must not intersect.

2. The trajectories must be bounded.

3. Nearby trajectories ought to diverge exponentially.

The ﬁrst requirement is a direct consequence of the uniqueness theorem

for

the solution of DEs: if two trajectories cross, the system will have a “choice”

for its further development starting at the intersection point, and this is not

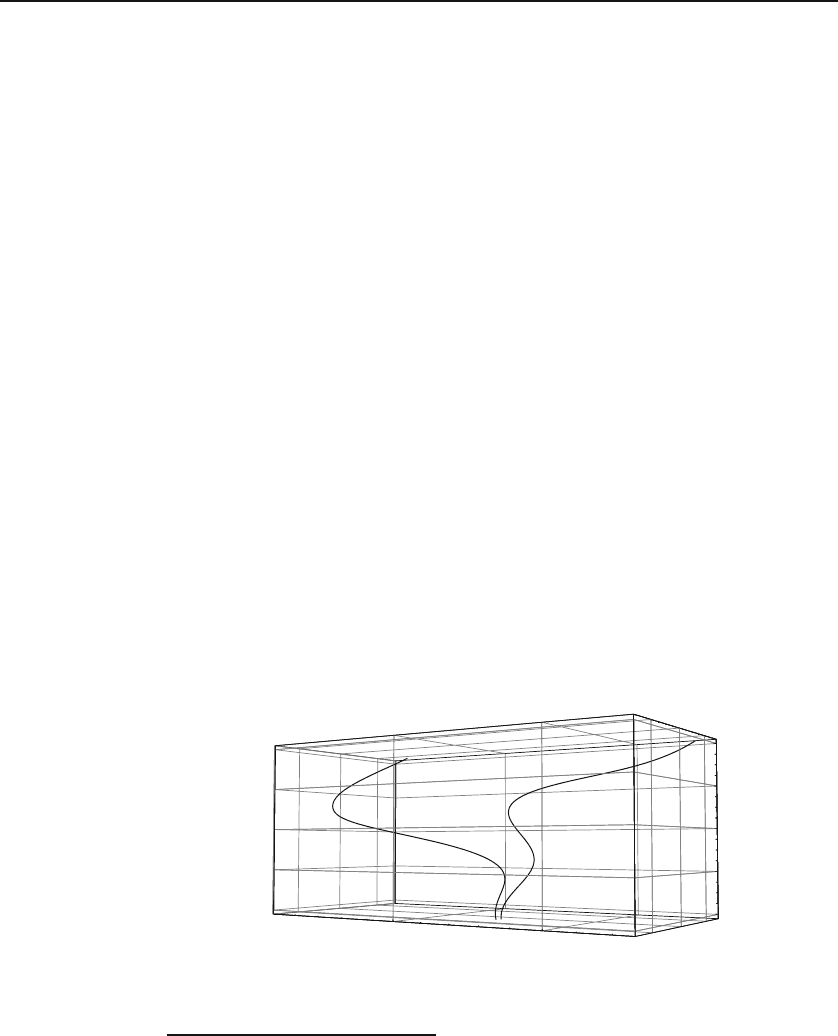
allowed. The very notion of ﬁxed point as well as the crisscrosses of Figures

31.11 and 31.12 may appear to violate the ﬁrst property above. However,

we have to remind ourselves that ﬁxed points are (asymptotically) achieved

after an inﬁnite amount of time. As for the two ﬁgures, the reader recalls

that all plots in those ﬁgures are projections of the three-dimensional trajec-

tories onto the yz-plane. The three-dimensional trajectories never cross (see

Figure 31.13).

The second requirement is important because unbounded regions of phase

space correspond to inﬁnities which are to be avoided. The third requirement

is simply what deﬁnes chaos. It turns out that one- and two-dimensional

phase spaces cannot accommodate all of these requirements. However, in

three dimensions, one can “stretch” out the trajectories that want to loop in

two dimensions as shown in Figure 31.13 where the loop of Figure 31.12 is

seen to have been only a two-dimensional shadow! Thus,

–2

–5

Figure 31.13: The two trajectories of Figure 31.12 shown in the full three-dimensional

phase space.

For our purposes this theorem states that if the dynamical variables and their ﬁrst

derivatives of a system are speciﬁed at some (initial) time, then the evolution of the system

in time is uniquely determined. In the context of phase space this means that from any

point in phase space only one trajectory can pass.

31.3 Universality of Chaos 773

Box 31.2.1. A necessary condition for a system obeying autonomous DEs

of ﬁrst degree to be chaotic is to have a phase space that has at least three

dimensions.

The reader may wonder how a (one-dimensional) pendulum can satisfy

the condition of Box 31.2.1. After all, the phase space of such a pendulum

has only two dimensions. The answer lies in the fact that although a driven

pendulum—with only θ and ω =

θ regarded as independent variables—obeys

DEs that are not autonomous, when time is turned into the third dimension

Only a driven

pendulum (of

large-angle

oscillation)

exhibits chaotic

behavior.

of the phase space, a set of three autonomous DEs will result which allows

chaotic behavior. This is in fact obvious from Equation (31.23) where α—the

third dimension of the phase space—is seen to be essentially time in units of

. A pendulum that is not driven does not exhibit chaotic behavior.

31.3 Universality of Chaos

In the preceding sections, we examined two completely diﬀerent systems dis-

playing chaotic behavior. Although there are diﬀerent “routes” to chaos, we

shall concentrate only on the period-doubling route because it has been the-

oretically developed further than the other routes, and because it displays a

universal character common to all such chaotic systems as discovered by one

of the founders of the theory of chaos, Mitchell Feigenbaum.

31.3.1 Feigenbaum Numbers

In our theoretical investigation of the logistic map, we introduced the control

parameters α

at which the nth bifurcation takes place and for which there

are a number of 2

-cycle ﬁxed points. It turns out that the ratio

≡

− α

n−1

n+1

− α

(31.24)

is almost the same for all large n, and that, in the limit as n →∞,itap-

proaches a number δ

∗

, now called the Feigenbaum delta: Feigenbaum delta

∗

≡ lim

n→∞

= lim

n→∞

− α

n−1

n+1

− α

=4.66920 .... (31.25)

Feigenbaum looked at the same ratio for the so-called iterated sine function

n+1

= β sin(πx

)

and found that exactly the same number was obtained in the limit. Later, he

showed that δ

∗

is the same for all iterated map functions!

This is not entirely true. The map functions should have a parabolic “shape” at their

maximum. The logistic map and the sine function—as well as many other functions—have

this property.

774 Nonlinear Dynamics and Chaos

We can use δ

∗

to calculate approximations to α

for large values of n, and,

in particular, to ﬁnd an approximate value for α

∞

. First we note that, if we

approximate δ

with δ

∗

, then (31.24) yields

n+1

− α

n−1

+ α

≈

− α

n−1

∗

+ α

For example,

≈

− α

∗

+ α

,α

≈

− α

∗

+ α

≈

(α

− α

)/δ

∗

+ α

=(α

− α

)



∗

∗2



+ α

We can easily generalize this to

≈ (α

− α

)



∗

∗2

+ ···+

∗(N−1)



+ α

. (31.26)

In the limit that N →∞, the sum becomes a geometric series which adds up

to 1/(δ

∗

− 1). So,

∞

≈

− α

∗

− 1

+ α

. (31.27)

With α

=3andα

=1+

√

6, we obtain

∞

≈

√

6 − 2

3.66920

+1+

√

6=3.572.

The actual value—obtained by more elaborate calculations—is 3.5699 ....

Another quantity that seems to be universal is the ratio of the consecutive

“bifurcation sizes.” We mentioned earlier that there are several ﬁxed points

associated with the 2

-cycle parameter α

. At each stage of bifurcation, these

ﬁxed points come in pairs. For example, at α

≡ 1+

√

6, Equation (31.16) gives

the two ﬁxed points at x =0.849938 and x =0.43996. We deﬁne the “size”

of the 4-cycle bifurcation as the (absolute value of the) diﬀerence between

these x-values. In general, we deﬁne d

, the size of the bifurcation pattern

of period 2

as the largest (in absolute value) of the diﬀerences between the

two x’s of each of the 2

pairs of ﬁxed points. On a bifurcation diagram, one

would measure the vertical distance between the points where each curve of the

diagram starts to branch out. If there are several such distances, one chooses

the largest one. The second Feigenbaum number, the so-called Feigenbaum

alpha, is then deﬁned as

Feigenbaum alpha

∗

≡ lim

n→∞

n+1

=2.5029 .... (31.28)

Feigenbaum found that this number is obtained for the bifurcation pattern of

all chaotic systems which reach chaos via bifurcation.

31.3 Universality of Chaos 775

Aside from its universality as applied to diﬀerent chaotic systems, this

number suggests a general “size” scaling within the bifurcation pattern of

a single system: For large enough values of n, the ratio of the size of each

bifurcation is the same as the previous one. If we “blow up” the small bifur-

cations taking place for large values of n, they look almost identical to the

ones occurring before them. This property is also called self-similarity.

self-similarity

31.3.2 Fractal Dimension

An elegant way of quantifying chaos is by examining the geometric properties

of the trajectory of the chaotic system under study. Suppose we let the system

run for a long time and suppose that it gravitates toward an attractor and

remains there.

What is the “dimension” of the trajectory? The clariﬁcation

of this question and the logic (as well as the application) of its answer is the

subject of this subsection.

Intuitively, one assigns the dimension of 0 to points, 1 to curves, 2 to

surfaces, 3 to volumes, and n to “solid” objects residing in spaces requiring

n coordinates to describe their points. How can we go beyond intuition? We

use the so-called Hausdorﬀ dimension, whose calculation goes as follows.

Hausdorﬀ

dimension

Try to cover the geometrical object by appropriate “boxes” of side length r.

Now count the number N(r) of boxes required to contain all points of the

geometric object. The Hausdorﬀ dimension D is deﬁned by

N(r) = lim

r→0

−D

, (31.29)

where k is an inessential proportionality constant which describes the shape of

the “box.” For example, as a box, we could use a “sphere” of radius r.Then

the “volume” would be 2r for a line, πr

for a circle, and

πr

for a sphere.

Thus, k is 2, or π or

π. Ifwechoose“cubes,”k will always be 1. Furthermore,

by changing the unit of length, one can change k. Fortunately, as we shall see

shortly, k will not enter the ﬁnal deﬁnition of Hausdorﬀ dimension.

Equation (31.29) can be solved for D,

D = lim

r→0



−

ln N (r)

ln r

ln k

ln r



Now, we can see why k is not essential: As r → 0 the denominator of the

second term grows beyond bound. So,

D = − lim

r→0

ln N (r)

ln r

(31.30)

Let us test (31.30) on some familiar geometric objects. If the object is a

single point on a line, then only one “box” is needed to cover it regardless of

thesizeofthebox.So,N (r) = 1 for all r, and Equation (31.30) gives D =0.

By an attractor, we mean any geometrical object on which the trajectory hovers. It can

be a ﬁxed point, a limit cycle, or some multidimensional object in the phase (hyper-)space.

776 Nonlinear Dynamics and Chaos

In fact, the Hausdorﬀ dimension of any ﬁnite number of points on a line is

found to be zero. Similarly, the dimension of a ﬁnite number of points on a

surface or in a volume is also zero.

If the object is a surface of area A, then we require A/r

boxes (squares)

to cover the entire area. Thus,

D = − lim

r→0

ln(A/r

)

ln r

= − lim

r→0



ln A −2lnr

ln r



=2.

Similarly, the reader may check that the Hausdorﬀ dimension for a curve is

1, and for a volume it is 3. So, the formula seems to be working for familiar

geometric objects.

Example 31.3.1.

A not-so-familiar geometric object is the Cantor set:TaketheCantor set

closed interval [0, 1]; remove its middle third; do the same with the remaining two

segments; continue the process ad inﬁnitum (Figure 31.14). What is left of the line

segment is the Cantor set, named after the German mathematician whose work on

set theory, controversial at the time, laid the foundation of modern formal mathe-

matics. Figure 31.14 should convince the reader that after n steps, 2

segments are

left and that the length of each segment is (1/3)

. Thus, denoting the size of the

box after n steps by r

,wehave

=(1/3)

,N(r

)=2

Therefore,

D = − lim

r→0

ln N(r)

ln r

= − lim

n→∞

ln N(r

)

ln r

= − lim

n→∞

ln(2

)

ln[(1/3)

]

= − lim

n→∞

n ln 2

n ln(1/3)

= −

ln 2

ln(1/3)

ln 2

ln 3

=0.6309 .... (31.31)

So, the Cantor set is more than just a set of points (dimension zero) and less than a

line segment (dimension one). It is amusing to note—as the reader may verify—that

the length of the Cantor set is zero!



The Cantor set is only one example of geometrical objects whose dimen-

sions are nonintegers:

fractal object or

fractal

Figure 31.14: The Cantor set after one, two, three, and four “dissections.”

31.3 Universality of Chaos 777

Box 31.3.1. A geometrical object, whose Hausdorﬀ dimension in not an

integer, is called a fractal object or simply a fractal.

Example 31.3.2. Another example of a fractal object is the so-called Koch

snowﬂake. Start with an equilateral triangle of side L [Figure 31.15(a)]; remove Koch snowﬂake

the middle third of each side and replace it with two identical segments (a “wedge”)

to form a star [Figure 31.15(b)]. Do the same to the small segments so obtained

[Figure 31.15(c)], and continue ad inﬁnitum. The result is the Koch snowﬂake.

Let us ﬁnd the Hausdorﬀ dimension of the Koch snowﬂake.

It should be clear Aﬁnitearea

bounded by an

inﬁnite closed

curve!

that the number of line segments on each side of the triangle at step n is 4

so that

N(r

)=3× 4

,andthelengthr

of each line segment is L/3

. Therefore, the

Hausdorﬀ dimension of the Koch snowﬂake is

D = − lim

n→∞

ln N(r

)

ln r

= − lim

n→∞

ln(3 × 4

)

ln(L/3

)

= − lim

n→∞

ln 3 + n ln 4

ln L − n ln 3

ln 4

ln 3

=1.2618595 .... (31.32)

The length of the perimeter of the snowﬂake is

lim

n→∞

N(r

= lim

n→∞

(3 × 4

)(L/3

)=3L lim

n→∞

→∞.

It is interesting to note that the area enclosed by the Koch snowﬂake is ﬁnite while

its perimeter is inﬁnite!



The fractals discussed so far have the property which we called self-similarity.

The present case is, however, a true (or regular) self-similarity because, as we

scale the object, we obtain the exact replica of the original. In contrast, for

(a) (b) (c)

Figure 31.15: (a) Begin with an equilateral triangle. (b) Remove the middle third of

each side and replace it with a “wedge” to form a star. (c) Remove the middle third of

each new segment and replace them with “wedges.” Continue ad inﬁnitum to obtain

the Koch snowﬂake.

This is the dimension of the perimeter, not the area of the snowﬂake.

778 Nonlinear Dynamics and Chaos

the logistic map, we obtained bifurcations which contained diﬀerent scaling

ratios: The ratio was α

∗

only for the largest bifurcation size at each stage.

Comparison of the largest size with smaller sizes would not have yielded α

∗

These (irregular) self-similarities occur frequently in chaotic systems and the

determination of their Hausdorﬀ dimension can give information about the

long-term behavior of the dynamics of the system.

In the case of the logistic map, the Hausdorﬀ dimension of the set of verti-

cal (ﬁxed) points on the bifurcation diagram—which is zero at all ﬁnite stages

of bifurcation—will not be zero at α

∞

. It has, in fact, been calculated to be

0.5388 .... This is an example of attractors that have noninteger dimensions,

i.e., they are neither points nor lines. If the attractor of a dissipative dy-

namical system has a fractal dimension, then we say that the system has a

strange attractor

strange attractor. Strange attractors play a fundamental role in the theory

of chaos.

31.4 Problems

31.1. Show that (31.1) leads to (31.2).

31.2. For the logistic map, assume that 1 <α<3. Show that if x

> 1−1/α,

then x

k+1

,andifx

< 1 − 1/α,thenx

k+1

. Therefore, conclude

that x

∗

=1− 1/α is a stable ﬁxed point.

31.3. Write the cubic polynomial in Equation (31.10) as



x − 1+



+ ax + b)

and determine a and b by expanding and comparing the result with (31.10).

Now solve x

+ ax + b = 0 to obtain x

(α)andx

(α) of (31.11).

31.4. Derive Equation (31.21) from the equation that precedes it.

31.5. Convince yourself that a system of N particles in space has a 6N-

dimensional phase space.

31.6. Consider a set of autonomous ﬁrst-order DEs. Suppose that a point P

of the phase space is a root of all functions on the RHS. By expanding each

coordinate of a trajectory in a Maclaurin series in t and keeping only the ﬁrst

two terms, show that the trajectory does not move away from P .So,ﬁxed

points are determined by setting all functions on the RHS of an autonomous

system equal to zero and solving for the coordinates.

31.7. Derive Equation (31.27) from (31.26).

31.8. Show that the dimension of a ﬁnite number of points on a surface or

in a volume is zero.

31.4 Problems 779

31.9. Show that the Hausdorﬀ dimension of any ﬁnite number of points is

zero, of a curve is 1, and of a volume is 3.

31.10. Show that the Hausdorﬀ dimension of the Cantor set is independent

of the length of the original line segment.

31.11. Verify that the length of the Cantor set is zero.

Chapter 32

Probability Theory

Although probability theory did not ﬂourish until after the Renaissance, and

in particular in the 17th and 18th centuries, its roots go back to ancient

history. Archaeological excavations reveal the presence of knuckle-bones (or

astragali) in numbers far larger than any other kind of bones, indicating the

possibility of the use of these bones in games. There is strong evidence that as-

tragali were in use for board games at the time of The First Dynasty in Egypt

(c.3500 B.C.). Other archaeological excavations, unearthing more recent pe-

riods, e.g. 1300 B.C. in Turkey, also reveal a deﬁnite connection between

astragalus and recreation.

It seems that games of chance, such as the board game mentioned above,

are, like counting, as old as civilization itself. Yet the science of counting,

arithmetic, was already in an advanced stage of evolution when probability

started to take root as a mathematical science in the 17th century. Why?

Perhaps the reason is the crudeness with which “randomizers” such as dice—

the artiﬁcial substitutes of astragali—were made for a long time. Abstraction

requires perfection. Although the abstraction of counting from what was being

counted took place naturally, the corresponding abstraction of randomness

from what is random demanded an ideal device capable of producing random

events, and a large number of experimental data for analysis, and this did not

happen until well into the 17th century.

32.1 Basic Concepts

The reader no doubt has some familiarity with the notion of a random event. Random event:

basis for

probability

Any occurrence or experiment, whose outcome is uncertain is such an event.

Flipping a coin, pulling a card out of a deck of cards, and throwing a die

are all examples of experiments whose outcome are uncertain (if the coin, the

deck of cards, and the die are all “unbiased”). The reader may also know

intuitively that the chance of getting a head in the toss of a coin is 50% (or

1 out of 2, or 0.5); that the chance of getting a 3 in the throw of a die is 1

782 Probability Theory

out of 6; and that the chance of getting a club in drawing a card is 1 out of 4.

The aim of the theory of probability is to make precise these intuitive notions

and to develop a mathematical procedure for answering questions related to

random events. First we need to review some simple concepts from set theory.

32.1.1 A Set Theory Primer

The most fundamental entity in any branch of mathematics is a universal

set. It is the collection of all objects under consideration. For example, the

Universal set

universal set of plane geometry is a ﬂat surface, and of solid geometry is

the three-dimensional space. The universal set of calculus is the set of real

numbers (or the real line), and the complex plane is the universal set of

complex analysis. The generic universal set is denoted by S, but each speciﬁc

universal set has its own symbol: R is the set of real numbers, C is the set of

complex numbers, Z is the set of integers, and N is the set of natural numbers

(nonnegative integers).

The simplest relation in set theory is that of belonging. We write a ∈ S

(and say “a belongs to S”or“a is in S”toexpressthefactthata is one of

the objects in S. An object in S is called an element of S. A collection A

Element and

subset of a set

of elements of S is called a subset of S,andwewriteA ⊂ S.Inparticular,

S ⊂ S. Any subset can be considered as a set with its elements and subsets.

Thus, a ∈ A means that a is one of the elements of the subset A, a ∈ A

means that a is not one of the elements A,andB ⊂ A means that B consists

of elements, all of which belong to A. Subsets are often speciﬁed either by

enumeration or by some statement enclosed between a pair of curly brackets.

For example,

{0, 1, 2, 3,...}, {2, 4, 6,...}, {2n +1|n ∈ N},

{(x, x)|x ∈ R},

(

−

13.6



n ∈ N,n =0

)

The ﬁrst describes N; the second, the set of even numbers; the third, the set of

odd numbers; the fourth, the line y = x; and the ﬁfth, the energy levels of the

hydrogen atom in electron volt. Two subsets are equal if each is a subset of

the other. In other words, if A ⊂ B and B ⊂ A,thenA = B.Itisconvenient

to introduce the empty set, a subset ∅ of S, which has no element.

The subsets of a universal set have a rich mathematics which we can only

brieﬂy outline here. Given two sets

A and B, we can form another set, called

the union of A and B and denoted by A ∪ B, which consists of all elements

belonging to either A or B or both. Thus,

A ∪B = {x ∈ S|x ∈ A or x ∈ B}.

It is very common to delete the preﬁx ‘sub’ and refer to subsets of a universal set as

simply sets.