Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

30.4 Problems 751

30.9. Among all curves joining a given point (0,b)onthey-axistoapoint

on the x-axis and enclosing a given area S together with the x-axis, ﬁnd the

curve which generates the least area when rotated about the x-axis.

30.10. An Atwood machine consists of two masses m

and m

connected by

a light inextensible cord of length l which passes over a pulley whose radius

is a and whose moment of inertia is I.Letx denote the distance of m

from

the top of the pulley. Using Lagrangian methos, show that the acceleration

of m

¨x =

g(m

− m

)

+ m

+ I/a

30.11. Using polar coordinates, write the Lagrangian of a particle of mass m

moving in a central force ﬁeld with potential Φ(r). Show that the equations

of motion are

m¨r = mr

−

dΦ

(mr

θ)=0.

30.12. Using Lagrangian method, ﬁnd the acceleration of a solid sphere

rolling without sliding down an inclined plane having an angle θ with the

horizontal.

30.13. Using Lagrangian method, ﬁnd the acceleration of a solid sphere

rolling without sliding down a movable wedge of mass M having an angle

θ. The wedge moves on a frictionless horzontal surface.

30.14. Two blocks of equal mass m are connected by an inextensible cord

whose linear mass density is μ. One block is placed on a smooth horizontal

table, the other hangs over the edge of the table. What is the acceleration of

the system? Use the Lagrangian method.

30.15. A simple pendulum of length l and mass m oscillates about its point of

support which is attached to a block of mass M moving without friction along

a horizontal line lying in the plane of the pendulum. Write the Lagrangian in

terms of x, the position of M on the horizontal line, and θ, the angle l makes

with the vertical. Find the equations of motion of m and M .

30.16. Find the equation of a curve describing the equilibrium position of

a uniformly dense heavy ﬂexible inextensible cord of length l fastened at its

ends. Hint: The Lagrangian is just the potential energy written as an integral.

30.17. Show that the Lagrangian density (30.43) can be written as

L =



|B|

−|E|



+ μ

(ρΦ −J · A) .

Hint: See Sections 17.3.1 and 17.3.2 and be careful about possible change of

sign when raising or lowering indices.

30.18. Show that the Lagrangian density (30.47) leads to the Klein-Gordon

equation.

Chapter 31

Nonlinear Dynamics

and Chaos

A variety of techniques including the Frobenius method of inﬁnite power series

could solve almost all linear DEs of physical interest. However, some very fun-

damental questions such as the stability of the solar system led to DEs that

were not linear, and for such DEs no analytic (including series representation)

solution existed. In the 1890s, Henri Poincar´e, the great French mathemati-

cian, took upon himself the task of gleaning as much information from the

DEs describing the whole solar system as was possible. The result was the

invention of one of the most powerful branches of mathematics (topology) and

the realization that the qualitative analysis of (nonlinear) DEs could be very

useful.

One of the discoveries made by Poincar´e, which much later became the

cornerstone of many developments, was that

Box 31.0.1. Unlike the linear DEs, nonlinear DEs may be very sensitive

to the initial conditions.

In other words, if a nonlinear system starts from some initial conditions and

develops into a certain ﬁnal conﬁguration, then starting it with slightly dif-

ferent initial conditions may cause the system to develop into a ﬁnal conﬁg-

uration completely diﬀerent from the ﬁrst one. This is in complete contrast

to the linear DEs where two nearby initial conditions lead to nearby ﬁnal

conﬁgurations.

In general, the initial conditions are not known with inﬁnite accuracy.

Therefore, the ﬁnal states of a nonlinear dynamical system may exhibit an

indeterministic behavior resulting from the initial (small) uncertainties. This

is what has come to be known as chaos. The reader should note that the inde-

chaos due to

uncertainty in

initial conditions

terminism discussed here has nothing to do with the quantum indeterminism.

754 Nonlinear Dynamics and Chaos

All equations here are completely deterministic. It is the divergence of the

initially nearby—and completely deterministic—trajectories that results in

unpredictable ﬁnal states.

There are two general categories exhibiting chaotic behavior: systems

obeying iterated maps and systems obeying DEs. We shall study the ﬁrst

category in some detail, and only outline some of the general features of the

much more complicated category of systems obeying DEs.

31.1 Systems Obeying Iterated Maps

Consider the population of a species in consecutive years if the population is

initially N

. The simplest relation connecting N

, the population after one

year, to N

= αN

where α is a positive number depending on the environment in which the

species lives. Under the most favorable conditions, α is a large number, indi-

cating rapid growth of population. Under less favorable conditions, α will be

small. And if the environment happens to be hostile, then α will be smaller

than one, indicating a decline in population.

The above equation is unrealistic because we know that if α>1andthe

population grows excessively, there will not be enough food to support the

species. So, there must be a mechanism to suppress the growth. A more

realistic equation should have a suppressive term which is small for small N

and grows for larger values of N

. A possible term having such properties is

one proportional to N

. This leads to

= αN

− βN

where 0 <β α.

The minus sign causes the second term to decrease the population. Iterating

this equation, we can ﬁnd the population in the second, third, and subsequent

years:

= αN

− βN

= αN

− βN

,...,

and, in general,

k+1

= αN

− βN

. (31.1)

It is customary to rewrite (31.1) in a slightly diﬀerent form. First we note

that since population cannot be negative, there exists a maximum number

beyond which the population cannot grow. In order for N

k+1

to be positive,

we must have

αN

− βN

> 0 ⇒ N

for all k. It follows that N

max

= α/β. Dividing (31.1) by N

max

yields

k+1

= αx

(1 −x

), (31.2)

31.1 Systems Obeying Iterated Maps 755

where x

is the fraction of the maximum population of the species after k

years, and therefore, its value must lie between zero and one. Any equation

of the form

k+1

= f

), (31.3)

where α is—as in the case of the logistic map—a control parameter, and in

which a value of some (discrete) quantity at k + 1 is given in terms of its value

at k, is called an iterated map, and the function f

is called the iterated iterated map,

iterated map

function, and

logistic map

function

map function. The particular function in (31.2) is called the logistic map

function.

Starting from an initial value x

, one can generate a sequence of x values

by consecutively substituting in the RHS of (31.3). This sequence is called a

trajectory or orbit of the iterated map.

31.1.1 Stable and Unstable Fixed Points

It is clear that the ﬁrst few points of an orbit depend on the starting point.

What may not be so clear is that, for a given α, the eventual behavior of

the orbit is fairly insensitive to the starting point. There are, however, some

starting points which are manifestly diﬀerent from others. For example, in the

logistic map, if x

= 0, no other point will be produced by iteration because

(0) = 0 or f

)=x

, and further application of f

will not produce any

new values of x. In general, a point x

which has the property that

)=x

(31.4)

is called a ﬁxed point of the iterated map associated with α. For the logistic

ﬁxed point of an

iterated map

map we have

= αx

(1 −x

) ⇒ x

(1 −α + αx

)=0 ⇒ x

=0, 1 −

. (31.5)

Since 0 ≤ x

≤ 1, there is only one ﬁxed point (i.e., x =0)forα ≤ 1, and

two ﬁxed points (i.e., x =0andx =1−1/α)forα>1.

What is the signiﬁcance of ﬁxed points? When α<1, Equation (31.2)

shows—since both x

and 1 −x

are at most one—that the population keeps

decreasing until it vanishes completely. And this is independent of the initial

graphical way of

approaching a

ﬁxed point

value of x. It is instructive to show this pictorially. Figure 31.1(a) shows the

logistic map function with α =0.5. Start at any point x

on the horizontal

axis; draw a vertical line to intersect the logistic map function at f(x

) ≡ x

;

from the intersection draw a horizontal line to intersect the line y = x at y

; draw a vertical line to intersect the logistic map function at f (x

) ≡ x

;

continue to ﬁnd x

and the rest of x’s. The diagram shows that the x’s are

getting smaller and smaller.

What happens when α>1? Figure 31.1(b) shows the logistic map function

with α = 2. We note that the orbit is attracted to the ﬁxed point at x =

0.5. We also note that the ﬁxed point at x = 0 has now turned into a

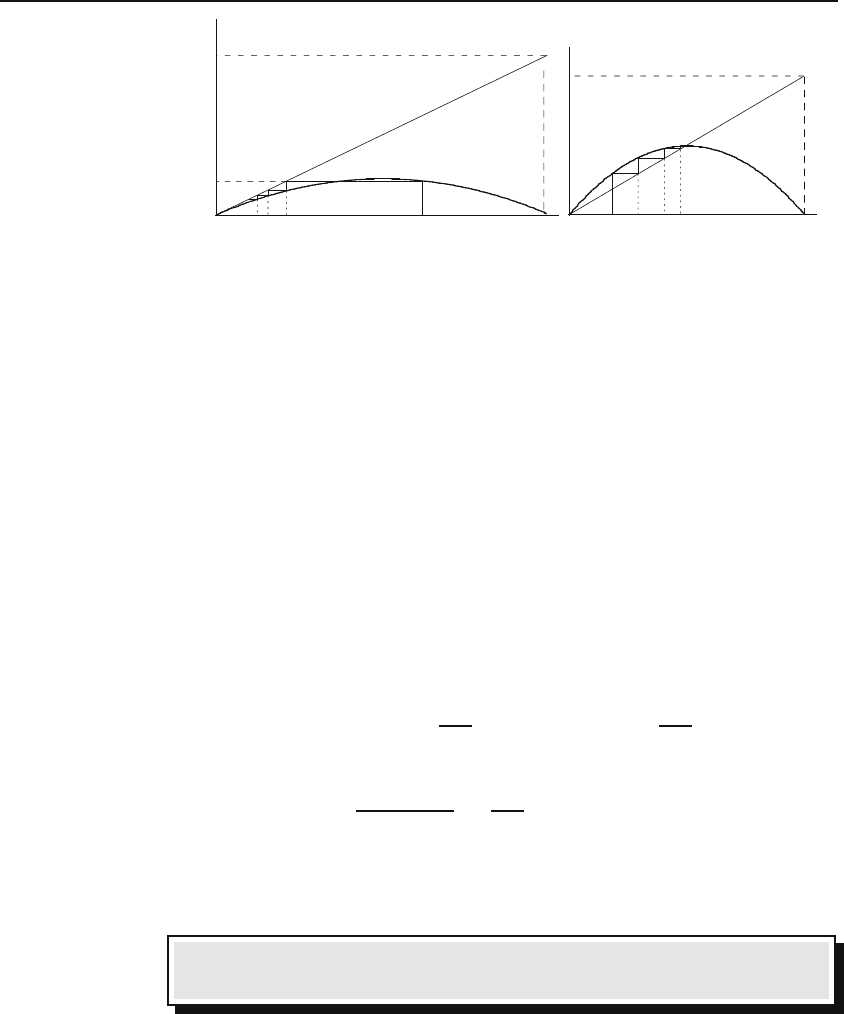
756 Nonlinear Dynamics and Chaos

= 2

y = f

(

)

y = x

= 0.5

y = f

(

)

y = x

f (x

)

(a) (b)

Figure 31.1: (a) Regardless of the value of x

, the orbit always ends up at the origin

when α<1.(b)Evenforα>1, it appears that the orbit always ends up at some

attractor regardless of the value of x

. Note that now the origin has become a “repellor.”

“repellor.” We can treat the behavior of the logistic map at general ﬁxed

points analytically.

First let us consider a general (one-dimensional) iterated map as given by

Equation (31.3). We are seeking the ﬁxed points of (31.3). These points—

commonly labeled by an asterisk—satisfy

∗

= f

∗

i.e., they are intersections of the curves y = x and y = f

(x)inthexy-plane.

An important property of ﬁxed points is their stability—or whether they are

attractors or repellors. To test this property, we Taylor-expand the iterated

stability of ﬁxed

points

map function around x

∗

, keeping the ﬁrst two terms:

k+1

= f

)=f

∗



∗

− x

∗

)=x

∗



∗

− x

∗

)

k+1

− x

∗

− x

∗



∗

= |f



∗

)|.

So, x

k+1

will be farther away from (or closer to) x

∗

than x

if the absolute

value of the derivative of the function is greater than one (or less than one).

analytic criterion

for stability of a

ﬁxed point of an

iterated map

Box 31.1.1. Aﬁxedpointx

∗

of an iterated map (31.3) is stable if



∗

)| < 1 and unstable if |f



∗

)| > 1.

Example 31.1.1. For the logistic map, f

(x)=αx(1−x)sothatf



(x)=α−2αx.

The ﬁxed points are x

∗

=0andx

∗

=1−1/α. Therefore,



∗

)=f



(0) = α and f



∗

)=f



(1 − 1/α)=2− α. (31.6)

31.1 Systems Obeying Iterated Maps 757

It follows that the ﬁxed point at x = 0 is stable (attractive) if α<1, while for

this same value of α the ﬁxed point x

∗

is unstable (repulsive). Thus, for α<1, all

trajectories are attracted to the ﬁxed point at x =0.

Equation (31.6) also shows that for 1 <α<3, the other ﬁxed point becomes

stable while the ﬁxed point at the origin becomes unstable. This is also consistent

with the behavior of the logistic map depicted in Figure 31.1(b).



The criterion of Box 31.1.1 can also be stated graphically. Since 1 is the

slope of the line y = x, and since a ﬁxed point is an intersection of the two

curves y = x and y = f

(x), the criterion of Box 31.1.1 is a comparison of the

slope of the tangent to y = f

(x)withtheslopeofy = x:Aﬁxedpointx

∗

of an iterated map (31.3) is stable, if the acute angle that the tangent line at

∗

)) makes with the x-axis is smaller than the corresponding angle of

the line y = x. If this angle is larger, then the ﬁxed point is unstable. This is

equivalent to the simpler statement:

graphical criterion

for stability of a

ﬁxed point of an

iterated map

Box 31.1.2. Aﬁxedpointx

∗

of an iterated map f

(x) is stable (unstable)

if immediately to the right of x

∗

,thecurvey = f

(x) lies below (above)

the line y = x.

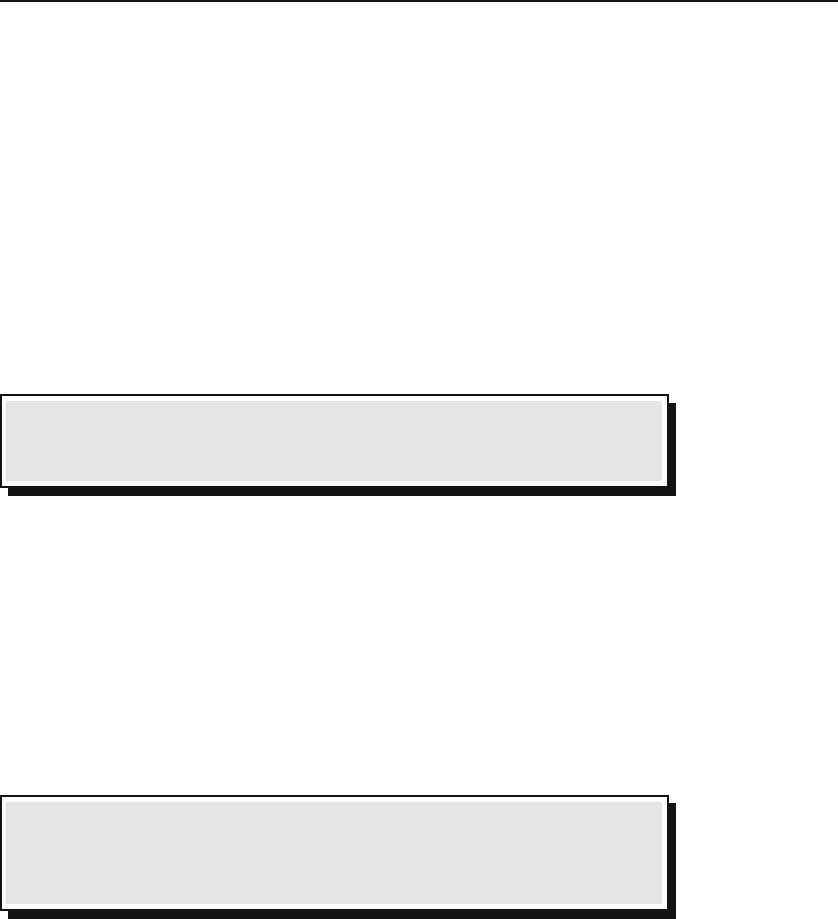
31.1.2 Bifurcation

Although the logistic map has no stable ﬁxed points beyond x

=1−1/α,we

may ask whether there are points at which the iterated map is “semi-stable.”

What does this mean? Instead of demanding strict stability or instability, let

us consider a case in which the map may oscillate between two values.This

situation is neither completely stable nor completely unstable: Although the

system moves away from the point in question, it does not leave it forever.

Suppose that just above the largest value of a stable α, the system starts to

oscillate between two values of x. This is an example of bifurcation:

bifurcation and

period doubling

Box 31.1.3. When the development of a system splits into two regions as

a parameter of the equations of motion of the system increases slightly, we

say that a bifurcation has occurred and call the splitting of the trajectory

a period-doubling bifurcation.

Suppose that there are two “ﬁxed” points x

∗

and x

∗

between which the

function oscillates such as the two points illustrated in Figure 31.2(a). These

ﬁxed points must satisfy

∗

= f

∗

),x

∗

= f

∗

). (31.7)

To gain further insight into the behavior of the logistic map, we introduce the

so-called second iterate of f

denoted by f

[2]

and deﬁned by second iterate

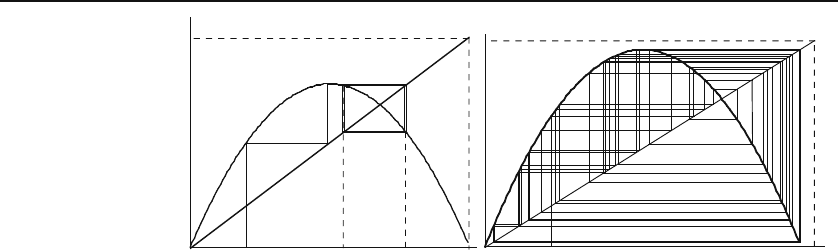
758 Nonlinear Dynamics and Chaos

0.2

0.558

0.7646

(a)

(b)

Figure 31.2: (a) For α =3.1, there are clearly two attractors located at x =0.5580

and x =0.7646.(b)Forα =3.99, no attractor seems to exist because the iterations

do not seem to converge in the diagram.

[2]

(x) ≡ f

(x)). (31.8)

From this deﬁnition, it is clear that every ﬁxed point of f

is also a ﬁxed

point of f

[2]

. However, the converse statement is not true. In fact, x

∗

and x

∗

deﬁned in Equation (31.7) are ﬁxed points of f

[2]

∗

)=f

∗

)) = f

∗

)=x

∗

[2]

∗

)=f

∗

)) = f

∗

)=x

∗

but not of f

. It now follows that ﬁxed points of f

[2]

give information about

period-doubling bifurcation.

For the logistic map, f

[2]

can be found easily:

[2]

(x)=f

(x)) = αf

(x)[1 −f

(x)]

= α[αx(1 −x)][1 −αx(1 − x)] = α

x(1 − x)(1 −αx + αx

)

= −α

+2α

− (α

+ α

x. (31.9)

The ﬁxed points of f

[2]

(x) are, therefore, determined by the equation

x = −α

+2α

− (α

+ α

which shows that there are, in general, four ﬁxed points, one at x =0,and

three others satisfying the cubic equation

− 2α

+(α

+ α

)x −α

+1=0. (31.10)

We can actually solve this equation because we know that one of its roots is

(α)=1− 1/α,aﬁxedpointoff

(x). The cubic polynomial in Equation

31.1 Systems Obeying Iterated Maps 759

(31.10) can thus be factored out as α

[x−x

(α)] times a quadratic polynomial

whose roots give the remaining solutions to (31.10). The reader may verify

that these roots are

(α)=

1+α +

√

− 2α − 3

2α

(α)=

1+α −

√

− 2α − 3

2α

. (31.11)

These two functions start out at the common value of

when α = 3. Then, as

a function of α, x

(α) monotonically increases and asymptotically approaches

1; x

(α) monotonically decreases and asymptotically approaches 0.

We are interested in those values of α for which the ﬁxed points are not

completely unstable. In the present case, this means that the value of the

iterated map must oscillate between only two values. This will happen only

if the two points are stable ﬁxed points of f

[2]

. Since by Box 31.1.1 stability

imposes a condition on the derivative of the function, we need to look at the

derivative of f

[2]

Using the chain rule, which in its most general form is

[g(h(x))] = g



(h(x))h



(x)

we obtain

[2]

(x)=[f



(x))]f



(x). (31.12)

In particular, if x happens to be a ﬁxed point x

∗

of f

,then

[2]



∗

= f



∗

)



 

∗



∗

)=[f



∗

)]

. (31.13)

This shows that if x

∗

is a stable ﬁxed point of f

,then



∗

)| < 1 ⇒ [f



∗

)]

< 1 ⇒



[2]

∗

)



< 1

and x

∗

is a stable ﬁxed point of f

[2]

as well. Furthermore, at the two ﬁxed

points of f

[2]

discussed above, Equation (31.12) yields

[2]



∗

= f



∗

)



 

∗



∗

)=f



∗



∗

[2]



∗

= f



∗

)



 

∗



∗

)=f



∗



∗

). (31.14)

It follows that f

[2]

has the same derivatives at these two points.

760 Nonlinear Dynamics and Chaos

The concept of iteration of f

can be readily generalized. The nth iteratenth iterate

of f

[n]

≡ f (f (...f



 

n times

(x) ...))

and as in the case of f

[2]

, the ﬁxed points of f

are also ﬁxed points of f

[n]

and

the stable ﬁxed points of f

are also stable ﬁxed points of f

[n]

. The converse

of neither of these statements is, in general, true.

The utility of the concept of the nth iterate comes in the analysis of the

location of bifurcation points. To be speciﬁc, let us go back to the logistic map

and Equation (31.6). The stable points, being characterized by the absolute

value of the derivative of the map function, occur at x =0when0<α<1

and at x =1− 1/α when 1 <α<3. Within the α-range of stability, the

derivative of f

ranges between

−1and+1,startingwith+1atα =1and

ending with −1atα = 3 [see the second equation in (31.6)]. Beyond this

value of α—which is the parameter at which the 2-cycle ﬁxed point occurs

and which we now denote by α

—f

has no stable points. Equation (31.13),

however, shows that the derivative of f

[2]

is +1 there. This means that the

derivative of f

[2]

can decrease down to −1asα increases beyond α

.Infact,

what happens as α increases past α

is precisely a repetition of what happened

to f

between α =1andα = 3: The derivative of f

[2]

keeps decreasing until

at a certain value of α denoted by α

a period-doubling bifurcation occurs

for f

[2]

. This corresponds to a 4-cycle ﬁxed point. Thus a 4-cycle ﬁxed point4-cycle ﬁxed point

∗

, as well as the corresponding value of α, is obtained by imposing the two

requirements

[2]

∗

)=x

∗

and

[2]



∗

= −1. (31.15)

This equation entails an important result. By Equation (31.14), the derivative

of f

[2]

at its two stable points are equal. Therefore, both stable points give

rise to the same pair of equations (31.15). In particular,

Box 31.1.4. Any value of α

that gives a solution for the ﬁrst ﬁxed point

must also give a solution for the second ﬁxed point. In fact, we should ex-

pect two values of x

∗

for every α

that solves the pair of equations (31.15).

For the logistic map, Equation (31.15) becomes [see (31.9)]

∗

= α

∗

(1 −x

∗

)(1 −α

∗

+ α

∗2

−1=−4α

∗3

+6α

∗2

− 2(α

+ α

∗

+ α

The x = 0 is an exception because we are assuming that α is a positive quantity,

therefore, f



(0) = α cannot be negative.

31.1 Systems Obeying Iterated Maps 761

One can solve these equations and obtain eight possible pairs (x

∗

,α

). The

only two acceptable real pairs which have a value of α

larger than three are



√

6 ±



14 − 4

√

, 1+

√



=(0.644949 ± 0.204989, 3.44949). (31.16)

In particular, α

=1+

√

6=3.44949 is the 4-cycle ﬁxed point depicted in

Figure 31.3 corresponding to the two x values of approximately 0.85 and 0.44.

The generalization to 2

-cycles is now clear. One simply constructs the

th iterate of f

and solves the two equations

]

∗

)=x

∗

and

]



∗

= −1.

In practice, these are too complicated to solve analytically, but numerical

methods are available for their solution. Each solution consists of a pair

∗

,α

)wherex

∗

is the 2

-cycle ﬁxed point and α

is the corresponding

control parameter. As in the case of f

[2]

, for each acceptable α

,thereare2

ﬁxed points.

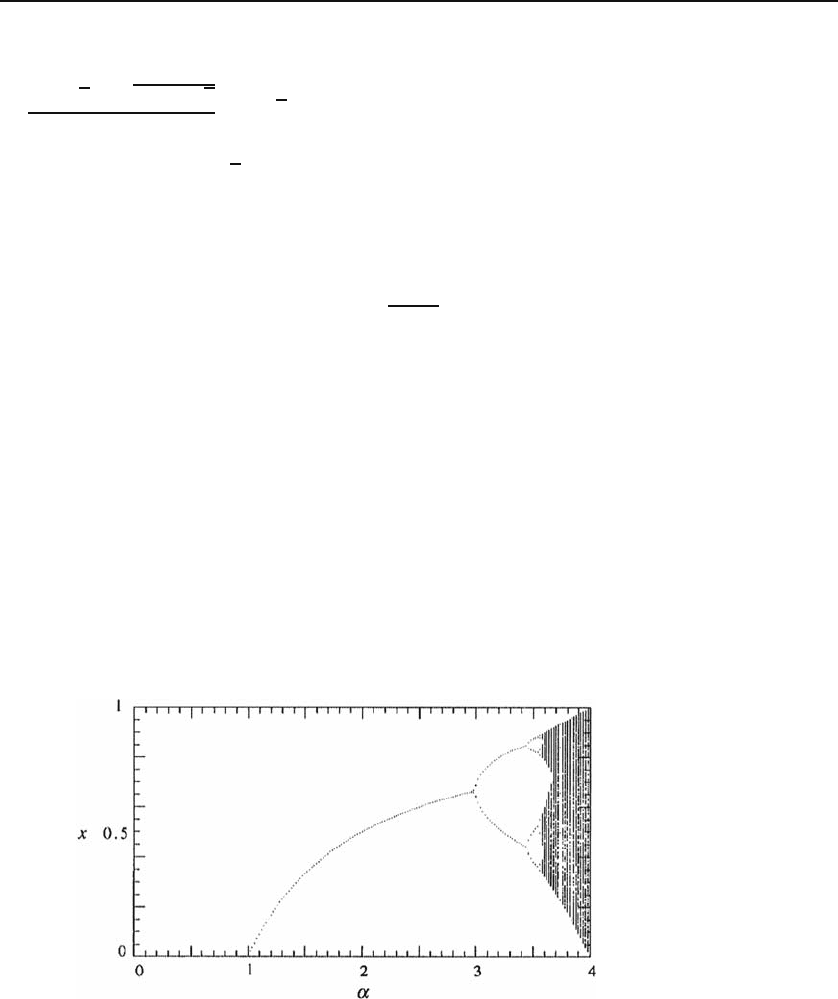
31.1.3 Onset of Chaos

Suppose we keep increasing α slowly. It may happen that at a certain value of

α no ﬁnite set of “stable” points exists. A graphical analysis of this situation

is depicted in Figure 31.2(b) showing that the behavior of the logistic map

is chaotic. What is the relation between the value of α at which chaos sets

in (which we denote by α

)andα

? Considering the chaotic behavior as

Figure 31.3: The bifurcation diagram for the logistic map. The behavior of the function

is analytically very simple for α<3.Forα>3, the behavior is more complicated. The

4-cycle ﬁxed points are clearly shown to occur at α ≈ 3.45. From approximately 3.57

onward, chaotic behavior sets in.