Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

32.1 Basic Concepts 783

The intersection of A and B, denoted by A ∩B, consists of all elements that Union,

intersection, and

complement

belong to both A and B:

A ∩B = {x ∈ S|x ∈ A and x ∈ B}.

The complement of a set A is the subset of S which contains all the elements

of S which are not in A. Denoting this set by A

,wehave

= {x ∈ S|x ∈ A}.

The reader may easily verify that S = A∪A

and ∅ = A∩A

.WhenA∩B = ∅,

we say that A and B are disjoint.

Disjoint sets

The operations of union and intersection are commutative and associative:

A ∪ B = B ∪ A, A ∩B = B ∩ A,

(A ∪ B) ∪ C = A ∪(B ∪ C), (A ∩B) ∩ C = A ∩ (B ∩ C).

Thus one can take the union and intersection of a number of sets without wor-

rying about the order of the sets or where to put the parentheses. This makes

it possible to introduce the following notations for the union and intersection

of a family of sets:

i=1

≡ A

∪ A

∪···∪A

i=1

≡ A

∩ A

∩···∩A

. (32.1)

We deﬁne the diﬀerence between two sets A −B ≡ A∩B

as the collection

of elements in A that are not in B. It is not hard to show that A −B, B −A,

and A ∩ B are mutually disjoint. Furthermore,

A =(A −B) ∪ (A ∩ B),

B =(B −A) ∪ (A ∩ B), (32.2)

A ∪B =(A −B) ∪ (A ∩ B) ∪ (B − A).

Note that all sets on the right-hand side of each equation are mutually disjoint.

A useful way of picturing sets and operations on them is a Venn diagram.

Venn diagrams

The universal set is depicted as a rectangle, and its subsets as circles in the

rectangle. Figure 32.1 shows some examples of the use of Venn diagrams.

Venn diagrams are intuitive representations of relations among sets. For ex-

ample, the diagram on the right of Figure 32.1 shows clearly the equalities of

Equation (32.2).

Using Venn diagrams, one can show that the operation of union distributes

over intersection and vice versa:

A ∩ (B ∪ C)=(A ∩ B) ∪ (A ∩ C),

A ∪ (B ∩ C)=(A ∪ B) ∩ (A ∪ C), (32.3)

784 Probability Theory

A ∩ B

A ∪ B

Figure 32.1: Venn diagrams of some sets. The grey region represents the set labeled

at the bottom.

and more generally,

A ∩



i=1



i=1

(A ∩ B

A ∪



i=1



i=1

(A ∪ B

). (32.4)

32.1.2 Sample Space and Probability

The underlying concept in probability theory is the sample space,whichis

the same as the universal set of the set theory and is also denoted by S.Itis

the collection of all possible outcomes of an experiment. For example, for the

toss of a coin, S = {H, T }; for the toss of two coins, S = { HH,HT,TH,TT};

and for a die, S = {1, 2, 3, 4, 5, 6}.Anevent E is simply a subset of the

sample space. Thus, the event {HT,TH} is described as the outcome in

the toss of two coins, in which one of the coins is head; and { 2, 4, 6} is the

Event: elementary

and compound

event that the roll of a die produces an even number. An event, therefore,

can be elementary or compound, with the latter being a collection of the

former.

We are now ready to deﬁne probability. Since the sample space—which

Probability space

is sample space.

is now also called the probability space—includes all possible events, its

probability should be one, corresponding to absolute certainty. The probabil-

ity of any event (any subset of the probability space) has to be a nonnegative

number less than one. We may be tempted to say that the probability of

the union of two events is the sum of their probabilities, but that would be

wrong. For example, let S = {1, 2, 3, 4, 5, 6} be the universal set of a die,

and consider E

= { 1, 3, 5}, the odd outcomes, and E

= { 4, 5, 6},allout-

comes greater than 3. Intuitively, we know that the probability for each of

these two events is

.ButE

∪ E

= {1, 3, 4, 5, 6}, and if we were to add

probabilities for the union, we would get that the probability of {1, 3, 4, 5, 6}

is one, which is clearly wrong. The reason for this is that we have actu-

ally double-counted {5}, the intersection of the two sets. Only if the two

sets are disjoint, can we add the probabilities for the union. Now we deﬁne

probability:

32.1 Basic Concepts 785

Box 32.1.1. S is called a probability space if for each event E ⊂ S

there is a number P (E) satisfying the following conditions.

1. 0 ≤ P (E).

2. P (S)=1.

3. If E

and E

are disjoint events, then P (E

∪E

)=P (E

)+P (E

Example 32.1.1. In this example we derive some relations involving probabilities.

(1) If E

⊂ E

,thenP (E

) ≤ P (E

). To show this, use the ﬁrst equation in (32.2)

and the fact that E

∩ E

= E

to write

=(E

− E

) ∪ E

and P (E

)=P (E

− E

)+P (E

Since P (E

− E

) is nonnegative, we get P (E

) ≥ P (E

(2) P (E) ≤ 1 for every event E. This is a consequence of (1), because E ⊂ S and

P (S)=1.

(3) For any two events E

and E

P (E

∪ E

)=P (E

)+P (E

) − P (E

∩ E

). (32.5)

Use Equation (32.2) to write

P (E

)=P (E

− E

)+P (E

∩ E

P (E

)=P (E

− E

)+P (E

∩ E

), (32.6)

P (E

∪ E

)=P (E

− E

)+P (E

∩ E

)+P (E

− E

Substituting P (E

− E

)andP (E

− E

) of the ﬁrst two equations in the last

equation, we obtain the desired result.

Using E as E

and E

as E

, and noting that E −E

= E and E ∩ E

= ∅,the

ﬁrst (or second) equation in (32.6) gives P (E)=P (E)+P (∅), implying that

(4) P (∅)=0.

Using E as E

and E

as E

again, and noting that E −E

= E and E ∪E

= S,

the third equation in (32.6) and (4) give P (S)=P (E)+P (E

), implying that

(5) P (E

)=1−P (E).



Condition 3 of Box 32.1.1 can be generalized to the case of a collection of

mutually disjoint sets E

,...,E

P (E

∪E

∪... ∪E

)=P (E

)+P (E

)+···+ P (E



i=1

P (E

). (32.7)

A collection of mutually disjoint sets E

, ..., E

with S = E

∪E

∪...∪E

is called a partition of S. Such a collection has the property that partition of

universal set



i=1

P (E

)=1. (32.8)

786 Probability Theory

Up to now, we have not assigned any value to P (E)foragivensetE,and

it cannot be done without some further assumptions concerning the physical

properties of the probability space and the events that make it up. In fact,

if E

, ..., E

partition S, any set of nonnegative numbers p

, p

, ..., p

adding up to 1 with P (E

)=p

will satisfy the conditions of Box 32.1.1 and

will turn S into a probability space. Physically, however, certain choices will

not make sense. For instance, for S = { H, T }, the sample space of a single

coin, one can set P (H)=0.75 and P (T )=0.25. However, this assignment

is not very useful for ordinary coins, and in practice gives false results. For a

probability space composed of elementary events, it is often natural to assign

equal probability values to the elementary events. Thus if the E

of Equation

(32.8) are all elementary, then the natural assignment would be P (E

)=1/m

for i =1, 2,...,m. For a coin, m =2andP (H)=P (T )=0.5isanatural

choice, while for a die P (i)=1/6, and for a deck of cards, P (E

)=1/52.

32.1.3 Conditional and Marginal Probabilities

In many situations, the sample space is partitioned in two diﬀerent ways.

For example, a deck of cards can be partitioned either by 4 suits or by 13

values; the employees of a company can be partitioned by gender or by de-

partments in which they work. Suppose E

,...,E

and F

,...,F

are two collections of events that partition S. It should be clear that E

∩F

i =1, 2,...,m; j =1, 2,...,n is also a partition of S,andthat

j=1

∩ F

)=E

and

i=1

∩ F

)=F

. (32.9)

Since E

, F

,andE

∩F

are all partitions of S, we can deﬁne the proba-

bilities P (E

), P (F

), and P (E

∩ F

). Then, Equation (32.9) implies that

P (E



j=1

P (E

∩ F

)andP (F



i=1

P (E

∩ F

). (32.10)

P (E

)andP (F

) are called marginal probabilities.Marginal and

conditional

probabilities

Associated with the marginal probability is the conditional probability.

Suppose we know that E

has occurred. What is the probability of F

?For

example, we draw a card from a deck of cards and somebody tells us that it is

a heart. What is the probability that it is a jack? This conditional probability

is denoted by P (F

)andistheprobability of F

given that E

has occurred.

Example 32.1.2.

The best way to understand marginal and conditional proba-

bilities is to look at an example. Suppose that in a container, we have 100 marbles

coming in three diﬀerent sizes: small, medium, and large; and ﬁve diﬀerent colors:

white, black, red, green, and blue. Table 32.1 shows the distribution of the marbles

according to color and size.

First note that from the very deﬁnition of probability, the chance of getting a

medium red marble in a random drawing is 0.07, that of a large green marble is 0.03,

32.1 Basic Concepts 787

White Black Red Green Blue Total

Small 5 7 6 8 4 30

Medium 8 10 7 12 8 45

Large 9 5 4 3 4 25

Total 22 22 17 23 16 100

Table 32.1: The distribution of marbles according to size and color.

and there is a likelihood of 0.05 for drawing a small white marble. Similarly the

probability that on a random drawing from the container, the ball is black is 0.22,

and for the ball to be medium it is 0.45. This suggests the construction of another

table, Table 32.2, which shows the distribution of the probabilities according color

and size.

Each entry of the last row and last column of Table 32.2 is what we have called a

marginal probability. The conditional probability that the marble is small given that

its color is white is 5/22. This is because, by restricting the color to white, we limit

the number of marbles to 22 rather than 100. Similarly, the probability that the

marble is green given that its size is medium is 12/45; this also is a conditional prob-

ability. Conditional probabilities can be rewritten as ratios of probabilities. Thus,

the probability that the marble is small given that its color is white is 0.05/0.22,

and the second probability is 0.12/0.45.



The results of the foregoing example can be easily generalized. Let p

P (E

∩ F

), construct a table with m rows and n columns, and ﬁll the cells

with the numbers p

. Add one more row for the totals with entries P (F

P (F

), all the way to P (F

). Add one more column for the totals with entries

P (E

), P (E

), all the way to P (E

). It should now be clear that P (F

the probability of F

given that E

has occurred, is

P (F

P (E

∩ F

)

P (E

)

. (32.11)

Since any event and its complement partition the universal set, we can let

= A and F

= A

(only two F ’s), and write the equation above as

P (A|E

P (E

∩ A)

P (E

)

, (32.12)

White Black Red Green Blue Total

Small 0.05 0.07 0.06 0.08 0.04 0.3

Medium 0.08 0.1 0.07 0.12 0.08 0.45

Large 0.09 0.05 0.04 0.03 0.04 0.25

Total 0.22 0.22 0.17 0.23 0.16 1

Table 32.2: The distribution of probabilities according to size and color.

788 Probability Theory

or if we have two sets A and B and their complements as two partitions of S,

then

P (A|B)=

P (B ∩ A)

P (B)

, (32.13)

and this is true for any two sets.

If the probability P (A|B) does not depend on the event B in any way, i.e.,

if P (A|B)=P (A), then we say that the two events A and B are statistically

independent. Equation (32.13) now yields

Statistically

independent

events

P (A)=

P (B ∩ A)

P (B)

or P (A ∩B)=P (A)P (B), (32.14)

and the second equation becomes the deﬁnition for two events to be statisti-

cally independent.

It is important to diﬀerentiate between statistical independence and mu-

Diﬀerence

between statistical

independence and

mutual exclusion

tual exclusion. If two events are mutually exclusive then they have to be

statistically dependent since the occurrence of one precludes the occurrence

of the other. Similarly, Equation (32.14) shows that if P (A) > 0, P (B) > 0,

and A and B are statistically independent, then P (A ∩B) = 0, implying that

A ∩ B = ∅ and, therefore, that A and B cannot be mutually exclusive.

Equation (32.12) could be rewritten as

P (A ∩ E

)=P (E

)P (A|E

and since A ∩E

are mutually exclusive and their union is A,wehave[seethe

second equation in (32.10) with A = F

]

P (A)=



i=1

P (E

)P (A|E

). (32.15)

This is called Bayes’ theorem.

Bayes’ theorem

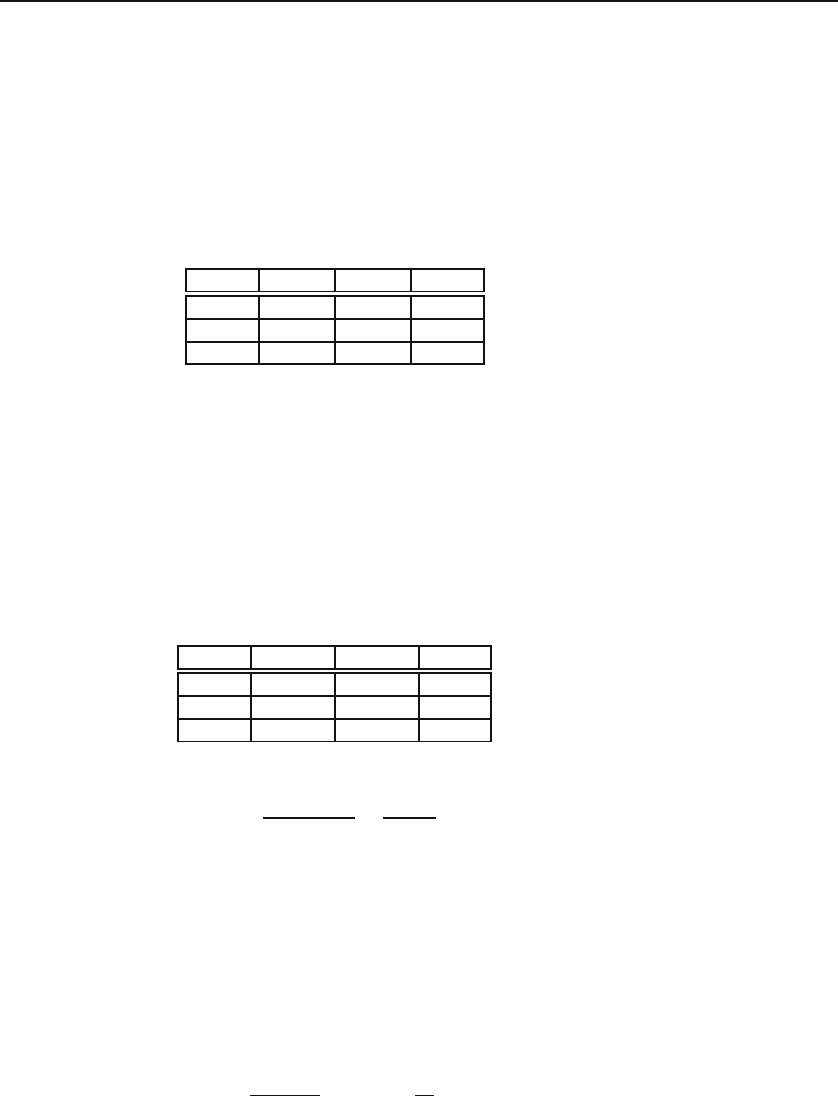
Example 32.1.3. A selective four-year college admits mostly students whose ACT

scores are 32 and higher, with a small number of admitted students whose scores are

below 32. The college has a graduation rate of 97%. Of those who graduate, 98%

have an ACT score of 32 and higher. Of those who drop out, 85% have an ACT

score below 32. We want to calculate the probability of graduation for a student

who has an ACT score below 32.

Let E

and E

denote the events corresponding, respectively to graduating and

dropping out. Let F

and F

denote the events corresponding to an ACT score of

32 or higher and lower than 32, respectively. We are after P (E

Consider the following table, in which the most obvious probabilities are entered:

Total

0.97

0.03

Total 1

32.1 Basic Concepts 789

Since we are given that P (E

)=0.97 and P (F

)=0.98, we can use Equation

(32.11) to ﬁnd the entry, p

, in the ﬁrst row and ﬁrst column:

= P (F

∩ E

)=P (E

∩ F

)=P (F

)P (E

)=0.98 × 0.97 = 0.9506.

The entry, p

, in the ﬁrst row and second column can now be calculated because

the total is given as 0.97:

= P (F

∩ E

)=0.97 − 0.9506 = 0.0194.

The table now looks like

Total

0.9506 0.0194 0.97

0.03

Total 1

We are also given that P (F

)=0.85. So, using Equation (32.11) again, we

can ﬁnd p

= P (F

∩ E

)=P (F

)P (E

)=0.85 × 0.03 = 0.0255.

The remaining entries are now trivial to calculate:

= P (F

∩ E

)=0.03 − 0.0255 = 0.0045,

P (F

)=0.9506 + 0.0045 = 0.9551,

P (F

)=0.0194 + 0.0255 = 0.0449,

and the complete table becomes

Total

0.9506 0.0194 0.97

0.0045 0.0255 0.03

Total 0.9551 0.0449 1

The desired probability is therefore,

P (E

∩ F

)

P (F

)

0.0194

0.0449

=0.432.

So, there is almost a 43% chance for the graduation of a student whose ACT score

is below 32.



32.1.4 Average and Standard Deviation

When we are given a set of values—say the scores of students in a class—and

asked to ﬁnd the average, we add the values and divide by the total number

of values. If {x

}

i=1

is the set of values, then the average ¯x is given by

¯x =



i=1



i=1





790 Probability Theory

This equation tacitly assumes that the probability is the same for all values

and equal to 1/N . If the probability depends on i, the deﬁnition of the average

has to take this into account. Let p

denote the probability for the occurrence

of x

, and change the notation for the average to the more common notation

whereby capital letters are used inside angle brackets. Then the average or

mean or expectation value of {x

}

i=1

is deﬁned asAverage,

expectation value,

mean

X =



i=1

. (32.16)

Another quantity of interest is the standard deviation,whichisamea-

Standard deviation

sure of how the values are spread from the mean. It is the average “distance”

between ¯x and x

. The obvious choice x

−¯x will have a zero average, because

it is both positive and negative and the deﬁnition of ¯x makes the positive and

negative values cancel. To avoid this cancellation, one takes the square of

these diﬀerences and then averages them. The variance σ

is deﬁned byVariance



i=1

− ¯x)

and the standard deviation by

σ =



i=1

− ¯x)

. (32.17)

When probability varies with x

, the deﬁnition of the variance changes to



i=1

−X)

. (32.18)

In many situations one may be interested in the average of a quantity that

depends on the random variable x

.Thus,ifg(x

) is such a quantity, one

writes

g(X) =



i=1

g(x

. (32.19)

In terms of such averages, one can show that

= X

−X

. (32.20)

Related to averages is the moment generating function deﬁned by

Moment

generating

function

e

 =



i=1

. (32.21)

The name comes from the fact that

e





t=0

= X

. (32.22)

32.1 Basic Concepts 791

32.1.5 Counting: Permutations and Combinations

The probability space of many situations is discrete. In fact, one can say

that all probability spaces are discrete, and only in the limit of large samples

(atoms and molecules in thermodynamics, for example) can one approximate

the random variable as a continuous variable. Therefore, it is important to

ﬁnd formulas that give the number of particular events of a universal set.

Suppose you have N distinguishable particles and you want to place

them in M bins. There are two cases that are used in practice: each bin

can hold as many particles as you place in it; or each bin can hold only one

particle. For each case, we are interested in ﬁnding the number of distinct

arrangements, or the number of conﬁgurations. Let this number be denoted

by Ω(N, M).

If there is no restriction on the occupancy number, then you have M

choices for the ﬁrst particle, M choices for the second particle, etc. Therefore,

(N,M)=M

. (32.23)

In statistical mechanics, this is called the Maxwell-Boltzmann statistics.

Maxwell-

Boltzmann

statistics

If the occupancy number is one, then you have M choices for the ﬁrst

particle, M − 1 choices for the second particle, etc. Therefore,

(N,M)=M(M −1)(M −2) ···(M − N +1)=

(M −N )!

,M>N.

(32.24)

This is called the permutation of M objects taken N at a time. If M = N,

Permutation

then Ω(N,N)=N! is simply called the permutation of N objects.

The elementary constituents of nature are indistinguishable or iden-

tical. How does this aﬀect the formulas above? Let’s consider the single-

occupancy case ﬁrst because it is easier. Equation (32.24) is overcounting the

arrangement by N! because a permutation of the particles does not give any

new arrangement. Therefore,

(N,M)=

N!(M −N )!

≡





,M>N. (32.25)

In statistical mechanics, this is called the Fermi-Dirac statistics.Itisalso

Fermi-Dirac

statistics

called the combination of M objects taken N at a time.

The multiple-occupancy case for indistinguishable particles is harder, but

there is a trick that can make it easier to derive the formula. Figure 32.2(a)

shows some bins with particles inside them. We can represent the arrangement

by placing the particles outside and to the right of the bins and represent the

bins by vertical lines as in Figure 32.2(b). Each vertical line has some particles

to its right and left except the bin on the extreme left, which has particles only

to its right. Since there is no limitation on the number of occupancy, the

number of arrangements can be calculated by permuting both the lines and

dots except the line on the extreme left. Since the dots are identical (as

are the lines), the problem reduces to ﬁnding the number of permutations of

792 Probability Theory

(b)(a)

Figure 32.2: (a) The bins with particles inside them. (b) Bins are represented by

vertical lines with the occupying particles to their right.

N + M − 1 objects N of which are identical and M − 1ofwhicharealso

identical, but diﬀerent from the other N. Therefore,

(N,M)=

(N + M − 1)!

N!(M −1)!



N + M − 1



. (32.26)

In statistical mechanics, this is called the Bose-Einstein statistics.

Bose-Einstein

statistics

32.2 Binomial Probability Distribution

The Fermi-Dirac statistics is closely related to the so-called binomial distri-

bution.EachoftheM bins has two states: either it is occupied or empty.

There are many situations where the binomial distribution applies. For exam-

ple, in tossing n coins, each coin can be a head or a tail; a quantum mechanical

spin-half particle can have its spin “up” or “down;” in a binary alloy system

each site of the alloy can be occupied by an atom A or B.

In fact, the binomial distribution is more general than this. In any trial,

Universality of

binomial

distribution

one can talk about success and failure, where success refers to one particular

outcome (out of the many possible outcomes), and failure to the rest of the

possible outcomes. Thus, if we are after a 6 in a toss of a die, then getting a

6 is a success, and getting 1, 2, 3, 4, or 5 is a failure.

Let p be the success probability, then the failure probability is q =1−p.

What is the probability P (m, n)thatinn trials we have m successes? Be-

cause the events are statistically independent (what happens in each trial is

independent of what has happened and what will happen), by (32.14), the

probabilities multiply. Thus the probability of m successes and n −m failures

is p

n−m

; and since there are





ways that this can happen in n trials,

the probability P (m, n)ofm successes in n trials is

P (m, n)=





n−m

m!(n − m)!

n−m

. (32.27)

Using the Stirling approximation x! ≈

√

2πe

−x

x+1/2

of Equation (11.6), the

reader can show that

P (m, n) ≈ 2



nπ

−(n−2m)

/2n

n−m

, (32.28)

assuming that both m and n − m are large, which is true in almost all cases

of large systems.