Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

32.2 Binomial Probability Distribution 793

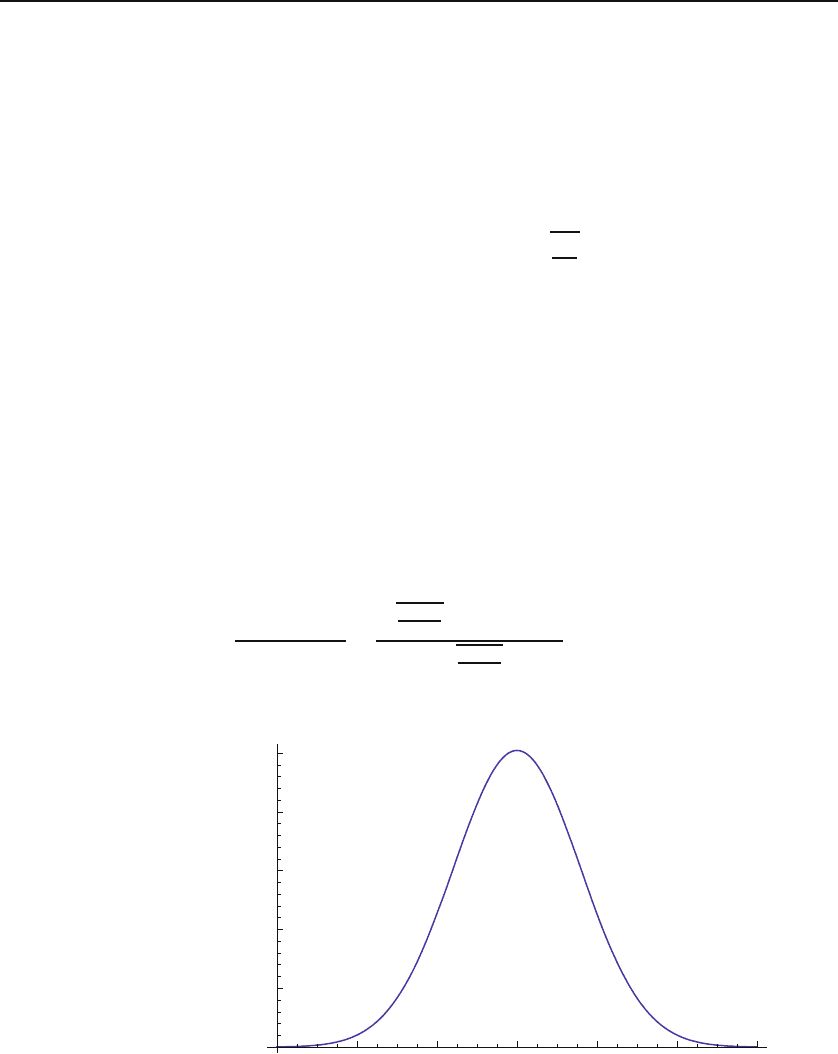
The special case of p = q =

is of importance:

P (m, n)=

m!(n − m)!2

≈



nπ

−(n−2m)

/2n

. (32.29)

Sometimes (32.28) is written in terms of the diﬀerence s between the number

of successes and failures. This is conveniently equal to 2m − n which is the

exponent of the exponential. We call s the success excess. Thus, (32.28)

becomes

P (s, n) ≈



nπ

−s

/2n

, Ω

(s, n)=2

P (s, n)=2



nπ

−s

/2n

(32.30)

where Ω

is the number of conﬁgurations now written in terms of s.

For the binomial distribution we can easily ﬁnd the moment generating

function. From its deﬁnition, we have

e

 =



x=0

P (x, n)=



x=0





n−x



x=0





(pe

)

n−x

=(pe

+ q)

, (32.31)

the last equality following from the binomial theorem. Equation (32.31) allows

us to easily calculate the average and variance for the binomial distribution.

First note that

e

 = npe

(pe

+ q)

n−1

e

 = npe

(q + npe

)(pe

+ q)

n−2

Now evaluate these at t = 0—and note that p + q =1—toobtain

X = np, X

 = n

+ npq, σ

= X

−X

= npq. (32.32)

Example 32.2.1.

Assume that the probability at birth that the newborn is male

(or female) is

. What is the probability that in a household of six, three are male?

Blind intuition tells us that the probability is

; but that is wrong! Rephrasing the

question to “What is the probability that in six trials we get three successes?” leads

us to the binomial distribution and the following answer:

P (3, 6) =

3!3!









6−3

3!3!





=0.3125.

This result may be surprising, but even more surprising is the result we obtain

if we ask the same question about a (small) school: “What is the probability that

in a school with 200 pupils, 100 are male?”

P (100, 200) =

200!

100!100!





100





200−100

200!

100!100!





200

=0.056.



794 Probability Theory

The surprise encountered in the preceding example is due to the confusion

caused by mixing the expected value with its probability. In a binomial distri-

bution, the expected value (or the mean or average) X = np,orX = n/2

when p =0.5, which is the answer we intuitively gave to the two questions in

the example above. Since our surprise increases with n, let us investigate the

behavior of the binomial distribution for values of m close to the mean for

very large n.

For large n and m, we can use (32.29), from which we obtain

P (n/2,n) ≈



nπ

This shows that P (n/2,n) → 0asn →∞. Thus the probability of having

n/2 successes in n trials becomes negligible as the number of trials increases.

But this is the maximum probability! Therefore, any other probability goes

to zero even faster. Where have all the probabilities gone?

Consider the graph of (32.29) for large n and plot it to a scale such that

the peak of the maximum, although small, is conspicuous. Figure 32.3 shows

such a graph for n = 1000. Note that the maximum probability has a value of

only 0.025, and that the graph drops to a value that is indistinguishable from

zero at about m = 560 on the right and m = 440 on the left. We can actually

calculate the ratio r of the small probability at m = 560 to the maximum at

m = 500 using (32.29):

r ≡

P (560, 1000)

P (500, 1000)



1000π

−(−120)

/2000



1000π

= e

−(−120)

/2000

=0.00075.

460 480 500 520 540 560

0.005

0.010

0.015

0.020

0.025

Figure 32.3: The plot of the binomial probability distribution for n = 1000.

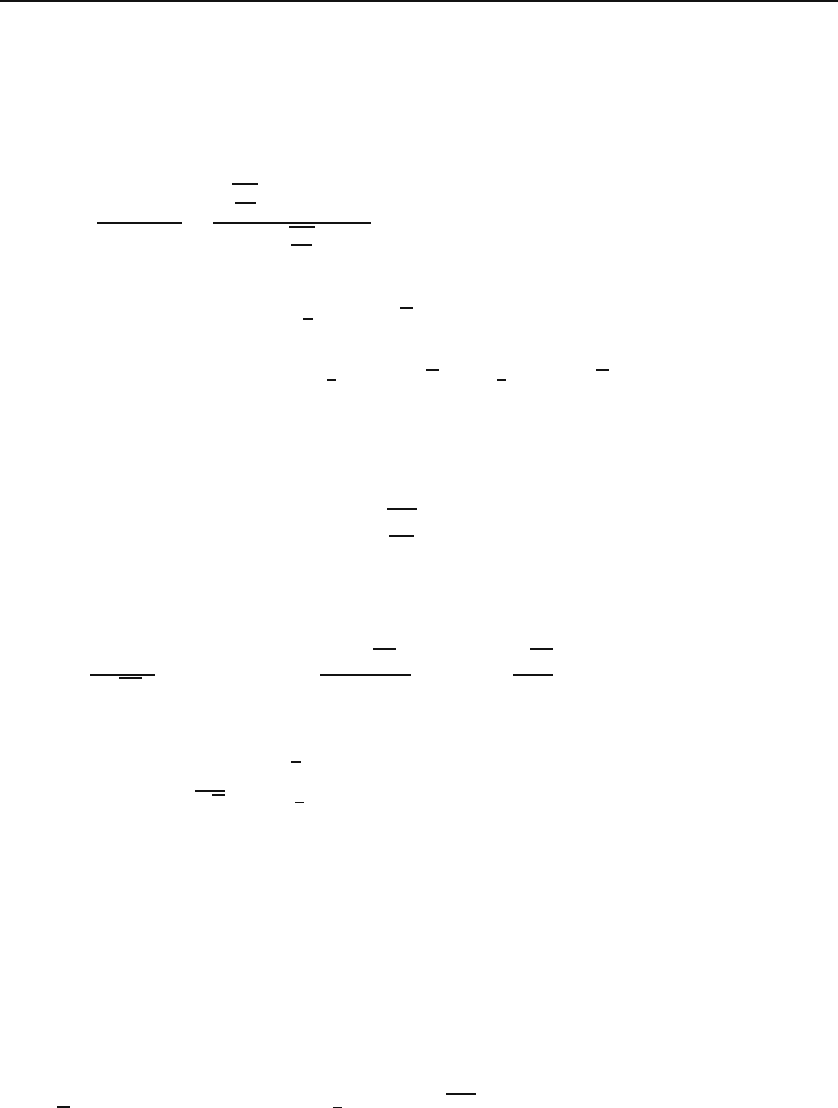
32.2 Binomial Probability Distribution 795

This same ratio is obtained if we use m = 440, and we can therefore conclude

that the nonzero probabilities are essentially concentrated between m

−

= 440

and m

= 560 for n = 1000.

Now let’s turn to a general n and ﬁnd the corresponding values of m

−

and

. These are the values of m at which the probability drops to 0.00075 of

its maximum value. To ﬁnd m

,wehavetosolvetheequation

r ≡

P (m, n)

P (n/2,n)



nπ

−(n−2m)

/2n



nπ

= e

−(n−2m)

/2n

=0.00075.

The answer is

(n ±3.8

√

n), (32.33)

as the reader may verify. So for a general n, a large fraction of the total

probability is concentrated between

(n − 3.8

√

n)and

(n +3.8

√

n). But

how much? What is the probability that the number of successes lies between

−

and m

To answer this question, we have to add all probabilities between m

−

and

. For large numbers, one can replace the sum with an integral:

P (m

−

≤ m ≤ m

,n)=

−



nπ

−(n−2m)

/2n

dm.

Deﬁne a new variable of integration x so that the exponent of the integrand

becomes −x

. This means

n − 2m

√

= x, or m =

n −

√

2nx

,dm= −

√

dx,

and the integral in terms of x becomes

√

3.8/

√

−3.8/

√

−x

dx =0.999855,

with the last result obtained by numerical integration. Therefore,

P (m

−

≤ m ≤ m

,n)=0.999855, (32.34)

which is interestingly independent of n.

Let us investigate the meaning of this result. It says that for very large n,

99.99% of the time the successes lie between m

−

and m

, and the probability

of not getting a success between m

−

and m

is only 0.0145%. Note also

that when n gets large, m

−

and m

become very nearly equal to n/2. For

example, if n =10

,then

=5×10

and m

(10

+3.8

√

)=5.001 ×10

796 Probability Theory

So the probabilities are concentrated in a very narrow interval; i.e., the prob-

ability curve is extremely sharp.

Going back to the probability of the male gender, we note that in a very

populous country such as China or India with approximately 10

inhabitants,

although the probability that exactly half the population is male is extremely

small, and of the order of



nπ



=0.000025,

the probability of the male population deviating too far from half is also

small. So although the exact success (half male) is highly unlikely, a number

of successes very close to exact is almost certain.

Example 32.2.2.

An isolated spin-

particle has equal probability of being in

either spin-up or spin-down states. If there are n such particles, then the probability

of m of them being in the up state is given by (32.29) or (32.30).

When a spin-

particle with magnetic moment μ is placed in a magnetic ﬁeld

B, it has two possible states: in the direction of the ﬁeld (called up)andopposite

to it (called down). In the ﬁrst case the energy of the particle is −μB andinthe

second case +μB. The energy of the system is therefore determined by the success

excess s, which in the present context is called the spin excess.

Now suppose that you have two systems that can exchange energy between

themselves with the combined system isolated. This means that the total energy

of the system is conserved. This energy is determined by the total spin excess s.

Let Ω

) be the conﬁguration number of the ﬁrst system and Ω

)for

the second. Let Ω

(s, n) be the number of conﬁgurations for the combined system,

where n = n

+ n

and s = s

+ s

is a constant. Since the total conﬁguration

number is the product of the conﬁguration number of the components, we have

(s, n)=Ω

)Ω

(s − s

)=C exp



−

(s − s

)



, (32.35)

where C is independent of s

What is the equilibrium state of the system? This corresponds to the most prob-

able state of the combined system, i.e., the state that maximizes Ω

(s, n). Instead

of maximizing Ω

, let’s maximize its logarithm, which is

ln Ω

=lnC −

−

(s − s

)

Diﬀerentiating with respect to s

,weget

∂ ln Ω

∂s

= −

s − s

. (32.36)

Note that the second derivative is

−





32.3 Poisson Distribution 797

which is negative, so the extremum is a maximum. Setting (32.36) equal to zero

yields the most probable conﬁguration: Condition for

thermal

equilibrium

ˆs

s − ˆs

ˆs

where the last equality follows from the previous ones (see Problem 32.13) and a

caret on a quantity indicates its value at maximum. If we substitute these in (32.35),

we get the maximum number of conﬁgurations:

max

(s, n)=C exp



−

ˆs

−

ˆs



= Ce

−s

/2n

. (32.37)

The veriﬁcation of the last equality is the subject of Problem 32.14.

Once in equilibrium, how likely is it for the system to move away from it? To

investigate this, let s

and s

be slightly diﬀerent from their equilibrium values

=ˆs

+ δ, s

= s − s

= s − ˆs

− δ =ˆs

− δ.

Substituting these in (32.35) yields

C exp



−

ˆs

+2ˆs

δ + δ

−

ˆs

− 2ˆs

δ + δ



=Ω

max

(s, n)exp



−

2ˆs

δ + δ

2ˆs

δ − δ



But ˆs

=ˆs

. Therefore,

(ˆs

+ δ, n

)Ω

(ˆs

− δ, n

)

max

(s, n)

=exp



−



. (32.38)

As a realistic numerical example, let n

= n

=10

and δ =10

so that the

fractional deviation δ/n

=10

−10

, a very small number. Then, the ratio in (32.38)

is e

−1000

=5× 10

−435

. The probability for fractional deviations larger that 10

−10

is smaller than e

−1000

. Assuming equal probability and adding the terms (about n

How likely is it for

the system to

abandon its

equilibrium state?

of them), the upper bound for the total probability becomes n

−1000

or 5 ×10

−412

times the probability of ﬁnding the system in equilibrium.

What is the meaning behind the statement “the probability to ﬁnd the sys-

tem with a fractional deviation larger than 10

−10

is 5 × 10

−412

of the probabil-

ity of ﬁnding the system in equilibrium?” To have a reasonable chance of ﬁnding

the system in such a deviated state, we have to sample 5 × 10

412

similar systems.

Even if we could sample at the rate of 10

systems per second, we would have

to sample for 5 × 10

400

seconds,orover10

393

years, or 10

383

times the age of the

universe! Therefore, it is safe to say that deviations described above will never be

observed.



32.3 Poisson Distribution

Poisson processes are famous results in the probability theory. A Poisson

process occurs in circumstances under which an event is repeated at a constant

rate of probability. Suppose that dt is so small that the probability of the

occurrence of two or more successes is negligible. Then the probability P

(dt)

of one success in dt is νdt,whereν is a constant.

798 Probability Theory

We are interested in P

(t), the probability of n successes in a time interval

t. We can obtain a recursive diﬀerential equation involving P

(t)andP

n−1

(t),

which we hope to solve to get P

(t). Consider P

(t + dt), the probability that

n successes occur in time t+dt. This can be written as the sum of two disjoint

probabilities, each consisting of the product of two independent probabilities:

(a) n successes occur in time t and none in time dt,(b)n −1 successes occur

in time t and one in time dt.Insymbols,

(t + dt)=P

(t)P

(dt)+P

n−1

(t)P

(dt).

But P

(dt)=νdt and P

(dt)=1−P

(dt)=1−νdt. Therefore,

(t + dt)=P

(t)(1 −νdt)+P

n−1

(t)νdt.

Expanding the left-hand side as P

(t + dt)=P

(t)+

dt and dividing

both sides by dt, we obtain the desired recursive DE:

(t)

+ νP

(t)=νP

n−1

(t). (32.39)

For n =0theright-handsideiszeroandtheDE

(t)

+ νP

(t)=0

has the solution P

(t)=Ae

−νt

. The fact that the probability of no success

in zero time interval is 1 yields A =1.

Equation (32.39) is a ﬁrst order DE which can be solved. In fact, the

solution is given in Theorem 23.3.1, where in the case at hand

μ(t)=exp



νdt



= e

νt

and

(t)=

νt



C + ν

νt

n−1

) dt



We must have P

(0) = 0 because there is no chance that n successes can

be achieved in zero time interval. This sets C = 0, and we get the integral

recursion relation:

(t)=νe

−νt

νt

n−1

) dt

. (32.40)

Substitute for P

n−1

)asanintegralofP

n−2

to get

(t)=νe

−νt

νt

(

νe

−νt

νt

n−2

) dt

)

(t)=ν

−νt

νt

n−2

) dt

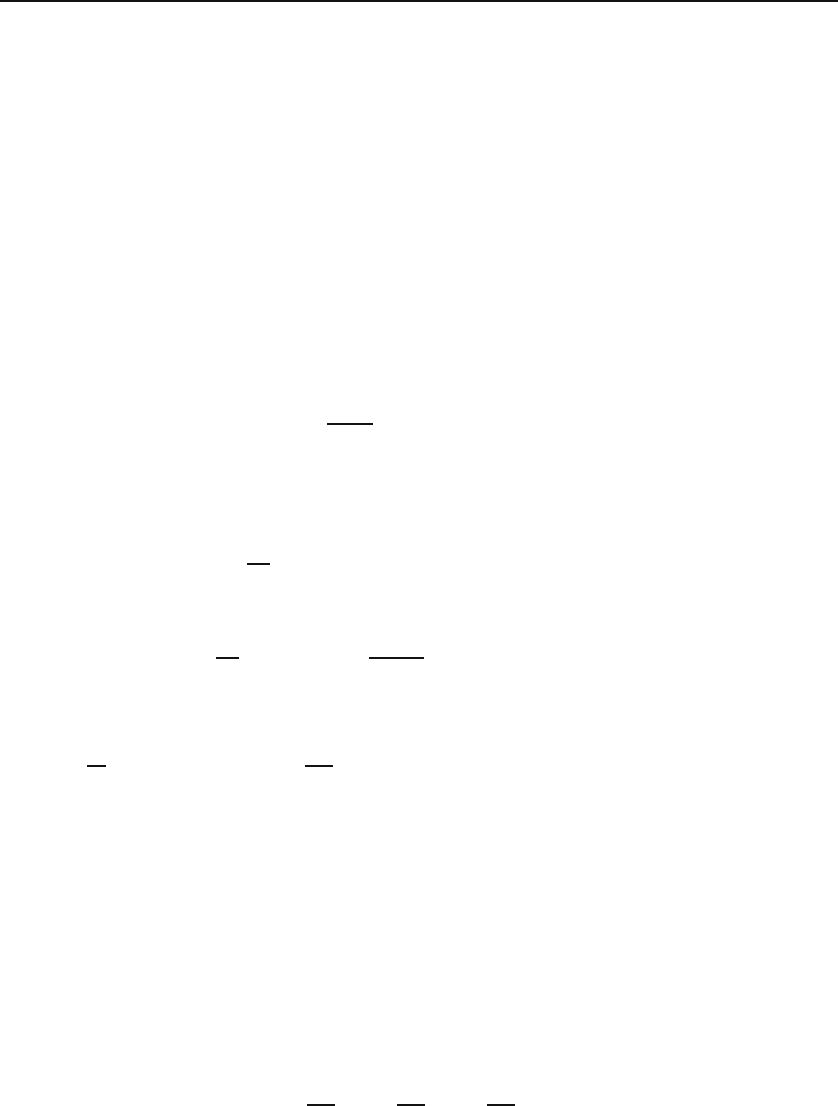
32.3 Poisson Distribution 799

It should now be clear that if we repeat this k times, we get

(t)=ν

−νt

···

k−2

k−1

νt

n−k

) dt

k−1

··· dt

In particular when k = n,

(t)=ν

−νt

···

n−2

n−1

νt

) dt

n−1

··· dt

But P

(t)=e

−νt

so P

)=e

−νt

, and the above equation becomes

(t)=ν

−νt

···

n−2

n−1

··· dt

. (32.41)

Starting with the innermost integral over t

and integrating all the t’s, the

reader can show that the result will be t

/n!. We thus ﬁnally obtain the

Poisson process

(t)=

(νt)

−νt

. (32.42)

Poisson process is naturally a time-dependnent process and ν is the rate or

the frequency of that process.

The discrete Poisson distribution p(n) is deﬁned by setting νt = λ to

obtain

Poisson probability

distribution

p(n)=

−λ

,n=0, 1, 2,...,∞. (32.43)

The moment generating function is

e

 =

∞



x=0

−λ

= e

−λ

∞



x=0

(λe

)

= e

λ(e

−1)

. (32.44)

This gives

e

 = λe

λ(e

−1)

e

 = λe

λ(e

−1)

(λe

+1).

Evaluating these at t =0yields

X = λ, X

 = λ(λ +1),σ

= X

−X

= λ. (32.45)

Example 32.3.1.

A city had 24 major ﬁre accidents in a year. What is the

probability that there will be (a) one major ﬁre next month, (b) at least 5 major

ﬁres in the next 6 months?

Here ν, the frequency of ﬁre is 24 per year or 2 per month. So for (a) we have

λ =2×1=2and

p(1) = λe

−λ

=2e

−2

=0.27.

For (b), λ =2×6 = 12 and

p(n ≥ 5) = 1 −p(0) −p(1) − p(2) − p(3) − p(4)

=1−e

−12

− 12e

−12

−

−12

−

−12

−

−12

=0.992.



800 Probability Theory

Example 32.3.2. In a department store, 39 light bulbs burn out per year. The

light bulbs are replaced from the store stock, which is replenished every week. What

is the minimum number of light bulbs the stock should hold so that the store will

have all its light bulbs working with a probability of at least 99%?

The frequency is ν =39/52 = 0.75 per week. Thus, λ =0.75 × 1=0.75. Let

n stand for the number of bulbs burnt per week and m the number of bulbs in the

stock. Then the store will have all its lights on as long as n ≤ m. Therefore, we

want p(n ≤ m) ≥ 0.99. This gives

p(n ≤ m)=



n=0

−λ

≥ 0.99,

p(n ≤ m)=



n=0

(0.75)

≥ 0.99e

0.75

=2.096,



1+0.75 +

0.75

+ ···+

0.75



≥ 2.096.

By trial and error, the reader can verify that m =3.



Poisson distribution is the limiting case of the binomial distribution when

n →∞, p → 0, and λ = np is constant. To see this, expand n!/(n −m)! using

the Stirling approximation:

(n −m)!

≈

√

2πe

−n

n+1/2

√

2πe

−n+m

(n −m)

n−m+1/2

= e

−m



n − m



n+1/2

(n − m)

Now note that



n − m



n+1/2

≈



n −m



(1 −m/n)

→

−m

= e

and (n − m)

≈ n

.Furthermore,

n−m

=(1−p)

n−m



1 −



n−m

≈



1 −



→ e

−λ

Substituting all this in (32.27) yields

P (m, n) → n

−λ

(np)

−λ

which is the Poisson distribution p(m).

Example 32.3.3.

A 3000-letter long message has been transmitted electronically

with an error probability of 10

−3

. What is the probability that there are at least

two errors in the message?

This is a binomial distribution (error is success!) with small probability and large

n. Therefore, we can use Poisson distribution (32.43) with λ = np = 3000×10

−3

=3.

Then

p(n ≥ 2) = 1 − p(0) − p(1) = 1 − e

−3

− 3e

−3

=0.8.

The probability that there is exactly one error in the message is

p(1) = 3e

−3

=0.149.



32.4 Continuous Random Variable 801

32.4 Continuous Random Variable

Most probability sample spaces are so large that approximating the discrete

events with continuous variables becomes very useful and accurate. Take the

case of the binomial distribution discussed above. We started with discrete

counting, but when our sample grows to 10

, not only does the discrete sum

become unmanageable, it becomes unnecessary as well. This is also reﬂected

in the replacement of the strictly discrete factorial with the more adaptable

exponential function through the use of the Stirling approximation.

When continuous variables are used, probability is described by proba-

bility density. In the case of a single random variable x, the probability

Probability density

density f (x) is used to give the probability that x lies in an interval of length

dx:

P (x − dx/2 <x<x+ dx/2) = f(x) dx,

f(x) dx =1,

where (a, b) is the interval for which x is deﬁned. This interval can be taken

to be (−∞, ∞) by assigning zero probability density to points on the left of

a and on the right of b. The integral describes the total probability, which is

1 as in the case of the discrete variable.

For more variables, the generalization is clear. If x =(x

,...x

)and

the probability density function is f (x), then the probability that x is in an

inﬁnitesimal m-dimensional volume d

x is

P (x ∈ d

x)=f(x) d

f(x) d

x =1, (32.46)

where Ω is the region for which f(x) is deﬁned. If V is a subset of Ω, then

P (x ∈ V )=

f(x) d

gives the probability that x lies in V .

For example, a quantum mechanical wave function Ψ(r)givesrisetoa

density f(r)=|Ψ(r)|

, and all wave functions are normalized so that

|Ψ(r)|

x =1 and P (r ∈ V )=

|Ψ(r)|

x, (32.47)

where r is a set of convenient coordinates.

The average and variance is deﬁned in exactly the same way. For example,

the average of the ith component of x, denoted by X

,isgivenby

X

 =

f(x) d

x. (32.48)

Similarly

−X

)

f(x) d

x, (32.49)

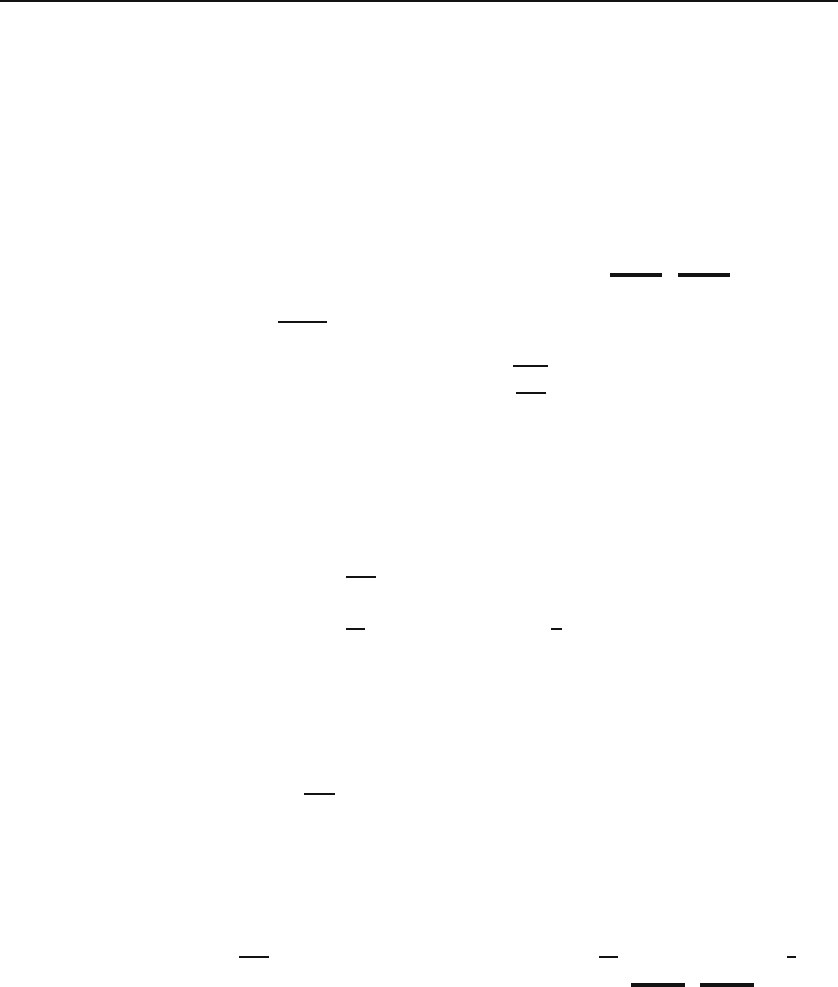
802 Probability Theory

and

g(X) =

g(x)f(x) d

x. (32.50)

Example 32.4.1.

The ground state of the hydrogen atom is described in spherical

coordinates by the wave function Ae

−r/a

,wherea

is the Bohr radius, A is a

constant to be determined by the normalization (32.47), and r is the distance of the

electron to the nucleus, which is placed at the origin. Using the volume element in

spherical coordinates, we have

1=A

∞

2π

−2r/a

sin θdrdθdϕ=4πA

∞

−2r/a



 

= πA

giving A =



1/πa

.Thusthenormalized wave function for the ground state of the

hydrogen atom is

Ψ(r, θ, ϕ)=

πa

−r/a

with |Ψ(r, θ, ϕ)|

being the probability density of ﬁnding the electron at (r, θ, ϕ).

From this, we can calculate, for instance, the probability that the electron ap-

proaches the nucleus to within 10% of the Bohr radius. The second equation in

(32.47) gives the answer where V is the volume of a sphere with radius 0.1a

Therefore,

P (r ∈ V )=

πa

0.1a

2π

−2r/a

sin θdr dθ dϕ

0.1a

−2r/a

dr =

0.2

−x

dx ≈ 0.0013,

where we used the change of variables r = a

x/2 in the last integral to turn it into

a numerical factor.

We can also calculate some averages. For instance, the average for the x coor-

dinate of the electron is (remember that x = r sin θ cos ϕ)

X =

πa

∞

2π

r sin θ cos ϕe

−2r/a

sin θdr dθ dϕ =0.

The result of zero being due to the ϕ integration. Similarly, Y  and Z also vanish.

This null result should be expected because it is just as likely for the electron to

have a positive x value as it is to have a negative value. On the other hand, r is

always positive, and we expect its average value to be nonzero. In fact,

R =

πa

∞

2π

−2r/a

sin θdr dθ dϕ =

∞

−2r/a



 

=3a



A random variable x

is said to be independent of the rest of the variablesIndependent

random variable

if the probability density f(x) factors out into

f(x)=g(x

)h(x

,...,x

α−1

α+1

,...,x

) ≡ g(x

(x),