Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

762 Nonlinear Dynamics and Chaos

one corresponding to an inﬁnite-cycle ﬁxed point, we conclude that, on a

bifurcation diagram, chaos will occur at

= α

∞

≡ lim

n→∞

. (31.17)

The limit in (31.17) is one way of characterizing chaos. A more direct way

is to look at the trajectories. Two nearby points starting at x

and x

+  will

be separated after n iterations by a distance

the n-th iterative

Lyapunov

exponent

≡



[n]

+ ) − f

[n]

)



If this separation grows exponentially, we have a chaotic behavior. We deﬁne

[n]

,thenth iterative Lyapunov exponent at x

,by

≡ d

[n]

≡ e

[n]

Then

[n]







⎧

⎨

⎩



[n]

+ ) − f

[n]

)





⎫

⎬

⎭

As  → 0, the RHS becomes the absolute value of the derivative of the n-th

iterate at x

. But by the chain rule

[n]



[n−1]

(x))



= f



[n−1]

)



 

n−1

)

[n−1]



= f



n−1

)

[n−1]



Using this relation repeatedly, we obtain

[n]



= f



n−1



n−2

) ...f



n−k

)

[n−k]



= f



n−1



n−2

) ...f



where in the last step we set k = n and noted that f

[0]

= f

. It now follows

that

[n]

ln [|f



)||f



)|···|f



n−1

)|]

which can also be written as

[n]

n−1



k=0

ln |f



)|. (31.18)

31.2 Systems Obeying DEs 763

It is common to deﬁne the local Lyapunov exponent as follows: local Lyapunov

exponent

≡ lim

n→∞

[n]

= lim

n→∞

n−1



k=0

ln |f



)|. (31.19)

To characterize the chaotic behavior of systems obeying iterated maps,

one has to calculate λ

for a sample of trajectory points and then take their

average. The result is called the Lyapunov exponent for the system. It

Lyapunov

exponent

turns out that

Box 31.1.5. A necessary condition for a system obeying an iterated map

function f

(x) to be chaotic for α is for its Lyapunov exponent to be

positive at α.

31.2 Systems Obeying DEs

As a paradigm of a nonlinear dynamical system, we shall study the motion

of a harmonically driven dissipative pendulum whose angle of oscillation is

not necessarily small. The equation of motion of such a pendulum, coming

directly from the second law of motion, is

= F

cos(Ωt) − b

− mg sin θ, (31.20)

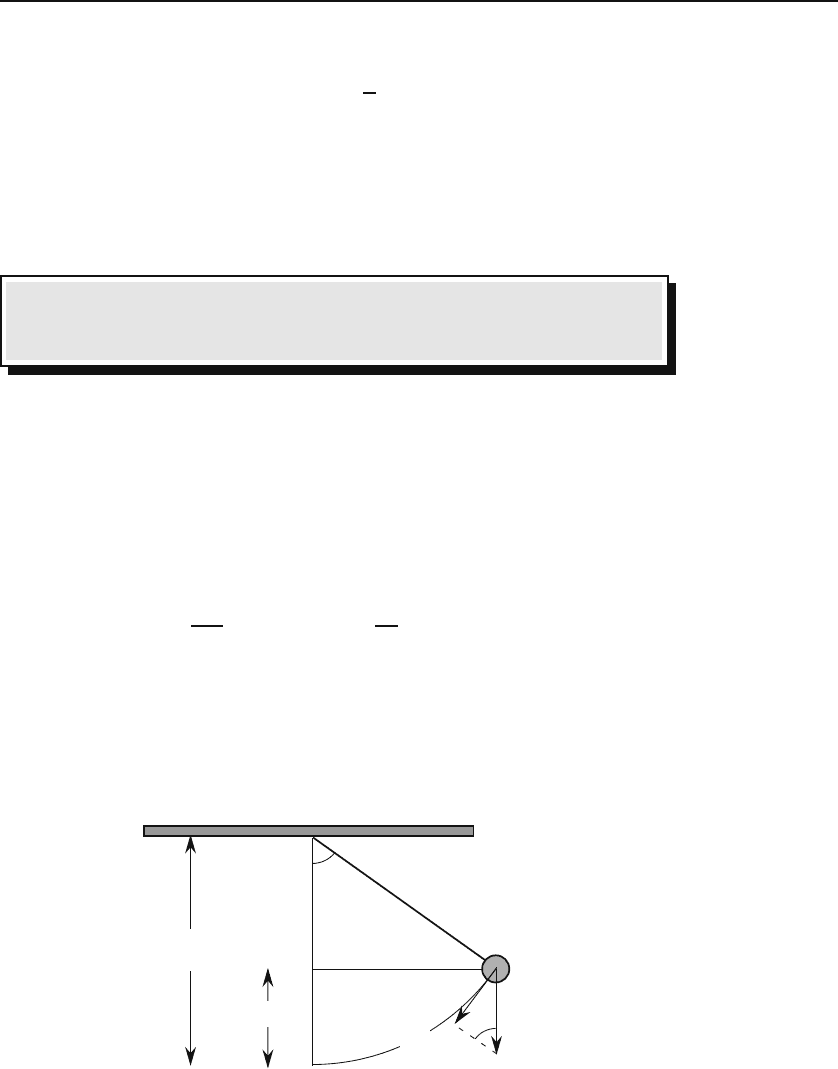
where x is the length (as measured from the equilibrium position) of the arc

of the circle on which mass m moves (see Figure 31.4).

The ﬁrst term on the RHS of Equation (31.20) is the harmonic driving

force with angular frequency Ω, the second is the dissipative (friction, drag,

etc.) force, and the last is the gravitational force in the direction of motion.

Figure 31.4: The displacement x and the gravitational force acting on the pendulum.

764 Nonlinear Dynamics and Chaos

The minus signs appear because the corresponding forces oppose the motion.

Since the pendulum is conﬁned to a circle, x and θ are related via x = lθ,and

we obtain

= F

cos(Ωt) − bl

dθ

− mg sin θ.

Let us change t to t = τ



l/g where τ is a dimensionless parameter measuring

time in units of T/(2π)withT being the period of the small-angle pendulum.

Then, with the dimensionless constants

γ ≡

,φ

≡

,ω

≡ Ω

the DE of motion becomes

dτ

+ γ

dθ

dτ

+sinθ = φ

cos(ω

τ).

It is customary to write this as

θ + γ

θ +sinθ = φ

cos(ω

t), (31.21)

where now t is the “dimensionless” time, and the dot indicates diﬀerentiation

with respect to this t.

31.2.1 The Phase Space

The study of dynamical systems—i.e., systems obeying DEs—is considerably

more complicated than systems obeying iterated maps. While in the latter

case we were able to use a fair amount of analytical tools, the discussion of

the former requires an enormous amount of numerical computation.

One of the devices that facilitates our understanding of dynamical systems

is the phase space diagram. The phase space of a dynamical system is a

phase space

diagram

Cartesian multidimensional space whose axes consist of positions and mo-

menta of the particles in the system. Instead of momenta the velocities of

particles are mostly used. Thus a single particle conﬁned to one dimension

(such as a particle in free fall, a mass attached to a spring, or a pendulum)

has a two-dimensional phase space corresponding to the particle’s position and

speed. Two particles moving in a single dimension have a four-dimensional

phase space corresponding to two positions and two speeds. A single par-

ticle moving in a plane also has a four-dimensional phase space because two

coordinates are needed to determine the position of the particle, and two com-

ponents to determine its velocity, and a system of N particles in space has a

6N-dimensional phase space.

A trajectory of a dynamical system is a curve in its phase space corre-

phase space

trajectory

sponding to a possible motion of the system. If we can solve the equations

Recall that T =2π



l/g.Soτ = t/(T/2π) is indeed dimensionless.

31.2 Systems Obeying DEs 765

of motion of a dynamical system, we can express all its position and velocity

variables as a function of time, constituting a parametric equation of a curve

in phase space. This curve is the trajectory of the dynamical system.

Let us go back to our pendulum, and consider the simplest situation in

which there is no driving force, the dissipative eﬀects are turned oﬀ, and the

angle of oscillation is small. Then (31.21) reduces to

θ + θ = 0, whose most

general solution is θ = A cos(t + α)sothat

≡ θ = A cos(t + α),

≡ ω ≡

θ ≡

dθ

= −A sin(t + α). (31.22)

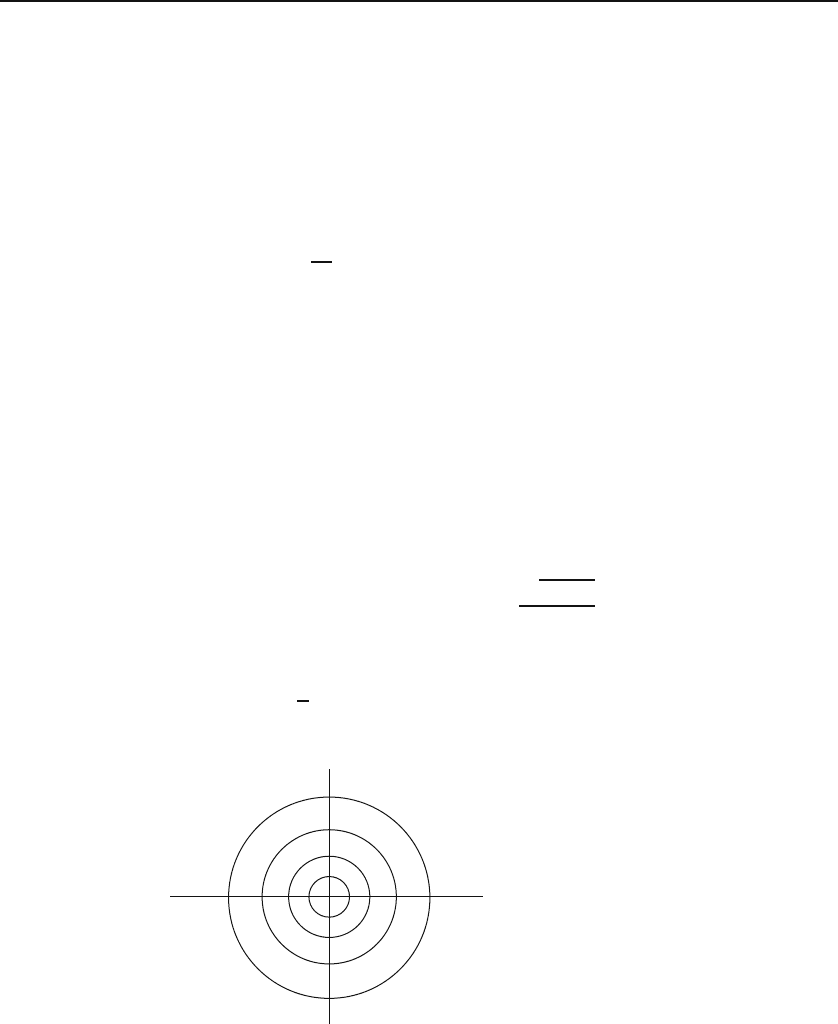
This is a one-dimensional system (there is only one coordinate, θ)withatwo-

dimensional phase space. Equation (31.22) is the parametric equation of a

circle of radius A in the x

-plane. Because A is arbitrary (it is, however,

determined by initial conditions), there are (inﬁnitely) many trajectories for

this system, some of which are shown in Figure 31.5.

Let us now make the system a little more complicated by introducing a

dissipative force, still keeping the angle small. The DE is now

θ + γ

θ + θ =0

and the general solution for the damped oscillatory case is

= θ(t)=Ae

−γt/2

cos(ω

t + α)whereω

≡



4 − γ

with

= ω =

θ = −Ae

−γt/2

cos(ω

t + α)+ω

sin(ω

t + α)

Figure 31.5: The phase space trajectories of a pendulum undergoing small-angle

oscillations with no driving or dissipative forces. Diﬀerent circles correspond to diﬀerent

initial conditions.

766 Nonlinear Dynamics and Chaos

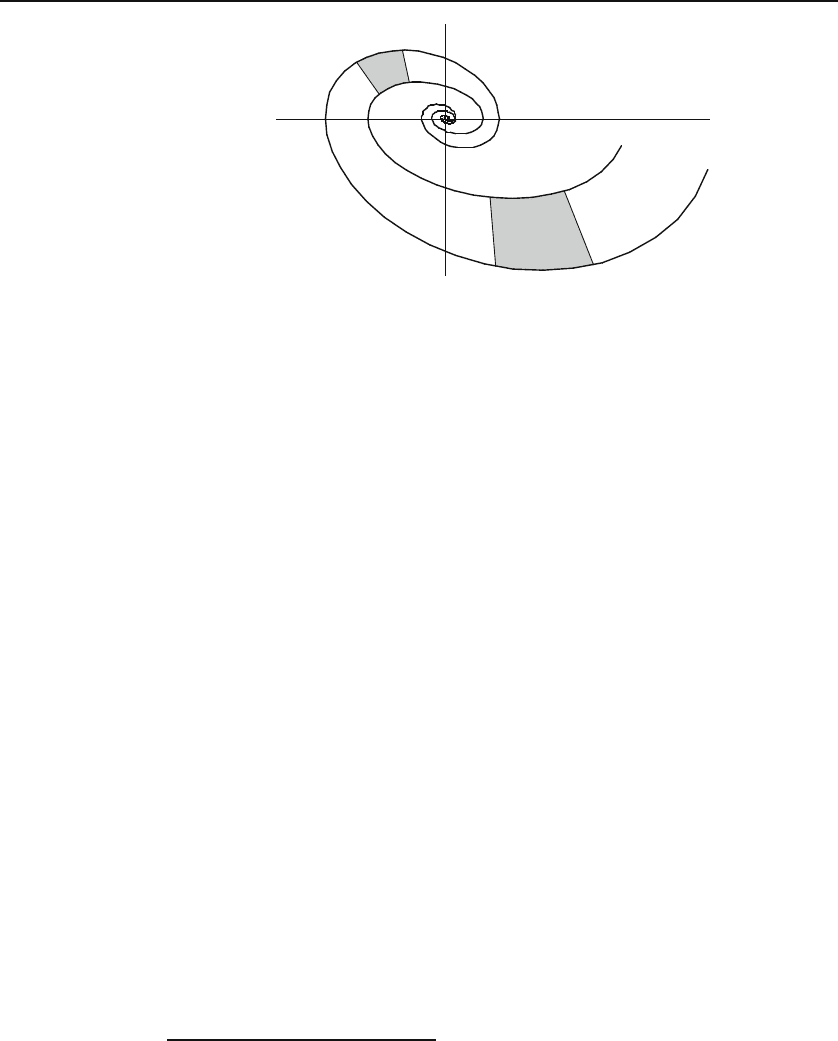
Figure 31.6: The phase space trajectories of a damped pendulum undergoing small-

angle oscillations with no driving force. Diﬀerent spirals correspond to diﬀerent initial

conditions. The larger shaded region, in time, shrinks to the smaller one.

The trajectories of this system are not as easily obtainable as the un-

damped linear oscillator discussed above. However, since the two coordinates

of the phase space are given in terms of the parameter t, we can plot the

trajectories. Two such trajectories for two diﬀerent A’s (but the same γ)are

shown in Figure 31.6.

A new feature of this system is that regardless of where the trajectory

starts at t = 0, it will terminate at the origin. The analytic reason for this is

of course the exponential factor in front of both coordinates which will cause

their decay to zero after a long time.

It seems that the origin “attracts” all

trajectories, and for this reason is called an attractor.

attractor

There are other kinds of attractors in nonlinear dynamics theory. For

example, if trajectories approach an arc of a curve, or an area of a surface,

then the curve or the area becomes the attractor. Furthermore, for a given

value of the parameter, there may be more than one attractor for a given

dynamical system (just as there were more than one ﬁxed point for iterated

maps); and it may happen that the trajectories approach these attractors only

for certain initial values of the dynamical variables. The set of initial values

corresponding to trajectories that are attracted to an attractor is called the

basin of attraction for that attractor. The set of initial values that lie on

basin of attraction

the border between the basin of attraction of two diﬀerent attractors is called

a separatrix.

separatrix

31.2.2 Autonomous Systems

Now we want to consider motion with large angles. The DE is then no longer

linear. The discussion of (nonlinear) DEs of higher orders is facilitated by

“Long” compared to 1/γ.

This is what we called a ﬁxed point in our discussion of iterated maps. However,

because of the existence of a variety of “ﬁxed objects” for dynamical systems, it is more

common to call these attractors.

31.2 Systems Obeying DEs 767

treating derivatives as independent variables. The deﬁning relations for these

derivativesaswellastheDEitselfgiveasetofﬁrst-order DEs. For example,

the third-order DE

= x

+sin(ωt − kx)

+ e

cos(ωt)

can be turned into three ﬁrst-order DEs by setting ˙x ≡ x

and ¨x ≡ x

.Then

the DE splits into the following three ﬁrst-order DEs:

˙x = x

, ˙x

= x

˙x

= x

+sin(ωt − kx)x

+ e

cos(ωt).

This is a set of three equations in the three unknowns x, x

,andx

,which,

in principle, can be solved.

It is desirable to have a so-called autonomous system of ﬁrst-order DEs. autonomous and

nonautonomous

dynamical systems

These are systems which have no explicit dependence on the independent

variable (in our case, t). Our equations above clearly form a set of nonau-

tonomous DEs. The nonautonomous systems can be reduced to autonomous

ones by a straightforward trick: One simply calls t a new variable. More specif-

ically, in the equation above, let x

≡ ωt. Then the nonautonomous equations

above turn into the following autonomous system:

˙x = x

, ˙x

= x

˙x

= x

+sin(x

− kx)x

+ e

cos x

˙x

= ω.

We have had to increase the dimension of our phase space by one, but in

return, we have obtained an autonomous system of DEs.

Based on the prescription above, we turn the second-order DE of the driven

pendulum into a set of ﬁrst-order DEs. First we rewrite the DE describing a

general pendulum [see Equation (31.21)] as

θ + γ

θ +sinθ = φ

cos α,

where α is simply ω

t. Then turn this equation into the following entirely

equivalent set of three ﬁrst-order DEs:

θ = ω, ˙ω = −γω −sin θ + φ

cos α, ˙α = ω

. (31.23)

The two-dimensional (θ, ω) phase space has turned into a three-dimensional

(θ, ω, α) phase space. But the resulting system is autonomous.

Just as in the linear case, it is instructive to ignore the damping and driving

forces ﬁrst. We set γ and φ

equal to zero in Equation (31.23) and solve the set

of DEs numerically.

For small angles, we expect a simple harmonic motion

The solution can be given in terms of elliptic functions as discussed in Chapter 11.

768 Nonlinear Dynamics and Chaos

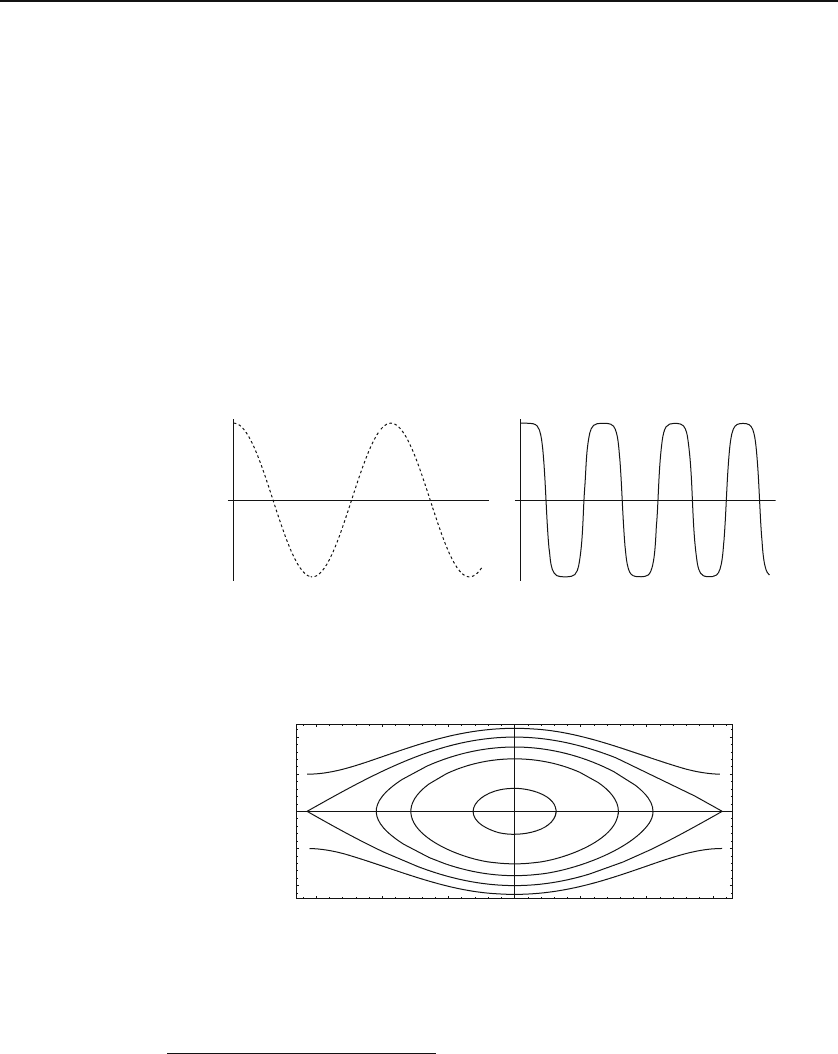
(SHM). So, with θ(0) = π/10 and ω(0) = 0,

we obtain the plot on the left of

Figure 31.7. This plot shows a simple trigonometric dependence of angle on

time.

The initial angular displacement of the plot on the right of Figure 31.7 is

approximately π radians corresponding to raising the mass of the pendulum

all the way to the top.

The ﬂattening of curves at the maxima and minima

of the plot indicates that the pendulum almost stops once it reaches the top

and momentarily remains motionless there. This is expected physically as

θ(0) = π is a location of (unstable) equilibrium, i.e., with ω(0) = 0, the

pendulum can stay at the top forever. So, for θ(0) ≈ π, the pendulum is

expected to stay at the top, not forever, but for a “long” time.

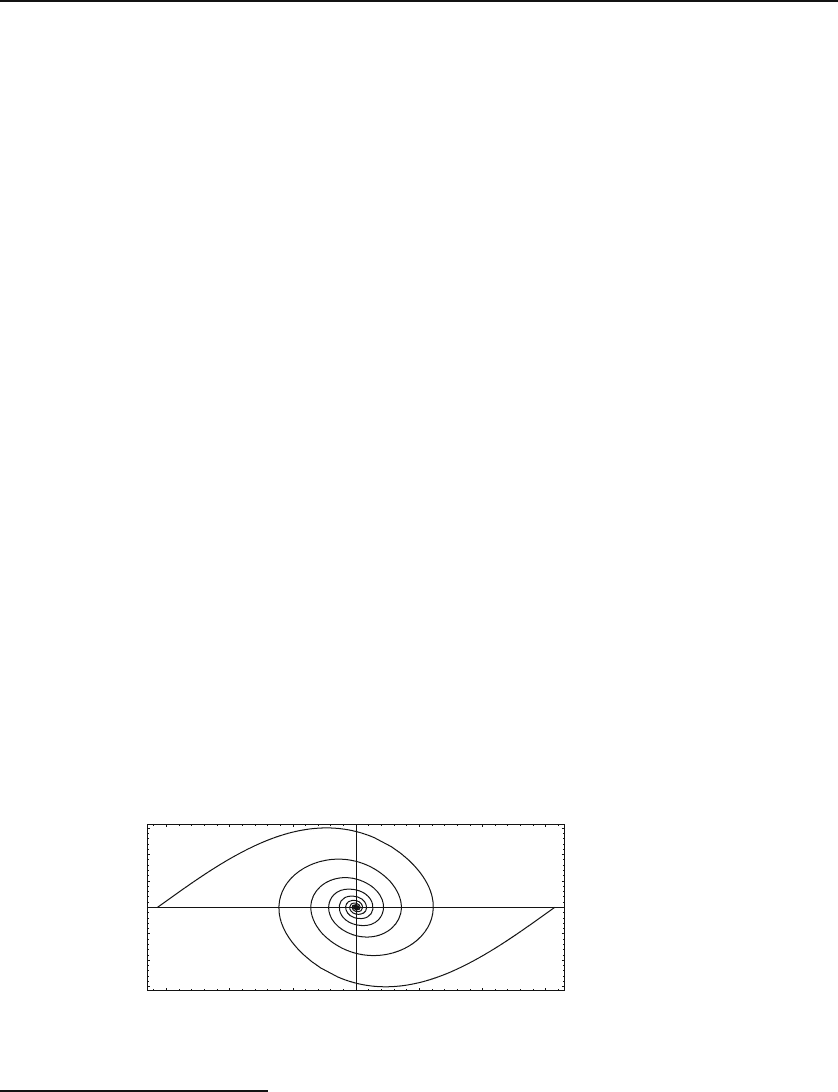
The phase space diagram of the pendulum can give us much information

about its behavior. With the initial angular velocity set at zero, the pendulum

will exhibit a periodic behavior represented by closed loops in the phase space.

Figure 31.8 shows four such closed loops corresponding—from small to large

Figure 31.7: The undamped undriven pendulum shows an SHM for small initial angles

(the plot on the left has a maximum angle of π/10). For large angles, the motion is

periodic but not an SHM. The maximum angle of the plot on the right is slightly less

than π.

–3 –2 –1 0 1 2 3

–2

–1

Figure 31.8: Phase space diagrams for a pendulum corresponding to diﬀerent values

of maximum displacement angles (horizontal axis). The inner diagrams correspond to

smaller values; the outermost plot has a maximum angle of 179.98 degrees at which the

angular speed is 1.

It is important to keep ω(0) small, because a large initial angular velocity (even at a

small initial angle) can cause the pendulum to reach very large angles!

For this to be possible, clearly the mass should be attached to a rigid rod (not a string)!

31.2 Systems Obeying DEs 769

loops—to the initial angular displacement of π/5, π/2, 2π/3, and (almost) π.

These loops represent oscillations only: the angular displacement is bounded

between a minimum and a maximum value determined by θ(0). The closed

loops are characterized by the fact that the angular speed vanishes at maxi-

mum (or minimum) θ, allowing the pendulum to start moving in the opposite

direction.

The outermost curves result from θ(0) = −π, ω(0) = 1 (the upper curve),

and θ(0) = π, ω(0) = −1 (the lower curve), and represent rotations.Thean-

gular displacement is unbounded: it keeps increasing for all times. Physically,

this corresponds to forcing the pendulum to “go over the hill” at the top by

providing it an initial angular velocity. If the pendulum is pushed over this

hill once, it will continue doing it forever because there is no damping force.

The rotations are characterized by a nonzero angular velocity at θ = ±π.This

is clearly shown in Figure 31.8.

What happens when the damping force it turned on? We expect the tra-

jectories to spiral into the origin of the phase space as in the case of the linear

(small-angle) pendulum. Figure 31.9 shows two such trajectories correspond-

ing to an initial displacement of just below π (on the right), and just above

−π (on the left). For both trajectories, the initial angular velocity is zero. It

is intuitively obvious that regardless of the initial conditions, the pendulum

will eventually come to a stop at θ = 0 if there are no driving forces acting

on it. So, Figure 31.9 is really representative of all dissipative motions of the

pendulum.

The origin of the phase space is a ﬁxed point of the pendulum dynamics.

But it is not the only one. In general, any point in the phase space for which

the time derivative of all coordinates of the trajectory are zero is a ﬁxed point

(see Problem 31.6). If we set all the functions on the RHS of Equation (31.23)

equal to zero,

we obtain

ω =0 and sinθ =0

corresponding to inﬁnitely many ﬁxed points at (nπ, 0) with n an integer.

Points in the neighborhood of the origin, i.e., those lying in the basin of

–3 -2 -1 0 1 2 3

–1.5

-1

–0.5

0.5

1.5

Figure 31.9: Phase space diagrams for a dissipative pendulum. Two trajectories

starting at θ ≈−π, ω =0and θ ≈ π, ω =0eventually end up at the origin.

Still assuming no driving force.

770 Nonlinear Dynamics and Chaos

attraction of the origin are attracted to the origin; the rest of the ﬁxed points

are repellors (or unstable) for such points.

The interesting motion of a pendulum begins when we turn on a driving

force regardless of whether the dissipative eﬀect is present or not. Neverthe-

less, let us place the pendulum in an environment in which γ =0.3. Now

drive this pendulum with a (harmonic) force of amplitude φ

=0.5 and angu-

lar frequency ω

= 1. A numerical solution of (31.23) will then give a result

which has a transient motion lasting until t ≈ 32. From t =32onward,the

system traverses a closed orbit in the phase diagram as shown in Figure 31.10.

This orbit is an attractor in the same sense as a point is an attractor for the

logistic map and a dissipative nondriven pendulum. An attractor such as the

one exhibited in Figure 31.10 is called a limit cycle.

limit cycle

31.2.3 Onset of Chaos

As we increase the control parameter φ

, the phase space trajectories go

through a series of periodic limit cycles until they ﬁnally become completely

aperiodic: chaos sets in. Figure 31.11 shows four trajectories whose common

initial angular displacement θ

, initial angular velocity ω

, damping factor γ,

and drive frequency ω

are, respectively, π,0,0.5,and2/3. The only (con-

trol) parameter that is changing is the amplitude of the driving force φ

.This

changes from 0.97 for the upper left to 1.2 for the lower right diagram.

A closer scrutiny of Figure 31.11—which we shall forego—will reveal that

the chaotic behavior of the diagram at the lower right takes place after the

pendulum goes through a bifurcation process as in the case of the logistic

map. However, unlike the logistic map whose bifurcation stages were divided

by ﬁxed “points,” the stages for the pendulum are characterized by limit cy-

cles. In fact, the diagram at the upper left, corresponding to φ

=0.97,

consists of two (very closely spaced) limit cycles. Bifurcations involving limit

cycles are called Hopf bifurcation after the mathematician E. Hopf who

Hopf bifurcation

generalized the earlier results of Poincar´e on such bifurcations to higher di-

mensions. The logistic map and the nonlinear pendulum have the following

property in common: their “route to chaos” is via bifurcation. This is not

4 5 6 7

–1.5

–1

–0.5

0.5

1.5

Figure 31.10: The moderately driven dissipative pendulum with γ =0.3 and φ

=0.5.

After a transient motion, the pendulum settles down into a closed trajectory.

31.2 Systems Obeying DEs 771

Figure 31.11: Four trajectories in the phase space of the damped driven pendulum.

The only diﬀerence in the plots is the value of φ

which is 0.97 for the upper left, 1.1

for the upper right, 1.15 forthelowerleft,and1.2 for the lower right diagrams.

true for all chaotic systems; there are other “routes to chaos,” but we shall

not investigate them here.

The main characteristic of chaos is the exponential divergence of neigh-

boring trajectories. We have seen this behavior for the logistic map. A very

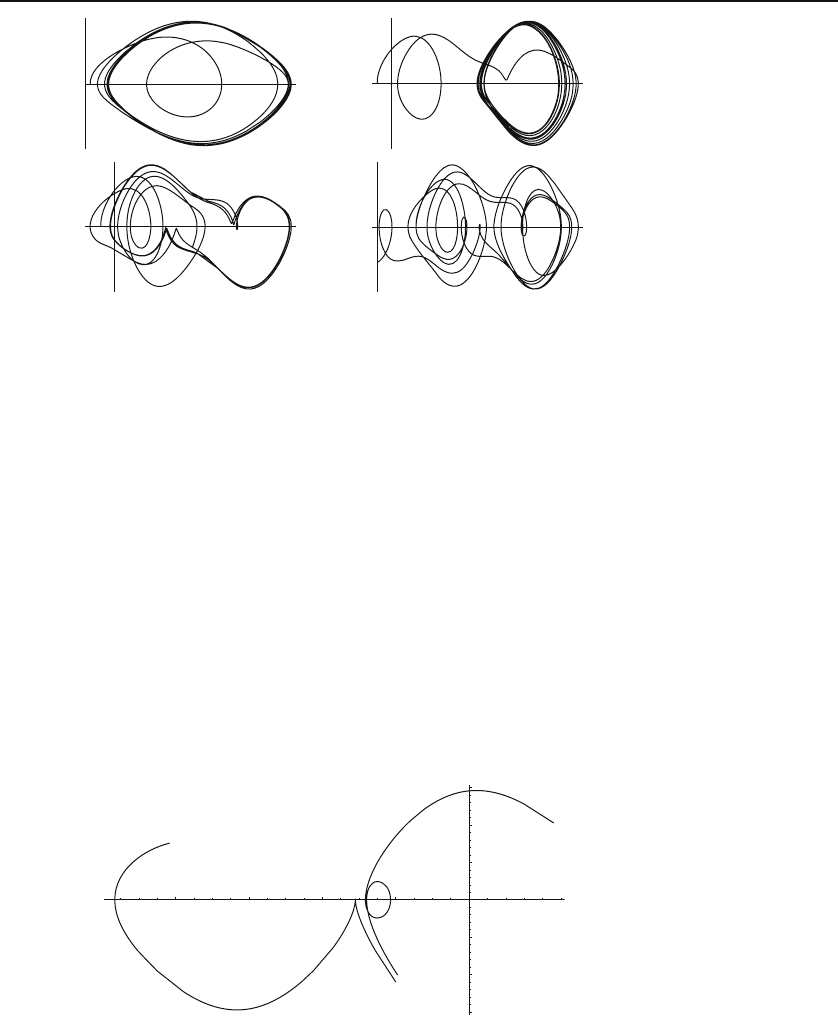
nice illustration of this phenomenon for the nonlinear pendulum is depicted

in Figure 31.12 where two nearby trajectories in the neighborhood of point

(−2, −2) are seen to diverge dramatically (in eight units of time).

The divergence of trajectories and the ensuing chaos has been termed the

butterﬂy eﬀect by Lorenz who, in the title of one of his talks, asked the

butterﬂy eﬀect

question: “Does the ﬂap of a butterﬂy’s wings in Brazil set oﬀ a tornado

in Texas?” The point Lorenz is making in this statement is that if the at-

mosphere displays chaotic behavior (as a simple model proposed by Lorenz

predicts), then a very small disturbance, such as the ﬂapping of a butterﬂy’s

–8 –6 –4 –2

–3

–2

–1

Figure 31.12: The projection onto the θω-plane of two trajectories starting at approxi-

mately the same point near (−2, −2) diverge considerably after eight units of time. The

loop does not contradict the DE uniqueness theorem!