Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

30.1 Variational Problem 731
the derivatives in (30.9) and solve the resulting differential equation. We
should emphasize that a path could be written as y(x) or any other form,
depending on the variables used in a particular problem.
Example 30.1.2.
Shortest Length Example 30.1.1 looked at very specific
paths connecting two points and found that the straight-line path minimizes the
length. Is this true for all paths?
For any path y(x), the length between (a, y
a
)and(b, y
b
) is given by the (30.3),
where the independent variable is x and dependent variable is y.Thus,L =
1+y
2
and the Euler-Lagrange equation becomes
∂L
∂y
−
d
dx
∂L
∂y
=0 or
d
dx
y
1+y
2
=0. (30.10)
Differentiating the expression inside the parentheses yields
y
(1 + y
2
)
3/2
=0, or y
=0, or y = cx + d,
where c and d are the constants of integration. This is the equation of a straight line.
Thus out of all the possible paths between (a, y
a
)and(b, y
b
), the straight line gives
the smallest length. Actually, we don’t know if the straight line is the shortest or the
longest distance. Euler-Lagrange equation, being the first derivative, is necessary,
but not sufficient. As in calculus, to show minimality one has to look at the second
derivatives. We shall do this later.
30.1.2 Beltrami identity
Most variational problems have an L which is independent of t. Insucha
case, the Euler-Lagrange equation simplifies considerably. Consider the total
derivative of L with respect to t:
dL
dt
=
∂L
∂x
˙x +
∂L
∂ ˙x
d ˙x
dt
.
Substitute for ∂L/∂x from Euler-Lagrange equation to obtain
dL
dt
=˙x
d
dt
∂L
∂ ˙x
+
∂L
∂ ˙x
d ˙x
dt
=
d
dt
˙x
∂L
∂ ˙x
, or
d
dt
L − ˙x
∂L
∂ ˙x
=0.
This gives the Beltrami identity:
L − ˙x
∂L
∂ ˙x
= C. (30.11)
Example 30.1.3.
The Brachistochrone Problem A bead slides on friction-
less bars of various shapes due to gravity. What shape gives the shortest time?
This is the famous brachistochrone problem which started the calculus of variations.
Specifically, consider various paths connecting P
a
=(x
a
,y
a
)andP
b
=(x
b
,y
b
)with
y
b
<y
a
.Amassm starts from rest at P
a
and moves on a frictionless path from P
a
to P
b
. Find the equation of the path that yields the shortest time.
732 Calculus of Variations
For each element ds of the path, the time of travel is dt = ds/v,wherev is the
speed at ds.Ifds is located at height y above the ground, then conservation of
energy gives
mgy
a
=
1
2
mv
2
+ mgy or v =
2g(y
a
− y).
Therefore,
L[y]=
#
P
b
P
a
ds
v
=
#
P
b
P
a
dx
2
+ dy
2
2g(y
a
− y)
=
#
x
b
x
a
"
1+y
2
2g(y
a
− y)
dx,
and L(y,y
)=
(1 + y
2
)/[2g(y
a
− y)]. Since L is independent of x, we can use the
Beltrami identity:
"
1+y
2
2g(y
a
− y)
− y
∂
∂y
"
1+y
2
2g(y
a
− y)
= C, or
1+y
2
− y
∂
∂y
1+y
2
= C
2g(y
a
− y).
Differentiating and simplifying the left-hand side gives
1
1+y
2
= C
2g(y
a
− y).
Square both sides, introduce a new constant, and solve for y
to get
dy
dx
=
"
k
y
a
− y
− 1.
The substitution u = k/(y
a
− y)givedy =(k/u
2
)du and changes the differential
equation to
k
u
2
du
dx
=
√
u − 1or
du
u
2
√
u − 1
=
1
k
dx.
Integrating both sides—and using an integral table—yields
x
k
=
√
u − 1
u
+tan
−1
√
u − 1
!
+ C.
As y → y
a
, u →∞and x → x
a
. Therefore, C = x
a
/k − π/2, and the solution
becomes
x − x
a
k
=
√
u − 1
u
+tan
−1
√
u − 1
!
−
π
2
. (30.12)
Let tan
−1
√
u − 1
!
= ϕ.Then
√
u − 1=tanϕ and
u =1+tan
2
ϕ =sec
2
ϕ or y = y
a
− k cos
2
ϕ. (30.13)
Substituting u in terms of ϕ in (30.12) yields
x − x
a
k
=sinϕ cos ϕ + ϕ −
π
2
.
Finally defining θ =2ϕ − π, this equation and (30.13) give x and y in terms of the
parameter θ:
x − x
a
=
k
2
(θ −sin θ) ,y− y
a
= −
k
2
(1 − cos θ) .
This is the parametric equation of a cycloid.
30.1 Variational Problem 733
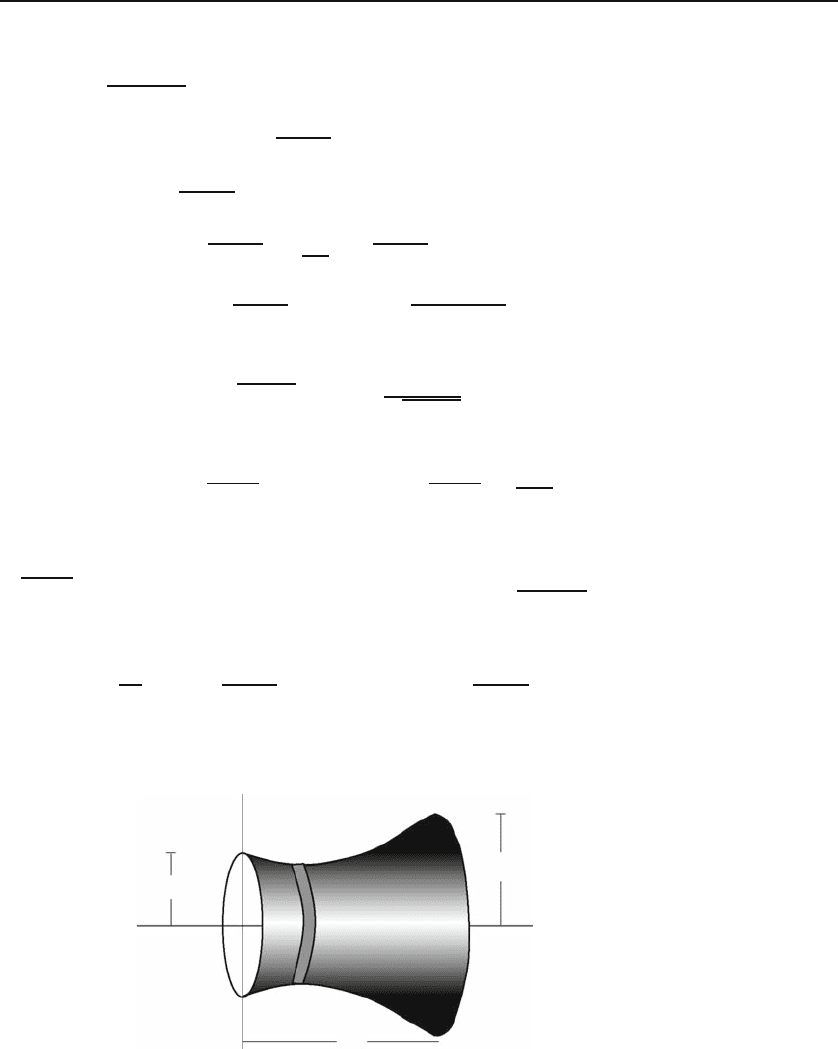
Example 30.1.4. The Soap Film Problem When a film of soap is stretched
across a frame, the surface tension causestheareatobeaminimum. Thefilmof
Figure 30.3 is an area of revolution with an element of area shown. This element of
area is 2πy
dx
2
+ dy
2
. Therefore, we have to extremize the functional
L[y]=2π
#
h
0
y
1+y
2
dx, y(0) = a, y(h)=b.
Since L(x, y, y
)=y
1+y
2
is independent of x,wecanusetheBeltramiidentity
and get
y
1+y
2
− y
∂
∂y
y
1+y
2
= C
1
.
This yields
y = C
1
1+y
2
or y
=
(y/C
1
)
2
− 1.
Let u = y/C
1
to simplify this equation to
C
1
u
=
(u
2
− 1orC
1
du
(u
2
− 1
= dx,
which can be easily integrated to give
x = C
1
ln
u +
u
2
− 1
+ C
2
or u +
u
2
− 1=e
x−C
2
C
1
≡ e
v
,
where v is the exponent of the exponential. From this, we get
u
2
− 1=e
v
− u or u
2
− 1=e
2v
− 2ue
v
+ u
2
or u =
e
v
+ e
−v
2
=coshv.
Returning to y and x,weobtain
y
C
1
=cosh
x − C
2
C
1
or y = C
1
cosh
x − C
2
C
1
.
The constants C
1
and C
2
can be found by the conditions y(0) = a, y(h)=b.
y
x
b
a
h
Figure 30.3: The soap film attaches itself to the two rings in such a way that the area
obtained is minimum.

734 Calculus of Variations
30.1.3 Several Dependent Variables
The path of (30.2) had only one dependent variable. One can consider paths in
an m-dimensional space where L depends on
,
x
α
(t)
-
m
α=1
and their derivatives.
Such a generalization is straightforward: In (30.4) instead of x(τ), we have
x
α
(τ), which changes (30.5) to
δ
δx
α
(τ)
L
x(t),
˙
x(t)
!
=
m
β=1
∂L
∂x
β
δx
β
(t)
δx
α
(τ)
+
∂L
∂ ˙x
β
δ ˙x
β
(t)
δx
α
(τ)
,
where x =(x
1
,x
2
,...,x
m
). For this we need the equivalent of (30.6) and
(30.7) which are easily shown to be
δx
β
(t)
δx
α
(τ)
= δ
αβ
δ(t − τ),
δ ˙x
β
(t)
δx
α
(τ)
= δ
αβ
d
dt
δ(t −τ). (30.14)
Substituting this in the above sum yields
δ
δx
α
(τ)
L
x(t),
˙
x(t)
!
=
∂L
∂x
α
δ(t −τ)+
∂L
∂ ˙x
α
d
dt
δ(t −τ),
which replaces the x and ˙x of (30.8) with x
α
and ˙x
α
. We thus obtain the
multivariable version of the Euler-Lagrange equation:
∂L
∂x
α
−
d
dt
∂L
∂ ˙x
α
=0,α=1, 2,...,m. (30.15)
30.1.4 Several Independent Variables
Equation (30.15) is one generalization of the Euler-Lagrange equation. It still
corresponds to a path, a (generally) curved line, albeit in a multi-dimensional
space. There is another generalization which is also important: going from a
path to a surface. In this case, our dependent variable is a function of several
independent variables. So, consider a function φ of m variables which we
collectively denote by x, and instead of (30.2) consider the functional
L[φ]=
##
Ω
d
m
xL(φ; φ
,1
,φ
,2
,...,φ
,m
; x), (30.16)
where φ
,α
denotes the derivative of φ with respect to x
α
,andΩissomeregion
in the m-dimensional space. Note the change in notation: we use L instead
of L when integration is over a multidimensional “volume.” The variational
derivative (30.5) now becomes
δ
δφ(y)
L
φ; φ
,1
,φ
,2
,...,φ
,m
; x
!
=
∂L
∂φ
δφ(x)
δφ(y)
+
m
α=1
∂L
∂φ
,α
δφ
,α
δφ(y)
. (30.17)
30.1 Variational Problem 735
Furthermore, (30.6) and (30.7) generalize to More fundamental
functional
derivatives
δφ(x)
δφ(y)
= δ(x − y),
δφ
,α
(x)
δφ(y)
=
∂
∂x
α
δ(x −y). (30.18)
Substituting these in the functional derivative of the integral (30.16) and
setting the result equal to zero yields another Euler-Lagrange equation:
∂L
∂φ
−
m
α=1
∂
∂x
α
∂L
∂φ
,α
=0. (30.19)
Finally if we have several dependent variables
,
φ
i
-
N
i=1
, collectively repre-
sented by Φ, and several independent variables {x
α
}
m
α=1
, collectively repre-
sented by x, then the variational functional becomes
L[Φ]=
##
Ω
d
m
xL(Φ; Φ
,1
, Φ
,2
,...,Φ
,m
; x), (30.20)
with the variational derivatives
δ
δφ
i
(y)
L
Φ; Φ
,1
, Φ
,2
,...,Φ
,m
; x
!
=
N
j=1
∂L
∂φ
j
δφ
j
(x)
δφ
i
(y)
+
N
j=1
m
α=1
∂L
∂φ
j
,α
δφ
j
,α
δφ
i
(y)
,
(30.21)
and
... and more
fundamental
functional
derivatives
δφ
j
(x)
δφ
i
(y)
= δ
ij
δ(x −y),
δφ
j
,α
(x)
δφ
i
(y)
= δ
ij
∂
∂x
α
δ(x −y). (30.22)
Substitution of these in (30.20) leads to the Euler-Lagrange equations
∂L
∂φ
i
−
m
α=1
∂
∂x
α
∂L
∂φ
i
,α
=0,i=1, 2,...,N. (30.23)
In many situations, the variational problem consists of various parts each
having one or several dependent or independent variables.
30.1.5 Second Variation
Euler-Lagrange equation was obtained by setting the first variational deriva-
tive (30.8) equal to zero. As in the multivariable calculus, this only finds
the extremum. And just as in the multivariable calculus, to see if we have a
minimum or a maximum, we have to run the second derivative test.
The easiest way to apply the second derivative test in calculus is to consider
the Taylor expansion of the function. And since we are interested in local
minima and maxima, we ignore the third and higher orders in the Taylor
expansion. Now recall from Section 10.7 that the Taylor series of a function

736 Calculus of Variations
f of N independent variables
,
x
i
-
N
i=1
≡ x up to the second order around x
0
is
f(x)=f(x
0
)+
N
i=1
(x
i
−x
0i
)f
,i
(x
0
)+
1
2
N
i,j=1
(x
i
−x
0i
)(x
j
−x
0j
)f
,ij
(x
0
), (30.24)
where
f
,i
≡
∂f
∂x
i
and f
,ij
≡
∂
2
f
∂x
i
∂x
j
.
If x
0
is an extremum of f,thenf
,i
(x
0
) = 0 and the above equation becomes
f(x) − f(x
0
)=
1
2
N
i,j=1
(x
i
− x
0i
)(x
j
− x
0j
)f
,ij
(x
0
) ≡ δ
2
f(x
0
), (30.25)
where we introduced the abbreviation δ
2
f(x
0
)—the second variation of f at
x
0
—for the sum. The test for maximum or minimum of f can now be stated:
If for any x that is close enough to x
0
, the second variation δ
2
f(x
0
) is positive,
then x
0
is a minimum point, and if δ
2
f(x
0
) is negative, then x
0
is a maximum
point.
The generalization to the variational problem follows from our usual pas-
sage from the discrete to the continuous. For the most general integral (30.20),
the second variation is
δ
2
L[Φ
0
]=
1
2
N
i,j=1
##
Ω
d
m
x
##
Ω
d
m
y
φ
i
(x) −φ
i
0
(x)
φ
i
(y) − φ
i
0
(y)
δ
2
L
δφ
i
(x)δφ
j
(y)
[Φ
0
], (30.26)
where the last term means “find the second variational derivative and evaluate
the result at the solution Φ
0
of the Euler-Lagrange equation.” For a single
dependent variable and several independent variables this becomes
δ
2
L[φ
0
]=
1
2
##
Ω
d
m
x
##
Ω
d
m
y
φ(x) − φ
0
(x)
φ(y) − φ
0
(y)
δ
2
L
δφ(x)δφ(y)
[φ
0
],
(30.27)
and for a single independent variable and several dependent variables we get
δ
2
L[x
0
]=
1
2
N
i,j=1
#
b
a
dt
#
b
a
dτ
x
i
(t)−x
i0
(t)
x
j
(τ)−x
j0
(τ)
δ
2
L
δx
i
(t)δx
j
(τ)
[x
0
],
(30.28)
and for the simplest case of a single independent variable and a single depen-
dent variable (30.26) reduces to
δ
2
L[x
0
]=
1
2
#
b
a
dt
#
b
a
dτ
x(t)−x
0
(t)
x(τ)−x
0
(τ)
δ
2
L
δx(t)δx(τ)
[x
0
]. (30.29)
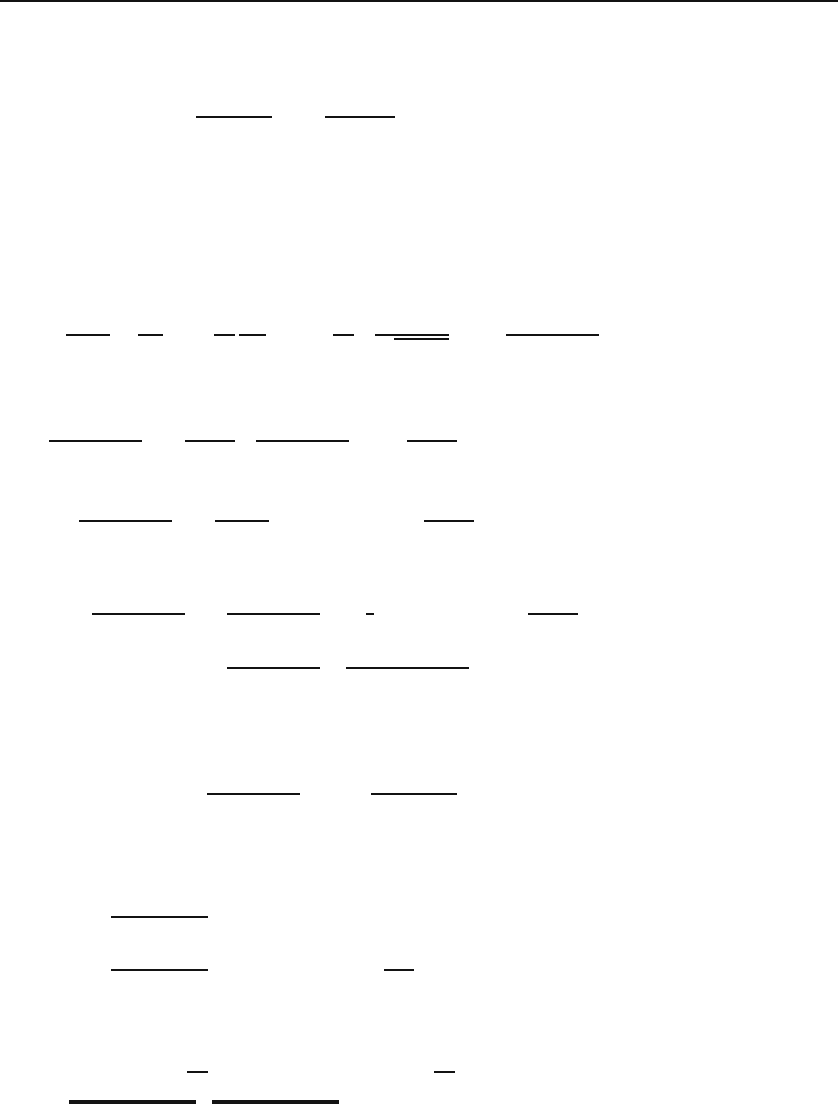
30.1 Variational Problem 737
In the calculation of the second variation, we need to find the variational
derivatives of second derivatives of dependent variables. It is not hard to show
that
Fundamental
functional
derivatives
involving second
partial derivatives
δφ
j
,αβ
(x)
δφ
i
(y)
= δ
ij
∂
2
∂x
β
∂x
α
δ(x −y). (30.30)
Example 30.1.5.
The necessary condition for the straight line to be the shortest
distance between two given points is that it satisfies the Euler-Lagrange equation
(30.10). Example 30.1.2 showed that y
0
(x)=cx+d solves the Euler-Lagrange equa-
tion. To see if this is minimum or not, calculate the second variation (30.29). The
first derivative is given by (30.8), which with the current symbols for independent
and dependent variables, becomes
δL[y]
δy(x)
=
∂L
∂y
(x) −
d
dx
∂L
∂y
(x)=−
d
dx
y
1+y
2
= −
y
(1 + y
2
)
3/2
,
and
δ
2
L[y]
δy(x
)δy(x)
= −
δ
δy(x
)
0
y
(1 + y
2
)
3/2
1
= −
δ
δy(x
)
3
y
1+y
2
!
−3/2
4
,
or
δ
2
L[y]
δy(x
)δy(x)
= −
δy
(x)
δy(x
)
1+y
2
!
−3/2
− y
δ
δy(x
)
1+y
2
!
−3/2
.
Using (30.30), this yields
δ
2
L[y]
δy(x
)δy(x)
= −
δ
(x − x
)
(1 + y
2
)
3/2
+ y
3
2
(2y
)
1+y
2
!
−5/2
δy
(x)
δy(x
)
= −
δ
(x − x
)
(1 + y
2
)
3/2
+
3y
y
δ
(x − x
)
(1 + y
2
)
5/2
.
Nowwehavetoevaluatethisatthesolutiony
0
(x) of the Euler-Lagrange equation
for which y
0
= c and y
0
=0. Thus,
δ
2
L[y]
δy(x
)δy(x)
[y
0
]=−
δ
(x − x
)
(1 + c
2
)
3/2
.
Substituting this in (30.29) and using the derivative property (5.12) of the Dirac
delta function yields
δ
2
L[y
0
]=−
1
2(1 + c
2
)
3/2
#
b
a
dx
#
b
a
dx
y(x) − y
0
(x)
y(x
) − y
0
(x
)
δ
(x − x
)
= −
1
2(1 + c
2
)
3/2
#
b
a
dx
y(x) − y
0
(x)
d
2
dx
2
y(x) − y
0
(x)
.
The last integral can be integrated by parts to give
y(x) − y
0
(x)
d
dx
y(x) − y
0
(x)
b
a
=0 because y(a)=y
0
(a), y(b)=y
0
(b)
−
#
b
a
dx
(
d
dx
y(x) − y
0
(x)
)
2
.

738 Calculus of Variations
Therefore,
δ
2
L[y
0
]=
1
2(1 + c
2
)
3/2
#
b
a
dx
(
d
dx
y(x) − y
0
(x)
)
2
,
which is a manifestly positive quantity for any y(x). Hence, y
0
(x)=cx + d does
indeed minimize the distance between any two given points.
We should emphasize that although the calculation of the second varia-
tional derivative is rather straightforward, showing that the second variation
δ
2
L—the integral of the second variational derivative as given in Equations
(30.26) to (30.29)—is positive or negative is by no means trivial. Example
30.1.5 is one of those rare cases where the calculation of δ
2
L is manageable.
30.1.6 Variational Problems with Constraints
The variational problems treated so far have been problems with boundary
conditions, namely that all “paths,” or extremal candidates, must go through
the same boundary. In many applications, there are other auxiliary conditions
or constraints that the extremal candidates must obey. A typical example is
the problem of finding the closed curve of the largest area when the perimeter
is a given fixed length. The most elegant way of treating the constrained
variational problems is via Lagrange multipliers discussed in Section 12.3.1.
Suppose that we are looking for a curve that not only extremizes L[x]of
Isoperimetric
problem
(30.2), but also is such that another functional,
K[x]=
#
b
a
G
x(t), ˙x(t),t
!
dt, (30.31)
takes a fixed value l. Such a problem is called isoperimetric.Inexact
analogy with the multivariable calculus, we form a new function L + λG and
extremize that function. This means that we have to solve the Euler-Lagrange
equation
∂L
∂x
−
d
dt
∂L
∂ ˙x
+ λ
∂G
∂x
−
d
dt
∂G
∂ ˙x
=0. (30.32)
Example 30.1.6.
As an example of the isoperimetric variational problem, con-
sider all curves of length l in the upper half plane passing through the points (−a, 0)
and (a, 0). What is the equation of the curve that together with the interval [−a, a]
encloses the largest area? The sought-after function y(x)mustextremize
L[y]=
#
a
−a
ydx,
subject to the condition that
y(−a)=0=y(a), K[y]=
#
a
−a
1+y
2
dx = l.
Equation (30.32) with L = y and G =
1+y
2
gives
1+λ
d
dx
y
1+y
2
=0.
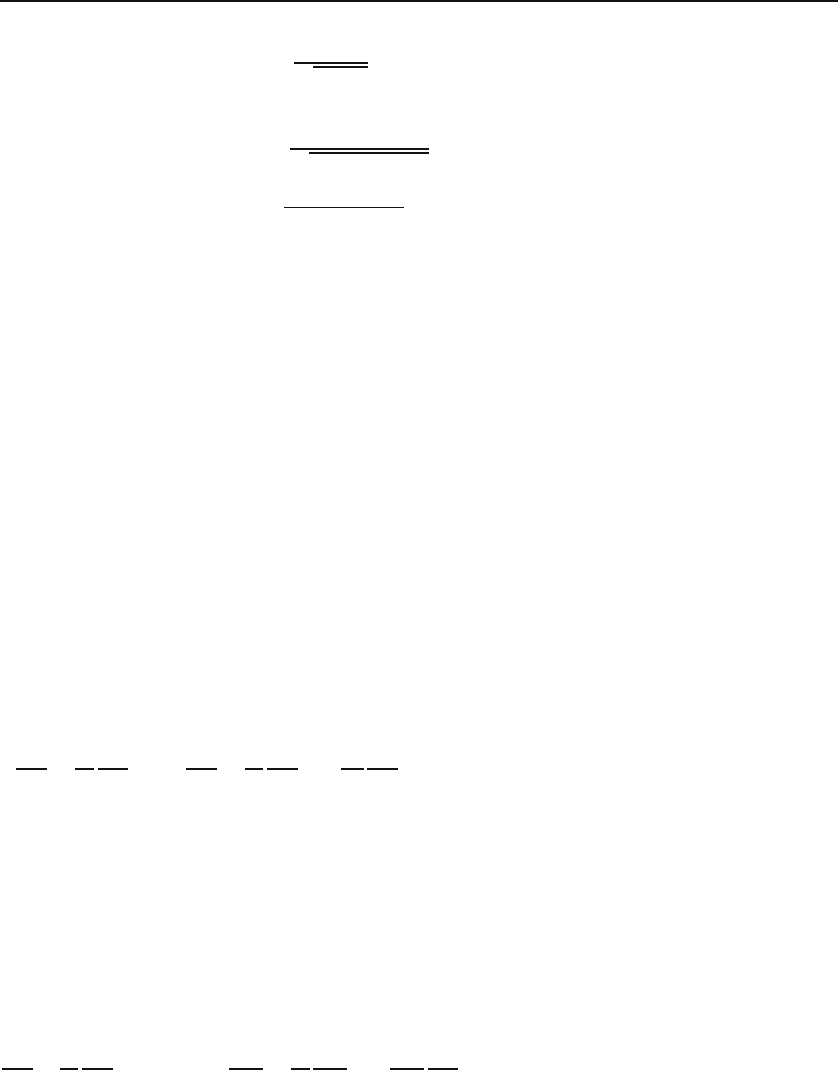
30.1 Variational Problem 739
Integrating this yields
x + λ
y
1+y
2
= C
1
,
which can be solved for y
to give
y
= ±
C
1
− x
λ
2
− (C
1
− x)
2
,
whose solution is
y = ±
λ
2
− (C
1
− x)
2
+ C
2
,
or
(x − C
1
)
2
+(y − C
2
)
2
= λ
2
.
This is a circle of radius λ. The values of the three unknowns C
1
, C
2
,andλ are
determined from the conditions
y(−a)=0=y(a), K[y]=l.
There is another type of variational problem with constraint applicable Finite constraint
problem
to the case of one independent and several dependent variables, in which the
constraint is given by an equation of the form
g
x(t),
˙
x(t),t
!
=0
This is called the finite constraint problem and is similar to Equation
(12.31) where the discrete index j has been replaced with the continuous index
t. Thus, the Lagrange multipliers λ
j
should be replaced with λ(t)andthe
sum in (12.32) replaced with an integral over t, which is already present in the
extremal problem. Therefore, the problem changes to finding the extremum
of
#
b
a
,
L
x(t),
˙
x(t),t
!
+ λ(t)g
x(t),
˙
x(t),t
!-
dt, (30.33)
and the Euler-Lagrange equation becomes
∂L
∂x
i
−
d
dt
∂L
∂ ˙x
i
+ λ
∂g
∂x
i
−
d
dt
∂g
∂ ˙x
i
−
dλ
dt
∂g
∂ ˙x
i
=0,i=1, 2,...,N. (30.34)
If there are multiple constraint equations,
g
α
x(t),
˙
x(t),t
!
=0,α=1, 2,...,m,
then there will be m Lagrange multipliers and a sum over α in (30.33),
#
b
a
0
L
x(t),
˙
x(t),t
!
+
m
α=1
λ
α
(t)g
α
x(t),
˙
x(t),t
!
1
dt, (30.35)
leading to the following Euler-Lagrange equation:
∂L
∂x
i
−
d
dt
∂L
∂ ˙x
i
+
m
α=1
(
λ
α
∂g
α
∂x
i
−
d
dt
∂g
α
∂ ˙x
i
−
dλ
α
dt
∂g
∂ ˙x
i
)
=0,i=1, 2,...,N.
(30.36)
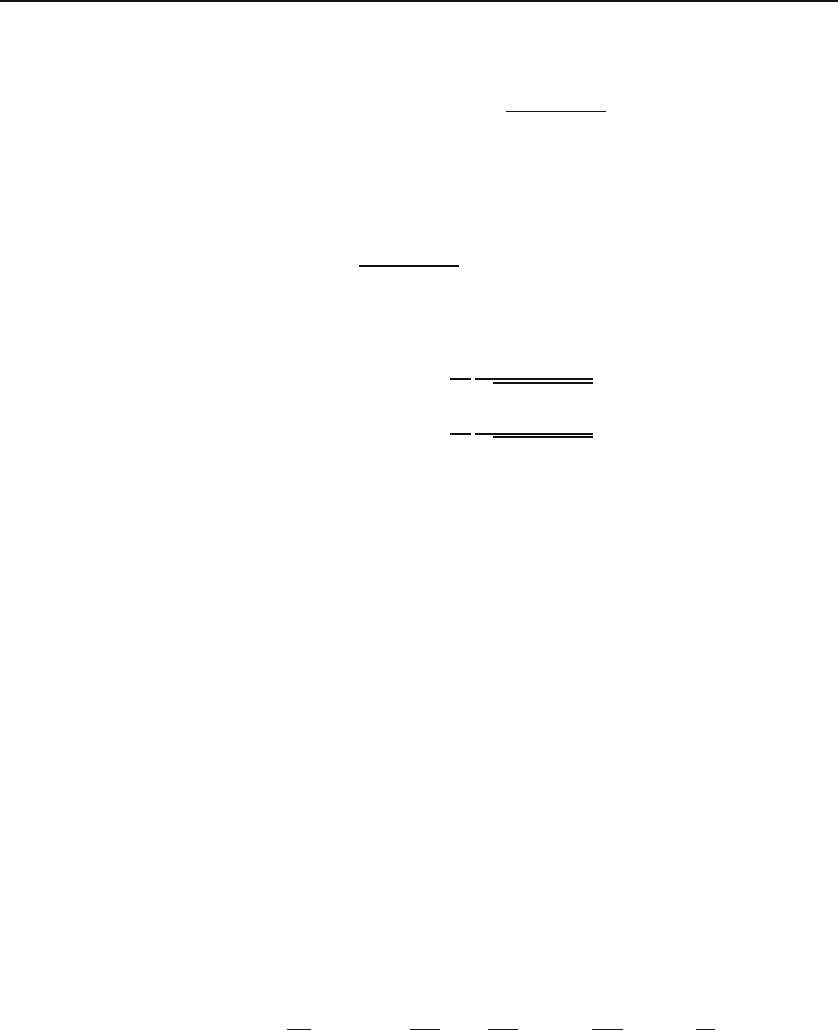
740 Calculus of Variations
Example 30.1.7. Among all curves lying on the sphere centered at the origin
and of radius a and passing through two points (x
1
,y
1
,z
1
)and(x
2
,y
2
,z
2
), find the
shortest one. This is a finite constraint problem with
L[y,z]=
#
x
2
x
1
1+y
2
+ z
2
dx
and
g(x, y, z)=x
2
+ y
2
+ z
2
− a
2
.
The solution is the set of functions {y(x),z(x)} which extremize the integral
#
x
2
x
1
3
1+y
2
+ z
2
+ λ(x)(x
2
+ y
2
+ z
2
− a
2
)
4
dx,
i.e., functions that satisfy the Euler-Lagrange equations
2yλ(x) −
d
dx
y
1+y
2
+ z
2
=0,
2zλ(x) −
d
dx
z
1+y
2
+ z
2
=0.
Solving these equations, we get the solutions in terms of four constants which can
be determined from the boundary conditions
y(x
1
)=y
1
,y(x
2
)=y
2
,
z(x
1
)=z
1
,z(x
2
)=z
2
.
30.2 Lagrangian Dynamics
Variational calculus has become an indispensable tool in physics. Almost all
(partial) differential equations of physics can be derived from some variational
problem. Furthermore, symmetry considerations, which are the cornerstones
of modern fundamental physics, find their natural settings in functionals.
And a very elegant and powerful formulation of quantum mechanics done by
Richard Feynman uses the variational techniques.
30.2.1 From Newton to Lagrange
For most conservative systems one can define functionals whose extremization
leads to differential equations of motion of those systems. The second law of
motion for a particle acted on by a conservative force can be written as
−∇Φ=m
dv
dt
or −
∂Φ
∂x
i
= m
d ˙x
i
dt
or
∂
∂x
i
(−Φ) −
d
dt
(m ˙x
i
)=0.
(30.37)
This looks very much like (30.15)! Let’s see if we can construct an L that leads
to the equations of mechanics. Use x, y,andz for the moment with n =3.
