Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

29.1 The Fourier Transform 701

If a charge distribution is involved, the inverse Fourier transform will be interestingly

diﬀerent as the following example shows.



Example 29.1.4. The example above deals with the electrostatic potential of a

point charge. Let us now consider the case where the charge is distributed over a

ﬁnite volume. Then the potential is

V (r)=

###

qρ(r



)



− r|



≡ k

ρ(r



)



− r|



where qρ(r



) is the charge density at r



, and we have used a single integral because



already indicates the number of integrations to be performed. Note that we

have normalized ρ(r



) so that its integral over the volume is 1. Figure 29.5 shows

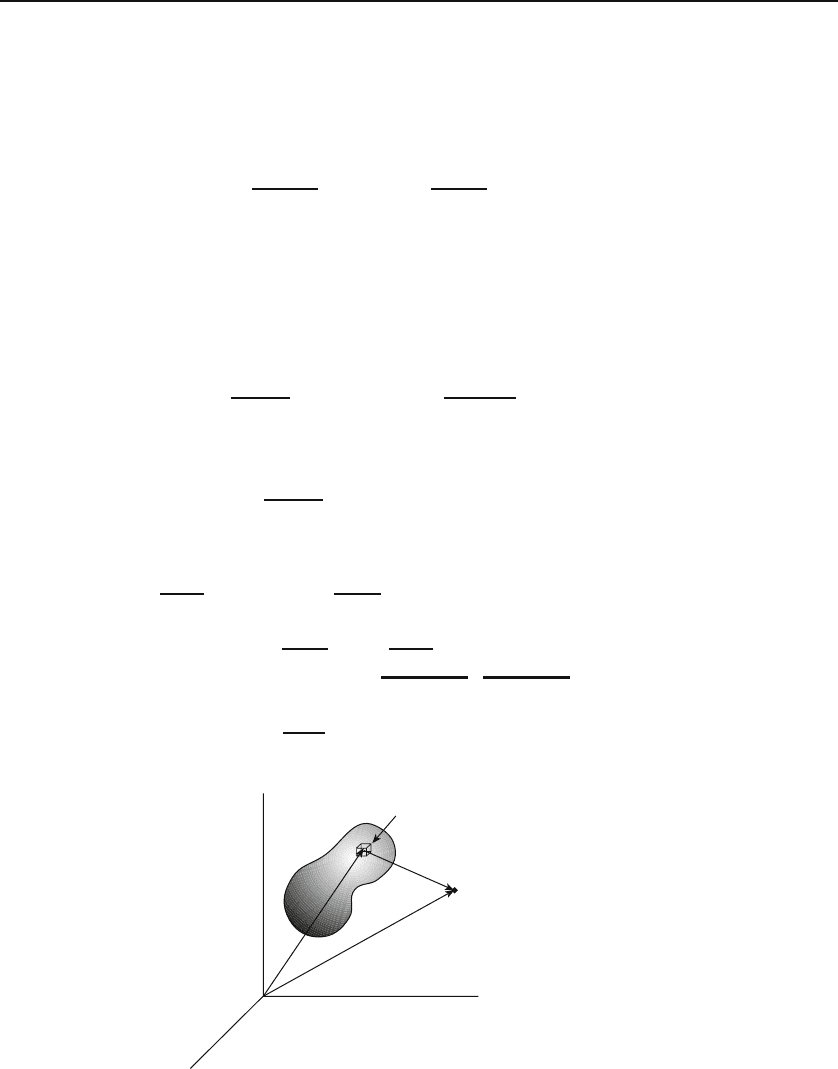
the geometry of the situation.

Making a change of variables, R ≡ r



− r,orr



= R + r,andd



= d

X,with

R ≡ (X, Y, Z), we get

−1

[V ](k) ≡

V (k)=

(2π)

3/2

−ik·r

ρ(R + r)

X. (29.13)

To evaluate Equation (29.13), we substitute for ρ(R + r) in terms of its Fourier

transform,

ρ(R + r)=

(2π)

3/2



˜ρ(k



·(R+r)

. (29.14)

Combining (29.13) and (29.14), we obtain

V (k)=

(2π)



·R

˜ρ(k



ir·(k



−k)

= k



·R

˜ρ(k



)



(2π)

ir·(k



−k)





 

δ(k



−k)by Equation (18.30)

= k

q ˜ρ(k)

ik·R

. (29.15)

′

−

′

Figure 29.5: The inverse Fourier transform of the potential of a continuous charge

distribution at P is calculated using this geometry.

702 Integral Transforms

What is nice about this result is that the contribution of the charge distribution,

˜ρ(k), has been completely factored out. The integral, aside from a constant and a

change in the sign of k, is simply the inverse Fourier transform of the Coulomb

potential of a point charge obtained in the previous example. We can therefore

write Equation (29.15) as

V (k)=(2π)

3/2

˜ρ(k)

Coul

(−k)=

4πk

q ˜ρ(k)

|k|

This equation is important in analyzing the structure of atomic particles. The

inverse Fourier transform

V (k) is directly measurable in scattering experiments.

In a typical experiment a (charged) target is probed with a charged point particle

(electron). If the analysis of the scattering data shows a deviation from 1/k

in the

behavior of

V (k), then it can be concluded that the target particle has a charge

distribution. More speciﬁcally, a plot of k

V (k)versusk gives the variation of

˜ρ(k), the form factor,withk. If the resulting graph is a constant, then ˜ρ(k)isaform factor

constant, and the target is a point particle [˜ρ(k) is a constant for point particles,

where ˜ρ(r



) ∝ δ(r − r



)]. If there is any deviation from a constant function, ˜ρ(k)

must have a dependence on k, and correspondingly, the target particle must have a

charge distribution.

The above discussion, when generalized to four-dimensional relativistic space-Fourier transform

and the discovery

of quarks

time, was the basis for a strong argument in favor of the existence of point-like

particles—quarks—inside a proton in 1968, when the results of the scattering of

high-energy electrons oﬀ protons at the Stanford Linear Accelerator Center revealed

deviation from a constant for the proton form factor.



29.1.4 Application to Diﬀerential Equations

The Fourier transform is very useful for solving diﬀerential equations. This is

because the derivative operator in r space turns into ordinary multiplication

in k space. For example, if we diﬀerentiate f (r) in Equation (29.10) with

respect to x

,weobtain

∂

∂x

f(r)=

(2π)

n/2

∞

∂

∂x

i(k

+···+k

)

f(k)

(2π)

n/2

∞

k(ik

ik·r

f(k). (29.16)

That is, every time we diﬀerentiate with respect to any component of r,the

corresponding component of k “comes down.” Thus, the n-dimensional gra-

dient and Laplacian can be written as

∇

∇f(r)=(2π)

−n/2

k(ik)e

ik·r

f(k)

∇

f(r)=(2π)

−n/2

k(−k

ik·r

f(k). (29.17)

29.1 The Fourier Transform 703

Let us illustrate the above points with a simple example. Consider the

ordinary second-order diﬀerential equation

+ C

x = f(t), (29.18)

where C

,andC

are constants. We can “solve” this equation by simply

substituting the following in it:

x(t)=

√

2π

∞

−∞

dω˜x(ω)e

iωt

√

2π

∞

−∞

dω˜x(ω)(iω)e

iωt

= −

√

2π

∞

−∞

dω˜x(ω)ω

iωt

,f(t)=

√

2π

∞

−∞

dω

f(ω)e

iωt

This gives

√

2π

∞

−∞

dω˜x(ω)(−C

+ iC

ω + C

iωt

√

2π

∞

−∞

dω

f(ω)e

iωt

Equating the coeﬃcients of e

iωt

on both sides, we obtain

˜x(ω)=

f(ω)

−C

+ iC

ω + C

. (29.19)

If we know

f(ω) [which can be obtained from f (t)], we can calculate x(t)

by Fourier-transforming ˜x(ω). The resulting integrals are not generally easy

to evaluate. In some cases the methods of complex analysis may be helpful; in

others numerical integration may be the last resort. However, the real power

of the Fourier transform lies in the formal analysis of diﬀerential equations.

Example 29.1.5.

A harmonically driven circuit consisting of an inductor L,a

resistor R, and a capacitor C, obeys the following diﬀerential equation:

+ R

= E cos ω

where Q is the charge on the capacitor. Except for the constants, this is identical

to (29.18). The Fourier transform of cosine is a sum of two Dirac delta functions

(see Problem 29.6). Substituting in Equation (29.19), we obtain

Q(ω)=E



δ(ω − ω

)+δ(ω + ω

)

−Lω

+ iRω +(1/C)

Therefore,

Q(t)=

√

2π

∞

−∞

dω

Q(ω)e

iωt

∞

−∞

dω

δ(ω − ω

)+δ(ω + ω

)

−Lω

+ iRω +(1/C)

iωt



iω

−Lω

+ iRω

+(1/C)

−iω

−Lω

− iRω

+(1/C)



704 Integral Transforms

Noting that the second term in the outer parentheses is the complex conjugate of

the ﬁrst term, we obtain

Q(t)=

2Re



iω

−Lω

+ iRω

+(1/C)



and using Re(z

∗

)=(x

)/|z

,wherex and y are the real and imaginary

parts of a complex number z, we ﬁnally obtain

Q(t)=E

[(1/C) − Lω

]cosω

t + Rω

sin ω

[−Lω

+(1/C)]

+ R

for the charge on the capacitor and

I(t)=

= E

−[(1/C) − Lω

]ω

sin ω

t + Rω

cos ω

[−Lω

+(1/C)]

+ R

for the current in the circuit. Note the occurrence of a resonance (large current)

at the voltage source frequency of ω

=1/

√

LC. Note also that the Q(t) obtained

above is a particular, not the most general, solution of the diﬀerential equation (see

Box 24.4.1).



Example 29.1.6. The one-dimensional heat equation, the PDE governing the

behavior of the temperature T (x, t)alongarod,is

∂T

∂t

= κ

∂

∂x

, (29.20)

wherewehaveusedκ [see Equation (22.3)] to leave k exclusively for Fourier trans-

forms. Write T (x, t) as a Fourier transform in the x variable

T (x, t)=

√

2π

∞

−∞

T (k, t)e

ikx

dk, (29.21)

and substitute in (29.20) to obtain

√

2π

∞

−∞

∂

∂t

ikx

dk =

√

2π

∞

−∞

(−κ

)

T (k, t)e

ikx

dk or

∂

∂t

= −κ

T (k, t)

This is a ﬁrst order ordinary diﬀerential equation which can be easily solved

T (k, t)=C(k)e

−κ

, (29.22)

where C(k) is the constant of integration, which could depend on k. Now suppose

that initially the temperature distribution on the rod is T (x, 0) = f(x), where f(x)

is a given known function. Then the last equation gives

T (k, 0) = C(k), and (29.21)

yields

f(x)=T (x, 0) =

√

2π

∞

−∞

T (k, 0)e

ikx

dk =

√

2π

∞

−∞

C(k)e

ikx

dk,

showing that C(k) is the inverse Fourier transform of f(x):

C(k)=

√

2π

∞

−∞

f(x)e

−ikx

dx.

29.2 Fourier Transform and Green’s Functions 705

Substituting this in (29.22) and the result in (29.21) yields

T (x, t)=

2π

∞

−∞



∞

−∞

f(y)e

−iky



−κ

ikx

2π

∞

−∞

f(y) dy

∞

−∞

−κ

t+ik(x−y)

dk. (29.23)

The inner integral can be done by completing the square in the exponent as in

Example 29.1.2. The result is

∞

−∞

−κ

t+ik(x−y)

dk =

√

−

(x−y)

4κ

√

Putting this in (29.23) and noting that f(y)=T (y,0), we ﬁnally obtain

T (x, t)=

√

4πκ

∞

−∞

T (y, 0)e

−

(x−y)

4κ

dy. (29.24)

If we know the initial shape of the temperature distribution T (y,0) on the rod,

we can calculate the temperature at every point of the rod for any time. A simple

example is if the temperature is inﬁnitely hot at one point, say x

of the rod and

zero every where else. Then

T (y,0) = T

δ(y − x

and (29.24) yields

T (x, t)=

√

4πκ

∞

−∞

δ(y − x

−

(x−y)

4κ

dy =

−

(x−x

)

4κ

√

4πκ



29.2 Fourier Transform and Green’s Functions

Suppose you are given a system of n linear equations in n unknowns and asked

to slove them. An elegant approach would be to use matrices. So, let L be

the matrix of coeﬃcients, y the column vector of the n unknowns, and f the

column vector of the constants appearing on the right-hand side of the system

of equations. The matrix equation and the corresponding system of equations

would look like the following:

Ly = f,



j=1

= f

,i=1, 2,...,n. (29.25)

If L has an inverse G, i.e., if there is a matrix G such that LG = 1,then

the solution to the above equation can formally be written as y = Gf,orin

component form as



j=1

,i=1, 2,...,n. (29.26)

706 Integral Transforms

Thus, the problem of solving the system of linear equations turns into the

problem of ﬁnding the inverse of the coeﬃcient matrix; and this is independent

of what f is!OnceIknowtheinverseofL,Icansolveany system of linear

equations, regardless of the constants on the right-hand side. Recalling that

the elements of the unit matrix are just the correctly labeled Kronecker delta,

the equation that G has to satisfy becomes

LG = 1,



j=1

= δ

,i,k=1, 2,...,n. (29.27)

Now think of a column vector v as a “machine:” feed the machine an

From discrete

matrices to

continuous

diﬀerential

operators

integer between 1 and n, and it will give you a real number, i.e., the element

of the column vector carrying the integer as an index. Similarly, think of a

matrix M as another “machine” which gives you a real number if you feed it

a pair of integers between 1 and n. Write this as

v(i)=v

, and M(i, j)=M

,i,j=1, 2,...,n. (29.28)

Would it be beneﬁcial to generalize the action of the machine to include

all real numbers? A vector machine that feeds on real numbers is a function:

feed a function a real number and it will spit out a real number. Replacing

i with x,wehavev(x)=v

≡ v(x), because v

is not a common notation.

Similarly, M(x, x



)=M



≡ M (x, x



). Furthermore, all summations have

to be replaced by integrals. For example, the system of equations (29.25)

becomes

Ly = f

L(x, x



)y(x



) dx



= f(x),

where (a, b) is a convenient interval of the real line usually taken to be

(−∞, ∞). What is the meaning of L(x, x



)? It can be merely a function

of two variables. But more interestingly, it can be a diﬀerential operator.

However, a diﬀerential operator is a local operator, i.e., it is a linear combi-

nation of derivatives of various orders at a single point,sayx. This requires

the last integral above to collapse to x. The only way that can happen is if

L(x, x



)=δ(x − x



)L(x) ≡ δ(x −x



, (29.29)

where L

is by deﬁnition a diﬀerential operator in the variable x.

Now that we have a diﬀerential operator which is the generalization of a

matrix, how do we ﬁnd its inverse? In other words, how do we generalize

Equation (29.27)? We suspect that the Kronecker delta turns into a Dirac

delta function. With this suspicion, we generalize (29.27) to

LG = 1,

L(x, x



)G(x



)=δ(x −x

Substituting (29.29) in the second equation yields

Diﬀerential

equation for

Green’s function

δ(x −x



G(x



)=δ(x − x

29.2 Fourier Transform and Green’s Functions 707

G(x, x

)=δ(x −x

). (29.30)

A function which satisﬁes this equation is called the Green’s function for

the diﬀerential operator L

. If we can ﬁnd the Green’s function for L

,then

the solution to the diﬀerential equation L

y(x)=f(x) can be written as the

generalization of (29.26):

y(x)=

G(x, x



)f(x



) dx



. (29.31)

To show this, note that

y(x)=L

G(x, x



)f(x



) dx



G(x, x



)f(x



) dx



δ(x −x



)f(x



) dx



= f(x).

Green’s functions are powerful tools for solving diﬀerential equations. Or-

dinary diﬀerential equations have ordinary derivatives and the diﬀerential

operator involves a single variable. Partial diﬀerential equations correspond

to diﬀerential operators involving several variables. If x denotes the collec-

tion of all these variables, then the diﬀerential operator can be denoted by L

and the Green’s function by G(x, x



), which satisﬁes the partial diﬀerential

equation

G(x, x



)=δ(x −x



). (29.32)

Since Fourier transform turns diﬀerentiation into multiplication, and the

Dirac delta function has a very simple inverse Fourier transform, Green’s

function are very elegantly calculated via Fourier transform techniques. For

example, if L

is a second order partial diﬀerential operator with constant

coeﬃcients in n variables, then Fourier transforming only the x variables and

writing

G(x, x



(2π)

n/2

G(k, x



ik·x

δ(x −x



(2π)

ik·(x−x



)

, (29.33)

the diﬀerential equation (29.32) becomes

G(k, x



ik·x

(2π)

n/2

ik·(x−x



)

(2π)

n/2

ik·x

−ik·x



When L

acts on the exponential, it produces a polynomial p(k

) of second Green’s function

in n dimensions

degree in components k

of k. Therefore, equating the coeﬃcient of e

ik·x

both sides, we obtain

G(k, x



)p(k

(2π)

n/2

−ik·x



G(k, x



(2π)

n/2

−ik·x



p(k

)

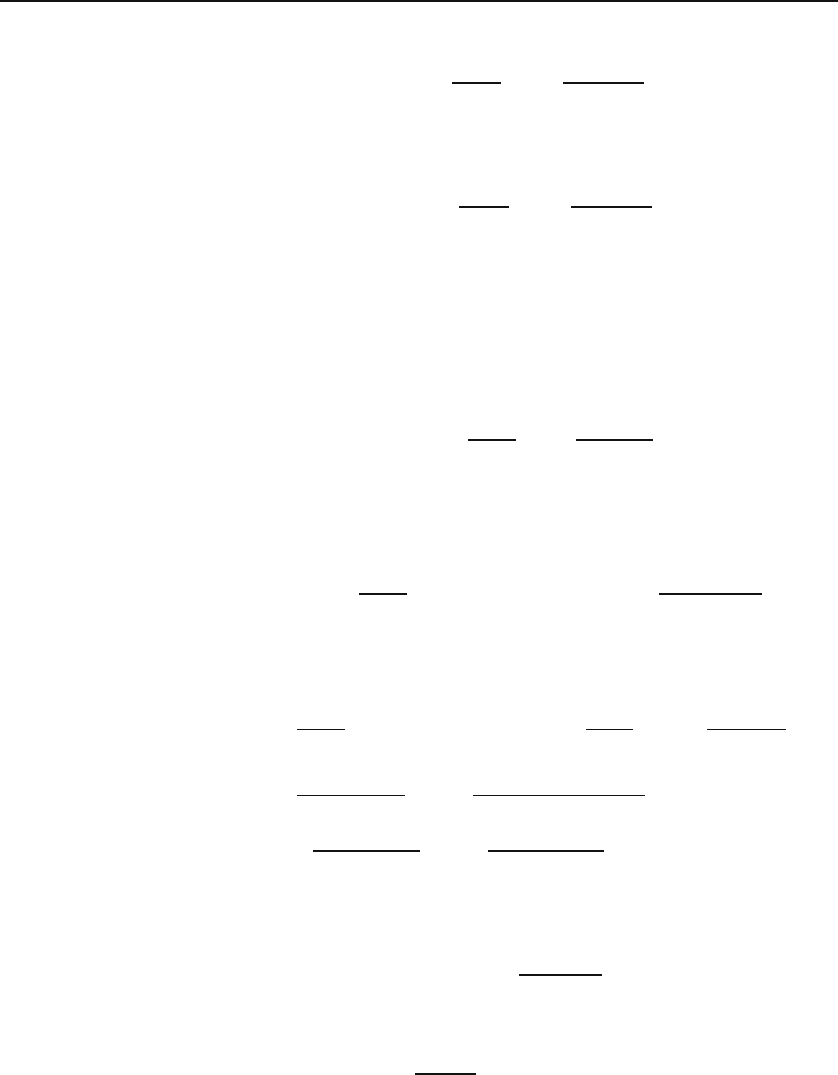
708 Integral Transforms

Substituting this in the ﬁrst equation of (29.33), we get

G(x, x



(2π)

ik·(x−x



)

p(k

)

which shows that the Green’s function is a function of the diﬀerence between

its arguments. We therefore have

G(x − x



(2π)

ik·(x−x



)

p(k

)

. (29.34)

29.2.1 Green’s Function for the Laplacian

Equation (29.17) tells us that p(k

)=−k

for the Laplacian. Thus, with

n = 3, (29.34) becomes

G(r −r



)=−

(2π)

ik·(r−r



)

. (29.35)

To evaluate this integral, use spherical coordinates in the k-space, and choose

the polar axis to be along the vector r − r



. Then, d

k = k

sin θdkdθdϕ and

(29.35) becomes

G(r −r



)=−

(2π)

∞

sin θdθ

2π

dϕ

ik|r−r



|cos θ

The ϕ integration gives 2π.Fortheθ integration, let u =cosθ. Then the

integral becomes

G(r − r



(2π)

∞

−1

due

ik|r−r



(2π)

∞

ik|r−r



ik|r − r





−1

(2π)

|r − r



∞

−ik|r−r



− e

ik|r−r



= −

(2π)

|r − r



∞

sin (k|r −r



Example 21.3.3 calculated the last integral and yielded π/2forit. Wethus

obtain the important result that for the Laplacian, the Green’s function is

G(r − r



)=−

4π|r − r



. (29.36)

From this and ∇

G(r − r



)=δ(r − r



), we obtain another important result:

∇



|r − r





= −4πδ(r −r



). (29.37)

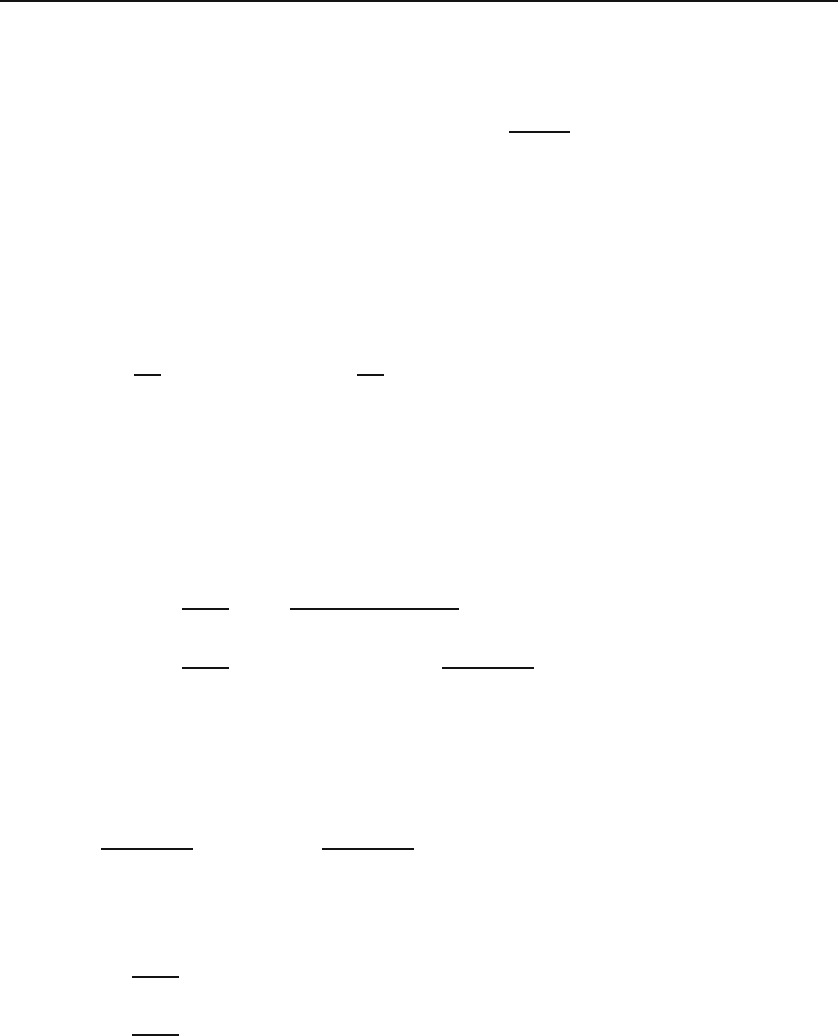
29.2 Fourier Transform and Green’s Functions 709

With the Green’s function of the Laplacian at our disposal, we can solve

the Poisson equation ∇

Φ(r)=−4πk

ρ(r) in electrostatics, using the three-

dimensional version of Equation (29.31):

Green’s function

solves Poisson

equation

Φ(r)=−4πk



G(r − r



)ρ(r



)=k



ρ(r



)

|r − r



which is the electrostatic potential of a charge distribution described by the

volume charge density ρ(r).

29.2.2 Green’s Function for the Heat Equation

The heat equation was given in (22.3), which, due to the special signiﬁcance

attached to the letter k in this chapter, we write as

∂T

∂t

= κ

∇

T (r), or

∂T

∂t

− κ

∇

T (r)=0. (29.38)

This is a PDE in four variables. We let t be the “zeroth” coordinate, and r

the remaining three. Similarly, the 4-dimensional k space consists of k

and

k. The polynomial p(k

) of Equation (29.34) is

p(k

)=ik

+ κ

+ k

≡ ik

+ κ

Hence, with n = 4, (29.34) gives

G(x − x



(2π)

−x



)+ik·(r−r



)

+ κ

(2π)

ik·(r−r



)

∞

−∞

−x



)

+ κ

. (29.39)

Let’s do the k

integration ﬁrst. Multiply the numerator and denominator by

−i to change the denominator to k

−iκ

; then use the calculus of residues

and choose the contour in the UHP (assuming that x

− x



> 0). The only

pole of the integrand is at k

= iκ

.Thus,

∞

−∞

−x



)

+ κ

= −i

∞

−∞

−x



)

− iκ

= −i



2πie

−κ

−x



)



Substituting this in (29.39) and using spherical coordinates in the 3-dimensional

k-space with the polar axis along r −r



yields

G(x − x



(2π)

ik·(r−r



)

−κ

−x



)

(2π)

∞

−κ

−x



)

sin θdθ

2π

dϕe

ik|r−r



|cos θ

The ϕ integration yields 2π, and as in the Laplacian case, the θ integration

gives 2 sin(k|r − r



|)/(k|r − r



|); and since the resulting integrand of the k

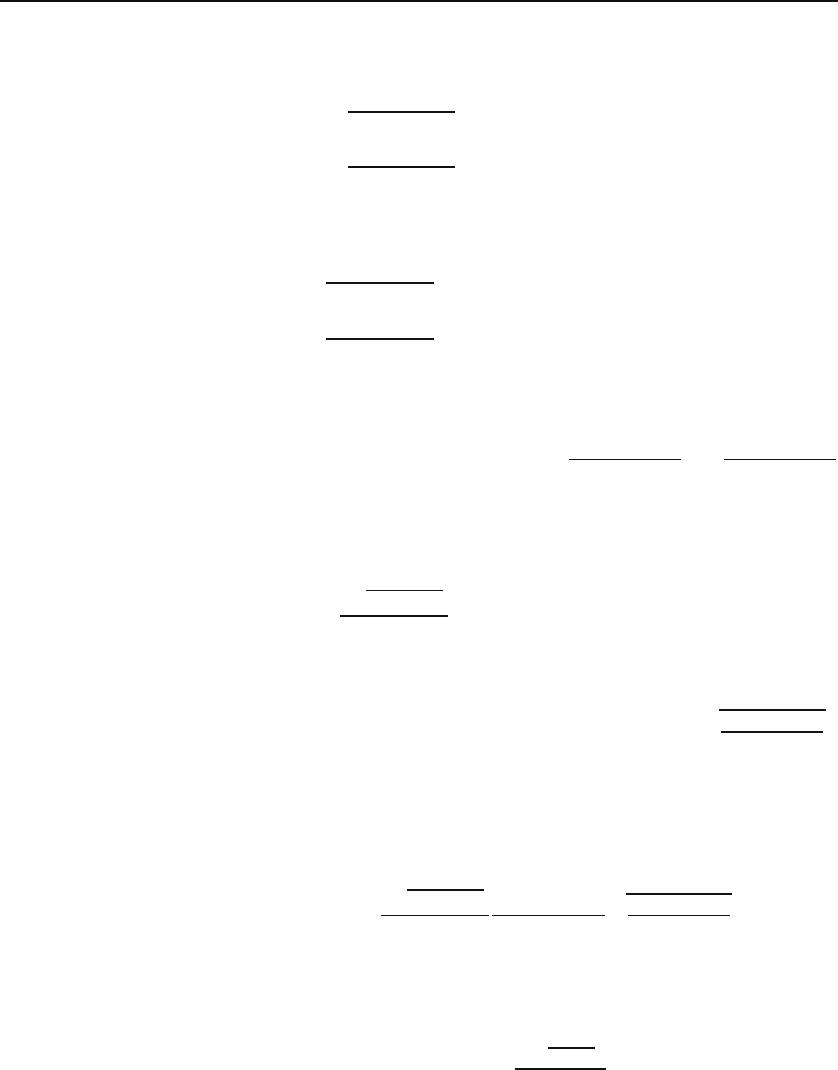
710 Integral Transforms

integral is even, we can extend the lower limit of integration to −∞ and

introducing a factor of half. Thus, the equation above becomes

G(x −x



(2π)

|r − r



∞

−κ

−x



)

sin(k|r − r



|)dk

(2π)

|r − r



∞

−∞

−κ

−x



)

sin(k|r − r



|)dk,

or, since sine is the imaginary part of complex exponential,

G(x −x



(2π)

|r − r



∞

−∞

−κ

−x



)

ik|r−r



(2π)

|r − r



∞

−∞

−κ

−x



)+ik|r−r



dk. (29.40)

Completing the square in the exponent, we have

−κ

−x



)+ik|r−r



| = −κ

−x



)



k −

i|r − r



2κ

− x



)



−

|r − r



4κ

− x



)

Call the imaginary number in the large parentheses iα and substitute the

result in (29.40) to obtain

G(x − x



−

|r−r



4κ

−x



)

(2π)

|r − r



∞

−∞

−κ

−x



)(k−iα)

dk. (29.41)

Change the variable of integration to u = k − iα. Then the integral becomes

∞

−∞

(u + iα)e

−κ

−x



du = iα

∞

−∞

−κ

−x



du = iα



− x



)

The integral involving the u of (u+ iα) vanishes because the integrand is odd.

The Gaussian integral was evaluated in Example 3.3.1. Substituting this and

the value of α in (29.41), we obtain

G(x − x



−

|r−r



4κ

−x



)

(2π)

|r − r



|r − r



2κ

− x



)



− x



)

or, recalling that x

= t and assuming that x



= t



= 0, yields the ﬁnal form

of the Green’s function for the heat equation:

Green’s function

for heat equation

G(r − r



; t)=

−

|r−r



4κ

(4πκ

3/2

. (29.42)