Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

28.2 The Schr¨odinger Equation 679

for some integer N ≥ 0. In that case we obtain the Laguerre polynomials Laguerre

polynomials

≡

Γ(N + j +1)

Γ(N +1)Γ(j +1)

Φ(−N,j +1;z)wherej =2l +1, (28.35)

where the factor in front of Φ is a standardization factor.

Condition (28.34) is the quantization rule for the energy levels of a hydrogen-

Truncation of

inﬁnite series gives

the quantization

rule for the energy

levels of the

hydrogen atom.

like atom. Writing everything in terms of the original parameters, and re-

deﬁning β as β = N + l +1≡ n to reﬂect its integer character, yields—after

restoring all the μ’s and the ’s—the energy levels of a hydrogen-like atom:

E = −

μe

2

= −Z



μc



where α = e

/c =1/137 is the ﬁne structure constant. ﬁne structure

constant

The radial wave functions can now be written as

n,l

(r)=

n,l

(r)

= Cr

−Zr/na



−n + l +1, 2l +2;

2Zr



where a

= 

/me

=0.529 ×10

−8

cm is the Bohr radius.

The explicit form of Laguerre polynomials can be obtained by substitut-

ing the truncated conﬂuent hypergeometric series [see Equation (11.28)] in

(28.35):

(x)=

Γ(N + j +1)

Γ(N +1)Γ(j +1)

Γ(j +1)

Γ(−N)



k=0

Γ(−N + k)

Γ(j +1+k)Γ(k +1)

We now use the result of Problem 11.4 and write

Γ(k − N )

Γ(−N)

=(−1)

N(N − 1) ···(N −k +1)=

(−1)

(N − k)!

It follows that

(x)=

Γ(N + j +1)

Γ(N +1)



k=0

(−1)

(N − k)!

Γ(j +1+k)Γ(k +1)

Simplifying and writing all gamma functions in terms of factorials, we obtain

the ﬁnal form of the Laguerre polynomials:

(x)=



k=0

(N + j)!(−1)

(N −k)!k!(k + j)!

. (28.36)

The generating function of the Laguerre polynomials can be calculated

using a procedure similar to the one used in the case of Hermite polynomials.

We ﬁrst write

(t, x)=

∞



n=0

(x),

680 Other PDEs of Mathematical Physics

diﬀerentiate it with respect to x, and use the result of Problem 28.10 to obtain

= −

∞



n=0

j+1

n−1

(x)=−t

∞



n=0

n−1

j+1

n−1

(x)=−tg

j+1

, (28.37)

wherewehavetakena

= a

n−1

as a natural choice whereby the last sum

could be written in closed form. To ﬁnd a solution of (28.37), we look at

g(t, 0). The recursion relation a

= a

n−1

implies that all a

are equal, and

we set all of them equal to 1. Then

(t, 0) =

∞



n=0

(0) =

∞



n=0

(n + j)!

n!j!

=(1−t)

−j−1

where we used the fact that the only contribution to L

(0) comes from the con-

stant term in the polynomial [corresponding to k = 0 in (28.36)]. Furthermore,

the last sum is the binomial series (10.15) with x →−t and α → (−j − 1).

This suggests deﬁning a new function g(t, x)via

(t, x)=(1−t)

−j−1

g(t, x).

Substitution of this in (28.37) gives

(1 −t)

−j−1

= −t(1 −t)

−j−2

g ⇒

−t

1 − t

dx ⇒ g = C(t)e

−tx/(1−t)

and

(t, x)=(1−t)

−j−1

C(t)e

−tx/(1−t)

C(t)e

−tx/(1−t)

(1 −t)

j+1

With the value of g

(t, 0) given, we determine C(t)tobeone.

Box 28.2.2. The nth coeﬃcient of the Maclaurin series expansion of the

generating function g

(t, x) ≡ (1 − t)

−j−1

−tx/(1−t)

about t =0is L

(x).

Speciﬁcally,

(x)=

∂

∂t

−tx/(1−t)

(1 −t)

j+1



t=0

. (28.38)

28.3 The Wave Equation

In the preceding sections the time variation has been given by a ﬁrst derivative.

Thus, as far as time is concerned, we have a FODE. It follows that the initial

speciﬁcation of the physical quantity of interest (temperature T or Schr¨odinger

wave function ψ) is suﬃcient to determine the solution uniquely.

The wave equation

∇

ψ =

∂

∂t

(28.39)

28.3 The Wave Equation 681

contains time derivatives of the second order, and, therefore, requires two ar-

bitrary parameters in its general solution. To determine these, we expect two

initial conditions. For example, if the wave is standing, as in a rope clamped at

both ends, the initial shape of the rope is not suﬃcient to determine the wave

function uniquely. One also needs to specify the initial (transverse) velocity

of each point of the rope, i.e., the velocity proﬁle on the rope.

Example 28.3.1.

one-dimensional wave one-dimensional

waveThe simplest kind of wave equation is that in one dimension, for example, a wave

propagating on a rope. Such a wave equation can be written as

∂

∂x

∂

∂t

where c is the speed of wave propagation. For a rope, this speed is related to the

tension τ and the linear mass density ρ by c =



τ/ρ.

Let us assume that the rope has length a and is fastened at both ends (located

at x =0andx = a). This means that the “displacement” ψ is zero at x =0andat

x = a.

A separation of variables, ψ(x, t)=X(x)T (t), leads to two ODEs:

+ λX =0,

+ c

λT =0. (28.40)

The ﬁrst equation and the spatial boundary conditions give rise to the solutions

(x)=sin



nπ



,λ



nπ



for n =1, 2,....

The second equation in (28.40) has a general solution of the form

T (t)=A

cos ω

t + B

sin ω

where ω

= cnπ/a and A

and B

are arbitrary constants. The general solution is

thus

ψ(x, t)=

∞



n=1

cos ω

t + B

sin ω

t)sin



nπx



. (28.41)

Speciﬁcation of the initial shape of the rope as ψ(x, 0) = f(x) gives a Fourier

series,

f(x)=

∞



n=1

sin



nπx



from which we can determine A

f(x)sin



nπx



dx.

What about B

? Physically, the shape of the wave is not enough to deﬁne the

problem uniquely. It is possible that the rope, while having the required initial

shape, may be in an unspeciﬁed motion of some sort. Thus, we must also know the

“velocity proﬁle,” which means specifying the function ∂ψ/∂t at t =0. Ifitisgiven

682 Other PDEs of Mathematical Physics

that ∂ψ/∂t|

t=0

= g(x), then diﬀerentiating (28.41) with respect to t and evaluating

both sides at t =0yields

g(x)=

∞



n=1

sin



nπx



and B

is also determined:

aω

g(x)sin



nπx



dx.

The frequency ω

is referred to as that of the nth mode of oscillation.Thusmode of

oscillation a general solution is a linear superposition of inﬁnitely many modes. In practice,

it is possible to “excite” one mode or, with appropriate initial conditions, a ﬁnite

number of modes.



28.3.1 Guided Waves

Waveguides are hollow tubes (or tubes ﬁlled with some dielectric material) in

which electromagnetic waves can propagate along an axis which we take to

be the z-axis of either Cartesian or cylindrical coordinates. We assume that

the dependence of the electric and magnetic ﬁelds on z and t is of the form

i(ωt−kz)

where ω and k are constants to be determined. We therefore write

E = E

(x, y)e

i(ωt−kz)

, B = B

(x, y)e

i(ωt−kz)

, (28.42)

for Cartesian coordinates. If cylindrical geometry is appropriate, then E

and

will be functions of ρ and ϕ. Note that, in general, E

and B

have three

components.

The electric and magnetic ﬁelds of (28.42) ought to satisfy the four Maxwell’s

equations. Let us assume that the waveguide is free of any charges or cur-

rents, so that Maxwell’s equations for empty space are appropriate. Because

of the nature of the dependence on z, it is useful to separate the longitudi-

nal geometry—the geometry along z—from the transverse geometry—the

longitudinal and

transverse parts of

guided waves.

geometry perpendicular to z.So,wewrite

E = E

=(E

i(ωt−kz)

B = B

=(B

i(ωt−kz)

, (28.43)

∇ =

∂

∂x

∂

∂y

∂

∂z

≡ ∇

∂

∂z

where the subscript t stands for transverse. With these assumptions, Maxwell’s

ﬁrst equation becomes

0=∇· E =



∇

∂

∂z



i(ωt−kz)

=(∇

·E

) e

i(ωt−kz)

+(−ikE

) e

i(ωt−kz)

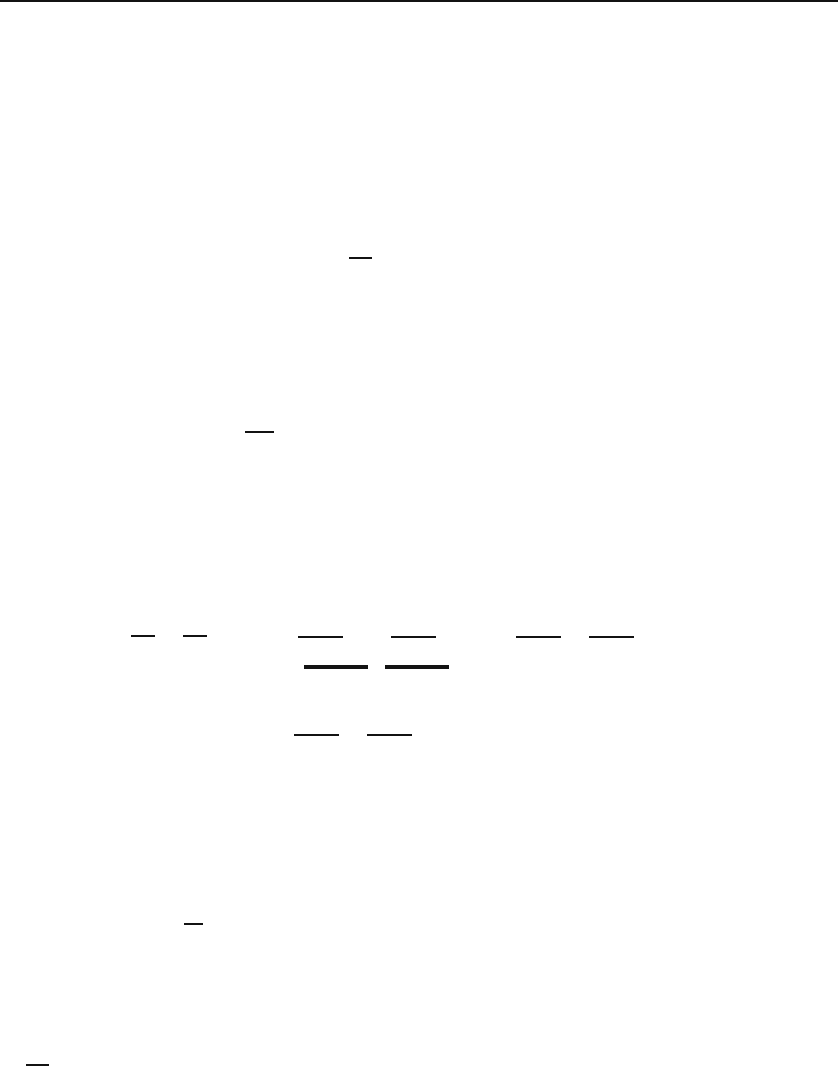
28.3 The Wave Equation 683

because ∇

· (

)=0and

·E

= 0. It follows that

∇

·E

= ikE

An analogous calculation gives a similar result for Maxwell’s second equation.

Putting these two equations together, we get

∇

·E

= ikE

, ∇

· B

= ikB

. (28.44)

The LHS of Maxwell’s third equation gives

LHS = ∇ ×E =



∇

∂

∂z



i(ωt−kz)

= ∇

i(ωt−kz)

−ikE

i(ωt−kz)

= e

i(ωt−kz)

(∇

× E

− ik

× E

) .

TheRHSofthethirdequationis

−

∂B

∂t

= −iωB

i(ωt−kz)

Equating the two sides yields

−iωB

= ∇

× E

− ik

× E

. (28.45)

The ﬁrst term on the RHS can be written as

∇

× E



∂

∂x

∂

∂y



∂E

∂y

−

∂E

∂x

  

This is transverse.



∂E

∂x

−

∂E

∂y



= ∇ × (E



∂E

∂x

−

∂E

∂y



The reader may easily check that the second line follows from the ﬁrst. Equat-

ing the transverse parts of the two sides of Equation (28.45), we get

−iωB

= ∇ × (E

) −ik

× E

. (28.46)

A similar calculation turns the fourth Maxwell equation into

= ∇ ×(B

) −ik

× B

. (28.47)

We now want to express the transverse components in terms of the lon-

gitudinal components. Multiply both sides of (28.47) by −iω and substitute

for −iωB

from (28.46):

= −iω∇× (B

) −ik

× [∇ × (E

) −ik

× E

]

= −iω∇× (B

) −ik

× [∇ × (E

)] −k

× (

× E

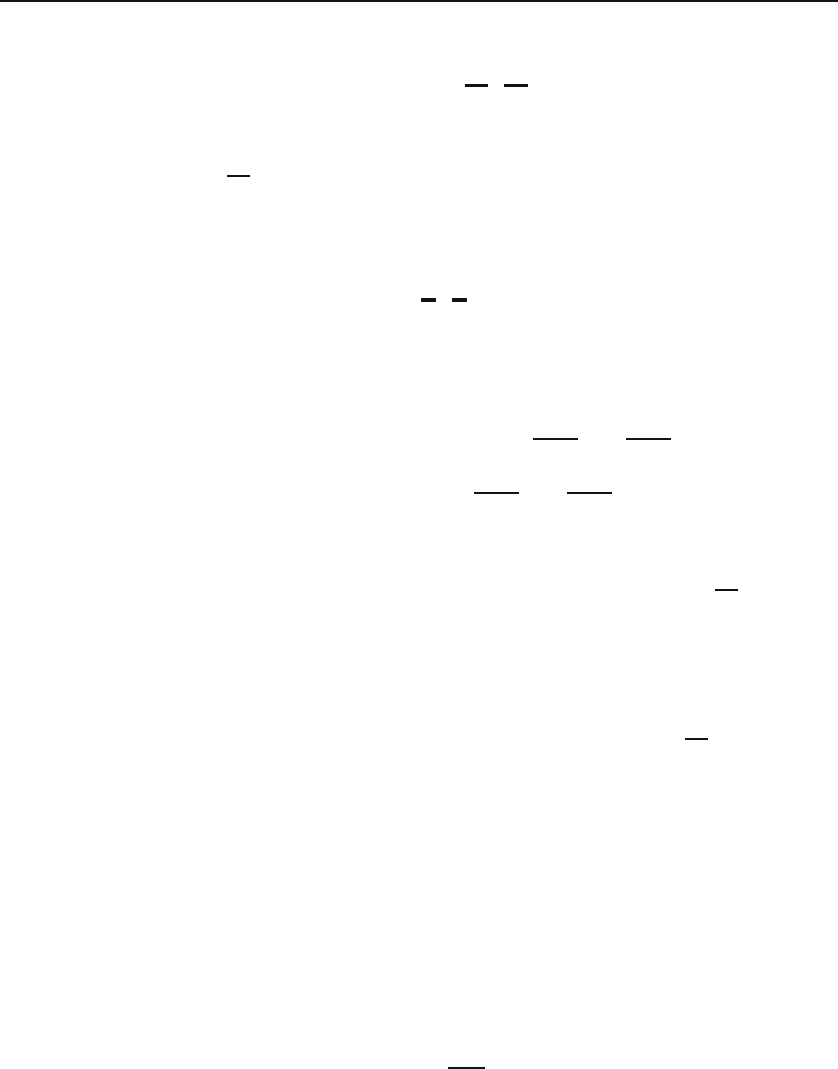
684 Other PDEs of Mathematical Physics

Using the bac cab rule, the last term gives

× (

× E

(

· E

)



 

−E

(

)=−E

It now follows that



− k



= −iω∇× (B

) −ik

× [∇ × (E

)] . (28.48)

The ﬁrst term on the RHS can be simpliﬁed by using the second equation in

(14.11):

∇ × (B

)=B

∇ ×

  

+(∇B

) ×

= −

× (∇

)

because

is a constant vector (both magnitude and direction), and B

independent of z. The second term on the RHS of (28.48) can be simpliﬁed

as follows:

× [∇ × (E

)] =



∂E

∂y

−

∂E

∂x



∂E

∂y

∂E

∂x

≡ ∇

Substituting these results in Equation (28.48) yields

= i [−k∇

+ ω

× (∇

)] where γ

≡

− k

A similar calculation gives an analogous result for the magnetic ﬁeld. We

assemble these two equations in

= i [−k∇

+ ω

× (∇

)] , (28.49)

= i [−k∇

− ω

× (∇

)] ,γ

≡

− k

Although we derived (28.44) and (28.49) using Cartesian coordinates, the

fact that the ﬁnal result is written explicitly in terms of transverse and lon-

gitudinal parts—without reference to any coordinate system—implies that

these equations are valid in cylindrical coordinates as well.

Three types of guided waves are usually studied.

1. Transverse magnetic (TM) waves have B

= 0 everywhere. The bound-transverse

magnetic (TM)

waves

ary condition on E demands that E

vanish at the conducting walls of

the guide.

2. Transverse electric (TE) waves have E

= 0 everywhere. The boundarytransverse electric

(TE) waves

condition on B requires that the normal directional derivative

∂B

∂n

≡

·(∇B

)

vanish at the walls.

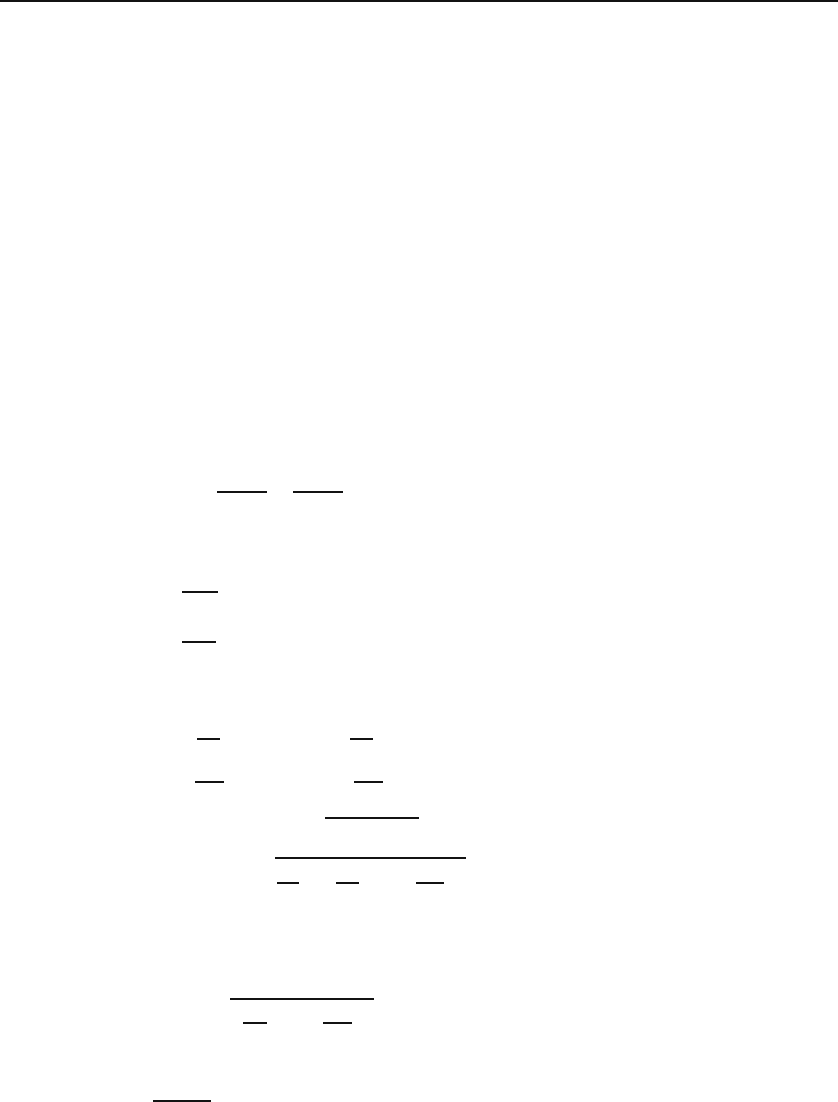
28.3 The Wave Equation 685

3. Transverse electromagnetic (TEM) waves have B

=0=E

.Fora transverse

electromagnetic

(TEM) waves

nontrivial solution, Equation (28.49) demands that γ

=0. Thisform

resembles a free wave with no boundaries.

In the following, we consider some examples of the TM mode (see any

book on electromagnetic theory for further details). The basic equations in

this mode are

=0,γ

= −ik∇

,γ

= −iω

× (∇

Taking the dot product of ∇

with the middle equation and using the ﬁrst

equation in (28.44) yields

Basic equation for

TM waves.

∇

+ γ

=0. (28.50)

This is the basic equation for TM waves propagating in a waveguide.

Example 28.3.2.

rectangular wave guides rectangular wave

guidesFor a wave guide with a rectangular cross section of sides a and b in the x and the

y direction, respectively, (28.50) gives

∂

∂x

∂

∂y

+ γ

=0.

A separation of variables, E

(x, y)=X(x)Y (y), leads to

+ λX =0,X(0) = 0 = X(a),

+ μY =0,Y(0) = 0 = Y (b),

where γ

= λ + μ. These equations have the solutions

(x)=sin



nπ



,λ



nπ



for n =1, 2,...,

(y)=sin



mπ



,μ



mπ



for m =1, 2,....

Thewavenumberisgivenbyk =



(ω/c)

− γ

, or, introducing indexes for k,



−



nπ



−



mπ



which has to be real if the wave is to propagate [an imaginary k leads to exponential

decay or growth along the z-axis because of the exponential factor in (28.49)]. Thus,

there is a cut-oﬀ frequency,

= c





nπ





mπ



for m, n ≥ 1,

below which the wave cannot propagate through the wave guide. It follows that,

for a TM wave, the lowest frequency that can propagate along a rectangular wave

guide is ω

= πc

√

+ b

/ab.

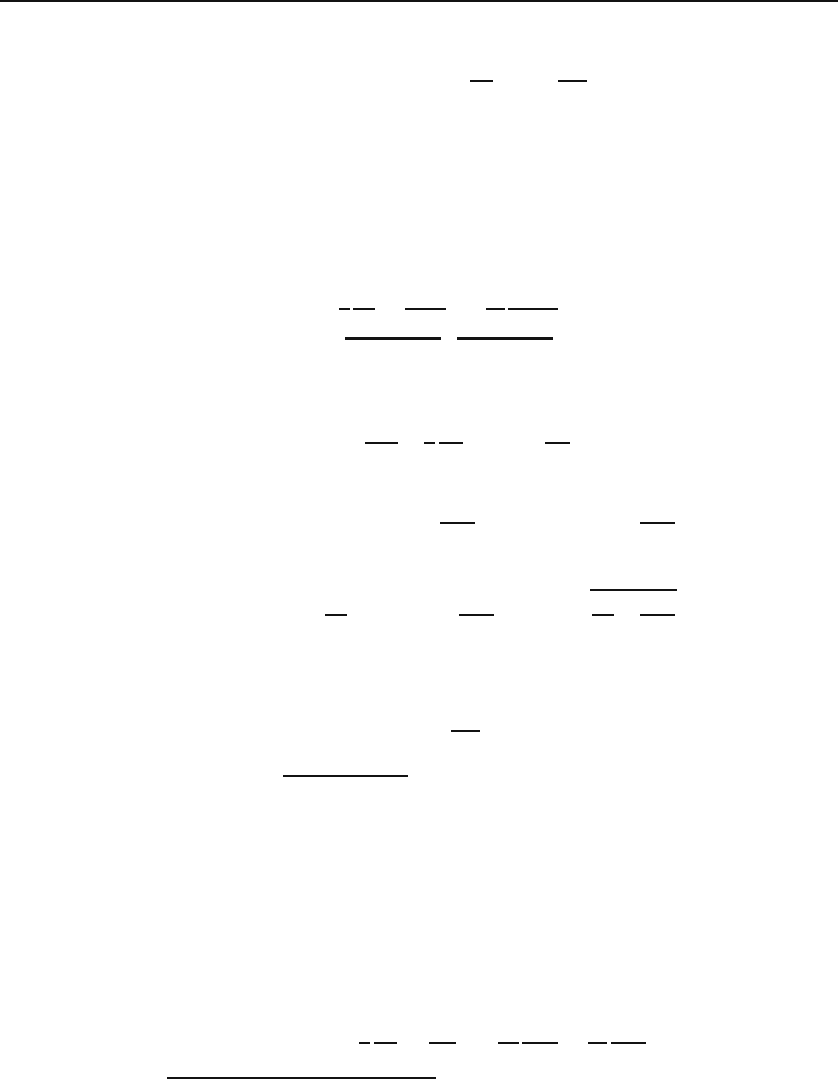
686 Other PDEs of Mathematical Physics

The most general solution for E

is, therefore,

∞



m,n=1

sin



nπ



sin



mπ



i(ωt±k

The constants A

are arbitrary and can be determined from the initial shape of

the wave, but that is not commonly done. Once E

is found, the other components

can be calculated using Equation (28.50).



Example 28.3.3. cylindrical wave guidecylindrical wave

guide For a TM wave propagating along the z-axis in a hollow circular conductor, we have

[see Equation (28.50)]

∂

∂ρ



∂E

∂ρ



∂

∂ϕ

  

≡∇

+ γ

=0.

The separation E

= R(ρ)S(ϕ) yields S(ϕ)=A cos mϕ + B sin mϕ and the Bessel

dρ



−



R =0.

The solution to this equation, which is regular at ρ = 0 and vanishes at ρ = a,is

R(ρ)=CJ





and γ =

Recalling the deﬁnition of γ,weobtain

− k

= γ

⇒ k =



−

This gives the cut-oﬀ frequency ω

= cx

/a.

The solution for the azimuthally symmetric case (m =0)is

(ρ, ϕ, t)=

∞



n=1





i(ωt±k

and B

=0,

where k



− x



28.3.2 Vibrating Membrane

Waves on a circular drumhead are historically important because their inves-

tigation was one of the ﬁrst instances in which Bessel functions appeared. The

following example considers such waves.

For a circular membrane over a cylinder, the wave equation (28.39) in

cylindrical coordinates becomes

∂

∂ρ



∂ψ

∂ρ



∂

∂ϕ

∂

∂t

Assuming that the membrane is perpendicular to the z-axis, the wave amplitude will

depend only on ρ and ϕ.

28.4 Problems 687

which, after separation of variables, reduces to

S(ϕ)=A cos mϕ + B sin mϕ for m =0, 1, 2,...,

T (t)=C cos ωt + D sin ωt,

dρ



−



R =0.

The solution of the last (Bessel) equation, which is deﬁned for ρ =0and

vanishes at ρ = a,is

R(ρ)=EJ





where

and n =1, 2,....

This shows that only the frequencies ω

=(c/a)x

are excited.

If we assume an initial shape for the membrane, given by f(ρ, ϕ), and an

initial velocity of zero, then D = 0, and the general solution will be

ψ(ρ, ϕ, t)=

∞



m=0

∞



n=1





cos





cos mϕ + B

sin mϕ),

where

πa

m+1

)

2π

dϕ

dρ ρf (ρ, ϕ)J





cos mϕ,

πa

m+1

)

2π

dϕ

dρ ρf (ρ, ϕ)J





sin mϕ,

and the orthogonality of Bessel functions (27.24) has been used. In particular,

if the initial displacement of the membrane is independent of ϕ, then only the

term with m = 0 contributes, and we get

ψ(ρ, t)=

∞



n=1





cos





where

)

dρ ρf (ρ)J





Note that the wave does not develop any ϕ-dependence at later times.

28.4 Problems

28.1. Suppose λ = 0 in Equation (28.3). Show that X(x)=0.

28.2. The two ends of a thin heat-conducting bar are held at T = 0. Initially,

the ﬁrst half of the bar is held at T = T

, and the second half is held at

T = 0. The lateral surface of the bar is then thermally insulated. Find the

temperature distribution for all time.

688 Other PDEs of Mathematical Physics

28.3. The two ends of a thin heat-conducting bar of length b are held at

T = 0. The bar is along the x-axis with one end at x = 0 and the other

at x = b. The lateral surface of the bar is thermally insulated. Find the

temperature distribution at all times if initially it is given by:

(a) T (0,x)=

for the middle third of the bar,

0 for the other two-thirds.

(b) T (0,x)=

⎧

⎪

⎨

⎪

⎩

0if0≤ x ≤

≤ x ≤ b,

sin



3π

x − π



≤ x ≤



−



−

(d) T (0,x)=T

sin





28.4. Derive Equation (28.7) from the equation before it by changing variables.

28.5. Using the Stirling approximation (11.6), write all four factorials of

Equation (28.14) as exponentials. Then simplify to arrive at Equation (28.15).

28.6. Derive Equations (28.20)–(28.23).

28.7. By diﬀerentiating both sides of Equation (28.23) with respect to y,and

(slightly) manipulating the resulting sum, show that H



(y)=2nH

n−1

(y).

28.8. Evaluate Equation (28.23) at y = 0 and note that only the last term

survives. Now show that

(0) =

⎧

⎨

⎩

0ifn is odd,

(−1)

(2k)!

if n =2k.

28.9. Use the substitution u(z)=z

l+1

−z/2

f(z) in (28.32) to derive Equation

(28.33).

28.10. Diﬀerentiate both sides of Equation (28.36) with respect to x and

show that

(x)=−L

j+1

N−1

(x).

28.11. The two ends of a rope of length a are ﬁxed. The midpoint of the

rope is raised a distance a/2, measured perpendicular to the tense rope, and

released from rest. What is the subsequent wave function?

28.12. Astringoflengtha fastened at both ends has an initial velocity of

zero and is given an initial displacement as shown in Figure 28.1. Find ψ(x, t)

in each case.