Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

648 Laplace’s Equation: Cylindrical Coordinates

where the prime indicates diﬀerentiation with respect to ρ. Now integrate

this equation with respect to ρ from some initial value (say a) to some ﬁnal

value (say b)toobtain

[ρ(fg



− gf



)]

=(k

− l

)

ρf(ρ)g(ρ) dρ.

In all physical applications a and b can be chosen to make the LHS vanish.

Then, substituting for f and g in terms of Bessel functions, we get

− l

)

ρJ

(kρ)J

(lρ) dρ =0.

It follows that if k = l, then the integral vanishes, i.e.,

ρJ

(kρ)J

(lρ) dρ =0 if k = l. (27.20)

This is the orthogonality relation for Bessel functions also derived in Example

24.5.3.

To complete the orthogonality relation, we must also address the case when

k = l. This involves the evaluation of the integral



ρJ

(kρ) dρ,which,upon

the change of variable x ≡ kρ, reduces to (



(x) dx)/k

.Byintegration

by parts, we have

I ≡

(x)



 

xdx





(x) −

(x)J



(x)x

dx.

In the last integral, substitute for x

(x) from the Bessel DE (27.6)—using

x instead of v:

(x)=m

(x) −xJ



(x) −x



(x).

Therefore,

I =

(x) −



(x)[m

(x)

=−(



(x)]

)



  

−xJ



(x) −x



(x)] dx

(x) − m

(x)]



  

(x)J



(x) dx +



(x)]

(x) −

(x)+



(x)]

Returning back to ρ, we obtain the indeﬁnite integral

ρJ

(kρ) dρ =



−



(kρ)+



(kρ)]

. (27.21)

27.4 Properties of the Bessel Functions 649

In most applications, the lower limit of integration is zero and the upper limit

is a positive number a. The RHS of (27.21) vanishes at the lower limit because

of the following reason. The ﬁrst term vanishes at ρ = 0 because J

(0) = 0

for all m>0 as is evident from the series expansion (27.10). For m =0(and

ρ = 0), the parentheses in the ﬁrst term of (27.21) vanishes. So, the ﬁrst

term is zero for all m ≥ 0 at the lower limit of integration. The second term

vanishes due to the presence of ρ

.Thus,weobtain

ρJ

(kρ) dρ =



−



(ka)+



(ka)]

(27.22)

for all m ≥ 0 and, by (27.14), also for all negative integers. As mentioned

earlier, we shall conﬁne our discussion to Bessel functions of integer orders.

It is customary to simplify the RHS of (27.22) by choosing k in such a way

that J

(ka) = 0, i.e., that ka is a root of the Bessel function of order m.In

general, there are inﬁnitely many roots. So, let x

denote the nth root of

(x). Then,

ka = x

⇒ k =

,n=1, 2,...,

and if we use Equation (27.17), we obtain

ρJ

ρ/a) dρ =

m+1

)]

. (27.23)

Equations (27.20) and (27.23) can be combined into a single equation using

the Kronecker delta:

orthogonality

relations involving

Bessel functions

Box 27.4.1. The Bessel functions of integer order satisfy the orthogonal-

ity relations

ρ/a)J

ρ/a)ρdρ =

m+1

)δ

, (27.24)

where a>0 and x

is the nth root of J

(x).

27.4.4 Generating Function

Just as in the case of Legendre polynomials, Bessel functions of integer order

have a generating function, i.e., there exists a function g(x, t) such that

g(x, t)=

∞



n=−∞

(x). (27.25)

To ﬁnd g, start with the recurrence relation

m−1

(x)+J

m+1

(x)=

(x),

650 Laplace’s Equation: Cylindrical Coordinates

multiply it by t

,andsumoverallm to obtain

∞



m=−∞

m−1

(x)+

∞



m=−∞

m+1

(x)=

∞



m=−∞

(x). (27.26)

The ﬁrst sum can be written as

∞



m=−∞

m−1

(x)=t

∞



m=−∞

m−1

(x)=t

∞



n=−∞

(x)=tg(x, t),

where we substituted the dummy index n = m −1form. Similarly

∞



m=−∞

m+1

(x)=

∞



m=−∞

m+1

(x)=

g(x, t)

and

∞



m=−∞

(x)=

∞



m=−∞

m−1

(x)=

∂g

∂t

It follows from Equation (27.26) that



t +



g(x, t)=

∂g

∂t





dt =

where x is assumed to be a constant because we have been diﬀerentiating with

respect to t. Integrating both sides gives







 

(

t−

)

=lng +lnφ(x),

where the last term is the “constant” of integration. Thus,

g(x, t)=φ(x)exp





t −



To determine φ(x), we note that

g(x, t)=φ(x)e

xt/2

−x/2t

= φ(x)

∞



n=0

(xt/2)

∞



m=0

(−x/2t)

= φ(x)

∞



n,m=0

(−1)

n!m!





n+m

n−m

27.4 Properties of the Bessel Functions 651

In the last double sum, collect all terms whose power of t is zero, and call the

sum S

. This is obtained by setting n = m. Then,

= φ(x)

∞



n=0

(−1)

n!n!





= φ(x)J

(x),

where we used Equation (27.10) with s = 0. But (27.25) shows that the

collection of all terms whose power of t is zero is simply J

(x). Thus, S

(x), and φ(x) = 1. This leads to the ﬁnal form of the Bessel generating

function:

generating

function for Bessel

functions

g(x, t)=exp





t −



∞



n=−∞

(x). (27.27)

Example 27.4.1.

The generating function for Bessel functions can be used to

obtain a useful identity. First we note that

g(x + y, t)=g(x, t)g(y,t)

as the reader may easily verify. Expanding each side gives

∞



n=−∞

(x + y)=

∞



k=−∞

(x)

∞



m=−∞

(y)=

∞



k=−∞

∞



m=−∞

k+m

(x)J

(y).

In the last double sum, let n = k+m,sothatk = n−m. Since there is no limitation

on the value of either of the dummy indices, the limits of the new indices n and m

are still −∞ and ∞. Therefore,

∞



n=−∞

(x + y)=

∞



n=−∞

∞



m=−∞

n−m

(x)J

(y)

∞



n=−∞



∞



m=−∞

n−m

(x)J

(y)



Since each power of t should have the same coeﬃcient on both sides, we obtain the

so-called addition theorem for Bessel functions: addition theorem

for Bessel

functions

(x + y)=

∞



m=−∞

n−m

(x)J

(y)=

∞



m=−∞

(x)J

n−m

(y), (27.28)

where the last equality follows from the symmetry of J

(x + y) under the exchange

of x and y.



The Bessel generating function can also lead to some very important iden-

tities. In Equation (27.27), let t = e

iθ

and use (18.14) to obtain

ix sin θ

∞



n=−∞

inθ

(x). (27.29)

652 Laplace’s Equation: Cylindrical Coordinates

This is a Fourier series expansion in θ—as given in (18.20)—whose coeﬃcients

are Bessel functions. To ﬁnd these coeﬃcients, we multiply both sides by

−imθ

and integrate from −π to π [see also Equation (18.22)]. The LHS

gives

LHS =

−π

ix sin θ

−imθ

dθ =

−π

i(x sin θ−mθ)

dθ.

For the RHS, we obtain

∞



n=−∞



−π

i(n−m)θ

dθ



(x)=2πJ

(x),

where we used the easily veriﬁable result [also see Equation (18.21)]:

−π

i(n−m)θ

dθ =

0ifn = m

2π if n = m

=2πδ

Equating the RHS and the LHS, we obtain

integral

representation of

the Bessel

function

(x)=

2π

−π

i(x sin θ−mθ)

dθ. (27.30)

The reader may check that this can be reduced to

(x)=

cos(x sin θ − mθ) dθ (27.31)

which is called Bessel’s integral.

Bessel’s integral

Bessel functions can be written in terms of the conﬂuent hypergeometric

function. To see this, substitute R(v)=v

−ηv

f(v)—with μ and η to be

determined—in Equation (27.6) to obtain



2μ +1

− 2η





− m

−

η(2μ +1)

+ η



f =0

which, if we set μ = m and η = i, reduces to





2m +1

− 2i





−

(2m +1)i

f =0. (27.32)

Making the further substitution 2iv = t, and multiplying out by t,weobtain

+(2m +1− t)

− (m +

)f =0

which is in the form of (11.27) with α = m +

and γ =2m + 1. Thus, Bessel

functions J

(x) can be written as constant multiples of x

−ix

Φ(m+

, 2m+relation between

Bessel functions

and conﬂuent

hypergeometric

function

1; 2ix). In fact,

(x)=

Γ(m +1)





−ix

Φ(m +

, 2m +1;2ix). (27.33)

27.5 Expansions in Bessel Functions 653

27.5 Expansions in Bessel Functions

The orthogonality of Bessel functions can be useful in expanding other func-

tions in terms of them. The basic idea is similar to the expansion in Fourier

series and Legendre polynomials. If a function f(ρ) is deﬁned in the interval

(0,a), then we may write

f(ρ)=

∞



n=1

ρ/a). (27.34)

The coeﬃcients can be found by multiplying both sides by ρJ

ρ/a)and

integrating from zero to a. The reader may verify that this yields

m+1

)

f(ρ)J

ρ/a)ρdρ. (27.35)

Equations (27.34) and (27.35) are the analogues of Equations (10.38),

(10.40), (10.41), and (10.42) for Fourier series, and Equations (26.46) and

(26.47) for Legendre polynomials. Like those sets of equations, they can be

used to expand functions in terms of Bessel functions of a speciﬁc order.

Example 27.5.1.

The trigonometric functions can be expanded in Bessel func-

tions with very little eﬀort. In fact, Equation (27.29) leads immediately to

∞



n=−∞

(x)

or expansion of sine

and cosine in

Bessel functions

cos x + i sin x =

∞



k=−∞

(x)+

∞



k=−∞

2k+1

(x),

wherewehaveseparatedtheevenandoddsums. Theﬁrstsumisrealandthe

second sum pure imaginary. Therefore,

cos x =

∞



k=−∞

(−1)

(x)=

−1



k=−∞

(−1)

(x)+J

(x)+

∞



k=1

(−1)

(x).

The ﬁrst sum can be written as

−1



k=−∞

(−1)

(x)=

∞



k=1

(−1)

−k

−2k

(x)=

∞



k=1

(−1)

(x)

∞



k=1

(−1)

(x)

which is identical to the last sum. It follows that

cos x = J

(x)+2

∞



k=1

(−1)

(x). (27.36)

Similarly,

sin x =2

∞



k=0

(−1)

2k+1

(x) (27.37)

as the reader is urged to verify.



654 Laplace’s Equation: Cylindrical Coordinates

If we square Equation (27.34), multiply by ρ, and integrate from zero to

a,weobtain

(ρ)ρdρ =

∞



n=1

∞



k=1

ρ/a)J

ρ/a)ρdρ

  

m+1

)δ

by (27.24)

This leads to the so-called Parseval relation:

Parseval relation

(ρ)ρdρ =

∞



n=1

m+1

) (27.38)

for some m.Thism can be chosen to make the integrations as simple as

possible.

Example 27.5.2.

Let us ﬁnd the expansion of ρ

in terms of Bessel functions.expansion of ρ

terms of Bessel

functions

Equations (27.35) and (27.18) suggest expanding in terms of J

(x)becausethe

integrals can be performed. Therefore, we write

∞



n=1

ρ/a),

where

k+1

)

ρ/a)ρdρ =

k+1

)

k+1

ρ/a) dρ.

Introducing y = x

ρ/a in the integral gives

k+2

k+1

)

k+1

(y) dy =

k+1

)

where we used (27.18) with m replaced by k +1. Thus, we have

=2a

∞



n=1

ρ/a)

k+1

)



27.6 Physical Examples

Our discussion of Laplace’s equation has led us to believe that trigonometric

functions and Legendre polynomials are, respectively, the “natural” functions

of Cartesian and spherical geometries. It is of no surprise now to learn that

Bessel functions are the natural functions of cylindrical geometry.

As in the case of Cartesian and spherical coordinates, unless the symmetry

of the problem simpliﬁes the situation, the separation of Laplace’s equation

results in two parameters leading to a double sum as in Example 25.2.4. The

reason that we did not obtain double sums in spherical coordinates is that

from the very beginning we assumed azimuthal symmetry. Thus, we expect

27.6 Physical Examples 655

ρ, φ

)

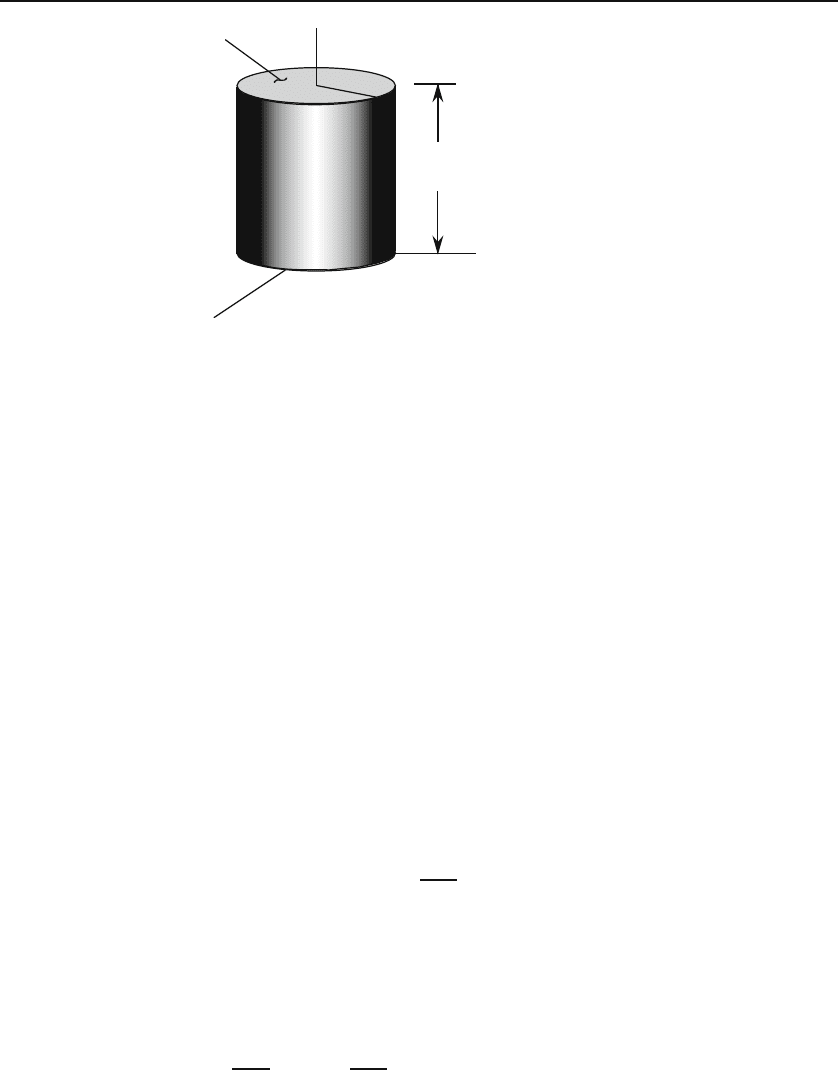
Figure 27.1: A conducting cylindrical can whose top has a potential given by V (ρ, θ)

with the rest of the surface grounded.

a double summation in the most general solution of Laplace’s equation in

cylindrical geometries. One of these sums is over m which, as Equation (27.3)

shows, appears in the argument of the sine and cosine functions. It also

designates the order of the Bessel (or Neumann) function.

To understand the origin of the second summation, consider a cylindrical

conducting can of radius a and height h (see Figure 27.1). Suppose that the

potential at the top face varies as V (ρ, ϕ) while the lateral surface and the

bottom face are grounded. Let us ﬁnd the electrostatic potential Φ at all

points inside the can.

The general solution is a product of (27.3), (27.4), and (27.13):

Φ(ρ, ϕ, z)=R(ρ)S(ϕ)Z(z).

Since Φ(ρ, ϕ, 0) = 0 for arbitrary ρ and ϕ,wemusthaveZ(0) = 0 yielding—to

within a constant—Z(z) = sinh(lz).

Since Φ(0,ϕ,z) is ﬁnite, no Neumann function is allowed in the expan-

sion, and, to within a constant, we have R(ρ)=J

(lρ). Furthermore, since

Φ(a, ϕ, z) = 0 for arbitrary ϕ and z,wemusthave

R(a)=J

(la)=0 ⇒ la = x

⇒ l =

,n=1, 2,...,

where, as before, x

is the nth root of J

We can now multiply R, S,andZ and sum over all possible values of m

and n, keeping in mind that negative values of m give terms that are linearly

dependent on the corresponding positive values. The result is the so-called

Fourier–Bessel series:

Fourier–Bessel

series

Φ(ρ, ϕ, z)=

∞



m=0

∞



n=1





sinh





cos mϕ + B

sin mϕ)

(27.39)

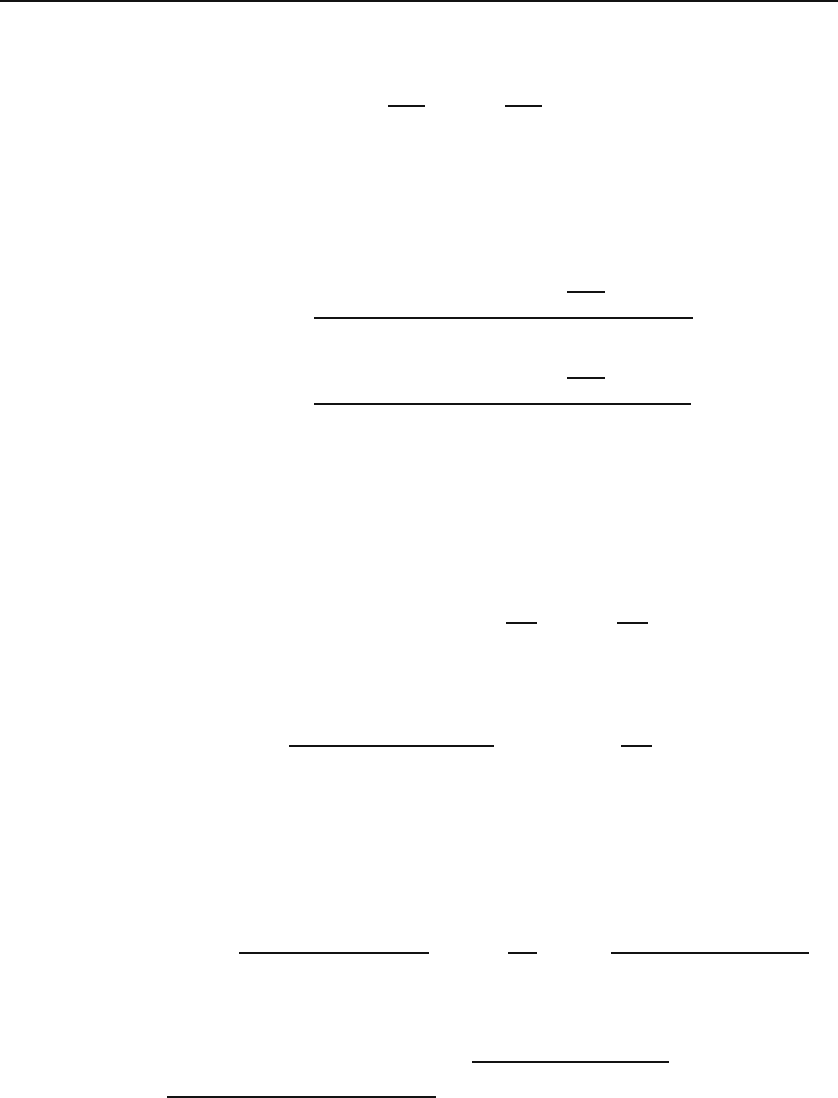
656 Laplace’s Equation: Cylindrical Coordinates

where A

and B

are constants to be determined by the remaining bound-

ary condition which states that Φ(ρ, ϕ, h)=V (ρ, ϕ)or

V (ρ, ϕ)=

∞



m=0

∞



n=1





sinh





cos mϕ + B

sin mϕ).

(27.40)

Multiplying both sides by ρJ

a/ρ)cosjϕ and integrating from zero to

2π in ϕ, and from zero to a in ρ gives A

. Changing cosine to sine and

following the same steps yields B

. Switching back to m and n,thereader

may verify that

2π

dϕ

dρ ρV (ρ, ϕ)J





cos mϕ

πa

m+1

) sinh(x

h/a)

2π

dϕ

dρ ρV (ρ, ϕ)J





sin mϕ

πa

m+1

)sinh(x

h/a)

, (27.41)

where we have used Equation (27.24).

The important case of azimuthal symmetry requires special consideration.

In such a case, the potential of the top surface V (ρ, ϕ) must be independent

of ϕ. Furthermore, since S(ϕ) is constant,

its derivative must vanish. Hence,

the second equation in (27.1) yields μ = −m

= 0. This zero value for m

reduces the double summation of (27.39) to a single sum, and we get

Φ(ρ, z)=

∞



n=1





sinh





. (27.42)

The coeﬃcients A

can be obtained by setting m = 0 in the ﬁrst equation of

(27.41):

) sinh(x

h/a)

ρV (ρ)J





dρ, (27.43)

where V (ρ)istheϕ-independent potential of the top surface.

Example 27.6.1.

Suppose that the top face of a conducting cylindrical can is

held at the constant potential V

while the lateral surface and the bottom face are

grounded. We want to ﬁnd the electrostatic potential Φ at all points inside the can.

Since the potential of the top is independent of ϕ, azimuthal symmetry prevails,

and Equation (27.43) gives

) sinh(x

h/a)

ρJ





dρ =

) sinh(x

h/a)

where we used Equation (27.18). The detail of calculating the integral is left as

Problem 27.15 for the reader. Therefore,

Φ(ρ, z)=4V

∞



n=1

ρ/a) sinh(x

z/a)

) sinh(x

h/a)



S(ϕ) must be a constant. Otherwise, the potential would depend on ϕ.

27.7 Problems 657

27.7 Problems

27.1. Derive (27.6) from the ﬁrst equation of (27.1).

27.2. Show that both equations in (27.17) give



(x)=−J

(x).

27.3. Show that

−m

(x)]



= −x

−m

m+1

(x)

and derive Equation (27.19).

27.4. Obtain the following equation from the Bessel DE:

dρ

[ρ(fg



− gf



)] = (k

− l

)ρfg,

where f and g are solutions of two Bessel DEs for which the “constants” of

the DEs are k

and l

, respectively.

27.5. (a) Show that for the Bessel generating function,

g(x + y, t)=g(x, t)g(y,t)andg(x, −t)=

g(x, t)

(b) Use the second relation to show that

∞



m=−∞

m−k

(x)J

(x)=δ

≡

1ifk =0,

0ifk =0.

Hint: Set the powers of t equal on both sides of 1 = g(x, t)g(x, −t).

∞



m=−∞

(x)=J

(x)+2

∞



m=1

(x),

showing that |J

(x)|≤1and|J

(x)|≤1/

√

2form>0.

27.6. Derive Equation (27.31) from (27.30).

27.7. Use Equation (27.31) to show that J

−m

=(−1)

27.8. Show that the substitution R(v)=v

−iv

f(v) turns Equation (27.6)

into (27.32).

27.9. Using the orthogonality of Bessel functions derive Equation (27.35)

from (27.34).

27.10. Prove that

ix cos θ

∞



n=−∞

inθ

(x).