Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

26.3 Second Solution of the Legendre DE 617

and

2n+1

(x)=(−1)

(2n +1)!

(n!)

xF (−n, n +

;

; x

). (26.26)

Historical Notes

Adrien-Marie Legendre came from a well-to-do Parisian family and received an

excellent education in science and mathematics. His university work was advanced

enough that his mentor used many of Legendre’s essays in a treatise on mechanics.

A man of modest fortune until the revolution, Legendre was able to devote himself

to study and research without recourse to an academic position. In 1782 he won the

prize of the Berlin Academy for calculating the trajectories of cannonballs taking

air resistance into account. This essay brought him to the attention of Lagrange

and helped pave the way to acceptance in French scientiﬁc circles, notably the

Academy of Sciences, to which Legendre submitted numerous papers. In July 1784

he submitted a paper on planetary orbits that contained the now-famous Legendre

polynomials, mentioning that Lagrange had been able to “present a more complete

theory” in a recent paper by using Legendre’s results. In the years that followed,

Legendre concentrated his eﬀorts on number theory, celestial mechanics, and the

theory of elliptic functions. In addition, he was a proliﬁc calculator, producing

large tables of the values of special functions, and he also authored an elementary

textbook that remained in use for many decades. In 1824 Legendre refused to vote

for the government’s candidate for the Institut National. Because of this, his pension

was stopped and he died in poverty and in pain at the age of 80 after several years

of failing health.

Adrien-Marie

Legendre

1752–1833

Legendre produced a large number of useful ideas but did not always develop

them in the most rigorous manner, claiming to hold the priority for an idea if

he had presented merely a reasonable argument for it. Gauss,withwhomhehad

several quarrels over priority, considered rigorous proof the standard of ownership.

To Legendre’s credit, however, he was an enthusiastic supporter of his young rivals

Abel and Jacobi and gave their work considerable attention in his writings.

Legendre also contributed to practical eﬀorts in science and mathematics. He

and two of his contemporaries were assigned in 1787 to a panel conducting geodetic

work in cooperation with the observatories at Paris and Greenwich. Four years

later the same panel members were appointed as the Academy’s commissioners to

undertake the measurements and calculations necessary to determine the length of

the standard meter. Legendre’s seemingly tireless skill at calculating produced large

tables of the values of trigonometric and elliptic functions, logarithms, and solutions

to various special equations.

26.3 Second Solution of the Legendre DE

Recall that any second order linear DE has two bases of solutions. We have

so far found one solution of Legendre DE in the form of the Legendre poly-

nomials. Once we have these solutions, we can obtain a second solution using

Equation (24.6). To conform with Equation (24.6), we need to reexpress the

Legendre DE as

−

1 − x

n(n +1)

1 − x

y =0.

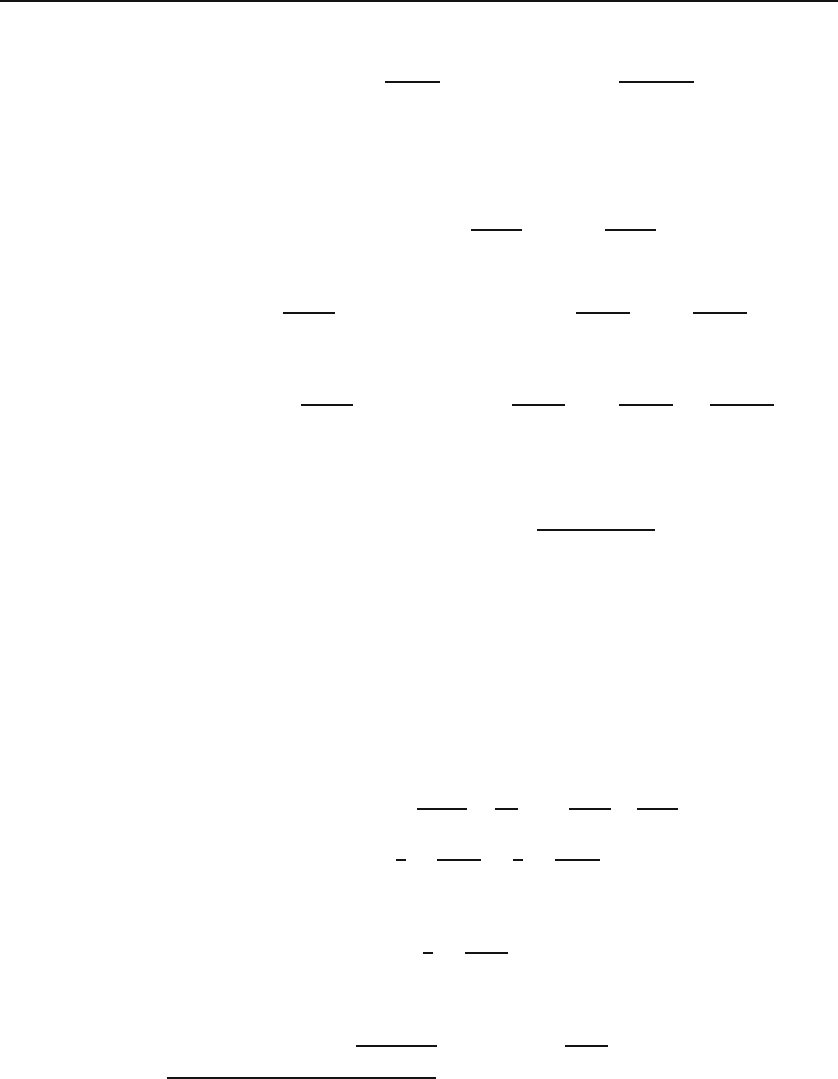
618 Laplace’s Equation: Spherical Coordinates

This is an homogeneous second order linear DE with

p(x)=−

1 − x

and q(x)=

n(n +1)

1 − x

Using P

(x) as our input, we can generate another set of solutions. Let Q

(x)

stand for the linearly independent “partner” of P

(x). Then, setting C =0

in Equation (24.6) yields

(x)=KP

(x)

(s)

exp



1 − t



ds.

But

1 − t

dt = − ln |1 −t



= −ln



1 − s

1 −c



=ln



1 − c

1 − s



so that

exp



1 − t



ds =exp





1 − c

1 − s







1 − c

1 − s



|1 − c

1 − s

because s, being the argument of a Legendre polynomial, is the cosine of an

angle and therefore cannot exceed 1 so that 1 − s

≥ 0. It now follows that

(x)=A

(x)

(1 −s

(s)

, (26.27)

where A

≡ K|1 −c

| is an arbitrary constant determined by convention, and

α is an arbitrary point in the interval [−1, +1]. The subscript for A

indicates

that the constant may be diﬀerent for diﬀerent n. These new solutions are

called Legendre functions of the second kind. Note that, contrary to

Legendre

functions of the

second kind

(x), Q

(x)isnotwellbehavedatx = ±1 due to the presence of 1 − s

in the denominator of the integrand of Equation (26.27). For this reason, we

shall not use these second solutions in this book.

Example 26.3.1.

Example 26.2.2 gives P

(x) = 1. Therefore,

(x)=A

1 − s



1+s

1 − s



= A





1+x

1 − x



−



1+α

1 − α





The standard form of Q

(x) is obtained by setting A

=1andα =0:

(x)=



1+x

1 − x



for |x| < 1.

Similarly, since P

(x)=x,weobtain

(x)=A

(1 − s

= Ax + Bx ln



1+x

1 − x



+ C for |x| < 1,

Since we are interested in a diﬀerent second solution, we can ignore any constant

multiple of the ﬁrst solution that is added to the sought-after second solution.

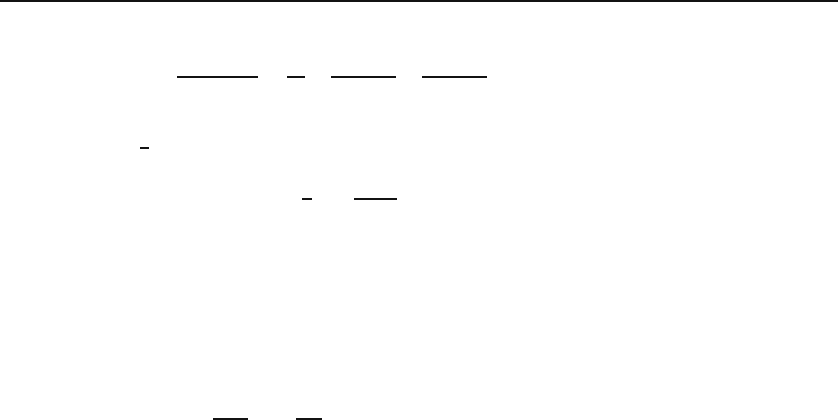
26.4 Complete Solution 619

where A, B,andC are constants, and to perform the integration, we used

(1 − s

2(1 − s)

2(1 + s)

which renders the integral elementary. In the case of Q

(x), convention demands

that A =0,B =

,andC = −1. Thus,

(x)=

x ln



1+x

1 − x



− 1.



26.4 Complete Solution

Having found the angular solution of Laplace’s equation, we now tackle the

radial part. With α = k(k + 1), we can write the ﬁrst equation in (26.2) as

+2r

− k(k +1)R =0. (26.28)

Since p

(0) = 0, we have to consider a solution of the form R(r)=r



∞

n=0

Diﬀerentiating this series and substituting it in Equation (26.28) gives

∞



n=0

[(n + s)(n + s +1)− k(k +1)]b

n+s

[(n + s)(n + s +1)− k(k +1)]b

=0 for n =0, 1, 2,....

In particular, for n = 0, and assuming that b

= 0, we obtain the indicial

equation

an example of the

indicial equation

s(s +1)−k(k +1)=0 ⇒ s = k or s = −k − 1.

For s = k, the equation for general nonzero n gives

[(n + k)(n + k +1)− k(k +1)]b

=0 ⇒ n(n +2k +1)b

=0.

Since neither n nor n +2k + 1 is zero, we have to conclude that b

=0forall

n ≥ 1. Thus, for s = k, we obtain the solution R(r)=A

where A

is an

arbitrary constant (we called it b

before).

For s = −k −1, we have

[(n − k − 1)(n − k) − k(k +1)]b

=0 ⇒ n(n −2k − 1)b

for which we can have either n =2k +1orb

=0. Ifn =2k +1,then

R(r)=r

−k−1

2k+1

= b

2k+1

which is (a constant times) what we already have. So assume that n =2k +1.

Then b

=0foralln ≥ 1, and we obtain the solution R(r)=B

−k−1

where

620 Laplace’s Equation: Spherical Coordinates

is another arbitrary constant. It follows that the most general solution of

the radial DE is

the most general

solution of the

spherical radial DE

(r) ≡ A

k+1

,k=0, 1, 2,....

We can now put the radial and the angular parts together:

Theorem 26.4.1. To ﬁnd the most general azimuthally symmetric solution

of Laplace’s equation in spherical coordinates, we multiply the radial solution

and the angular solution (Legendre polynomial) for each k and sum over all

possible values of k:

Φ(r, θ)=

∞



k=0



k+1



(cos θ), (26.29)

where we have substituted cos θ for u.

Equation (26.29) gives the general solution of Laplace’s equation, and we

From a known

solution of

Laplace’s

equation, we ﬁnd

aformulathat

generates all

Legendre

polynomials.

shall consider examples of how to use it to solve some representative problems,

but ﬁrst we will go backward: From a particular known solution of Laplace’s

equation, we want to ﬁnd an important property of Legendre polynomials.

Equation (15.18) shows that 1/|r − r

| is a solution of Laplace’s equation at

all points of space except r

. In general, |r−r

| is not azimuthally symmetric.

However, if we place r

along the z-axis, the ϕ-dependence will disappear. In

fact, with r

= a

,wehave

|r − r

| = |r − a

| =



+ a

− 2ar cos θ.

According to (26.29) the solution 1/|r − a

| can be written as a series:

√

+ a

− 2ar cos θ

∞



k=0



k+1



(cos θ).

We are interested in the region of space inside the sphere of radius a.Since

the origin is included in this region, no negative powers of r are allowed.

Therefore, all coeﬃcients of such powers must be zero, i.e., B

=0. To

determine the other set of coeﬃcients, evaluate both sides at θ =0anduse

(1) = 1. This gives

√

+ a

− 2ar

|r − a|

a − r

∞



k=0

Using the result of Example 9.3.3 and the fact that r/a < 1, the LHS can be

expanded in powers of r/a:

a −r

a(1 −r/a)

∞



k=0





∞



k=0

k+1

26.4 Complete Solution 621

Comparison of the last two equations gives A

=1/a

k+1

. It follows that

√

+ a

− 2ar cos θ

∞



k=0





(cos θ),r<a.

Introducing t ≡ r/a and u ≡ cos θ on both sides, we ﬁnally obtain the impor-

tant relation

g(t, u) ≡

√

1+t

− 2tu

∞



k=0

(u). (26.30)

The RHS can be considered as a Taylor (or Maclaurin) series in t for the

function on the LHS.

Theorem 26.4.2. The kth coeﬃcient of the Maclaurin series expansion of

g(t, u) ≡ 1/

√

1+t

− 2tu about t =0is P

(u).Speciﬁcally,

(u)=

∂

∂t

√

1+t

− 2tu



t=0

. (26.31)

The function g(t, u) is called the generating function of the Legendre poly-

nomials.

Example 26.4.3.

As an immediate application of the generating function to

potential theory, consider the electrostatic or gravitational potential which can be

written as

Φ(r)=K

dQ(r



)

|r − r



, (26.32)

where K is k

for electrostatics and −G for gravity, and Q represents either electric

charge or mass. Assuming that r  r



, we can expand in powers of the ratio r



which we denote by t. The key to this expansion is the following power series of

1/|r − r



Legendre

polynomial and

multipole

expansion

|r − r



√

+ r

2

− 2r · r





1+t

− 2t cos γ

∞



k=0

(cos γ),

where γ is the angle between r and r



and we used Equation (26.30). Substituting

this expansion for 1/|r − r



| in (26.32), we obtain

Φ(r)=K

∞



k=0

k

k+1

(cos γ) dQ(r



)=K

∞



k=0

k+1

, (26.33)

wherewereplacedt with r



/r and introduced Q

, the so-called k-th moment of

source (charge or mass), by

≡

k

(cos γ) dQ(r



). (26.34)

Do not confuse this Q

with the second solution of Legendre DE introduced in Equation

(26.27).

622 Laplace’s Equation: Spherical Coordinates

Recall that cos γ depends on θ and ϕ. Thus, once the integral over Ω is done, the

result will depend on θ and ϕ as it should, because Φ(r) is, in general, dependent

on these angles.

The moments Q

are supposed to describe the intrinsic properties of charge (or

mass) distributions and should not depend on the observation point—described, in

part, by θ and ϕ. This is the reason that Cartesian coordinates are more useful—at

this level of presentation—than spherical coordinates. In Cartesian coordinates, we

can separate the primed from the unprimed coordinates (as we did in the deﬁnition

of dipole in Chapter 10 and of quadrupole in Chapter 17), and deﬁne multipole

moments entirely in terms of the density function of the distribution of the source.

This does not mean, however, that a complete separation is impossible in spherical

coordinates. In fact, there are techniques of performing such a separation—in terms

of the so-called “spherical harmonics”—but they are much more complicated and

beyond the scope of this book.



26.5 Properties of Legendre Polynomials

From the Legendre DE, the generating function, and other formulas derived

earlier, one can obtain a variety of relations connecting Legendre polynomials.

26.5.1 Parity

The easiest property to obtain is parity which is the content of the following

formula:

(−u)=(−1)

(u). (26.35)

This is a direct consequence of the fact that P

(u) has only even powers of u

if k is even, and odd powers if k is odd.

26.5.2 Recurrence Relation

Diﬀerentiate both sides of Equation (26.30) with respect to t to obtain

u − t

(1 + t

− 2tu)

3/2

∞



k=1

k−1

(u). (26.36)

Rewrite the LHS as

u − t

1+t

− 2tu

√

1+t

− 2tu

u − t

1+t

− 2tu

∞



k=0

(u), (26.37)

where we used (26.30) for the term with the square root. Equating the RHS

of (26.37) with the RHS of (26.36) and multiplying the result by 1 + t

−2tu

yields

(t −u)

∞



k=0

(u)+(1+t

− 2tu)

∞



k=1

k−1

(u)=0

See Hassani, S. Mathematical Physics: A Modern Introduction to Its Foundations,

Springer-Verlag, 1999, Chapter 12 for a discussion of spherical harmonics.

26.5 Properties of Legendre Polynomials 623

∞



k=0

k+1

(u) −u

∞



k=0

(u)+

∞



k=1

k−1

(u)

∞



k=1

k+1

(u) −2u

∞



k=1

(u)=0.

All the coeﬃcients of powers of t must vanish. To ﬁnd these coeﬃcients,

change the dummy index in each sum so that all sums will have the same

power of t.So,letk = n −1 in the ﬁrst and fourth sums, k = n in the second

and the last sums, and k = n + 1 in the third sum. Then the above equation

can be written as

∞



n−1

(u) − uP

(u)+(n +1)P

n+1

(u)

+(n − 1)P

n−1

(u) − 2unP

(u)]t

=0,

where we have purposefully left out the lower limit of summation because

diﬀerent sums start at diﬀerent initial values of n. Since a power series is zero

only if all its coeﬃcients are zero, we set the coeﬃcients of the series above

equal to zero to obtain

recurrence relation

for Legendre

polynomial

(2n +1)uP

(u)=(n +1)P

n+1

(u)+nP

n−1

(u),n=1, 2, 3,.... (26.38)

Using P

(u)=1andP

(u)=u, one can generate all Legendre polynomials

from Equation (26.38).

Example 26.5.1.

For n = 1, Equation (26.38) gives

3uP

(u)=2P

(u)+P

(u) ⇒ 3u

=2P

(u)+1 ⇒ P

(u)=

(3u

− 1)

For n = 2, Equation (26.38) gives

5uP

(u)=3P

(u)+2P

(u) ⇒

u(3u

−1) = 3P

(u)+2u ⇒ P

(u)=

(5u

−3u),

and so on.



The recurrence relation can be used to obtain P

(0) which is a useful

quantity. We quote the result and leave the details as an exercise for the

reader. For odd n,wehaveP

(0) = 0. The result for the even case is

(0) = (−1)

(2n −1)!!

(2n)!!

=(−1)

(2n)!

(n!)

. (26.39)

Example 26.5.2.

We can also obtain P

(0) by letting u = 0 in Equation (26.30):

(1 + t

)

−1/2

∞



k=0

(0).

624 Laplace’s Equation: Spherical Coordinates

The binomial expansion of the LHS gives [see Equation (10.15)]

(1 + t

)

−1/2

=1+

∞



n=1

(−

)(−

− 1) ···(−

− n +1)

=1+

∞



n=1

(−1)

(

+1)···(n −

)

=1+

∞



n=1

(−1)

1 · 3 ···(2n − 1)

Comparing this with the RHS of the ﬁrst equation, we see that P

(0) = 0 when n

is odd and that

(0) = (−1)

1 · 3 ···(2n − 1)

=(−1)

(2n − 1)!!

which is the same as (26.39) because 2

n!=(2n)!! by Problem 11.1.



26.5.3 Orthogonality

The most useful property of the Legendre polynomials is their orthogonality.

We have already seen in Chapters 6 and 7 how dot products can be deﬁned

for polynomials. We now show that Legendre polynomials of diﬀerent orders

are necessarily orthogonal once the dot product is deﬁned in terms of suitable

integrals (also see Example 24.5.3). Write the Legendre DE for P

and P

[(1 −u



(u)] + n(n +1)P

(u)=0,

[(1 −u



(u)] + m(m +1)P

(u)=0,

where the prime indicates derivative. Multiply both sides of the ﬁrst equation

by P

(u) and the second equation by P

(u) and integrate from −1to+1:

−1

[(1−u



(u)]P

(u) du + n(n+1)

−1

(u)P

(u) du =0,

−1

[(1−u



(u)]P

(u) du + m(m+1)

−1

(u)P

(u) du =0. (26.40)

Use integration by parts to write the ﬁrst integral as

−1

[(1 −u



(u)]P

(u) du =(1− u



(u)P

(u)



−1

  

=0 because of (1−u

)

−

−1

[(1 −u



(u)]P



(u) du.

26.5 Properties of Legendre Polynomials 625

The ﬁrst integral of the second line of Equation (26.40) gives exactly the same

result. Therefore, if we subtract the two equations of (26.40), we obtain

[n(n +1)− m(m +1)]

−1

(u)P

(u) du =0.

It now follows that

Theorem 26.5.3. If m = n,then



−1

(u)P

(u) du =0, i.e., if the inner

product is deﬁned as an integral from −1 to +1, then Legendre polynomials of

diﬀerent orders are orthogonal.

We put this orthogonality relation to immediate use. Square both sides

of Equation (26.30) keeping in mind to introduce a new dummy index when

multiplying the sums, and integrate the result from −1to+1:

−1

1+t

− 2tu

−1



∞



k=0

(u)



∞



m=0

(u)



du. (26.41)

On the RHS, we switch the order of summation and integration:

RHS =

∞



k=0

∞



m=0

m+k

−1

(u)P

(u) du



 

=0 unless m=k

As we perform the inner sum, by Theorem 26.5.3, all terms will vanish except

one, i.e., only when m = k. So, the double sum reduces to a single sum

RHS =

∞



k=0

−1

(u) du.

The integral on the LHS of (26.41) can be done by substituting y =1+t

−2tu

and dy = −2tdu:

LHS = −

(1−t)

(1+t)

[ln(1 + t) −ln(1 −t)].

The two natural log terms can be expanded using Equation (10.23). The

reader may check that

[ln(1 + t) −ln(1 −t)] = 2

∞



k=0

2k +1

. (26.42)

The fact that only even powers of t are present could have been anticipated

because the function on the LHS of Equation (26.42) is even in t.Equating

the RHS and the LHS of (26.41), we obtain

∞



k=0

2k +1

∞



k=0

−1

(u) du.

626 Laplace’s Equation: Spherical Coordinates

For these two power series in t to be equal, their coeﬃcients must equal:

−1

(u) du =

2k +1

Combining this with the orthogonality relation of Theorem 26.5.3 and using

the Kronecker delta introduced in Equation (7.9), we have

orthogonality

relation of

Legendre

polynomials

−1

(u)P

(u) du =

2n +1

. (26.43)

26.5.4 Rodrigues Formula

We started our discussion of Legendre polynomials by representing them as

inﬁnite series and then truncating the series due to physical restrictions. We

noted that the recursion relation obtained by the Frobenius method gave all

the coeﬃcients of the polynomials in terms of a

and a

. Later, we found

a “closed” expression for all Legendre polynomials in terms of derivatives of

the generating functions which is a very useful function as the derivation of

(26.43) demonstrated.

There is another “closed” expression of Legendre polynomials which we

shall discuss now. This expression is called the Rodrigues formula and is

given by

Rodrigues formula

(x)=

− 1)

. (26.44)

To see that the RHS indeed gives the nth Legendre polynomial, we show

that it satisﬁes the corresponding Legendre DE. The most elegant way to

show this is to resort to complex analysis where derivatives are represented

as integrals [see Equation (19.10)]. Thus, for f (z)=(z

− 1)

, the Cauchy

integral formula gives

− 1)

2πi

(ξ

− 1)

(ξ − z)

dξ,

and Equations (19.10) and (26.44) yield

(z)=

− 1)

(2πi)

(ξ

− 1)

(ξ − z)

n+1

dξ.

To ﬁnd P



(z)andP



(z), we diﬀerentiate the integral, carrying the derivative

inside and letting it diﬀerentiate the denominator:

(2πi)



(ξ

− 1)

(ξ − z)

n+1



dξ =

n +1

(2πi)

(ξ

− 1)

(ξ − z)

n+2

dξ,





n +1

(2πi)



(ξ

− 1)

(ξ − z)

n+2



dξ

(n +1)(n +2)

(2πi)

(ξ

− 1)

(ξ − z)

n+3

dξ.

Thefactthatweareusingx, rather than u, as the argument of the Legendre polynomial

should not cause any confusion.