Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

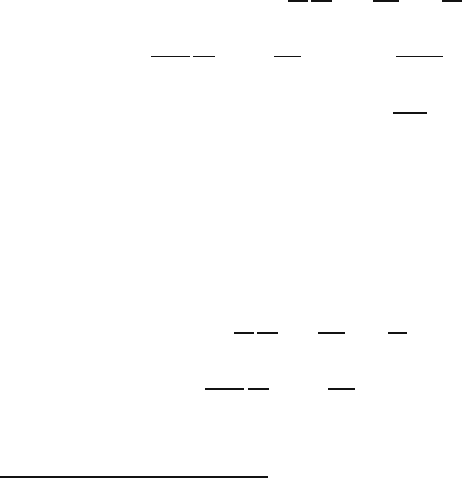
Chapter 26
Laplace’s Equation:
Spherical Coordinates
The separation of Laplace’s equation in spherical coordinates is obtained from
Equation (22.16) by substituting f(r) = 0. This will yield
1
1
r
2
d
dr
r
2
dR
dr
−
α
r
2
R =0,
1
sin θ
d
dθ
sin θ
dΘ
dθ
+
α −
β
sin
2
θ
Θ=0, (26.1)
d
2
S
dϕ
2
+ βS =0.
We consider the case where S is the constant function.
2
This corresponds
to problems with an azimuthal symmetry, i.e., problems for which it is a
azimuthal
symmetry means
independence
from ϕ
priori clear that the potential is independent of the azimuthal angle ϕ.For
such situations, the third equation in (26.1) implies that β = 0 because S is a
(nonzero) constant. The independent variables are reduced to two and, with
Φ(r, θ)=R(r)Θ(θ), the remaining ODEs simplify to
1
r
2
d
dr
r
2
dR
dr
−
α
r
2
R =0,
1
sin θ
d
dθ
sin θ
dΘ
dθ
+ αΘ=0. (26.2)
We shall now concentrate on the second equation and come back to the first
after we have found solutions to the second.
1
Here we have changed the symbol of the azimuthal function to S so that Φ(r, θ, ϕ)=
R(r)Θ(θ)S(ϕ).
2
The case in which S is not constant—so that Φ depends on the azimuthal angle—is
more complicated and will not be pursued here. Instead, the interested reader is referred
to Hassani, S. Mathematical Physics: A Modern Introduction to Its Foundations, Springer-
Verlag, 1999, Chapter 12 for details.

608 Laplace’s Equation: Spherical Coordinates
The appearance of sin θdθ (the differential of cos θ) in the denominator
suggests changing the independent variable from θ to u ≡ cos θ. For any
function f(θ), the chain rule gives
3
df
du
=
df
dθ
dθ
du
=
df
dθ
1
du/dθ
= −
1
sin θ
df
dθ
or
df
dθ
= −sin θ
df
du
, (26.3)
which allows us to convert the derivative of a function with respect to u to
the derivative with respect to θ and vice versa.
Introduce a new function P (u) such that P (u) ≡ Θ(θ). Using the chain
rule, substituting in the second equation of (26.2), and writing sin
2
θ =1−u
2
,
the DE becomes
−
1
sin θ
d
dθ
(1 −u
2
)
dP
du
+ αP =0.
The term in the square brackets is a function of u. So, by Equation (26.3),
we can convert the θ-derivative to a u-derivative and obtain
d
du
(1 −u
2
)
dP
du
+ αP =0, (26.4)
which can also be written as
(1 −u
2
)
d
2
P
du
2
− 2u
dP
du
+ αP = 0 (26.5)
or
Legendre
differential
equation
d
2
P
du
2
−
2u
1 − u
2
dP
du
+
α
1 − u
2
P =0. (26.6)
Equation (26.4), or (26.5), or (26.6) is called the Legendre equation.We
shall solve this DE using the so-called Frobenius method or the method of
undetermined coefficients.
26.1 Frobenius Method
The basic assumption of the Frobenius method is that the solution of the DE
can be represented by a power series. This is not a restrictive assumption
because all functions encountered in physical applications can be written as
power series as long as we are interested in their values lying in their interval
of convergence. This interval may be very small or it may cover the entire
real line.
A second order homogeneous linear DE can be written as
p
2
(x)
d
2
y
dx
2
+ p
1
(x)
dy
dx
+ p
0
(x)y =0. (26.7)
3
Note that f can be considered a function of u as well as θ.
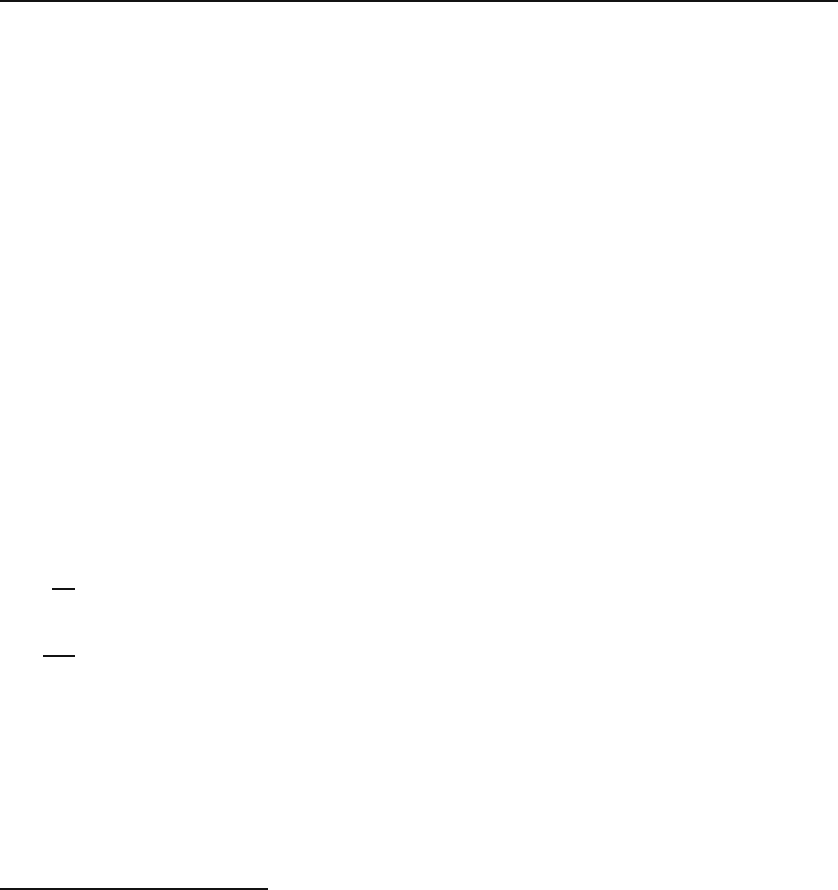
26.1 Frobenius Method 609
For almost all applications encountered in physics (certainly in this book),
p
0
, p
1
,andp
2
are polynomials.
4
The first step in the implementation of the
Frobenius method is to assume an infinite power series for y. It is common
to choose the point of expansion to be x =0. Ifp
2
(0) = 0, only nonnegative
powers of x need be considered.
5
If p
2
(0) = 0, the DE loses its character of
being “second order” and the solutions we are seeking may not be defined
there. In such a case, we have two choices:
1. choose a different point of expansion x
0
=0sothatp
2
(x
0
) =0;or
2. allow nonpositive powers of x in the expansion of y.
The first choice is rarely used. It turns out that the most economic—but
general—way of incorporating the second choice is to write the solution as
y = x
r
∞
n=0
a
n
x
n
=
∞
n=0
a
n
x
n+r
= a
0
x
r
+ a
1
x
r+1
+ a
2
x
r+2
+ a
3
x
r+3
+ ··· ,
(26.8)
where r is a real number (not necessarily a positive integer) to be determined
by the DE.
6
It is customary to choose a
0
= 1 because any constant multiple
of a solution is also a solution; so, if a
0
= 1, we simply multiply the series by
1/a
0
to make it so.
7
Since a power series is uniformly convergent—within its
radius of convergence—it can be differentiated term by term. So, we have
dy
dx
=
∞
n=0
a
n
(n + r)x
n+r−1
= ra
0
x
r−1
+(r +1)a
1
x
r
+ ··· ,
d
2
y
dx
2
=
∞
n=0
a
n
(n + r)(n + r −1)x
n+r−1
(26.9)
= r(r − 1)a
0
x
r−2
+(r +1)ra
1
x
r−1
+(r +2)(r +1)a
2
x
r
+ ··· .
We now substitute Equations (26.8) and (26.9) in the DE (26.7), multiply
out the polynomials into the series, collect all distinct powers of x together,
and set the coefficient of each term equal to zero. We thus obtain a set of
equations whose solution determines r and the a
n
’s. The equation arising form
the lowest power of x involves only r and is called the indicial equation.
indicial equation
This is usually a quadratic equation in r which can be solved to obtain the
4
The DE may not emerge in the form given here out of, say, the separation of variables,
but can be cast in that form. The most complicated form of the coefficients of the derivatives
in a DE are typically rational functions (ratios of two polynomials). Therefore, multiplying
the DE by the product of all three denominators will cast the DE in the form given in
(26.7).
5
For a thorough discussion of the Frobenius method, including motivation and proofs for
the claims cited here, consult Hassani, S. Mathematical Physics: A Modern Introduction
to Its Foundations, Springer-Verlag, 1999, Chapter 14.
6
As Problem 26.2 indicates, one can start with a solution of the form (26.8) even when
p
2
(0) = 0. The differential equation will then force r to be zero.
7
The choice a
0
= 1 is convenient only when p
2
(0) = 0. If p
2
(0) = 0, we need not
restrict a
0
.

610 Laplace’s Equation: Spherical Coordinates
(two) possible values of r, each leading generally to a different solution. The
other equations coming from higher powers of x give recursion relations,
recursion relations
i.e., equations which give a
n
in terms of a
n−1
and a
n−2
. By iterating this
relation, one can obtain all a
n
’s in terms of only two which can be determined
by the BCs. Let us summarize the procedure outlined above:
Theorem 26.1.1. (Frobenius method). To solve the DE (26.7), assume
a solution of the form (26.8). If p
2
(0) =0, choose r =0, substitute y and
its derivatives (26.9) in the DE, multiply out, collect all powers of x,andset
their coefficients equal to zero. If p
2
(0) = 0,leta
0
=1and solve the indicial
equation to obtain r. Set the coefficients of all other powers of x equal to zero
to find the recursion relation giving a
n
in terms of a
n−1
and a
n−2
.Usethis
relation and the values of r obtained above to find all a
n
’s in terms of only
two.
26.2 Legendre Polynomials
We now apply the Frobenius method to the Legendre DE for which—using u
as the independent variable—p
2
(u)=1− u
2
, p
1
(u)=−2u,andp
0
(u)=α.
Since p
2
(0) = 0, we need not introduce an extra power of r for the series.
Therefore, we may write
P (u)=
∞
n=0
a
n
u
n
= a
0
+ a
1
u + a
2
u
2
+ a
3
u
3
+ ··· ,
dP
du
=
∞
n=1
na
n
u
n−1
= a
1
+2a
2
u +3a
3
u
2
+ ···=
∞
n=0
(n +1)a
n+1
u
n
,
d
2
P
du
2
=
∞
n=2
n(n − 1)a
n
u
n−2
=2a
2
+6a
3
u +12a
4
u
2
+ ···
=
∞
n=0
(n +1)(n +2)a
n+2
u
n
.
Multiplying each of the expressions above by its corresponding polynomial,
we obtain
αP (u)=αa
0
+ αa
1
u + αa
2
u
2
+ αa
3
u
3
+ ···=
∞
n=0
αa
n
u
n
,
−2u
dP
du
= −2a
1
u − 4a
2
u
2
− 6a
3
u
3
+ ···= −
∞
n=0
2(n +1)a
n+1
u
n+1
,
(1 −u
2
)
d
2
P
du
2
=2a
2
+6a
3
u +12a
4
u
2
+20a
5
u
3
+ ···
− 2a
2
u
2
− 6a
3
u
3
− 12a
4
u
4
− 20a
5
u
5
+ ···
=2a
2
+6a
3
u +(12a
4
− 2a
2
)u
2
+(20a
5
− 6a
3
)u
3
+ ··· .

26.2 Legendre Polynomials 611
We add these three series, noting that their sum must equal zero
0=αa
0
+ αa
1
u + αa
2
u
2
+ αa
3
u
3
− 2a
1
u − 4a
2
u
2
− 6a
3
u
3
+2a
2
+6a
3
u
+(12a
4
− 2a
2
)u
2
+(20a
5
− 6a
3
)u
3
+ ··· ,
=(αa
0
++2a
2
)+[(α − 2)a
1
+6a
3
]u
+[(α −6)a
2
+12a
4
]u
2
+[(α −12)a
3
+20a
5
]u
3
+ ··· .
The reader may note the pattern emerging in the expression for the coeffi-
cients. In fact, the coefficient of u
n
can be written as [α −n(n +1)]a
n
+(n +
1)(n +2)a
n+2
. Setting this coefficient equal to zero, we obtain the recursion
relation
recursion relation
for the Legendre
equation
a
n+2
=
n(n +1)− α
(n +1)(n +2)
a
n
,n=0, 1, 2,..., (26.10)
which gives all a
n
’s in terms of a
0
and a
1
.
Although writing out the series term by term is a sure way of arriving at
each individual coefficient, and—by the discovery of a pattern—the recursion
relation, manipulation with the summation symbols can also lead to the recur-
sion relations without any expectation of pattern recognition. We go through
How to get to the
recursion relation
(26.10) by
manipulating
summations.
the details of such a manipulation as a noteworthy exercise in working with
the summation signs. The general procedure is to write all sums in such a
way that the exponent of u agrees in all of them. To be specific, we write
all sums over n so that the power of u is n. This may require redefining the
summation index. So, the last term of the DE can be expressed as
αP (u)=
∞
n=0
αa
n
u
n
. (26.11)
Theterminvolvingthefirstderivativeis
−2u
dP
du
= −2u
∞
n=1
na
n
u
n−1
= −
∞
n=1
2na
n
u
n
(26.12)
and the term involving the second derivative becomes
(1 −u
2
)
d
2
P
du
2
=(1−u
2
)
∞
n=2
n(n − 1)a
n
u
n−2
=
∞
n=2
n(n − 1)a
n
u
n−2
−
∞
n=2
n(n −1)a
n
u
n
(26.13)
=
∞
n=0
(n +2)(n +1)a
n+2
u
n
−
∞
n=2
n(n − 1)a
n
u
n
,
where in the first sum we replaced n with n + 2 to change the power of u from
n − 2ton.
8
The power of u in all the sums is now n.
8
Thephrase“inthefirstsum,wereplacedn with n+2” is an abbreviation for a procedure
whereby first a new dummy index m is defined by m = n − 2(orn = m +2),andthenit
is changed back to n.

612 Laplace’s Equation: Spherical Coordinates
The next step is to separate a sufficient number of terms of the “longer
sums” so that all sums start with the same n corresponding to the shortest
sum. In the case at hand, the shortest sum is the one that starts with n =2.
So, rewrite the sums in Equations (26.11), (26.12), and (26.13) as
αP (u)=αa
0
+ αa
1
u +
∞
n=2
αa
n
u
n
,
−2u
dP
du
= −2a
1
u −
∞
n=2
2na
n
u
n
,
(1 −u
2
)
d
2
P
du
2
=2a
2
+6a
3
u +
∞
n=2
(n +2)(n +1)a
n+2
u
n
−
∞
n=2
n(n −1)a
n
u
n
.
Adding these sums and noting that the LHS is zero gives
0=αa
0
+2a
2
+(αa
1
− 2a
1
+6a
3
)u
+
∞
n=2
[αa
n
− 2na
n
+(n +2)(n +1)a
n+2
− n(n − 1)a
n
]
=[α−n(n+1)]a
n
+(n+2)(n+1)a
n+2
u
n
.
By setting the coefficients of all powers of u equal to zero, we obtain
αa
0
+2a
2
=0, (α −2)a
1
+6a
3
=0,
[α −n(n +1)]a
n
+(n +2)(n +1)a
n+2
=0,
with the first two being special cases of the last one, which in turn happens
to be the recursion relation (26.10).
Equation (26.10) is at the heart of the solution to the Legendre DE. It
generates all the a
n
’s with even n from a
0
,andalltheodda
n
’s from a
1
.We
derive a general formula for even a
n
’s, and leave the odd case to the reader.
For n = 0, Equation (26.10) gives a
2
= −(α/2)a
0
,andforn =2weobtain
a
4
=
2 · 3 − α
4 · 3
a
2
=
2 · 3 −α
4 · 3
−
α
2
=
α(α − 2 · 3)
4!
a
0
.
Similarly, for n =4,weget
a
6
=
4 · 5 − α
6 · 5
a
4
= −
α(α − 2 · 3)(α −4 ·5)
6!
a
0
.
The reader may easily check that
a
8
=
α(α − 2 · 3)(α − 4 · 5)(α − 6 · 7)
8!
a
0
.
All these equations show a pattern that can be generalized to
a
2n
=(−1)
n
α(α −2 ·3)(α − 4 · 5) ···[α − (2n − 2)(2n −1)]
(2n)!
a
0
. (26.14)

26.2 Legendre Polynomials 613
Similarly, the odd terms can be calculated with the result
a
2n+1
=(−1)
n
(α −2)(α − 3 · 4)(α −5 · 6) ···[α −(2n −1)2n]
(2n +1)!
a
1
. (26.15)
Inserting these coefficients in the series expansion of P (u), we obtain
P (u)=a
0
∞
n=0
(−1)
n
α(α − 2 · 3)(α − 4 · 5) ···[α − (2n − 2)(2n − 1)]
(2n)!
u
2n
+ a
1
∞
n=0
(−1)
n
(α − 2)(α − 3 · 4)(α −5 ·6) ···[α −(2n −1)2n]
(2n +1)!
u
2n+1
.
(26.16)
If either of the series in Equation (26.16) is to have a physical utility, it
must be convergent. The appearance of (−1)
n
may lead us to believe that
the series is alternating. This is not true, because the terms involving α could
The generalized
ratio test shows
that either of the
series in Equation
(26.16) diverges.
be positive as well as negative. So, we cannot use the alternating series test.
Let us use the ratio test. We apply this ratio test to the even series, the odd
series calculation is identical. Calling the entire nth term of the series c
n
,we
have
lim
n→∞
c
n+1
c
n
= lim
n→∞
a
2n+2
u
2n+2
a
2n
u
2n
= lim
n→∞
2n(2n +1)−α
(2n + 1)(2n +2)
u
2
= u
2
.
So, when u
2
< 1, the series converges. Recall that u =cosθ,andθ =0,π
are points of physical interest corresponding to u = ±1. Therefore, the series
ought to converge there. In this case we cannot decide about the convergence
of the series based on the ratio test. Let us apply the generalized ratio test.
Then, for very large n,wehave
c
n+1
c
n
u
2
=1
=
2n(2n +1)− α
(2n + 1)(2n +2)
=
n
n +1
−
α
(2n + 1)(2n +2)
≈ 1 −
1
n +1
≈ 1 −
1
n
,
and the generalized ratio test implies divergence for the series! This conclusion
holds for both the even and odd series of (26.16).
There is awayofmaking the series convergent. Recall that the parameter
α is completely arbitrary. In particular, we can—if it is helpful—put restric-
To make the series
convergent,
truncate it into a
finite sum!
tions on it. Can we choose α in such a way that the series converges? We
note that as long as the series is infinite, we have no luck because we get back
to the generalized ratio test and divergence. However, if we choose α so that
all a
n
’s after a certain finite number of terms vanish, then the series turns
into a finite sum, and P (u) becomes a polynomial for which the question of
convergence is irrelevant. So, let us assume that a
0
, a
2
, and all the other a’s
up to a
2k
can have nonzero values, but all the remaining coefficients are to

614 Laplace’s Equation: Spherical Coordinates
be zero. All we need to do is to choose α so that a
2k+2
vanishes; then the
recursion relation guarantees the vanishing of a
2k+4
, a
2k+6
,etc.Since
a
2k+2
=
2k(2k +1)− α
(2k + 1)(2k +2)
a
2k
,
we must choose α =2k(2k + 1). A similar argument yields α =(2k − 1)2k
for the odd series.
Choosing α to turn one of the infinite sums into a finite polynomial is only
a partial solution to the problem. Is it possible to choose α so that both the
odd and the even series are truncated after a finite number of terms? Suppose
we have chosen α to be 2k(2k + 1), so that the even series has no term beyond
the (2k)th term. The recursion relation for the odd series can be written as
a
2n+1
=
(2n −1)2n − 2k(2k +1)
(2n +1)2n
a
2n−1
.
Setting the numerator equal to zero gives a quadratic equation which can be
solved for n to obtain
n = −k or n = k +
1
2
.
Neither of these is a positive integer! Thus, the value of α chosen to truncate
the even series does not allow the truncation of the odd series. To avoid
this dilemma, we resort to a choice of another arbitrary constant, a
1
.By
setting a
1
equal to zero, we completely avoid the odd series. Conversely, if
α =(2k − 1)2k—chosen to truncate the odd series—then a
0
ought to be set
equal to zero. By convention, a
0
and a
1
are determined so that P (1) = 1. Let
us summarize our findings:
Theorem 26.2.1. A solution to the Legendre DE (26.5) exists only if α =
k(k +1) where k is a nonnegative integer. The corresponding solution is
denoted by P
k
(u) and is a polynomial of degree k, called the kth Legendre
polynomial, which has only even powers of u if k is even and odd powers of
u if k is odd. By convention P
k
(1) = 1 for all k.
Thus, for each k we have a different solution, and a different a
0
or a
1
to
evaluate. That is why it is more appropriate to write C
k
for either a
0
or a
1
.
We can use either (26.14) and (26.15), or the recursion relation (26.10) to find
the coefficients of each polynomial.
Example 26.2.2.
We calculate the Legendre polynomials up to order 4 using thecalculation of the
first five Legendre
polynomials using
the recursion
relation
recursion relation. P
0
is of degree zero, so it is a constant and P
k
(1) = 1 forces it
to be 1. So, P
0
(u) = 1. Since, P
1
(u) is of degree 1 with no even “powers” of u,it
can be only of the form C
1
u where C
1
is a constant. But P
1
(1) = 1; so C
1
=1and
P
1
(u)=u.ForP
2
, α =2·3 = 6, and the recursion relation gives
a
2
= −
α
2
a
0
= −3C
2
⇒ P
2
(u)=C
2
− 3C
2
u
2
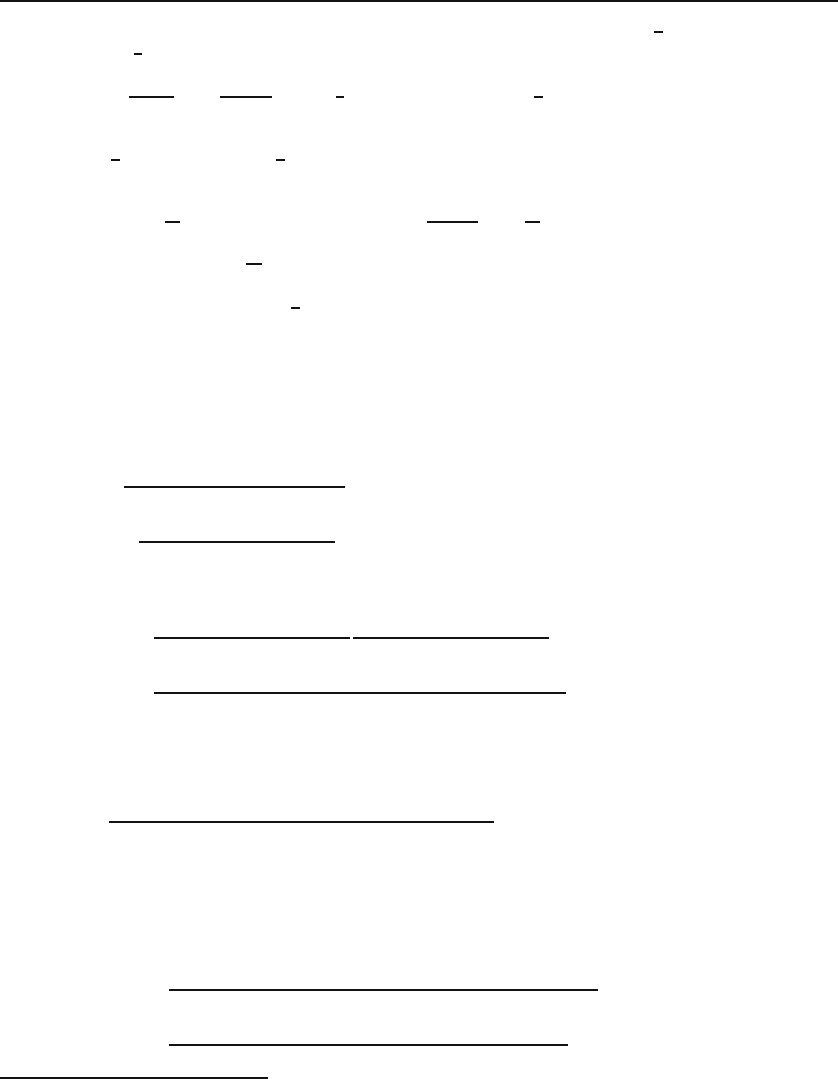
26.2 Legendre Polynomials 615
because P
2
(u)hasnou term. For P
2
(1) to be equal to 1, we must have C
2
= −
1
2
,
so that P
2
(u)=
1
2
(3u
2
−1). For P
3
, α =3· 4 = 12, and the recursion relation gives
a
3
=
2 − α
6
a
1
=
2 − 12
6
C
3
= −
5
3
C
3
⇒ P
3
(u)=C
3
u −
5
3
C
3
u
3
because P
3
(u) has no constant or u
2
term. For P
3
(1) to be equal to 1, we must
have C
3
= −
3
2
,sothatP
3
(u)=
1
2
(5u
3
− 3u). Finally, we calculate P
4
for which
α =4·5 = 20, and the recursion relations give
a
2
= −
20
2
a
0
= −10C
4
and a
4
=
6 − 20
12
a
2
=
35
3
C
4
and P
4
(u)=C
4
− 10C
4
u
2
−
35
3
C
4
u
4
. The condition P
4
(1) = 1 gives C
4
=3/8.
Therefore,
P
4
(u)=
1
8
(35u
4
− 30u
2
+3).
Other Legendre polynomials can be obtained similarly. However, as we shall see
shortly, there is a much easier way of calculating Legendre polynomials.
With α determined to be of the form k(k + 1), we can now calculate all
coefficients of the Legendre polynomials. We start by rewriting the recursion
relation (26.10) as
a
n
=
(n − 2)(n −1) − k(k +1)
n(n − 1)
a
n−2
= −
(k − n +2)(k + n − 1)
n(n − 1)
a
n−2
,n=2, 3,...,k. (26.17)
Iterating this once, we obtain
a
n
=(−1)
2
(k − n +2)(k + n − 1)
n(n − 1)
(k − n +4)(k + n − 3)
(n −2)(n − 3)
a
n−4
=(−1)
2
[(k − n +2)(k − n + 4)][(k + n − 1)(k + n − 3)]
n(n − 1)(n −2)(n − 3)
a
n−4
.
By iterating a few times, the reader may check that
a
n
=(−1)
m
[(k − n +2)(k − n +4)···(k −n +2m)]
·
[(k + n − 1)(k + n −3) ···(k + n − 2m +1)]
n(n −1) ···(n −2m +1)
a
n−2m
. (26.18)
To proceed, we need to take the two cases of even and odd n separately.
We treat the even case and leave the odd case as an exercise for the reader.
Let us assume that n =2m,thenk must also be even
9
and the last equation
above yields
a
2m
=(−1)
m
[(2j) ···(2j − 2m + 2)][(2j +2m −1) ···(2j +1)]
2m(2m −1) ···1
a
0
=(−1)
m
[(2j)!!/(2j −2m)!!][(2j +2m − 1)!!/(2j − 1)!!]
(2m)!
a
0
,
9
Recall from our discussion above that even Legendre polynomials correspond to even
α =2j(2j +1).

616 Laplace’s Equation: Spherical Coordinates
wherewesetk =2j. Using the relations (see Problem 11.1)
(2l −1)!! =
(2l)!
2
l
l!
, (2l)!! = 2
l
l!,
we finally obtain
a
2m
=
(−1)
m
j!
2
j
(2j +2m)!
(j + m)!(j − m)!
1
(2m)!
a
0
≡ A
j
(−1)
m
(2j +2m)!
(j + m)!(j − m)!
1
(2m)!
, (26.19)
where A
j
= a
0
(j!/2
j
). The reader may check that
a
2m+1
= B
j
(−1)
m
(2j +2m +2)!
(j + m +1)!(j − m)!
1
(2m +1)!
(26.20)
for some constant B
j
. Therefore, the even Legendre polynomials will be giveneven Legendre
polynomial
by
P
2j
(x)=A
j
j
m=0
(−1)
m
(2j +2m)!
(j + m)!(j − m)!
x
2m
(2m)!
(26.21)
and the odd polynomials by
odd Legendre
polynomial
P
2j+1
(x)=B
j
j
m=0
(−1)
m
(2j +2m +2)!
(j + m +1)!(j − m)!
x
2m+1
(2m +1)!
. (26.22)
We now introduce a new summation index r = j − m in either sum and let
n =2j in the even sum and n =2j + 1 in the odd sum. Then both sums can
be written simply as
P
n
(x)=K
n
[n/2]
r=0
(−1)
r
(2n −2r)!
(n −r)!r!
x
n−2r
(n − 2r)!
, (26.23)
where [a]—for any real number a—denotes the largest integer less than or
equal to a,andK
n
is an arbitrary constant which, by convention, is taken to
be 1/2
n
so that P
n
(1) = 1. This leads to
P
n
(x)=
1
2
n
[n/2]
r=0
(−1)
r
(2n −2r)!
(n −r)!r!
x
n−2r
(n −2r)!
. (26.24)
Referring to the definition of the hypergeometric function (11.23) and
Equation (26.24), the reader may verify that
P
2n
(x)=(−1)
n
(2n)!
2
2n
(n!)
2
F (−n, n +
1
2
;
1
2
; x
2
) (26.25)
