Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

576 Second-Order Linear Diﬀerential Equations

24.6.1 The Homogeneous Case

The solution to the HNOLDE

L[y] ≡ y

(n)

+ a

n−1

(n−1)

+ ···+ a



+ a

y = 0 (24.27)

can be found by making the exponential substitution y = e

λx

,whichresultsin

characteristic

polynomial of a

HNOLDE

the equation L[e

λx

]=(λ

+ a

n−1

+ ···+ a

λ + a

λx

= 0.This equation

will hold only if λ is a root of the characteristic polynomial

p(λ) ≡ λ

+ a

n−1

+ ···+ a

λ + a

which, by the fundamental theorem of algebra, can be written as

p(λ)=(λ − λ

)

(λ − λ

)

...(λ − λ

)

. (24.28)

The λ

are the distinct roots of p(λ)withλ

having multiplicity k

It is convenient to introduce D ≡ d/dx and deﬁne the diﬀerential

operator

L = p(D)=D

+ a

n−1

+ ···+ a

D + a

Since D − μ and D − λ commute for arbitrary constants μ and λ,wecan

unambiguously factor out the above and obtain

L = p(D)=(D − λ

)

(D − λ

)

...(D − λ

)

. (24.29)

In preparation for ﬁnding the most general solution for Equation (24.27),

we ﬁrst note that

(D − λ)e

λx

− λe

λx

= 0 (24.30)

and

(D − λ)(x

λx

) −λx

λx

= rx

r−1

λx

If we apply D −λ twice, we get

(D − λ)

λx

)=(D − λ)(rx

r−1

λx

)=r(r − 1)x

r−2

λx

and in general,

(D − λ)

λx

)=r(r − 1) ...(r −k +1)x

r−k

λx

which, for k = r,gives

(D −λ)

λx

)=r!e

λx

If we apply D −λ one more time, we get zero by (24.30). Therefore,

(D −λ)

λx

)=0 if k>r. (24.31)

The set of functions

}

−1

, {x

}

−1

, ..., {x

}

−1

24.6 SOLDEs with Constant Coeﬃcients 577

are all solutions of Equation (24.27). For example, an element of the ﬁrst set

yields

L[x

]=(D − λ

)

(D −λ

)

...(D −λ

)

=(D −λ

)

...(D − λ

)

(D − λ

)



 

=0 because k

=0.

If the root λ is complex and the coeﬃcients of the DE are real, then

the complex conjugate λ

∗

is also a root (see Problem 24.14). It follows that

whenever x

is a solution of the DE for complex λ

,soisx

∗

.Thus,

writing λ

= α

+ iβ

and using the linearity of L, we conclude that

cos β

x and x

sin β

x, where r

=0, 1,...,k

− 1,

are all solutions of (24.27).

It is easily proved that the functions x

are linearly independent (see

Problem 24.13). Furthermore,



j=1

= n by Equation (24.28). Therefore,

the set

, where r

=0, 1 ...,k

− 1andj =1, 2,...,m,

contains exactly n elements. We have thus shown that there are at least n

linearly independent solutions for the HNOLDE of Equation (24.27). In fact,

it can be shown that there are exactly n linearly independent solutions.

Box 24.6.1. Let λ

,λ

,...,λ

be the roots of the characteristic poly-

nomial of the real HNOLDE of Equation (24.27), and let the respective

roots have multiplicities k

,...,k

. Then the functions x

,where

=0, 1 ...,k

− 1, are a basis of solutions of Equation (24.27).

Example 24.6.1. An equation that is used in both mechanics and circuit theory is

+ a

+ by =0 with a, b > 0. (24.32)

Its characteristic polynomial is p(λ)=λ

+ aλ + b which has the roots

(−a +



− 4b)andλ

(−a −



− 4b).

We can distinguish three diﬀerent possible motions depending on the relative sizes

of a and b.

(a) a

> 4b (overdamped): Here we have two distinct simple roots. The multi- overdamped

plicities are both one: k

= k

= 1 (see Box 24.6.1). Therefore, the power of t for

both solutions is zero (r

= r

=0). Letγ ≡

√

− 4b. Then the most general

solution is

y(t)=e

−at/2

γt

+ c

−γt

578 Second-Order Linear Diﬀerential Equations

Since a>2γ, this solution starts at y = c

+ c

at t = 0 and continuously

decreases; so, as t →∞, y(t) → 0.

(b) a

=4b (critically damped): In this case we have one multiple root of ordercritically damped

2(k

= 2); therefore, the power of x can be zero or 1 (r

=0, 1). Thus, the general

solution is

y(t)=c

−at/2

+ c

−at/2

This solution starts at y(0) = c

at t = 0, reaches a maximum (or minimum) at

t =2/a − c

, and subsequently approaches zero asymptotically (see Problem

24.23).

< 4b (underdamped): Once more, we have two distinct simple roots. Theunderdamped

multiplicities are both one (k

= k

= 1); therefore, the power of x for both solutions

is zero (r

= r

=0). Letω ≡

√

4b − a

.Thenλ

= −a/2+iω and λ

= λ

∗

.The

roots are complex, and the most general solution is thus of the form

y(t)=e

−at/2

cos ωt + c

sin ωt)=Ae

−at/2

cos(ωt + α).

The solution is a harmonic variation with a decaying amplitude A exp(−at/2). Note

that if a = 0, the amplitude does not decay. That is why a is called the damping

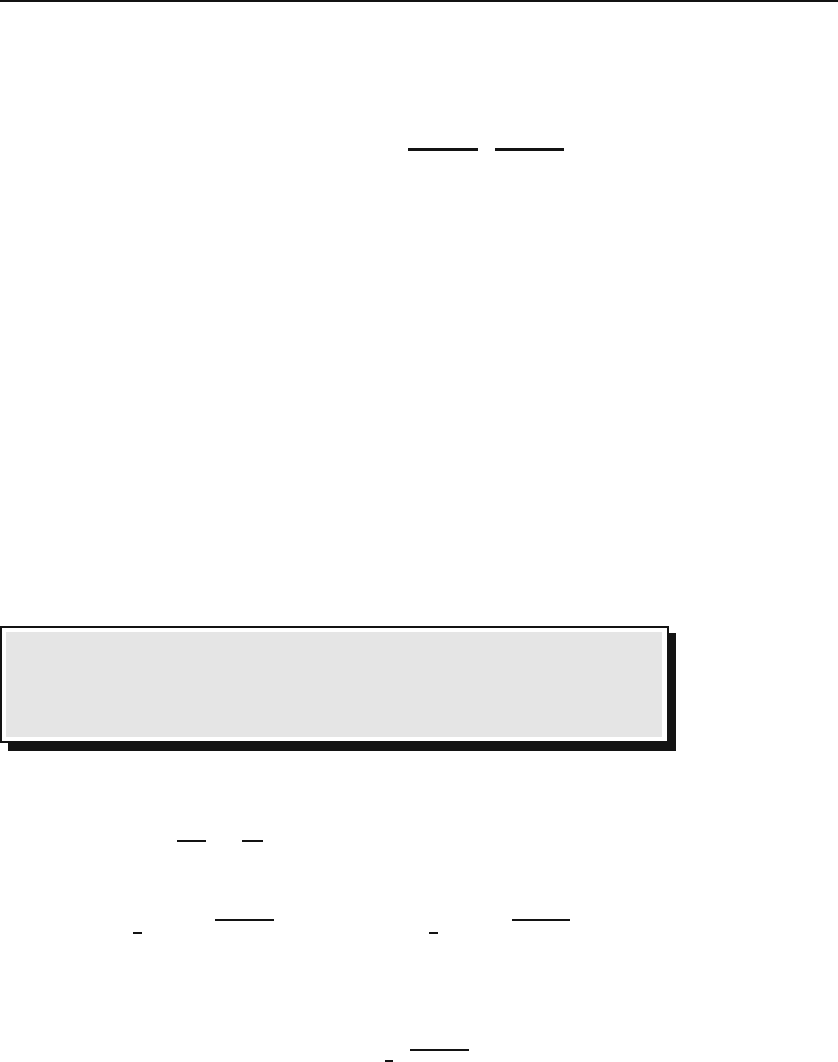
factor (or the damping constant). All three cases are shown in Figure 24.1.damping factor

These equations describe either a mechanical system oscillating (with no external

driving force) in a viscous (dissipative) ﬂuid, or an electrical circuit consisting of a

resistance R, an inductance L, and a capacitance C. For mechanical oscillators,

a = β/m and b = k/m,whereβ is the dissipative constant related to the drag force

drag

and the velocity v by f

drag

= βv,andk is the spring constant (a measure of

the stiﬀness of the spring).

For RLC circuits, a = R/L and b =1/LC. Thus, the damping factor depends

on the relative magnitudes of R and L. On the other hand, the frequency

ω ≡



b −







−

depends on all three elements. In particular, for R ≥ 2



L/C, the circuit does not

oscillate.



Figure 24.1: The solid thin curve shows the behavior of an overdamped oscillator. The

critically damped case is the dashed curve, and the underdamped oscillator is the thick

curve.

24.6 SOLDEs with Constant Coeﬃcients 579

24.6.2 Central Force Problem

One of the nicest applications of the theory of DEs, and the one that initiated central force

problem

the modern mathematical analysis, is the study of motion of a particle under

the inﬂuence of a central gravitational force. Surprisingly, such a motion can

be reduced to a one-dimensional problem, and eventually to a SOLDE with

constant coeﬃcients as follows.

Subsection 12.2.1 treated the equations of motion of a particle under the

inﬂuence of a central force. Conservation of angular momentum and the right

choice of the initial position and velocity (what amounted to setting L =

= L

) eliminated the polar angle θ by assigning it the value π/2. Thus

the particle is conﬁned to the plane perpendicular to the angular momentum

vector, i.e., essentially the vector r × v. The set of three complicated DEs

(12.20) reduces to a much simpler set consisting of (12.22) and (12.24) which

werewritehereas

m¨r −

= F (r), ˙ϕ =

. (24.33)

In principle, we can solve the ﬁrst equation and ﬁnd r as a function of t,

then substitute it in the second equation and integrate the result to ﬁnd ϕ as

a function of time. However, it is more desirable to ﬁnd r as a function of ϕ,

i.e., ﬁnd the shape of the orbit of the moving particle.

In that spirit, we deﬁne a new dependent variable u =1/r, and making

multiple use of the chain rule, we write the DEs with u as the dependent

variable and ϕ as the independent variable. We thus have

r =

⇒ ˙r = −

˙u

= −

˙ϕ

dϕ

= −r

˙ϕ

dϕ

= −

dϕ

¨r = −



dϕ



= −

dϕ

˙ϕ = −

dϕ

= −

dϕ

Substituting for ¨r and r in terms of u and its derivative, Equation (24.33)

yields

dϕ

+ u = −





. (24.34)

Historical Notes

Johannes Kepler (1571–1630) was a premature baby and a very delicate child

who was brought up by his grandparents. After elementary and secondary schooling,

Kepler entered T¨ubingen University to become a Protestant minister. At T¨ubingen

Kepler was taught astronomy by one of the leading astronomers of the day, Michael

Maestlin (1550–1631). The astronomy of the curriculum was, of course, geocen-

tric astronomy. At the end of his ﬁrst year Kepler got ’A’s for everything except

mathematics. Probably Maestlin was trying to tell him he could do better, because

Johannes Kepler

1571–1629

Kepler was in fact one of the select pupils to whom he chose to teach more ad-

vanced astronomy by introducing them to the new, heliocentric cosmological system

580 Second-Order Linear Diﬀerential Equations

of Copernicus. It was from Maestlin that Kepler learned that the preface to Coper-

nicus’s book, explaining that this was ’only mathematics’, was not by Copernicus.

Kepler seems to have accepted almost instantly that the Copernican system was

physically true, and from then on, astronomy and mathematics became his passion.

Kepler also worked and wrote a book in optics, in which he used the idea of a ‘ray

of light’ for the ﬁrst time.

For the Kepler problem this equation is easy to solve because

Kepler problem

F (r)=−

⇒ F





= −Ku

and we have

dϕ

+ u =

. (24.35)

Let v = u − Km/L

. Then Equation (24.35) becomes

dϕ

+ v =0.

The characteristic polynomial of this equation is λ

+ 1, whose roots are

λ = ±i. These simple roots give rise to the linearly independent solutions

v =sinϕ and v =cosϕ. The general solution can therefore be expressed

as v = C

cos ϕ + C

sin ϕ which, using Problem 24.22, can be rewritten as

v = A cos(ϕ −ϕ

). Therefore,

v = u −Km/L

= A cos(ϕ − ϕ

) ⇒ u = Km/L

+ A cos(ϕ −ϕ

)

equation of the

orbits in the

Kepler problem

r =

(Km/L

)+A cos(ϕ − ϕ

)

. (24.36)

This is the equation of a conic section in plane polar coordinates (see Problem

24.15).

We now investigate the details of Equation (24.36). First we note that

when ϕ = ϕ

, r is either a maximum or a minimum depending on the sign

of A. With an ellipse in mind, this corresponds to the (major) axis of the

ellipse making an angle ϕ

with the x-axis. Thus setting ϕ

= 0 corresponds

to choosing the axis of the conic section to be our x-axis. We adhere to this

choice and write

r =

(Km/L

)+A cos ϕ

. (24.37)

Next we want to determine the constant A in terms of the energy of the

particle. The potential energy (PE) is clearly −K/r. So, let us concentrate

Although the Kepler problem usually refers to the gravitational central force, we want

to keep the discussion general enough so that electrostatic force is also included. Thus, K

introduced below can be either GMm or −k

24.6 SOLDEs with Constant Coeﬃcients 581

on the kinetic energy (KE). The velocity of the particle is given in Equation

(12.16) with θ = π/2and

θ =0. Thus

KE =

m(˙r

+ r

˙ϕ

m ˙r

2mr

, (24.38)

where we used the second equation in (24.33). The second term in (24.38) is

sometimes called the centrifugal potential because (like a potential energy)

centrifugal

potential

it is a position-dependent energy that (like a centrifugal force) has resulted

from a velocity-dependent term. Diﬀerentiating Equation (24.37) with respect

to time gives

˙r =

A ˙ϕ sin ϕ

[(Km/L

)+A cos ϕ]

= Ar

˙ϕ sin ϕ.

Squaring and using the second equation in (24.33), we obtain

˙r

= A

˙ϕ

sin

ϕ =

sin

ϕ.

We can eliminate the sine term in favor of terms involving r by solving for

A cos ϕ in (24.37):

A cos ϕ =

−

⇒ A

sin

ϕ = A

−



−



It follows that

KE =

−



−



2mr

−

and

E = KE + PE =

−

so that

A = ±



2mE

To avoid negative signs at later stages, we choose the negative sign now and

ﬁnally write

r =

/(Km)

1 −



2EL

/(K

m)+1 cosϕ

/(Km)

1 − e cos ϕ

, (24.39)

where

e ≡



2EL

+ 1 (24.40)

is called the eccentricity of the conic section.

eccentricity of

orbits

582 Second-Order Linear Diﬀerential Equations

The eccentricity, which by its very deﬁnition is always positive, determines

the shape of the orbit. Let us concentrate on the interesting case of elliptic

orbits corresponding to 0 <e<1 indicating that the total energy of the

particle is negative. Inspection of Problem 24.15 reveals that the semi-major

and semi-minor axes of the ellipse are, respectively,

(1 −e

)

and b

(1 −e

Substituting for e from Equation (24.40) and noting that E<0, we obtain

a = −

⇒ E = −

and b =

√

−2mE

⇒ L =



(24.41)

The negativity of energy in an elliptic orbit is an indication of the stability

of the orbit. The potential energy is negative and larger in absolute value than

the kinetic energy. If the total energy is negative (and, of course, constant),

the particle cannot move too far away from the center of attraction, because

the magnitude of the PE may become too small to oﬀset the positive KE. The

absolute value of this total negative energy is called the binding energy.For

binding energy

an ellipse this binding energy is K/2a.

Kepler’s Laws

In 1609 Johannes Kepler, the German astronomer, after painstakingly an-

alyzing the motion of Mars for many years announced what is now called

Kepler’s ﬁrst law of planetary motion: The orbit of Mars is not a circle

Kepler’s ﬁrst law

but an ellipse. In the context of a very resilient tradition—dating back to

Pythagoras himself—in which circular orbits were given almost a divine sta-

tus, this announcement was truly monumental. Kepler had a hunch that all

planets obey this same law, but could not prove it. Equation (24.37) is the

mathematical statement of Kepler’s ﬁrst law.

Kepler’s second law of planetary motion states that equal areas are

Kepler’s second

law

swept out in equal times by the line joining the planet to the center of attraction

(the Sun). In other words the rate of change of the area is a constant. This

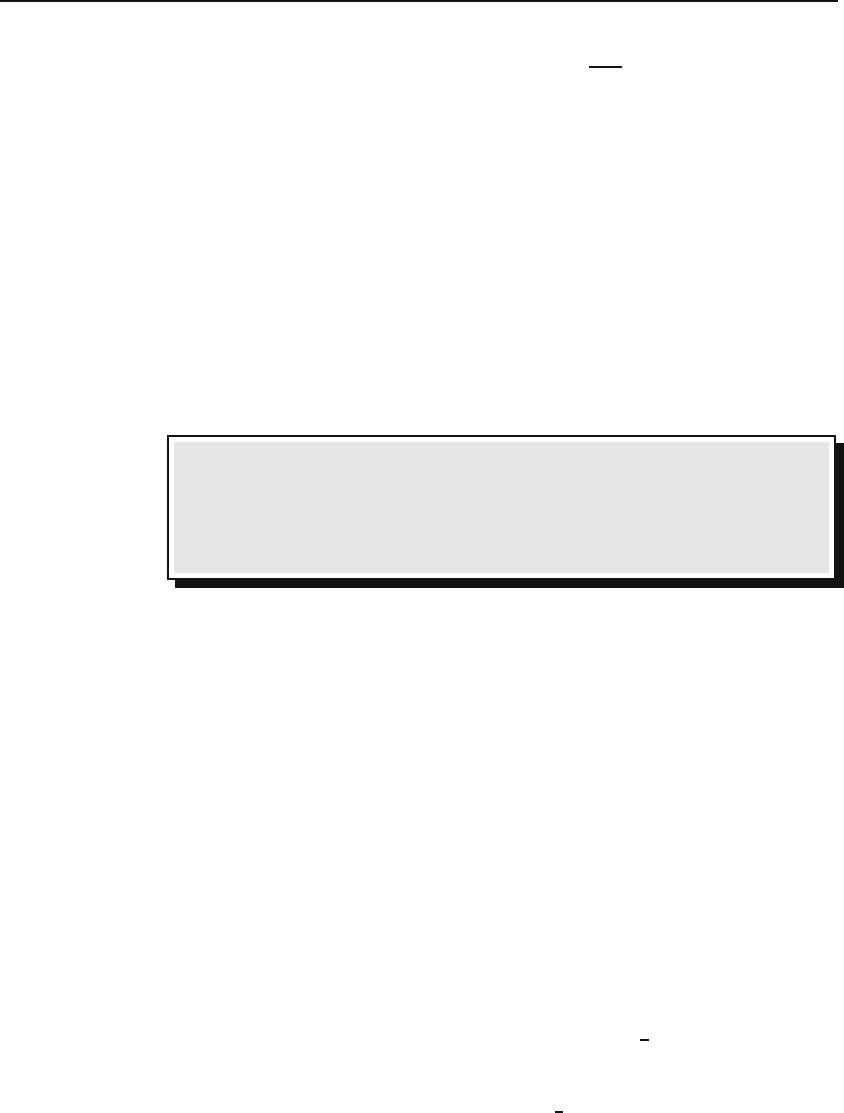
can be seen by referring to Figure 24.2 and noting that

ΔA ≈

rAB ≈

r(rΔϕ) ⇒

ΔA

Δt

≈

Δϕ

Δt

→

˙ϕ.

So, by the second equation in (24.33), dA/dt = L/2m which is a constant.

After the ﬁrst two laws, Kepler spent another 12 years searching for a

“harmony” in the motion of planets. The imperfection he injected in the

planetary motions by the assumption of elliptical orbits prompted him to

seek for some sort of compensation. His third law was precisely that. He felt

that this law, with its precise mathematical structure, gave suﬃcient harmony

to the waltz of planets around the Sun to oﬀset the imperfection of elliptical

24.6 SOLDEs with Constant Coeﬃcients 583

Figure 24.2: The shaded area is almost equal to the area of the triangle SAB.

orbits. Kepler’s third law of planetary motion relates the period of each

planet to the length of its major axis. To derive it, we use Kepler’s second

Kepler’s third law

law:

T =

πab

dA/dt

πab

(L/2m)

2πabm



mK/a b

2πa

3/2

1/2

√

where we used Equation (24.41). For gravity, K = GM m, and squaring both

sides of the above equation gives

4π

This is the mathematical statement of Kepler’s third law.

24.6.3 The Inhomogeneous Case

When a driving force acts on a physical system, it will appear as the inho-

mogeneous term of the NOLDE. For the particular, but important, case in

which the inhomogeneous term is a product of polynomials and exponentials,

the solution can be found in closed form. This subsection shows how this is

done.

We assume that the inhomogeneous term in Equation (24.26) is of the

form r(x)=



(x)e

where p

(x) are polynomials and λ

are (complex)

constants. The most general solution of Equation (24.26) is a linear combi-

nation of a basis of solutions (as given in Box 24.6.1) of the homogeneous

NOLDE and a particular solution of the NOLDE. We need to ﬁnd the latter.

Because L is a linear operator, it is clear that if y

is a particular solution

of L[y]=r

(x)andy

that of L[y]=r

(x), then y

+ y

is a solution of

L[y]=r

(x)+r

(x). This suggests breaking up the inhomogeneous term into

smaller pieces. Thus, no generality is lost if we restrict r(x)tobep(x)e

λx

where p(x)isapolynomial.

The reader may verify that, for any diﬀerentiable function f,wehave

(D −λ)[e

λx

f(x)] = e

λx



(x), (D −λ)

λx

f(x)] = e

λx



(x),

584 Second-Order Linear Diﬀerential Equations

and, in general,

(D −λ)

λx

f(x)] = e

λx

In particular, if p(x) is a polynomial of degree n,then

(D − λ)

u = e

λx

p(x)

has a solution of the form u = e

λx

q(x), where q(x) is a polynomial of degree

n + k that is the primitive (indeﬁnite integral) of p(x)oforderk [so that the

kth derivative of q(x)isp(x)].

If ν = λ, then the reader may check that

(D − ν)[e

λx

f(x)] = e

λx

[(λ − ν)f(x)+f



(x)]

and, therefore, (D − ν)u = e

λx

p(x) has a solution of the form u = e

λx

q(x),

where q(x) is a polynomial of degree k. Applying the last two equations

repeatedly leads to

particular solution

of nth order linear

Box 24.6.2. The NOLDE L[y]=e

λx

S(x),whereS(x) is a polynomial,

has the particular solution e

λx

q(x),whereq(x) is also a polynomial. The

degree of q(x) equals that of S(x) unless λ = λ

, a root of the characteristic

polynomial of L, in which case the degree of q(x) exceeds that of S(x) by

, the multiplicity of λ

Once we know the form of the particular solution of the NOLDE, we can

ﬁnd the coeﬃcients in the polynomial of the solution by substituting in the

NOLDE and matching the powers on both sides.

Example 24.6.2.

We ﬁnd the most general solutions of two diﬀerential equations

subject to the boundary conditions y(0) = 0 and y



(0) = 1.

(a) The ﬁrst DE we want to consider is



+ y = xe

. (24.42)

The characteristic polynomial is λ

+ 1 whose roots are λ

= i and λ

= −i.Thus,

a basis of solutions is {cos x, sin x}. To ﬁnd the particular solution we note that λ

(the coeﬃcient of x in the exponential part of the inhomogeneous term) is 1, which

is neither of the roots λ

and λ

. Thus, the particular solution is of the form q(x)e

where q(x)=Ax + B is of degree 1 [same degree as that of S(x)=x]. We now

substitute u =(Ax + B)e

in Equation (24.42) to obtain the relation

Axe

+(2A + B)e

+(Ax + B)e

= xe

Matching the coeﬃcients, we have

2A =1 and 2A +2B =0 ⇒ A =

= −B.

Thus, the most general solution is

y = c

cos x + c

sin x +

(x − 1)e

24.6 SOLDEs with Constant Coeﬃcients 585

Imposing the given boundary conditions yields 0 = y(0) = c

−

and 1 = y



(0) = c

Thus,

y =

cos x +sinx +

(x − 1)e

is the unique solution.

(b) The next DE we want to consider is



− y = xe

. (24.43)

Here p(λ)=λ

− 1, and the roots are λ

=1andλ

= −1. A basis of solutions

is {e

−x

}. To ﬁnd a particular solution, we note that S(x)=x and λ =1=λ

Box 24.6.2 then implies that q(x)mustbeofdegree2becauseλ

is a simple root,

i.e., k

= 1. We, therefore, try

q(x)=Ax

+ Bx + C ⇒ u =(Ax

+ Bx + C)e

Taking the derivatives and substituting in Equation (24.43) yields two equations,

4A =1 and A + B =0,

whose solution is A = −B =1/4. Note that C is not determined, because Ce

a solution of the homogeneous DE corresponding to Equation (24.43), so when L is

applied to u, it eliminates the term Ce

. Another way of looking at the situation is

to note that the most general solution to (24.43) is of the form

y = c

+ c

−x

−

x + C)e

The term Ce

could be absorbed in c

. We, therefore, set C = 0, apply the

boundary conditions, and ﬁnd the unique solution

y =

sinh x +

− x)e



The inhomogeneous DE (IDE) L[y]=r(x) can be thought of as a machine

(or a black box) that produces a function y(x) when a function r(x)isfed

into it. Such an interpretation is common in the study of electrical or acoustic

ﬁlters. A signal, the function r(x), is sent into the ﬁlter, and a second function,

y(x), is received as an output. In such a context, by far the most important

input signal is a sinusoidal function of the general form r(t)=A cos(ωt + α),

which, with B = Ae

iα

, can be written in complex notation as (see Example

18.2.3)

r(t)=Re(R(t)) where R(t) ≡ Be

iωt

= Ae

i(ωt+α)

where A, B, α,andω, the angular frequency, are all constants, and t represents

time (the independent variable). Assuming that iω is not a root of p(λ),

the characteristic polynomial of L, Box 24.6.2 suggests a particular (complex)

solution, U = C(ω)e

iωt

where C(ω)isa(ω-dependent) constant. To determine

it, we substitute U in L[U ]=Be

iωt

L[U]=L[C(ω)e

iωt

]=C(ω)L[e

iωt

]=C(ω)p(iω)e

iωt

so that

L[U]=Be

iωt

⇒ C(ω)p(iω)e

iωt

= Be

iωt

⇒ C(ω)=

p(iω)