Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

28.2 The Schr¨odinger Equation 669

Construction of Hermite Polynomials

The fact that we are interested in the behavior of ψ (and therefore, H)asx

(or y) goes to inﬁnity permits us to concentrate on the very large powers of y

in the series for H(y). Hence, separating the even and odd parts of the series,

we may write

H(y)=

∞



k=0

∞



k=0

2k+1

= P

2M+1

(y)+

∞



k=M+1

∞



k=M+1

2k+1

(28.11)

= P

2M+1

(y)+

∞



k=0

2k+2M+2

∞



k=0

2k+2M+3

where P

2M+1

(y) is a generic polynomial obtained by adding all the “small”

powers of the series, and M is a very large number.

Now note that for very

large n, the recursion relation yields

n+2

≈

(n +1)(n +2)

≈

(n)(n)

≈

⇒ c

≈

n − 2

n−2

A few iterations give

≈

(n −2)(n − 4) ···(n −2k)

n−2k

In particular,

2k+N

≈

(2k + N −2)(2k + N −4) ···(N)

. (28.12)

To ﬁnd the coeﬃcients in Equation (28.11), ﬁrst let N =2M + 2 and obtain

2k+2M+2

≈

(2k +2M )(2k +2M −2) ···(2M +2)

2M+2

[2(k + M)][2(k + M −1)] ···[2(M +1)]

2M+2

(28.13)

(k + M)(k + M −1) ···(M +1)

2M+2

(k + M)!

2M+2

Similarly

2k+2M+3

≈

(2M +1)!!

(2k +2M +1)!!

2M+3

[2(M +1)]!/[2

M+1

(M +1)!]

[2(k + M +1)]!/[2

k+M+1

(k + M +1)!]

2M+3

[2(M + 1)]!(k + M +1)!

(M + 1)![2(k + M +1)]!

2M+3

, (28.14)

In particular, M is very large compared to λ of Equation (28.10).

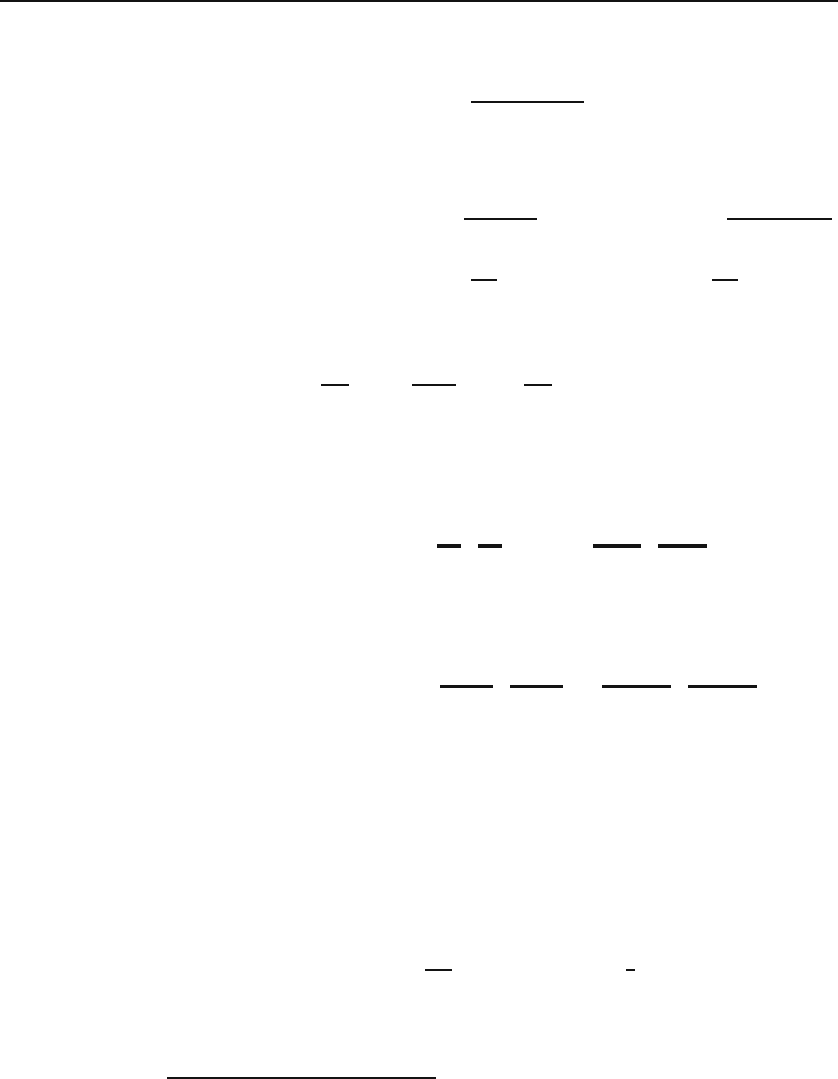
670 Other PDEs of Mathematical Physics

where we used the result of Problem 11.1. By using the Stirling approximation

(11.6), the reader may verify that

2k+2M+3

≈

(M +1)!

(k + M +1)!

2M+3

. (28.15)

With the coeﬃcients given in terms of two constants (c

2M+2

and c

2M+3

Equation (28.11) becomes

H(y)=P

2M+1

(y)+c

2M+2

M!y

∞



k=0

2k+2M

(k + M)!

+ c

2M+3

(M +1)!y

∞



k=0

2k+2M+2

(k + M +1)!

= P

2M+1

(y)+c

2M+2

M!y

∞



j=M

+ c

2M+3

(M +1)!y

∞



j=M+1

. (28.16)

The ﬁrst sum over j can be reexpressed as follows:

∞



j=M

∞



j=0

)

−

M−1



j=0

= e

− Q

2M−2

(y),

where Q

2M−2

(y) is a polynomial of degree 2M − 2iny. The second sum in

(28.16) can be expressed similarly. Adding all the polynomials together, we

ﬁnally get

H(y) ≈ P

2M+1

(y)+c

2M+2



 

≡β

+ c

2M+3

(M +1)!



 

≡α

= P

2M+1

(y)+(α

y + β

. (28.17)

Let us now go back to ψ(y) and note that

ψ(y)=H(y)e

−y

≈ P

2M+1

(y)e

−y

  

→0asy →∞

+(α

y + β

  

→∞ as y →∞

because any exponential decay outweighs any polynomial growth. It follows

that, if H(y) is an inﬁnite series, ψ(y) will diverge at inﬁnity.Fromaphysical

standpoint this means that the quantum particle inside the harmonic oscillator

potential well has an inﬁnite probability of being found at inﬁnity!

To avoid this unrealistic conclusion, we have to reexamine H(y). The caseTruncation of the

inﬁnite series gives

the quantization

of harmonic

oscillator energy

levels.

of Legendre polynomials tells us that the inﬁnite series needs to be truncated.

This will take place only if the numerator of the recursion relation vanishes for

some n, i.e., if λ =2m for some integer m. An immediate consequence of such

a truncation is the famous quantization of the harmonic oscillator energy:

2m = λ =

ω

− 1 ⇒ E =(m +

)ω.

The polynomials obtained by truncating the inﬁnite series are called the

Hermite polynomials. We now construct them. With λ =2m, the recursion

Hermite

polynomials

relation (28.10) can be written as

The Copenhagen interpretation, the only valid interpretation of quantum mechan-

ics, states that |ψ(x)|

is the probability density for ﬁnding the particle at x.

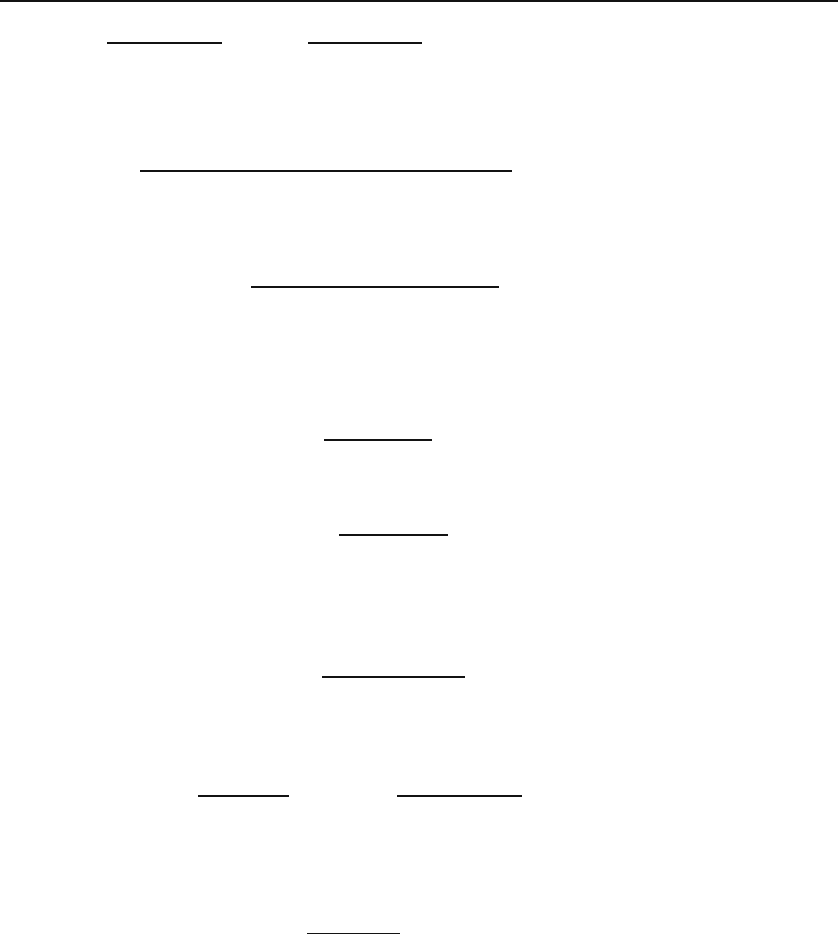
28.2 The Schr¨odinger Equation 671

2(n − m − 2)

n(n − 1)

n−2

= −

2(m +2− n)

n(n −1)

n−2

,m≥ n ≥ 2.

The upper limit for n is due to the truncation mentioned above. After a few

iteration, the pattern will emerge and the reader may verify that

=(−1)

(m +2−n)(m +4− n) ···(m +2k −n)

n(n − 1) ···(n − 2k +1)

n−2k

. (28.18)

We need to consider the two cases of even and odd n separately. For n =2k,

we get

=(−1)

m(m −2) ···(m +2− 2k)

(2k)!

. (28.19)

Now, since the numerator of (28.10) must vanish beyond some integer, and

since 2n =4k,wemusthaveλ =4j or m = λ/2=2j for some integer j.

Then, the reader may check that

=(−1)

(2k)!(j − k)!

(28.20)

and

(y)=c

(j)



k=0

(−1)

(2k)!(j − k)!

, (28.21)

where we have given the constant a superscript to distinguish among the c

’s

of diﬀerent j’s. The odd polynomials can be obtained similarly:

2j+1

(y)=c

(j)



k=0

(−1)

2k+1

(2k +1)!(j − k)!

2k+1

. (28.22)

The constants are determined by convention. To adhere to this convention,

we deﬁne

(j)

(−1)

(2j)!

(j)

(−1)

(2j +1)!

The reader may check that, with these constants, the Hermite polynomials of

all degrees (even or odd) can be concisely written as

(y)=

[n/2]



r=0

(−1)

(n − 2r)!r!

(2y)

n−2r

, (28.23)

where [a], for any real a, stands for the largest integer less than or equal to a.

Orthogonality of Hermite Polynomials

The Hermite polynomials satisfy an orthogonality relation resembling that of

the Legendre polynomials. We can obtain this relation by multiplying the DE

672 Other PDEs of Mathematical Physics

for H

(x)byH

(x)e

−x

,andtheDEforH

(x)byH

(x)e

−x

and subtract-

ing. The factor e

−x

, the so-called weight function, may appear artiﬁcial inweight function

for Hermite

polynomials

this derivation, but an in-depth analysis of the classical orthogonal polyno-

mials, of which Hermite and Legendre polynomials are examples, reveals that

such weight functions are necessary. The reason we did not see such a factor

in Legendre polynomials was that for them, the weight function is unity.

any rate, the result of the above suggested calculation will be



− 2xH



− H



+2xH



−x

+(2m −2n)H

−x

=0.

The reader may easily verify that the ﬁrst term is the derivative of



− H



−x

so that



− H



−x

+(2m − 2n)H

−x

and if we integrate this over the entire real line, we obtain



− H



−x



∞

−∞

+(2m −2n)

∞

−∞

(x)H

(x)e

−x

dx =0.

The ﬁrst term vanishes because of the exponential factor. It now follows that

if m = n,then

orthogonality of

Hermite

polynomials

∞

−∞

(x)H

(x)e

−x

dx =0. (28.24)

Generating Function for Hermite Polynomials

We constructed the generating function for Legendre polynomials in Chapter

26. Here we want to do the same thing for Hermite polynomials. By deﬁnition,

the generating function must have an expansion of the form

g(t, x)=

∞



n=0

(x),

where a

is a constant to be determined. Diﬀerentiate both sides with respect

to x assuming that t is a constant:

∞



n=1



(x).

The sum starts at 1 because H



(x) = 0. Use the result of Problem 28.7 to

obtain

∞



n=1

(2n)H

n−1

(x)=2t

∞



n=1

n−1

(x).

We have no space to go into the details of the theory of classical orthogonal polynomials,

but the interested reader can ﬁnd a uniﬁed discussion of them in Hassani, S. Mathematical

Physics: A Modern Introduction to Its Foundations, Springer-Verlag, 1999, Chapter 7.

28.2 The Schr¨odinger Equation 673

Now choose the constant a

in such a way that it satisﬁes the recursion relation

= a

n−1

. It then follows that

=2t

∞



n=1

n−1

(x)=2t

∞



m=0

(x)=2tg.

Thus

=2tdx ⇒ ln g =2tx +lnC(t) ⇒ g(t, x)=C(t)e

2tx

where the “constant” of integration has been given the possibility of depending

on the other variable, t. To ﬁnd this constant of integration, we ﬁrst determine

n−1

n−2

n(n −1)

= ···=

n−k

n(n − 1) ···(n − k +1)

···=

Using our results obtained so far, we get

C(t)e

2tx

= a

∞



n=0

(x) →

∞



n=0

(x),

where in the last step we absorbed a

(really 1/a

) in the “constant” C(t).

To determine C(t), evaluate both sides of the equation at x =0andusethe

result of Problem 28.8. This yields

C(t)=

∞



n=0

(0) =

∞



k=0

(2k)!

(−1)

(2k)!

∞



k=0

(−t

)

= e

−t

It follows that

2tx−t

∞



n=0

(x). (28.25)

We now summarize what we have done:

generating

function for

Hermite

polynomials

Box 28.2.1. The nth coeﬃcient of the Maclaurin series expansion of the

generating function g(t, x) ≡ e

2tx−t

about t =0is H

(x).Speciﬁcally,

(x)=

∂

∂t

2tx−t



t=0

. (28.26)

We can put the result above to immediate good use. Let us square both

sides of Equation (28.25), multiply by e

−x

, and integrate the result from −∞

674 Other PDEs of Mathematical Physics

to +∞.FortheLHS,wehave

LHS =

+∞

−∞

2(2tx−t

)

−x

dx = e

−2t

+∞

−∞

−x

+4tx

= e

−2t

+∞

−∞

−(x−2t)

+4t

dx = e

+∞

−∞

−(x−2t)

= e

+∞

−∞

−u

du =

√

πe

√

∞



n=0

(2t

)

√

∞



n=0

where we introduced u = x − 2t for the integration variable, and used the

result of Example 3.3.1.

To square the RHS, we need to write it as the product of two inﬁnite sums

using two diﬀerent dummy indices! Therefore,

RHS =

+∞

−∞



∞



n=0

(x)



∞



m=0

(x)



−x

∞



m,n=0

m+n

m!n!

+∞

−∞

(x)H

(x)e

−x



 

=0 unless m = n by (28.24)

∞



n=0

(n!)

+∞

−∞

(x)]

−x

dx.

Comparing the LHS and the RHS, we conclude that

+∞

−∞

(x)]

−x

dx =

√

π 2

n!.

We can combine this result and Equation (28.24) and write

+∞

−∞

(x)H

(x)e

−x

dx =

√

π 2

n!δ

, (28.27)

where δ

is the Kronecker delta which is 1 if m = n and 0 if m = n.

Historical Notes

Charles Hermite, one of the most eminent French mathematicians of the nine-

teenth century, was particularly distinguished for the clean elegance and high artistic

quality of his work. As a student, he courted disaster by neglecting his routine as-

signed work to study the classic masters of mathematics; and though he nearly

failed his examinations, he became a ﬁrst-rate creative mathematician while still in

his early twenties. In 1870 he was appointed to a professorship at the Sorbonne,

where he trained a whole generation of well-known French mathematicians, includ-

ing Picard, Borel,andPoincar´e.

Charles Hermite

1822–1901

The character of his mind is suggested by a remark of Poincar´e: “Talk with

M. Hermite. He never evokes a concrete image, yet you soon perceive that the

28.2 The Schr¨odinger Equation 675

most abstract entities are to him like living creatures.” He disliked geometry, but

was strongly attracted to number theory and analysis, and his favorite subject was

elliptic functions, where these two ﬁelds touch in many remarkable ways. Earlier in

the century the Norwegian genius Abel had proved that the general equation of the

ﬁfth degree cannot be solved by functions involving only rational operations and

root extractions. One of Hermite’s most surprising achievements (in 1858) was to

show that this equation can be solved by elliptic functions.

His 1873 proof of the transcendence of e was another high point of his career.

If he had been willing to dig even deeper into this vein, he could probably have

disposed of π as well, but apparently he had had enough of a good thing. As he

wrote to a friend, “I shall risk nothing on an attempt to prove the transcendence

of the number π. If others undertake this enterprise, no one will be happier than I

at their success, but believe me, my dear friend, it will not fail to cost them some

eﬀorts.” As it turned out, Lindemann’s proof nine years later rested on extending

Hermite’s method.

Several of his purely mathematical discoveries had unexpected applications many

years later to mathematical physics. For example, the Hermitian forms and matrices

that he invented in connection with certain problems of number theory turned out

to be crucial for Heisenberg’s 1925 formulation of quantum mechanics, and Hermite

polynomials are useful in solving Schr¨odinger’s wave equation.

28.2.2 Quantum Particle in a Box

The behavior of an atomic particle of mass μ conﬁned in a rectangular box

with sides a, b,andc (an inﬁnite three-dimensional potential well) is gov-

quantum particle

in a box

erned by the Schr¨odinger equation for a free particle, i.e., V =0. Withthis

assumption, the ﬁrst equation of (28.5) becomes

∇

ψ +

2μE



ψ =0.

A separation of variables, ψ(x, y, z)=X(x)Y (y)Z(z), yields the ODEs:

+ λX =0,

+ σY =0,

+ νX =0,

with λ + σ + ν =2μE/

(see Example 22.2.1).

These equations, together with the boundary conditions

ψ(0,y,z)=ψ(a, y, z)=0 ⇒ X(0) = 0 = X(a),

ψ(x, 0,z)=ψ(x, b, z)=0 ⇒ Y (0) = 0 = Y (b), (28.28)

ψ(x, y, 0) = ψ(x, y, c)=0 ⇒ Z(0) = 0 = Z(c),

Transcendental numbers are those that are not roots of polynomials with integer

coeﬃcients.

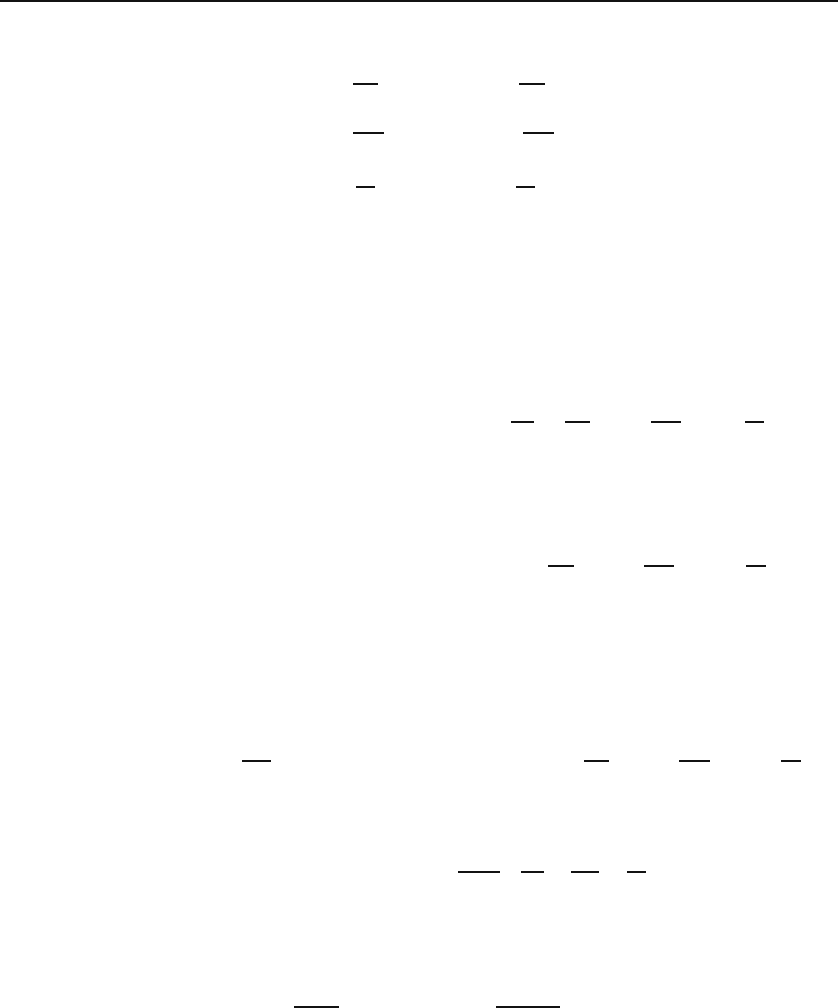
676 Other PDEs of Mathematical Physics

lead to the following solutions:

(x)=sin



nπ



,λ



nπ



for n =1, 2,...,

(y)=sin



mπ



,σ



mπ



for m =1, 2,...,

(z)=sin



lπ



,ν



lπ



for l =1, 2,...,

where the multiplicative constants have been suppressed.

The BCs in Equation (28.28) arise from the demand that the probability

quantum

tunneling

of ﬁnding the particle be continuous and that it be zero outside the box. This

is not true for a particle inside a ﬁnite potential well, in which case the particle

has a nonzero probability of “tunneling” out of the well.

The time equation has a solution of the form

T (t)=e

−iω

lmn

where ω

lmn



2μ



nπ





mπ





lπ



The solution of the Schr¨odinger equation that is consistent with the bound-

ary conditions is, therefore,

ψ(x, y, z, t)=

∞



l,m,n=1

lmn

−iω

lmn

sin



nπ



sin



mπ



sin



lπ



The constants A

lmn

are determined by the initial shape ψ(x, y, z, 0) of the

wave function. In fact, setting t = 0, multiplying by the product of the three

sine functions in the three variables, and integrating over appropriate intervals

for each coordinate, we obtain

lmn

abc

dzψ(x, y, z, 0) sin



nπ



sin



mπ



sin



lπ



The energy of the particle is

E = ω

lmn



2μ





Each set of three positive integers (n, m, l)representsaquantum state of

the particle. For a cube, a = b = c ≡ L, and the energy of the particle is

E =



2μL

+ m

+ l



2μV

2/3

+ m

+ l

), (28.29)

where V = L

is the volume of the box. The ground state is (1, 1, 1), has

energy E =3

/2μV

2/3

, and is nondegenerate (only one state corresponds

to this energy). However, the higher-level states are degenerate. For instance,

28.2 The Schr¨odinger Equation 677

the three distinct states (1, 1, 2), (1, 2, 1), and (2, 1, 1) all correspond to the

same energy, E =6

/2μV

2/3

. The degeneracy increases rapidly with

larger values of n, m,andl.

Equation (28.29) can be written as

+ m

+ l

= R

where R

2μEV

2/3



This looks like the equation of a sphere in the nml-space. If R is large, the

number of states contained within the sphere of radius R (the number of states

with energy less than or equal to E) is simply the volume of the ﬁrst octant

of the sphere. If N is the number of such states, we have

N =



4π





2μEV

2/3





3/2



2μE





3/2

Thus the density of states (the number of states per unit volume) is then

density of states

n =



2μ





3/2

. (28.30)

This is an important formula in solid-state physics, because the energy E is

(with minor modiﬁcations required by spin) the Fermi energy.IftheFermi

Fermi energy

energy is denoted by E

, Equation (28.30) gives E

= αn

2/3

where α is some

constant.

28.2.3 Hydrogen Atom

When an electron moves around a nucleus containing Z protons, the potential

energy of the system is V (r)=−Ze

/r. In units in which  and the mass of

the electron are set equal to unity, the time-independent Schr¨odinger equation

of (28.5) gives

∇

Ψ+



2E +

2Ze



Ψ=0.

The radial part of this equation is given by the ﬁrst equation in (22.16) with

f(r)=2E +2Ze

/r. Deﬁning u = rR(r), we may write



λ +

−



u =0, (28.31)

where λ =2E and a =2Ze

. This equation can be further simpliﬁed by

deﬁning r ≡ kz (k is an arbitrary constant to be determined later):



λk

−



u =0.

This is because n, m,andl are all positive.

678 Other PDEs of Mathematical Physics

Choosing λk

= −

and introducing β ≡ a/(2

√

−λ) yields



−



u =0. (28.32)

Let us examine the two limiting cases of z →∞and z → 0. For the ﬁrst

case, Equation (28.32) reduces to

−

u =0 ⇒ u = e

−z/2

For the second case the dominant term will be α/z

and the DE becomes

−

u =0

for which we try a solution of the form z

with m to be determined by

substitution:

= m(m −1)z

m−2

⇒ m(m − 1)z

m−2

−

=0 ⇒ α = m(m −1).

Recalling from Theorem 26.2.1 that α = l(l + 1), we determine m to be l +1.

Factoring out these two limits, we seek a solution for (28.32) of the form

u(z)=z

l+1

−z/2

f(z).

Substitution of this function in (28.32) gives a new DE:





2(l +1)

− 1





−

l +1− β

f =0. (28.33)

Multiplying by z gives



+[2(l +1)− z]f



− (l +1− β)f =0

which is a conﬂuent hypergeometric DE [see Equation (11.27)]. Therefore, as

the reader may verify, f is proportional to Φ(l +1− β, 2l +2;z). Thus, the

solution of (28.31) can be written as

u(z)=Cz

l+1

−z/2

Φ(l +1−β, 2l +2;z).

Laguerre Polynomials

An argument similar to that used in the discussion of a quantum harmonic

oscillator will reveal that the product e

−z/2

Φ(l+1−β,2l+2;z) will be inﬁnite

unless the power series representing Φ terminates (becomes a polynomial).

This takes place only if (see Box 11.2.2)

l +1− β = −N (28.34)