Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

28.4 Problems 689

(c)

a/2 a

a/4

ψ (x, 0)

(b)

a/2 a

a/4

ψ (x, 0)

(a)

a/2 a

a/4

ψ (x, 0)

− a/4

Figure 28.1: The initial shape of the waves.

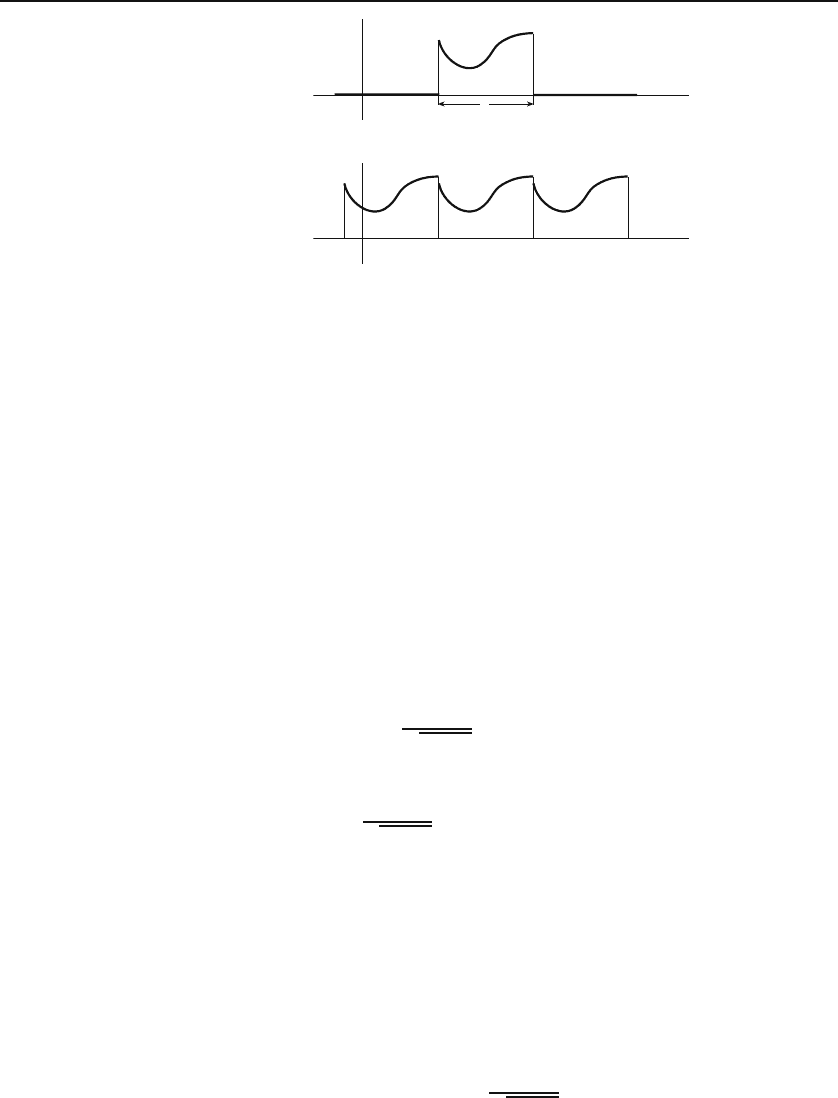
28.13. Repeat Problem 28.12 assuming that the initial displacement is zero

and the initial velocity distribution is given by each ﬁgure.

28.14. Repeat Problem 28.13 assuming that the initial velocity distribution

is given by:

(a) g(x)=

⎧

⎨

⎩

if 0 ≤ x ≤

0if

<x≤ a.

(b) g(x)=

⎧

⎨

⎩

sin

2πx

if 0 ≤ x ≤

0if

<x≤ a.

28.15. A wave guide consists of two coaxial cylinders of radii a and b (b>a).

Find the electric ﬁeld for a TM mode propagating along the two cylinders in

the region between them. Hint: Both linearly independent solutions of the

Bessel DE are needed for the radial function.

Part VII

Special Topics

Chapter 29

Integral Transforms

Chapters 26 and 27 illustrated the Frobenius method of solving diﬀerential

equations using power series, which gives a solution that converges within an

interval of the real line. This chapter introduces another method of solving

DEs, which uses integral transforms. The integral transform of a function

v is another function u given by

u(x)=

K(x, t)v(t) dt, (29.1)

where (a, b) is a convenient interval, and K(x, t), called the kernel of the

kernel of integral

transforms

integral transform, is an appropriate function of two variables.

The idea behind using integral transform is to write the solution u(x)

of a DE in x in terms of an integral such as Equation (29.1) and choose v,

the kernel, and the interval (a, b) in such a way as to render the DE more

Strategy for

solving DEs using

integral transforms

manageable. There are many kernels appropriate for speciﬁc DEs. However,

two kernels are most widely used in physics, which lead to two important

integral transforms, the Fourier transform and the Laplace transform.

29.1 The Fourier Transform

Fourier transform has a kernel of the form K(x, t)=e

itx

andaninterval

(−∞, +∞). Let us see how this comes about.

The Fourier series representation of a function F(x) is valid for the entire

real line as long as F (x) is periodic. However, most functions encountered

in physical applications are deﬁned in some interval (a, b) without repetition

beyond that interval. It would be useful if we could also expand such functions

in some form of Fourier “series.”

One way to do this is to start with the periodic series and then let the

period go to inﬁnity while extending the domain of the deﬁnition of the func-

tion. As a speciﬁc case, suppose we are interested in representing a function

f(x) that is deﬁned only for the interval (a, b) and is assigned the value zero

694 Integral Transforms

f (x)

b = a+L

a+L

+aa–L 2L

(a)

(b)

Figure 29.1: (a) The function we want to represent. (b) The Fourier series represen-

tation of the function.

everywhere else [see Figure 29.1(a)]. To begin with, we might try the Fourier

series representation, but this will produce a repetition of our function. This

situation is depicted in Figure 29.1(b).

Next we may try a function f

(x) deﬁned in the interval (a−Λ/2,b+Λ/2),

where Λ is an arbitrary positive number:

(x)=

⎧

⎪

⎨

⎪

⎩

0ifa − Λ/2 <x<a,

f(x)ifa<x<b,

0ifb<x<b+Λ/2.

This function, which is depicted in Figure 29.2, has the Fourier series repre-

sentation [see Equation (18.23)]

(x)=

√

L +Λ

∞



n=−∞

Λ,n

2iπnx/(L+Λ)

, (29.2)

where

Λ,n

√

L +Λ

b+Λ/2

a−Λ/2

−2iπnx/(L+Λ)

(x) dx. (29.3)

We have managed to separate various copies of the original periodic func-

tion by Λ. It should be clear that if Λ →∞, we can completely isolate the

function and stop the repetition. Let us investigate the behavior of Equations

(29.2) and (29.3) as Λ grows without bound. First, we notice that the quan-

tity k

deﬁned by k

≡ 2nπ/(L + Λ) and appearing in the exponent becomes

almost continuous. In other words, as n changes by one unit, k

changes only

slightly. This suggests that the terms in the sum in Equation (29.2) can be

lumped together in j intervals of width Δn

, giving

(x) ≈

∞



j=−∞

)

√

L +Λ

Δn

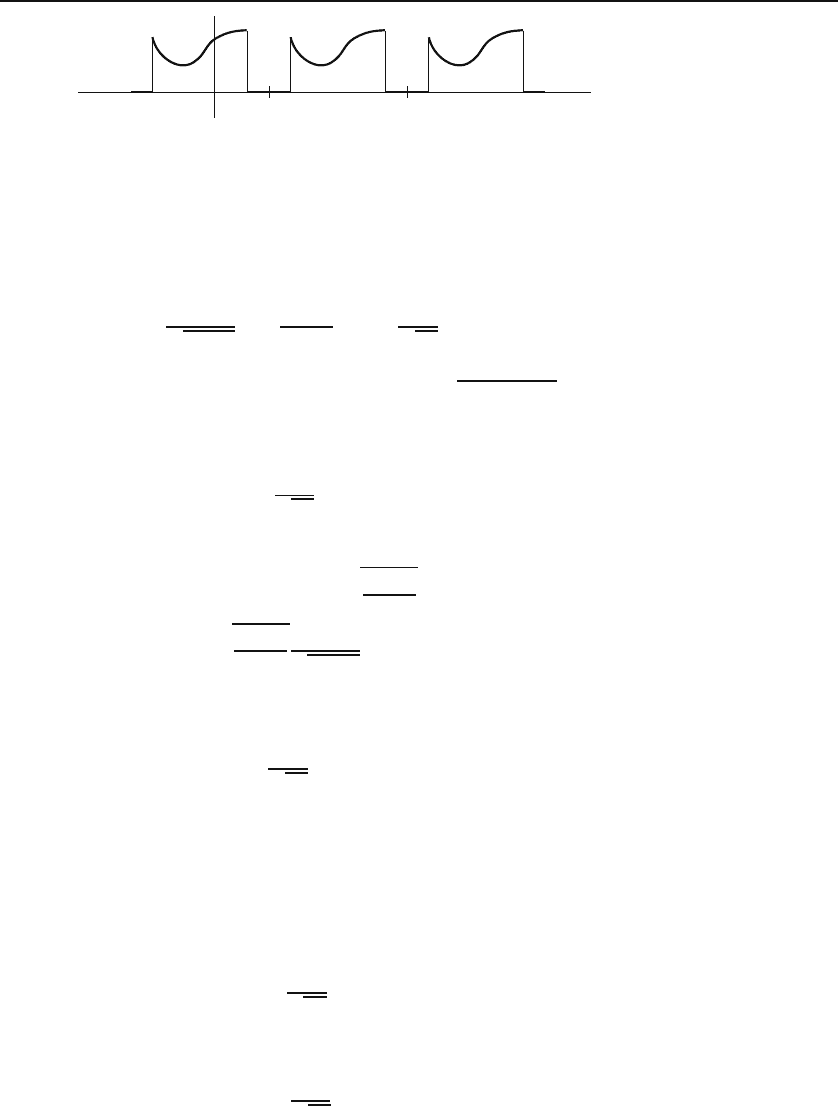
29.1 The Fourier Transform 695

a–Λ/2

b+Λ/2

Figure 29.2: By introducing the parameter Λ, we have managed to separate the copies

of the function.

where k

≡ 2n

π/(L +Λ), and f

) ≡ f

Λ,n

. Substituting Δn

=[(L +

Λ)/2π]Δk

in the above sum, we obtain

(x) ≈

∞



j=−∞

)

√

L +Λ

2π

Δk

√

2π

∞



j=−∞

Δk

where we introduced

) deﬁned by

) ≡



(L +Λ)/2πf

). It is

now clear that the preceding sum approaches an integral in the limit that

Λ →∞. In the same limit, f

(x) → f (x), and we have

f(x)=

√

2π

∞

−∞

f(k)e

ikx

dk, (29.4)

where

Fourier and

inverse Fourier

transforms

f(k) ≡ lim

Λ→∞

) = lim

Λ→∞



L +Λ

2π

)

= lim

Λ→∞



L +Λ

2π

√

L +Λ

b+Λ/2

a−Λ/2

−ik

(x) dx,

f(k)=

√

2π

∞

−∞

f(x)e

−ikx

dx. (29.5)

The function f in (29.4) is called the Fourier transform of

f and

f in (29.5)

is called the inverse Fourier transform of f . Note that the diﬀerence

between the two transforms is the sign of the exponential in the integrand.

Another notation that is commonly used for Fourier transform of a func-

tion f is F[f]. The inverse Fourier transform of a function g is then denoted

by F

−1

[g]. This means that F[f]isafunction whose value at x is given by

F[f](x)=

√

2π

∞

−∞

f(k)e

ikx

dk, (29.6)

Similarly, F

−1

[g] is a function whose value at k is given by

−1

[g](k)=

√

2π

∞

−∞

g(x)e

−ikx

dx, (29.7)

696 Integral Transforms

Note that the use of k and x in these two equations is completely arbitrary.

The only requirement is that the function and the variable in its argument

on the left appear, respectively, in the integrand and in the exponent on the

right. For example, (29.6) could be written as

F[f](k)=

√

2π

∞

−∞

f(x)e

ikx

dx, or F[h](t)=

√

2π

∞

−∞

h(ω)e

iωt

dω,

and (29.7) as

−1

[g](x)=

√

2π

∞

−∞

g(k)e

−ikx

dk or F

−1

[f](y)=

√

2π

∞

−∞

f(x)e

−ixy

dx.

29.1.1 Properties of Fourier Transform

Equations (29.4) and (29.5) are reciprocals of one another. However, it is not

obvious that they are consistent. In other words, if we substitute (29.4) in

the RHS of (29.5), do we get an identity? Let’s try this:

f(k)=

√

2π

∞

−∞

dx e

−ikx



√

2π

∞

−∞

f(k









2π

∞

−∞

∞

−∞

f(k



i(k



−k)x



We now change the order of the two integrations:

f(k)=

∞

−∞



f(k



)



2π

∞

−∞

dx e

i(k



−k)x



But the expression in the square brackets is the Dirac delta function given by

Equation (18.28). Thus, we have

f(k)=



∞

−∞



f(k



)δ(k



− k), which is an

identity. In the F notation, this result can be written as

−1

F[f]=FF

−1

[f]=f, (29.8)

for any function f . The second identity can be shown similarly. Another

property enjoyed by the Fourier transform and its inverse in linearity.Ifa

and b are constants and f and g functions, then

F[af + bg]=aF[f]+bF[g], and F

−1

[af + bg]=aF

−1

[f]+bF

−1

[g].

(29.9)

It is useful to generalize Fourier transform equations to more than one

dimension. The generalization is straightforward:

f](r) ≡ f(r)=

(2π)

n/2

∞

ik·r

f(k),

−1

[f](k) ≡

f(k)=

(2π)

n/2

∞

xf(r)e

−ik·r

. (29.10)

where n is usually 2 or 3, Ω

∞

is the entire k-space, and Ω

∞

is the entire

x-space.

29.1 The Fourier Transform 697

29.1.2 Sine and Cosine Transforms

The complex exponential in the deﬁnition of Fourier transform or its inverse

can be broken down into its trigonometric parts. Then for an even function,

the cosine part contributes and for an odd function, the sine part contributes.

In either case, the integration



∞

−∞

can be equated to 2



∞

. This leads to

the sine transform and cosine transform denoted by F

[f]andF

[f],

respectively, for any function:

Sine and cosine

transforms

[f](x)=



∞

f(k)sinkxdk,

[f](x)=



∞

f(k)coskxdk. (29.11)

What is the inverse of a cosine transform? To ﬁnd out, let F (x)denote

the left-hand side of the second equation in (29.11). Multiply both sides of

the equation by cos k



x—with k



> 0—and integrate over all positive values

of x to get

∞

F (x)cosk



xdx =



∞

f(k)dk

∞

cos kx cos k



xdx. (29.12)

Writing the cosines in terms of exponential, the x integration on the right

gives

∞

cos kx cos k



xdx =

∞

ikx

+ e

−ikx





+ e

−ik





∞

ix(k+k



)

+ e

−ix(k+k



)

+ e

ix(k−k



)

+ e

−ix(k−k



)

∞

−∞

ix(k+k



)

dx +

∞

−∞

ix(k−k



)

[δ(k + k



)+δ(k − k



)] .

To go from the second to third line, we used



∞

−iax

dx =



−∞

iax

dx,which Inverses of sine

and cosine

transforms

the reader can easily verify; and to go from the third to the last line, we used

Equation (18.28). Substituting the last result in (29.12), we obtain

∞

F (x)cosk



xdx =



∞

f(k)δ(k + k



)dk

  

=0 (Reader, why?)



∞

f(k)δ(k − k



)dk



f(k



f(k





∞

F (x)cosk



xdx.

698 Integral Transforms

This shows that the inverse of a cosine transform is another cosine trans-

form. Similarly, one can show that the inverse of a sine transform is another

sine transform. We shall not use sine or cosine transforms, as the Fourier

transform, with the exponential in the integrand, is much more convenient.

29.1.3 Examples of Fourier Transform

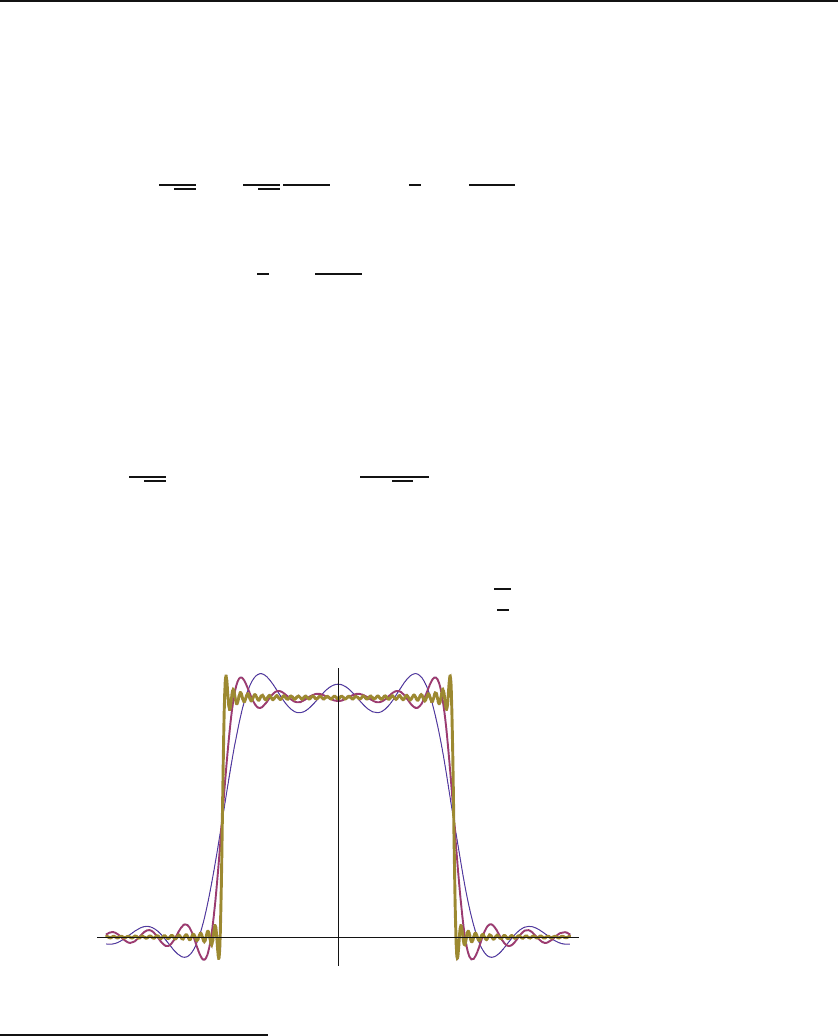
Example 29.1.1. Let us evaluate the inverse Fourier transform of the function

deﬁned by

f(x)=

b if |x| <a,

0if|x| >a

(see Figure 29.3). From (29.5) and (29.7) we have

−1

[f](k) ≡

f(k)=

√

2π

∞

−∞

f(x)e

−ikx

dx =

√

2π

−a

−ikx

dx =

2ab

√

2π



sin ka



which is the function encountered on page 491 and depicted in Figure 18.7.

This result deserves some detailed discussion. First, note that if a →∞,the

function f(x) becomes a constant function over the entire real line, and we get

f(k)=

√

2π

lim

a→∞

sin ka

√

2π

πδ(k)

by Equation (18.27). This is the Fourier transform of an everywhere-constant func-

tion (see Problem 29.1). Next, let b →∞and a → 0 in such a way that 2ab,which

is the area under f(x), is 1. Then f(x) will approach the delta function, and

f(k)

becomes

f(k) = lim

b→∞

a→0

2ab

√

2π

sin ka

√

2π

lim

a→0

sin ka

√

2π

So the Fourier transform of the delta function is the constant 1/

√

2π as implied by

(29.5).

Finally, we note that the width of f(x)isΔx =2a, and the width of

f(k)is

roughly the distance, on the k-axis, between its ﬁrst two roots, k

and k

−

,oneither

side of k =0: Δk = k

− k

−

=2π/a. Thus increasing the width of f(x)results

in a decrease in the width of

f(k). In other words, when the function is wide, its

Fourier transform is narrow. In the limit of inﬁnite width (a constant function), we

get inﬁnite sharpness (the delta function). The last two statements are very general.

In fact, it can be shown that ΔxΔk ≥ 1 for any function f(x). When both sides

–a

(x)

Figure 29.3: The square “bump” function.

29.1 The Fourier Transform 699

of this inequality are multiplied by the (reduced) Planck constant  ≡ h/(2π), the

result is the celebrated Heisenberg uncertainty relation:

Heisenberg

uncertainty

relation

ΔxΔp ≥ ,

where p = k is the momentum of the particle.

Having obtained the transform of f(x), we can write

f(x)=

√

2π

∞

−∞

√

2π

sin ka

ikx

dk =

∞

−∞

sin ka

ikx

dk.

Figure 29.4 shows the integral

−K

sin ka

ikx

when K = 10, K = 20, and K = 100. It is seen that by making the limits

of integration larger and larger, the graph approximates Figure 29.3 better and

better.



Example 29.1.2. Let us evaluate the Fourier transform of a Gaussian g(x)=

−bx

with a, b > 0:

˜g(k)=

√

2π

∞

−∞

−b(x

+ikx/b)

dx =

−k

/4b

√

2π

∞

−∞

−b(x+ik/2b)

dx.

To evaluate this integral rigorously, we would have to use the calculus of residues

developed in Chapter 21. However, we can ignore the fact that the exponent is

complex, substitute y = x + ik/(2b), and write

∞

−∞

−b[x+ik/(2b)]

dx =

∞

−∞

−by

dy =



Figure 29.4: The thinnest plot represents K =10; the next thinnest plot represents

K =20; and the thickest plot represents K = 100.

In the context of the uncertainty relation, the width of the function—the so-called

wave packet—measures the uncertainty in the position x of a quantum mechanical particle.

Similarly, the width of the Fourier transform measures the uncertainty in k, which is related

to momentum p via p = k.

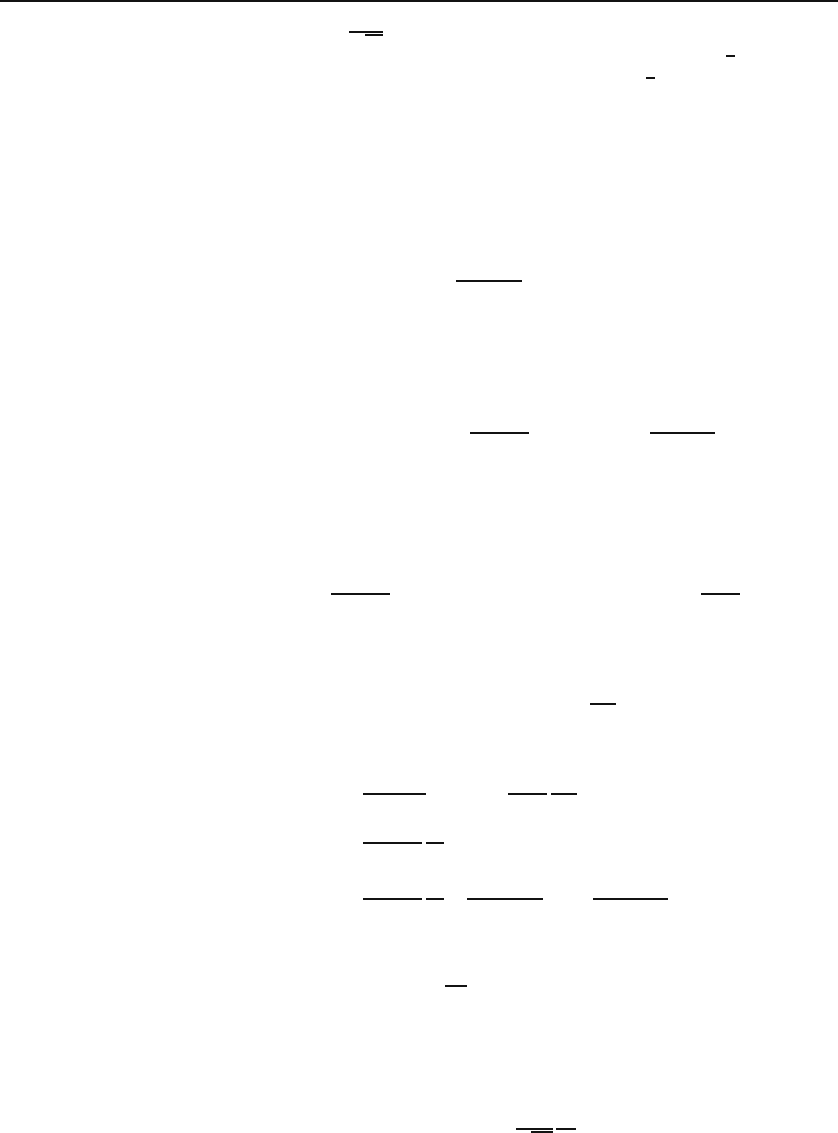
700 Integral Transforms

Thus,wehave˜g(k)=

√

−k

/(4b)

, which is also a Gaussian.

We note again that the width of g(x), which is proportional to 1/

√

b,isininverse

relation to the width of ˜g(k), which is proportional to

√

b. WethushaveΔxΔ

k ∼ 1.



Example 29.1.3. In this example we evaluate the inverse Fourier transform of the

Coulomb potential V (r)ofapointchargeq at the origin: V (r)=k

q/r.Theinverse

Fourier transform is important in scattering experiments with atoms, molecules, and

solids. As we shall see in the following, the inverse Fourier transform of V (r)isnot

deﬁned. However, if we work with the Yukawa p otential,Yukawa potential

(r)=

−αr

,α>0,

the inverse Fourier transform will be well-deﬁned, and we can take the limit α → 0

to recover the Coulomb potential. Thus, we seek the inverse Fourier transform of

(r).

We are working in three dimensions and therefore may write

−1

](k) ≡

(k)=

(2π)

3/2

∞

−ik·r

−αr

It is clear from the presence of r that spherical coordinates are appropriate. We

are free to pick any direction as the z-axis. A simplifying choice in this case is the

direction of k.So,weletk = |k|

= k

,ork · r = kr cos θ,whereθ is the polar

angle in spherical coordinates. Now we have

(k)=

(2π)

3/2

∞

sin θdθ

2π

dϕe

−ikr cos θ

−αr

The ϕ integration is trivial and gives 2π.Theθ integration simpliﬁes if we make

the substitution u =cosθ:

sin θe

−ikr cos θ

dθ =

−1

−ikru

du =

ikr

− e

−ikr

We thus have

(k)=

q(2π)

(2π)

3/2

∞

dr r

−αr

ikr

− e

−ikr

)

(2π)

1/2

∞

(−α+ik)r

− e

−(α+ik)r

(2π)

1/2



(−α+ik)r

−α + ik



∞

−(α+ik)r

α + ik



∞



Note how the factor e

−αr

has tamed the divergent behavior of the exponential at

r →∞. This was the reason for introducing it in the ﬁrst place. Simplifying the last

expression yields

(k)=(2k

√

2π)(k

+ α

)

−1

. The parameter α is a measure of

the range of the potential. It is clear that the larger α is, the smaller the range. In

fact, it was in response to the short range of nuclear forces that Yukawa introduced

α. For electromagnetism, where the range is inﬁnite, α becomes zero and V

(r)

reduces to V (r). Thus, the inverse Fourier transform of the Coulomb potential is

Coul

(k)=

√

2π