Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

29.3 The Laplace Transform 721

Using partial fraction techniques, we can write this as

Aω

+ ω

)(s

+ γs + ω

)

γω

+ γs + ω

−

γω

+ ω

Each term can now be inverted using the results we have obtained in several exam-

ples. Denoting the ﬁnal result by Φ(t), we get

Φ(t) ≡ L

−1



L[f](s)

+ γs + ω



= −

γω

cos ω

t +

γω

−γt/2



cos Ωt +

2Ω

sin Ωt



Note that Φ(0) = 0 as expected from the discussion above. Diﬀerentiating, we

obtain

Φ(t)=

sin ω

t −

2ω

−γt/2



cos Ωt +

2Ω

sin Ωt



γω

−γt/2



−ΩsinΩt +

cos Ωt



It is readily veriﬁed that

Φ(0) = 0 as explained above. Substituting Φ(t)forthe

last term of (29.70) yields

x(t)=e

−γt/2



cos Ωt +

˙x

+ x

γ/2

sin Ωt



−

γω

cos ω

t +

γω

−γt/2



cos Ωt +

2Ω

sin Ωt



. (29.71)

After a long time (i.e., as t →∞), the terms containing an exponential—the so-

called transient terms—will be negligible and x(t) →−

γω

cos ω

t as expected from

the elementary analysis of the same problem.



We can understand this interesting behavior of Φ(t)intermsoftheprop-

erties of convolution. Let g(t) be the inverse transform of 1/(s

+ γs + ω

Then invoking Box 29.3.1, the last term of (29.70) can be written as

Φ(t)=L

−1

L[f](s) · L[g](s)

=(f ∗ g)(t)=

f(u)g(t − u)du,

whose derivative is (see Box 3.2.2)

Φ(t)=f(t)g(0) +

f(u)˙g(t − u)du.

It is now clear why Φ(0) = 0. As for the derivative, we see that

Φ(0) =

f(0)g(0). But g(t) is given by (29.69) which is clearly 0 at t =0.

29.3.4 Inverse of Laplace Transform

As mentioned earlier, the procedure for inverting a Laplace transform is im-

portant in solving diﬀerential equations, as the technique—like any other

transform—yields the transform of the solution, and to get the solution, one

has to invert that transform. So far, we have used various tricks and prop-

erties of the Laplace transform to get from F (s) ≡ L[f](s)tof(t). Now, we

722 Integral Transforms

provide a general formula that can always be used to yield the function. The

procedure is the Mellin inversion integral:

Mellin inversion

integral

f(t)=

2πi

γ+i∞

γ−i∞

F (s)e

ds. (29.72)

The integration is along a line, called the Bromwich contour, parallel to

Bromwich contour

the imaginary axis of the complex s plane. The real number γ is arbitrary as

long as the integration line is to the right of all the singularities of F (s). To

ﬁnd the actual value of the integral, one closes the contour with an inﬁnite

semicircle to the left of the line and uses the residue theorem.

To prove that the right-hand side of (29.72) is indeed f(t), substitute the

deﬁnition of F (s),

F (s)=

∞

f(τ)e

−sτ

dτ,

in the integral and switch the order of integrations to get

RHS =

2πi

∞

f(τ)dτ

γ+i∞

γ−i∞

s(t−τ)



 

Denote this by J

. (29.73)

Introduce a new variable of integration σ by s = γ + iσ in the inner integral

to get

J =

∞

−∞

(γ+iσ)(t−τ )

idσ = ie

γ(t−τ )

∞

−∞

iσ(t−τ)

dσ



 

=2πδ(t−τ) by (18.28)

=2πiδ(t − τ ).

The last step follows because δ(t − τ) = 0 unless t = τ in which case the

exponent of the exponential is zero. Substituting this in (29.73) and noting

that τ>0, we get RHS = f (t).

To see why the integration line must lie to the right of all singularities,

take the Laplace transform of both sides of (29.72):

L[f(t)] =

2πi

∞

−st



γ+i∞

γ−i∞

F (σ)e

σt

dσ



2πi

γ+i∞

γ−i∞

F (σ)dσ

∞

(σ−s)t

dt = −

2πi

γ+i∞

γ−i∞

F (σ)

σ − s

dσ,

assuming that Re(s) > Re(σ)=γ.IfF (σ) is analytic to the right of the

Bromwich contour, then closing the inﬁnite semicircle on the right, there will

be a single pole at σ = s inside the closed contour, and the residue theorem

gives the value of the integral as −2πiF(s), with the negative sign coming

from the clockwise integration. If any of the poles of F were on the right of

the Bromwich contour we would not obtain −2πiF(s) for the integration.

29.4 Problems 723

Example 29.3.8. Let us ﬁnd the inverse Laplace transform of F (s)=1/(s

+ω

This is given by

f(t)=

2πi

γ+i∞

γ−i∞

+ ω

where the contour of integration includes the inﬁnite semicircle to the left. The

poles of the integrand are at ±iω,soaslongasγ>0, the contour encloses both

poles. The residue theorem then yields

f(t)=

2πi

Res



(s − iω)(s + iω)





s=iω

+Res



(s − iω)(s + iω)





s=−iω

iωt

2iω

−iωt

−2iω

sin ωt

which is the expected result (see Example 29.3.1).



We can similarly ﬁnd the inverse Laplace transform of F (s)=s/(s

+ ω

f(t)=

2πi

γ+i∞

γ−i∞

+ ω

The contour of integration again includes the inﬁnite semicircle to the left,

and the poles of the integrand are at ±iω, as above. The residue theorem now

yields

f(t)=

2πi

(

2πi



Res



(s − iω)(s + iω)





s=iω

+Res



(s − iω)(s + iω)





s=−iω

iωe

iωt

2iω

−iωe

−iωt

−2iω

=cosωt

which is also treated in Example 29.3.1.

29.4 Problems

29.1. Find directly the Fourier transform of

(a) the constant function f(x)=C,and

(b) the Dirac delta function δ(x).

29.2. Show the second identity in (29.8).

29.3. Show that the inverse of a sine transform is another sine transform.

29.4. Show (29.9), the linearity property of Fourier transform and its inverse.

29.5. Suppose that

f(k) is the inverse Fourier transform of f (x). Show that

the inverse Fourier transform of f(x + a)ise

iak

f(k).

724 Integral Transforms

29.6. Show that if f(t)=cosω

t,then

f(ω)=



[δ(ω − ω

)+δ(ω + ω

)] .

29.7. Show that

(a) g(x) is real if and only if ˜g

∗

(k)=˜g(−k),

(a) g(x) is imaginary if and only if ˜g

∗

(k)=−˜g(−k), and

29.8. Evaluate the Fourier transform of

g(x)=

b −b|x|/a if |x| <a,

0if|x| >a.

29.9. Let

f(t)=

sin ω

t if |t| <T,

0if|t| >T.

Show that

f(ω)=

√

2π

(

sin[(ω − ω

)T ]

ω − ω

−

sin[(ω + ω

)T ]

ω + ω

)

Verify the uncertainty relation ΔωΔt ≈ 4π.

29.10. If f(x)=g(x + a), show that

f(k)=e

−iak

˜g(k).

29.11. For a>0 ﬁnd the Fourier transform of f (x)=e

−a|x|

.Is

f(k)sym-

metric? Is it real? Verify the uncertainty relations.

29.12. The displacement of a damped harmonic oscillator is given by

f(t)=

−αt

iω

if t>0,

0ift<0.

Find

f(ω) and show that the frequency distribution |

f(ω)|

is given by

f(ω)|

2π

(ω − ω

)

+ α

29.13. Prove the convolution theorem for Fourier transform:

convolution

theorem for

Fourier transform

∞

−∞

f(x)g(y − x) dx =

∞

−∞

f(k)˜g(k)e

iky

dk.

What will this give when y =0?

29.14. Prove Parseval’s relation for Fourier transforms:

Parseval’s relation

∞

−∞

f(x)g

∗

(x) dx =

∞

−∞

f(k)˜g

∗

(k) dk.

29.4 Problems 725

29.15. Find the sine and cosine transform of e

−ax

29.16. Following Example 29.1.6, substitute the Fourier Transform of the

wave function Ψ(x, t) in the one-dimensional wave equation

∂

∂t

∂

∂x

and solve the diﬀerential equation in t to get

Ψ(k, t)=C(k)e

±ickt

Assuming that the initial shape of the wave Ψ(x, 0) is given by a function

f(x), show that the solution Ψ(x, t) can be written as

Ψ(x, t)=f (x ±ct).

29.17. Show the relation used in Example 29.3.6:

− tan

−1





=tan

−1





Hint: Let x denote the left-hand side and α =tan

−1

(s/ω). Take the tan of

both sides of the deﬁnition of x and use cot α =tan(π/2 − α)=1/ tan α.

29.18. Let f(t)=sinωt be the periodic function of (29.61) and verify that

the equation holds (for T =2π/ω). Do the same for f(t)=cosωt.

29.19. Find the Laplace transform of the periodic sawtooth function with

period T deﬁned by

V (t)=V

for 0 ≤ t<T.

29.20. Find the Laplace transform of 2t +4e

− 3cos3t.

29.21. Compute L[cosh

γt]andL[sinh

γt].

29.22. Compute L[cos

ωt]andL[sin

ωt] directly from the deﬁnition of Laplace

transform. Now show that

L[cos

ωt]=L[1] −L[sin

ωt].

29.23. A function N(t) is called a null function if

N(u) du =0

for all t>0. Show that L[N(t)] = 0.

29.24. Compute L[e

sin 3t], L[t

−γt

], L

−1

−2s

], and

−1



−

−bs



726 Integral Transforms

29.25. Find L[e

√

t], L[

√

t], and L

−1

−2s

√

s].

29.26. (a) Show that

∂

∂ν

ν−1

= t

ν−1

ln t.

(b) Now use (29.52) to prove that

L[t

ν−1

ln t]=



(ν) − Γ(ν)lns

29.27. Using Laplace transform, solve the following initial-value problems

(a)

+4x =sint, x(0) = 1, ˙x(0) = 0

(b)

− 2

− 3y = te

,x(0) = 2, ˙x(0) = 1

(c)

= θ(1 − t),x(0) = 1, ˙x(0) = −1, where θ is the step

function.

(d)

+ x = θ(π − t)cost, x(0) = 0, ˙x(0) = 0, where θ is the step

function.

29.28. Using Laplace transform, solve the following boundary-value problems

(a)

+ ω

x =sinωt, x(0) = 1,x(

2ω

)=π.

(b)

+ ω

x = t, x(0) = 1, ˙x(

)=−1.

29.29. Find L

−1

[

+2s+5

]andL

−1

[

−a

] using Mellin inversion integral

(29.72).

Chapter 30

Calculus of Variations

In a typical multivariable extremum problem, you are given a function of n

variables f (x

,...,x

) and asked to ﬁnd those n values of the variables

that maximize or minimize the function. The procedure is, of course, to set

the partial derivative of the function with respect to each variable equal to

zero and solve the resulting equations.

Geometrically, f is a function in an n-dimensional space, and the problem

is to ﬁnd the point in that space at which f has the highest (or lowest)

value compared to the neighboring points. There is another geometric way

of looking at the extremum problem. Think of (x

,...,x

) as a piecewise New way of

looking at the

multivariable

extremum problem

linear path in a two-dimensional coordinate system. The horizontal axis is

restricted to the values 1, 2,...,n, and for each of these values i the value of

the corresponding variable x

determines one point with coordinates (i, x

Connecting the neighboring points by a straight line segment produces the

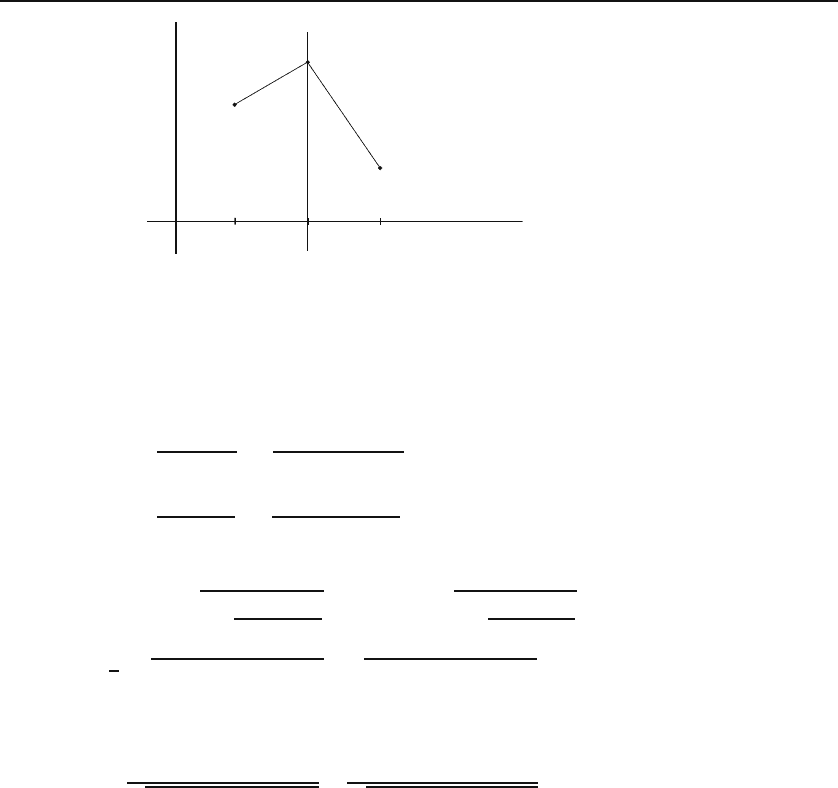
path. Figure 30.1 shows a couple of such paths.

Figure 30.1: For each integer i between 1 and n, pick the real number x

and draw

a point with coordinates (i, x

). Connect these points to form a path. Two such paths

are shown for n =5.

728 Calculus of Variations

The extremum problem can now be stated in terms of paths: Find the path

for which f has either the largest or the smallest value compared with its value

at the neighboring paths. And to do so, we diﬀerentiate with respect to a point

of the path. But let’s be more general in anticipation of the problems typical

of this chapter. Let x

be a variable where α is not necessarily an integer

between 1 and n. Diﬀerentiate the function with respect to x

and set the

result equal to zero:

∂f

∂x



i=1

∂f

∂x



i=1

∂f

∂x

αi

=0. (30.1)

If α is not equal to one of the integers between 1 and n, the sum vanishes

identically, i.e., the left-hand side is identically zero because f is not a function

of x

. However, if α is one of the integers between 1 and n, (30.1) gives one

of the equations to be solved for determining the extremizing path.

30.1 Variational Problem

Our treatment of the extremum problem above in terms of paths was mo-

tivated by situations in which variations of smooth paths are to be consid-

ered. A typical variational problem has a function whose value depends

on the path, i.e., it takes a path and puts out a number. We say that it is a

functional, because its argument is a function rather than a set of numbers.

Functional deﬁned

If L is a functional and x(t) represents a path in the tx-plane, then the value

of the functional for this path is represented by L[x]. The most common func-

tional integrates a certain function of x(t)and ˙x(t)oversomeinterval(a, b).

If L(x, ˙x, t) is such a function, then

L[x]=

x(t), ˙x(t),t

dt. (30.2)

For every path, the integrand becomes a function of t which can be integrated

to give a single number, and the variational problem asks for the path that

yields either the largest or the smallest such number.

Example 30.1.1.

Before delving into formalism, let’s look at a very simple con-

creteexample. TaketwopointsP

=(a, y

)andP

=(b, y

)inthexy-plane.

Consider points P

a+b

,Y) lying on the perpendicular bisector of the interval

(a, b), and the path consisting of the line segments

and P

as shown in

Figure 30.2. For what value of Y is the length of this path minimum?

The length L of the path is given by

L =



+ dy





dx. (30.3)

30.1 Variational Problem 729

Figure 30.2: Here, a path consists of only two line segments. The middle point P

is constrained to move on the vertical line on which it is located to produce diﬀerent

paths.

The equation of the path can be shown to be

y(x)=

⎧

⎪

⎨

⎪

⎩

2(Y − y

)

b − a

x +

(a + b)y

− 2aY

b − a

if a<x<(a + b)/2,

2(y

− Y )

b − a

x +

2bY − (a + b)y

b − a

if (a + b)/2 <x<b.

Substituting this in the integral gives

L =

(a+b)/2

4(Y − y

)

(b − a)

dx +

(a+b)/2

4(y

− Y )

(b − a)



(b − a)

+4(Y − y

)



(b − a)

+4(y

− Y )

Diﬀerentiating with respect to Y and setting the result equal to zero leads to the

following equation:

Y − y



(b − a)

+4(Y − y

)

− Y



(b − a)

+4(y

− Y )

Square both sides and simplify to get Y − y

= y

− Y , whose solution is Y =

+ y

)/2, placing P

on the line joining P

and P

. Thus among all the paths

the shortest is the straight line joining P

and P



30.1.1 Euler-Lagrange Equation

The preceding example showed that from among paths consisting of two spe-

ciﬁc straight line segments, the one whose middle point lies on the straight

line joining the two end points gives the shortest length. What if the point

is not on the perpendicular bisector of (a, b), or if the path has more than

three points? There is a procedure which picks the minimizing path from

among all possible paths. Let’s discuss this procedure.

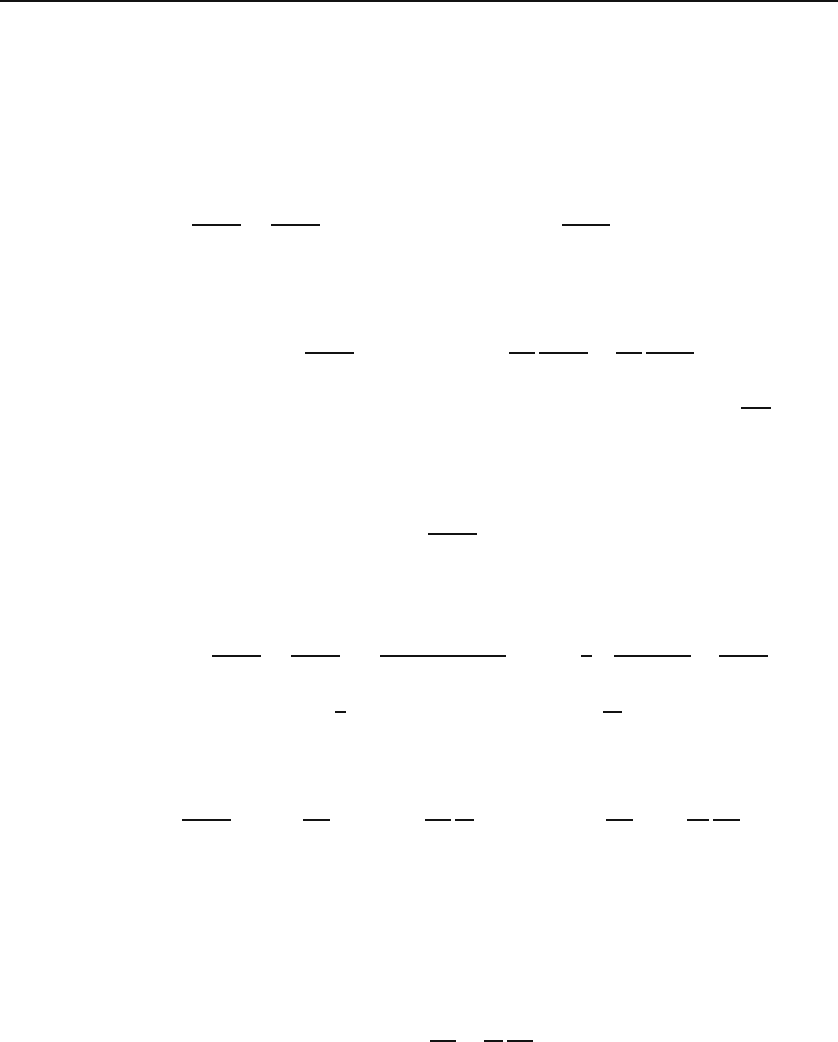
730 Calculus of Variations

Going back to Equation (30.2), we ask if there is a process whereby one

can take the derivative of L[x], set it equal to zero, and solve for the desired

path. Is there a derivative with respect to a path? To ﬁnd out, let’s see if

Functional

derivative

explained

we can generalize (30.1) from the discrete case of a path consisting of only n

points to a continuous path. The derivative with respect to a path is called

a functional derivative and δ is used instead of ∂ to symbolize it. So, let’s

write

δL[x]

δx(τ)

x(t), ˙x(t),t

dt =

δx(τ)

x(t), ˙x(t),t

dt. (30.4)

In analogy with (30.1), and noting that L is to be considered as an ordinary

function (not functional) of x,˙x,andt,wehave

δx(τ)

x(t), ˙x(t),t

∂L

∂x

δx(t)

δx(τ)

∂L

∂ ˙x

δ ˙x(t)

δx(τ)

, (30.5)

because t is independent of x(τ). In the discrete case, we had

∂x

= δ

αi

What is the generalization of the Kronecker delta to the continuous case?

The Dirac delta function! This can be shown more rigorously, but the proof

is outside the scope of this book. So, let’s write the fundamental functional

derivative:

A fundamental

functional

derivative

δx(t)

δx(τ)

= δ(t − τ). (30.6)

What about the functional derivative in the second term of (30.5)? Using

the deﬁnition of the derivative and (30.6), we have

Another

fundamental

functional

derivative

δ ˙x(t)

δx(τ)

lim

→0

x(t + ) −x(t)



= lim

→0







δx(t + )

δx(τ)

−

δx(t)

δx(τ)



= lim

→0





δ(t +  −τ) −δ(t −τ)





δ(t − τ). (30.7)

Putting (30.6) and (30.7) in (30.5) and the result in (30.4), we obtain

δL[x]

δx(τ)



∂L

∂x

δ(t − τ)+

∂L

∂ ˙x

δ(t −τ)



dt =

∂L

∂x

(τ) −

dτ

∂L

∂ ˙x

(τ), (30.8)

where in the last step we used the properties of the Dirac delta function and

its derivative as given in (5.10) and (5.11). We have assumed that τ lies in

the interval (a, b).

Having found the functional derivative, we now equate it to zero and ﬁnd

the equation that determines the path—the function x(t)—which extremizes

the functional. The equation is

Euler-Lagrange

equation

∂L

∂x

−

∂L

∂ ˙x

=0, (30.9)

andiscalledtheEuler-Lagrange equation. Itisattheheartofallvaria-

tional problems. If we know the function L, we can diﬀerentiate it, substitute