Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

30.2 Lagrangian Dynamics 741
By equating the first term of (30.15) to the first term of the last equation in
(30.37), we get
∂L
∂x
=
∂
∂x
(−Φ).
Antidifferentiation yields L = −Φ(x, y, z)+f(y, z, ˙x, ˙y, ˙z), where f is the
“constant” of integration. If the partials of L with respect to y and z are to
be equal to the corresponding partials of −Φ, then f cannot depend on y and
z.So,f is a function of velocity components. If the second term of (30.37) is
to equal the second term of (30.15), then
m ˙x =
∂L
∂ ˙x
=
∂f
∂ ˙x
or f (˙x, ˙y, ˙z)=
1
2
m ˙x
2
+ g(˙y, ˙z),
where g(˙y, ˙z) is the “constant” of this new integration. Applying the same
argument to y and z, we conclude that f is just the kinetic energy. Therefore,
we arrive at the important conclusion that for a single particle with position
vector r, the extremization of
L(r,
˙
r,t)=−Φ(r)+
1
2
m |
˙
r|
2
= −Φ(x, y, z)+
1
2
m
˙x
2
+˙y
2
+˙z
2
!
(30.38)
gives the equation of motion of the particle. L(r,
˙
r,t) is called the Lagrangian
of a single particle moving in potential Φ.
For N non-interacting particles in an external potential, the Lagrangian
is the sum of the single-particle Lagrangians:
L =
N
i=1
L
i
=
N
i=1
−Φ
i
+
1
2
m
i
|
˙
r
i
|
2
=
N
i=1
.
−Φ
i
+
1
2
m
i
˙x
2
i
+˙y
2
i
+˙z
2
i
!/
,
where Φ
i
=Φ(x
i
,y
i
,z
i
). Note that this can be written as
L = KE − Φ, where KE =
N
i=1
1
2
m
i
˙x
2
i
+˙y
2
i
+˙z
2
i
!
, and Φ =
N
i=1
Φ
i
.
(30.39)
If the particles are interacting, then Φ is no longer the sum of individual
potentials, but a general function of all coordinates. It is therefore common to
collect all the N triple coordinates into one big 3N-component vector q and
call it the generalized coordinates vector. Then the Lagrangian is written
as
L (q,
˙
q,t)=KE − Φ=
3N
i=1
1
2
μ
i
˙q
2
i
− Φ(q
1
,q
2
,...,q
3N
). (30.40)
We changed the mass to μ
i
to avoid confusion with the m
i
of the previous
equation. For example, for three particles interacting gravitationally,
Φ(q
1
,q
2
,...,q
9
)=Φ(r
1
, r
2
, r
3
)=−
Gm
1
m
2
|r
1
− r
2
|
−
Gm
1
m
3
|r
1
− r
3
|
−
Gm
2
m
3
|r
2
− r
3
|
,
which can be written in terms of the q’s, once the latter are defined in terms
of the position vectors. Note that many of the μ
i
’s in (30.40) are equal. For
instance, if q
1
= x
1
, q
2
= y
1
,andq
3
= z
1
,thenμ
1
= μ
2
= μ
3
= m
1
,etc.
742 Calculus of Variations
r
X
θ
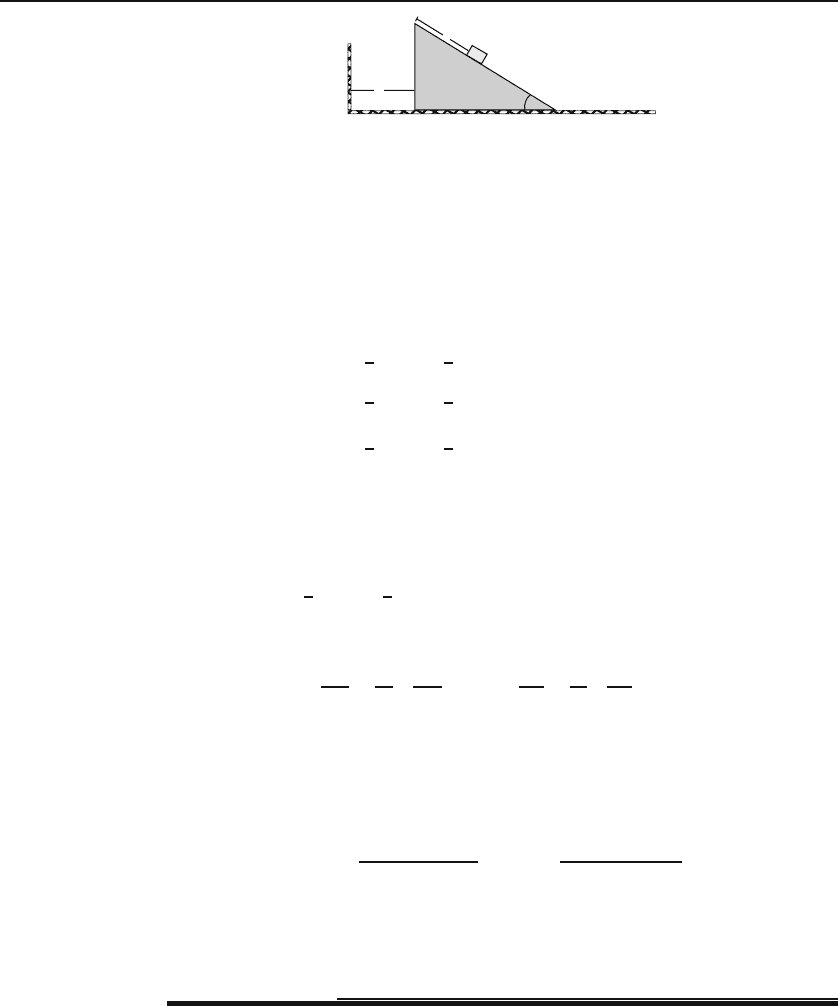
Figure 30.4: The inclined plane moves as m moves on it.
Example 30.2.1. Ablockofmassm slides on a frictionless inclined plane, which
has mass M and moves on a frictionless horizontal surface as shown in Figure 30.4.
The position of the incline is denoted by X and that of the block by r,or(x, y)with
x = X + r cos θ, y =(l −r)sinθ,
where l is the length of the inclined plane. The kinetic energy of the system is
KE =
1
2
M
˙
X
2
+
1
2
m
˙x
2
+˙y
2
!
=
1
2
M
˙
X
2
+
1
2
m
˙
X +˙r cos θ
2
+˙r
2
sin
2
θ
=
1
2
M
˙
X
2
+
1
2
m
˙
X
2
+˙r
2
+2
˙
X ˙r cos θ
,
and the potential energy
Φ=mgy = mg(l − r)sinθ,
giving rise to the Lagrangian
L =
1
2
M
˙
X
2
+
1
2
m
˙
X
2
+˙r
2
+2
˙
X ˙r cos θ
− mg(l − r)sinθ.
The equations of motion
∂L
∂X
−
d
dt
∂L
∂
˙
X
=0,
∂L
∂r
−
d
dt
∂L
∂ ˙r
=0,
can now be calculated:
−M
¨
X −m
¨
X +¨r cos θ
=0,mgsin θ − m
¨r +
¨
X cos θ
=0.
Solving for the two accelerations, we get
¨
X =
−mg sin θ cos θ
M + m sin
2
θ
, ¨r =
(m + M )g sin θ
M + m sin
2
θ
.
Note that for an infinitely heavy inclined plane,
¨
X =0and¨r = g sin θ,as
expected.
Historical Notes
was born Giuseppe Luigi Lagrangia but adopted the French version of his name. He
was the eldest of eleven children, most of whom did not reach adulthood. His father
destined him for the law—a profession that one of his brothers later pursued—
and Lagrange offered no objections. But having begun the study of physics and
geometry, he quickly became aware of his talents and henceforth devoted himself to

30.2 Lagrangian Dynamics 743
the exact sciences. Attracted first by geometry, at the age of seventeen he turned
to analysis, then a rapidly developing field.
In 1755, in a letter to the geometer Giulio da Fagnano, Lagrange speaks of
one of Euler’s papers published at Lausanne and Geneva in 1744. The same letter
shows that as early as the end of 1754 Lagrange had found interesting results in
this area, which was to become the calculus of variations (a term coined by Euler
Joseph Louis
Lagrange
1736–1813
in 1766). In the same year, Lagrange sent Euler a summary, written in Latin, of
the purely analytical method that he used for this type of problem. Euler replied
to Lagrange that he was very interested in the technique. Lagrange’s merit was
likewise recognized in Turin; and he was named, by a royal decree, professor at the
Royal Artillery School with an annual salary of 250 crowns—a sum never increased
in all the years he remained in his native country. Many years later, in a letter
to d´Alembert, Lagrange confirmed that this method of maxima and minima was
the first fruit of his studies—he was only nineteen when he devised it—and that he
regarded it as his best work in mathematics.
In 1756, in a letter to Euler that has been lost, Lagrange, applying the calculus of
variations to mechanics, generalized Euler’s earlier work on the trajectory described
by a material point subject to the influence of central forces to an arbitrary system
of bodies, and derived from it a procedure for solving all the problems of dynamics.
In 1757 some young Turin scientists, among them Lagrange, founded a scientific
society that was the origin of the Royal Academy of Sciences of Turin. One of the
main goals of this society was the publication of a miscellany in French and Latin,
Miscellanea Taurinensia ou M´elanges de Turin, to which Lagrange contributed fun-
damentally. These contributions included works on the calculus of variations, prob-
ability, vibrating strings, and the principle of least action.
To enter a competition for a prize, in 1763 Lagrange sent to the Paris Academy
of Sciences a memoir in which he provided a satisfactory explanation of the trans-
lational motion of the moon. In the meantime, the Marquis Caraccioli, ambassador
from the kingdom of Naples to the court of Turin, was transferred by his government
to London. He took along the young Lagrange, who until then seems never to have
left the immediate vicinity of Turin. Lagrange was warmly received in Paris, where
he had been preceded by his memoir on lunar libration. He may perhaps have been
treated too well in the Paris scientific community, where austerity was not a leading
virtue. Being of a delicate constitution, Lagrange fell ill and had to interrupt his
trip. In the spring of 1765 Lagrange returned to Turin by way of Geneva.
In the autumn of 1765 d´Alembert, who was on excellent terms with Frederick II
of Prussia, and familiar with Lagrange’s work through M´elanges de Turin, suggested
to Lagrange that he accept the vacant position in Berlin created by Euler’s departure
for St. Petersburg. It seems quite likely that Lagrange would gladly have remained
in Turin had the court of Turin been willing to improve his material and scientific
situation. On 26 April, d´Alembert transmitted to Lagrange the very precise and
advantageous propositions of the king of Prussia. Lagrange accepted the proposals
of the Prussian king and, not without difficulties, obtained his leave through the
intercession of Frederick II with the king of Sardinia. Eleven months after his arrival
in Berlin, Lagrange married his cousin Vittoria Conti who died in 1783 after a long
illness. With the death of Frederick II in August 1786 he also lost his strongest
support in Berlin. Advised of the situation, the princes of Italy zealously competed
in attracting him to their courts. In the meantime the French government decided
to bring Lagrange to Paris through an advantageous offer. Of all the candidates,
Paris was victorious.

744 Calculus of Variations
Lagrange left Berlin on 18 May 1787 to become pensionnaire v´et´eran of the Paris
Academy of Sciences, of which he had been a foreign associate member since 1772.
Warmly welcomed in Paris, he experiencedacertainlassitudeanddidnotimme-
diately resume his research. Yet he astonished those around him by his extensive
knowledge of metaphysics, history, religion, linguistics, medicine, and botany.
In 1792 Lagrange married the daughter of his colleague at the Academy, the
astronomer Pierre Charles Le Monnier. This was a troubled period, about a year
after the flight of the king and his arrest at Varennes. Nevertheless, on 3 June the
royal family signed the marriage contract “as a sign of its agreement to the union.”
Lagrange had no children from this second marriage, which, like the first, was a
happy one.
When the academy was suppressed in 1793, many noted scientists, including
Lavoisier, Laplace,andCoulomb were purged from its membership; but Lagrange
remained as its chairman. For the next ten years, Lagrange survived the turmoil of
the aftermath of the French Revolution, but by March of 1813, he became seriously
ill. He died on the morning of 11 April 1813, and three days later his body was
carried to the Panth´eon. The funeral oration was given by Laplace in the name of
the Senate.
30.2.2 Lagrangian Densities
Particles are localized objects (indeed mathematical points), whose trajecto-
ries, determined by ordinary differential equations, describe curves in space.
A Lagrangian of the form (30.40), with one independent variable (time), is
therefore appropriate for particles.
Most of physical quantities, however, are not particles, but fields, which
are not localized. In order to apply the variational techniques to fields, one has
to consider a Lagrangian density L, whose integral over some volume gives
the Lagrangian, which can now be integrated over time as in (30.2). Thus,
in field theories, the integration is over the 4-dimensional spacetime, a nat-
ural setting for relativity—which is very relevant because most field theories
are relativistic—to operate. A physical field usually has several components,
making Equation (30.23) relevant to the situation.
Electrodynamics Lagrangian
Section 17.3.2 derived the electromagnetic field tensor F
αβ
and wrote the four
Maxwell’s equations in terms of it. Since F
αβ
seems to be so fundamental,
and the variational techniques seem to yield the (partial) differential equations
of physics, there may be a chance that electrodynamics can be described by
a Lagrangian density. In the language of tensors, a Lagrangian density is a
scalar. Thus, we have to construct a scalar out of F
αβ
. The simplest such
scalar is F
αβ
F
αβ
. Equation (17.47) showed that the field tensor can be written
as derivatives of the 4-potential A
α
, which is therefore more “fundamental”
than F
αβ
. There is another 4-vector appearing in Maxwell’s equations, namely
the 4-current J
α
. Thus, by taking the dot product J
α
A
α
,weformanother
30.2 Lagrangian Dynamics 745
scalar. We therefore write
L = aF
αβ
F
αβ
+ bJ
α
A
α
= aη
αμ
η
βν
F
μν
F
αβ
+ bJ
α
A
α
,
where a and b are to be determined later. Writing the field tensor in terms of
the 4-potential, we get
L = aη
αμ
η
βν
(∂
μ
A
ν
− ∂
ν
A
μ
)(∂
α
A
β
− ∂
β
A
α
)+bJ
α
A
α
≡ aη
αμ
η
βν
(A
ν,μ
− A
μ,ν
)(A
β,α
− A
α,β
)+bJ
α
A
α
. (30.41)
The Euler-Lagrange equation for A
α
can be written as
∂L
∂A
σ
−
∂
∂x
ρ
∂L
∂A
σ,ρ
=0. (30.42)
The first term is easy to calculate:
∂L
∂A
σ
= bJ
α
∂A
α
∂A
σ
= bJ
α
δ
σ
α
= bJ
σ
.
The second term is only slightly more complicated once we realize that
∂A
β,α
∂A
σ,ρ
= δ
σ
β
δ
ρ
α
.
With this in mind, the second term of (30.42) can be shown to be
∂
∂x
ρ
∂L
∂A
σ,ρ
=4a∂
ρ
(∂
ρ
A
σ
− ∂
σ
A
ρ
)=4a∂
ρ
F
ρσ
,
and (30.42) becomes
4a∂
ρ
F
ρσ
= bJ
σ
or 4a∂
ρ
F
ρσ
= bJ
σ
.
This becomes Maxwell’s first and fourth equations combined [see Equation
(17.45)] if a =
1
4
and b = μ
0
. Thus the Lagrangian density for electrodynamics
is
L =
1
4
η
αμ
η
βν
(A
ν,μ
− A
μ,ν
)(A
β,α
− A
α,β
)+μ
0
J
α
A
α
. (30.43)
This, like any other Lagrangian, can be multiplied by a constant without
affecting the Euler-Lagrange equations.
Example 30.2.2.
ChargedParticleinEMField Problem 30.18 shows that
the Lagrangian density (30.43) can be written as
L =
1
2
|B|
2
−|E|
2
!
+ μ
0
(ρΦ − J · A) ,
with the variational problem
L =
#
b
a
##
Ω
L d
3
x
dt.

746 Calculus of Variations
Now consider a single particle of charge q interacting with an electromagnetic field.
For such a particle,
ρ = qδ(r − r
)andJ = ρv = qvδ(r − r
),
and L becomes
L =
1
2
#
b
a
dt
##
Ω
|B|
2
−|E|
2
!
d
3
x
+ μ
0
#
b
a
dt
##
Ω
qΦδ(r − r
) − qv · Aδ(r − r
)
!
d
3
x
=
1
2
#
b
a
dt
##
Ω
|B|
2
−|E|
2
!
d
3
x
+ μ
0
q
#
b
a
dt {Φ(r,t) − v ·A(r,t)}.
The particle also has kinetic energy, which needs to be added to this Lagrangian.
When adding Lagrangians, one has to incorporate the freedom in multiplying La-
grangians by constants. In the case at hand, the kinetic energy of the particle should
be added to the negative of the scalar potential energy (recall that L = KE − Φ).
To assure this, we have to divide the entire EM Lagrangian by −1/μ
0
and add it to
the kinetic energy of the particle. Hence the total Lagrangian becomes
L = −
1
2μ
0
#
b
a
dt
##
Ω
|B|
2
−|E|
2
!
d
3
x
+
#
b
a
dt
,
1
2
m|v|
2
− qΦ(r,t)+qv · A(r,t)
-
.
Notice how the first integral is four-dimensional while the second integral is over a
single variable.
We are interested in the motion of the particle. Therefore, the first integral
is just a constant (independent of the coordinates and velocity components of the
particle) and can be dropped. Thus, substituting
˙
r for v,wehave
L
part
=
#
b
a
dt
,
1
2
m|
˙
r|
2
− qΦ(r,t)+q
˙
r · A(r,t)
-
,
with the LagrangianLagrangian of a
charged particle in
EM field
L(r,
˙
r,t)=
1
2
m|
˙
r|
2
− qΦ(r,t)+q
˙
r · A(r,t). (30.44)
Let’s look at the x-component of the motion:
∂L
∂x
−
d
dt
∂L
∂ ˙x
=0 or − q
∂Φ
∂x
+ q
˙
r ·
∂A
∂x
−
d
dt
(m ˙x + qA
x
)=0,
or
m¨x + q
∂Φ
∂x
+ q
dA
x
dt
−
˙
r ·
∂A
∂x
=0. (30.45)
Now note that
dA
x
dt
=
∂A
x
∂t
+
∂A
x
∂x
˙x +
∂A
x
∂y
˙y +
∂A
x
∂z
˙z,
and
˙
r ·
∂A
∂x
=˙x
∂A
x
∂x
+˙y
∂A
y
∂x
+˙z
∂A
z
∂x
.
Putting these two equations in (30.45) and rearranging, we obtain
m¨x + q
∂Φ
∂x
+
∂A
x
∂t
=−E
x
by (15.31)
+q ˙y
∂A
x
∂y
−
∂A
y
∂x
=−B
z
by (15.31)
+q ˙z
∂A
x
∂z
−
∂A
z
∂x
=B
y
by (15.31)
=0,

30.3 Hamiltonian Dynamics 747
or
m¨x − qE
x
− q (˙yB
z
− ˙zB
y
)=0. (30.46)
The expression in parentheses is just the x-component of v×B. Thus, (30.46) is the
x-component of the Lorentz force law, governing the motion of a charged particle in
an electromagnetic field.
Klein-Gordon Lagrangian
One of the first attempts at combining the special theory of relativity with
quantum mechanics was made by Oskar Klein and Walter Gordon. In fact,
Schr
¨
dinger himself started with the relativistic version of his equation, but
abandoned it because of some difficulty he encountered when applying it to
hydrogen atom. By the usual substitution
E → i
∂
∂t
, p →−i∇
in the relativistic equation E
2
/c
2
− p · p = m
2
c
2
, Klein and Gordon derived
the equation that now bears their names:
1
c
2
∂
2
φ
∂t
2
−∇
2
φ +
m
2
c
2
2
φ =0,
which, in units =1=c, becomes
∂
2
φ
∂t
2
−∇
2
φ + m
2
φ =0.
This equation can also be obtained from the Lagrangian density
L = η
αβ
(∂
α
φ)(∂
β
φ) −
m
2
2
φ
2
, (30.47)
as the reader can verify.
30.3 Hamiltonian Dynamics
The Lagrangian formulation of mechanics treated in the previous section is a
powerful tool for studying many different dynamical systems and fields. Fur-
thermore, considerations of symmetry, an indispensable technique in the inves-
tigation of fundamental forces, is most adequately handled in the Lagrangian
language. Once the Lagrangian is known, the Euler-Lagrange equations pro-
vide second-order differential equations to be solved under given boundary (or
initial) conditions.
There is another formulation of mechanics, which instead of second-order
differential equations, yields twice as many first-order DEs. It is called the
Hamiltonian formulation. We describe only the case of several dependent
and one independent variables, the other cases being very similar. Let us

748 Calculus of Variations
assume that our dynamical system has n generalized coordinates {q
i
}
n
i=1
and
a Lagrangian L (q,
˙
q,t). In the simplest case (30.40), L = KE−ΦwhereKE
is a quadratic term in velocities alone and Φ dependent on the coordinates
alone. In such a case,
∂L
∂ ˙q
j
=
∂KE
∂ ˙q
j
= μ
j
˙q
j
,
which is the momentum associated with the jth generalized coordinate. It is
therefore natural to generalize the concept of momentum as well, write
p
j
≡
∂L(q,
˙
q,t)
∂ ˙q
j
, (30.48)
and call p
j
so defined the generalized momentum of the dynamical system.
The transition from Lagrangian to Hamiltonian formulation, from a strictly
mathematical standpoint, is to go from the set of variables (q,
˙
q,t)to(q, p,t).
The procedure for making this transition is the Legendre transformation dis-
cussed in Section 2.2.2. To find the variables involved, consider the differential
of the Lagrangian:
dL =
n
i=1
∂L
∂q
i
dq
i
+
∂L
∂ ˙q
i
d ˙q
i
+
∂L
∂t
dt,
and use (30.48) and the Euler-Laggrange equation to rewrite the above as
dL =
n
i=1
(˙p
i
dq
i
+ p
i
d ˙q
i
)+
∂L
∂t
dt.
If we want to switch the independent variable from ˙q
i
to p
i
,thenwehaveto
define the Hamiltonian as
H (q, p,t)=
n
i=1
p
i
˙q
i
− L (q,
˙
q,t) . (30.49)
Toverifythis,wenotethat
dH =
n
i=1
(˙q
i
dp
i
+ p
i
d ˙q
i
)−dL=
n
i=1
(˙q
i
dp
i
+ p
i
d ˙q
i
)−
n
i=1
(˙p
i
dq
i
+ p
i
d ˙q
i
)−
∂L
∂t
dt.
Note that p
i
d ˙q
i
terms cancel and we are left with
dH =
n
i=1
(˙q
i
dp
i
− ˙p
i
dq
i
) −
∂L
∂t
dt.
On the other hand,
dH =
n
i=1
∂H
∂q
i
dq
i
+
∂H
∂p
i
dp
i
+
∂H
∂t
dt.
30.3 Hamiltonian Dynamics 749
Comparison of the last two equations gives
˙q
i
=
∂H
∂p
i
, ˙p
i
= −
∂H
∂q
i
, −
∂L
∂t
=
∂H
∂t
,i=1, 2,...,n, (30.50)
which are called Hamilton or canonical equations. Note that instead of n
second-order DEs, we now have 2n first order DEs.
To discover the physical significance of the Hamiltonian, consider the fa-
miliar simple Lagrangian L = KE −Φ, where KE is the usual kinetic energy
term and Φ is the potential energy which is independent of velocities. Then,
(30.48) yields p
i
= μ
i
˙q
i
and Hamiltonian is the
total energy.
H =
n
i=1
p
i
˙q
i
− L =
n
i=1
μ
i
˙q
2
i
=2KE
−KE +Φ=KE +Φ.
So H is the sum of the kinetic and potential energies, i.e., the total energy.
Example 30.3.1.
Hamiltonian of a Charged Particle in EM Field The
Lagrangian of a charged particle in an electromagnetic field is given by (30.44).
Let’s find the Hamiltonian of this system. First we need the generalized momentum
(30.48):
p
i
=
∂L
∂ ˙x
i
= m ˙x
i
+ qA
i
or p = m
˙
r + qA. (30.51)
This is an important equation in its own right. It says that the momentum of the
system is not just that of the particle, but that it also includes a contribution from
the EM field. In particular, that EM field has momentum.
1
To find the Hamiltonian, compute
˙
r from (30.51):
˙
r =
p − qA
m
,
and substitute in the definition of the Hamiltonian (30.49), where, in this case the
sum is just the dot product:
H(r, p,t)=p ·
p − qA
m
−
1
2
m
p − qA
m
2
+ qΦ − q
p − qA
m
· A
=(p − qA) ·
p − qA
m
−
1
2
|p − qA|
2
m
+ qΦ,
or
H(r, p,t)=
|p − qA(r,t)|
2
2m
+ qΦ(r,t). (30.52)
Thus, in the presence of an electromagnetic field, the Hamiltonian of a particle takes
the same form as the total energy of a particle in a potential qΦ, except that in the
expression for the KE part, p − qA replaces p. Such a replacement is called the
minimal coupling and plays a key role in the quantum mechanical treatment of
charged particles interacting with EM fields.
1
This momentum is the source of radiation pressure.

750 Calculus of Variations
30.4 Problems
30.1. Show that, in Example 30.1.6, C
1
=0,λ = λ
0
,andC
2
=
λ
2
0
− a
2
,
where λ
0
is the solution of the equation
λ sin
l
2λ
= a.
30.2. Find the extremal of the functional
L[x, y]=
#
π/2
0
(˙x
2
+˙y
2
+2xy) dt
subject to the boundary conditions
x(0) = 0,x(π/2) = 1,y(0) = 0,y(π/2) = 1.
30.3. Find the extremals of the following functionals:
(a) L[x, y]=
#
b
a
(˙x
2
+˙y
2
+˙x ˙y) dt, (b) L[x, y]=
#
b
a
(2xy − 2x
2
+˙x
2
− ˙y
2
) dt.
30.4. Find the extremal of a functional of the form
L[x, y]=
#
b
a
L(˙x, ˙y) dt,
given that
∂
2
L
∂ ˙x
2
∂
2
L
∂ ˙y
2
−
∂
2
L
∂ ˙x∂ ˙y
2
=0fora ≤ x ≤ b.
30.5. Find the extremal of the functional
L[x]=
#
1
0
(˙x
2
+ t
2
) dt,
subject to the boundary conditions
x(0) = 0,x(1) = 0,
#
1
0
x
2
dt =2.
30.6. Show that the extremization of (30.33) leads to the Euler-Lagrange
equations (30.34).
30.7. Among all triangles with a given base line and a fixed perimeter, show
that the isosceles triangle has the largest area.
30.8. An airplane with fixed air speed v
0
flies for a time T on a closed curve.
The wind velocity u is constant in magnitude and direction and |u| <v
0
.
What closed curve encloses the largest area?
