Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

18.2 Polar Form of Complex Numbers 483
because i
2k
=(i
2
)
k
=(−1)
k
. This is probably the most important relation in
complex number theory.
Box 18.2.1. The trigonometric and imaginary exponential functions are
related by the Euler equation: e
iθ
=cosθ + i sin θ.
The use of Equation (18.11) in (18.10) leads to another way of representing
complex numbers:
z = re
iθ
,r=
x
2
+ y
2
,θ=tan
−1
y
x
. (18.12)
Note that
Box 18.2.2. The angle θ is not uniquely determined: Any multiple of 2π
can be added to it without affecting z.
We can use Equation (18.12) together with x = r cos θ, y = r sin θ to con-
vert from Cartesian coordinates to polar coordinates, and vice versa. The
coordinate θ is called the argument of z and written θ =arg(z).
argument of a
complex number
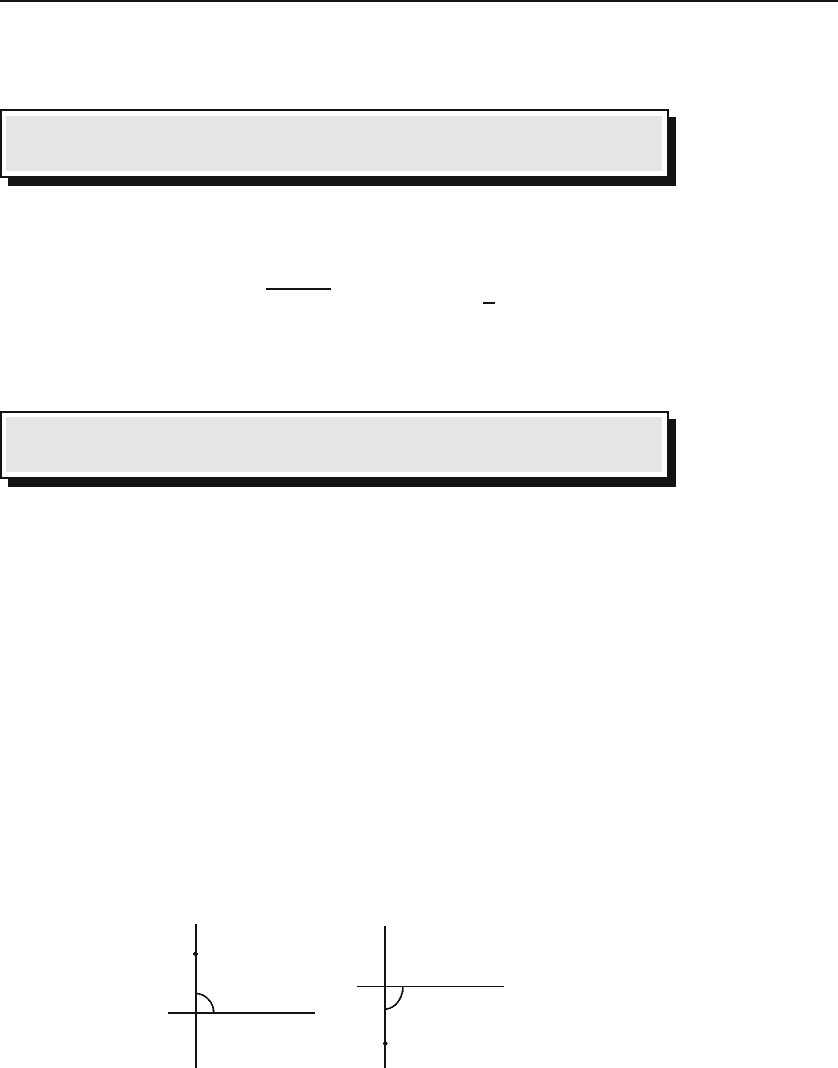
Example 18.2.1. Let us look at some numerical examples of polar-Cartesian
conversion. In many cases, a diagram can be very helpful. For instance, take i
whose real part is obviously zero and whose imaginary part is 1. If we were to use
the formula, we would have tan θ =1/0 which is not defined. However, Figure 18.4
shows that z = i lies on the positive imaginary axis, and, thus, θ = π/2. Since we
can always add a multiple of 2π to the angle, we have
i = e
iπ/2+i2nπ
,n=0, ±1, ±2,....
Similarly, the same figure makes it clear that
−i = e
−iπ/2+i2nπ
= e
i3π/2+i2nπ
,n=0, ±1, ±2,....
θ = π/2
r 1
=
i
Re
Im
θ = − π/2
Re
Im
−i
r 1=
Figure 18.4: Cartesian and polar coordinates for i and −i.
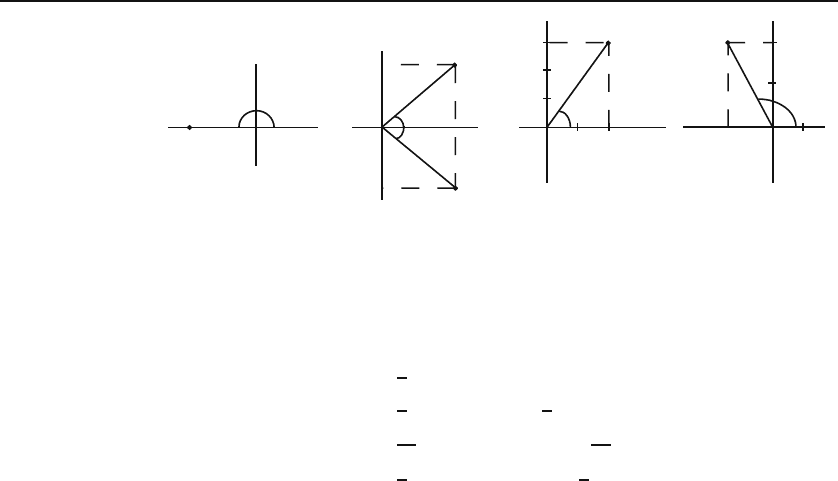
484 Complex Arithmetic
Re
θ = π
r = 1
Im
−1
θ = π/4
Re
Im
1+ i
1− i
θ = − π/4
θ
Re
Im
2 + i3
θ
Re
Im
−1 + i2
Figure 18.5: Cartesian and polar coordinates for some other complex numbers.
Referring to Figure 18.5, the reader may verify the following polar representa-
tions of complex numbers:
−1=e
iπ+i2nπ
,
1+i =
√
2 e
iπ/4+i2nπ
,
1 − i =
√
2 e
−iπ/4+i2nπ
=
√
2 e
i7π/4+i2nπ
,
2+i3=
√
13 e
i tan
−1
(3/2)+i2nπ
=
√
13 e
i0.983+i2nπ
,
−1+i2=
√
5 e
i tan
−1
(−2)+i2nπ
=
√
5 e
i2.03+i2nπ
.
In all cases, n is an integer and angles are in radians.
The complex conjugate of z in polar coordinates is
z
∗
= x − iy = r cos θ − ir sin θ = r cos(−θ)+ir sin(−θ)=re
−iθ
.
This equation confirms the earlier statement that complex conjugation is
equivalent to replacing i with −i.
Generally speaking, polar coordinates are useful for operations of multipli-
cation, division, and exponentiation, and Cartesian coordinates for addition
and subtraction.
Example 18.2.2.
We can use the polar representation of complex numbers to
find some trigonometric identities. In all of the following, we set r =1:
1=e
iθ
e
−iθ
=(cosθ + i sin θ)(cos θ − i sin θ)=cos
2
θ +sin
2
θ.
Now consider the identity
e
i(θ
1
+θ
2
)
=cos(θ
1
+ θ
2
)+i sin(θ
1
+ θ
2
)
which can also be written as
e
i(θ
1
+θ
2
)
= e
iθ
1
e
iθ
2
=(cosθ
1
+ i sin θ
1
)(cos θ
2
+ i sin θ
2
)
=cosθ
1
cos θ
2
− sin θ
1
sin θ
2
+ i(sin θ
1
cos θ
2
+sinθ
2
cos θ
1
).
Equating the real and imaginary parts of the last two equations, we obtain
cos(θ
1
+ θ
2
)=cosθ
1
cos θ
2
− sin θ
1
sin θ
2
,
sin(θ
1
+ θ
2
)=sinθ
1
cos θ
2
+sinθ
2
cos θ
1
.

18.2 Polar Form of Complex Numbers 485
Similarly, equating the real and imaginary parts of
e
i3θ
=cos3θ + i sin 3θ
and
e
i3θ
=
e
iθ
3
=(cosθ + i sin θ)
3
=cos
3
θ +3i cos
2
θ sin θ − 3sin
2
θ cos θ −i sin
3
θ
gives the following trigonometric identity:
cos 3θ =4cos
3
θ −3cosθ,
sin 3θ =3sinθ − 4sin
3
θ.
From
e
inθ
=cosnθ + i sin nθ and e
inθ
=(e
iθ
)
n
=(cosθ + i sin θ)
n
we obtain the so-called de Moivre theorem: de Moivre theorem
(cos θ + i sin θ)
n
=cosnθ + i sin nθ. (18.13)
Equation (18.11) and its complex conjugate lead to the following useful
results:
two important
relations
cos θ =
1
2
e
iθ
+ e
−iθ
!
,
sin θ =
1
2i
e
iθ
− e
−iθ
!
. (18.14)
As mentioned earlier, the exponential nature of polar coordinates makes
them especially useful in multiplication, division, and exponentiation. For
instance,
z
1
z
2
=
r
1
e
iθ
1
r
2
e
iθ
2
=
r
1
r
2
e
i(θ
1
−θ
2
)
,
z
1
z
2
=
r
1
e
iθ
1
!
r
2
e
iθ
2
!
= r
1
r
2
e
i(θ
1
+θ
2
)
, (18.15)
√
z =
√
re
iθ
=
re
iθ
!
1/2
= r
1/2
e
iθ
!
1/2
=
√
re
iθ/2
,
and so forth.
All of these relations have interesting geometric interpretations. For ex-
ample, the second equation says that when you multiply a complex number z
1
by another complex number z
2
, you dilate the magnitude of z
1
by a factor r
2
and increase its angle by θ
2
. That is, multiplication involves both a dilation
and a rotation. In particular, if we multiply a complex number by e
iωt
where
t is time, we get a vector of constant length in the xy-plane that is rotating
with angular velocity ω.
Example 18.2.3.
A plane wave is represented by a periodic function such as
A cos(kx − ωt)orB sin(kx − ωt).

486 Complex Arithmetic
On the other hand, sine and cosine are related by
sin(kx − ωt)=−cos
kx − ωt +
π
2
.
Therefore, one can concentrate solely on the cosine function with a phase an-
gle added to its argument. Thus a typical periodic plane wave is represented as
A cos (kx − ωt + α). To make connection with the material of this section, we note
that
A cos (kx − ωt + α)=A Re
e
i(kx−ωt+α)
=Re
Ae
i(kx−ωt+α)
=Re
Ae
iα
e
i(kx−ωt)
=Re
Ze
i(kx−ωt)
,
where Z is a complex number—called complex amplitude—of magnitude A andcomplex amplitude
argument α. It is therefore convenient to represent plane waves by the complex
function Ze
i(kx−ωt)
which includes the phase of the wave as the argument of Z.
Another interesting application of these ideas is finding roots of complex
numbers. Suppose we are interested in all the nth roots of Z; i.e., all z’s
roots of complex
numbers
satisfying z
n
= Z. To find the roots of a complex number Z, write it in polar
form in the most general way:
Z = Re
iΘ+i2πk
,k=0, ±1, ±2,...,
Thus,
z
n
= Re
iΘ+i2πk
with k =0, ±1, ±2,....
Taking the nth root of both sides, we obtain
z = Z
1/n
= R
1/n
e
iΘ/n+i2πk/n
,k=0, ±1, ±2,...,
and
Box 18.2.3. The distinct nth roots {z
k
} of Z = Re
iΘ
are
z
k
= R
1/n
e
iΘ/n+i2πk/n
,k=0, 1, 2,..., n−1. (18.16)
We see that the number of nth roots of a complex number is exactly n.
It is clear that z
k
of Equation (18.16) repeats itself for k ≥ n.
Example 18.2.4.
Let us find the three cube roots of unity. With n =3and
Z = e
i2πk
,wehave
z
k
= e
i2πk/3
,k=0, 1, 2,
or
z
0
= e
0
=1,
z
1
= e
i2π/3
=cos
2π
3
+ i sin
2π
3
= −
1
2
+ i
√
3
2
,
z
2
= e
i4π/3
=cos
4π
3
+ i sin
4π
3
= −
1
2
− i
√
3
2
.
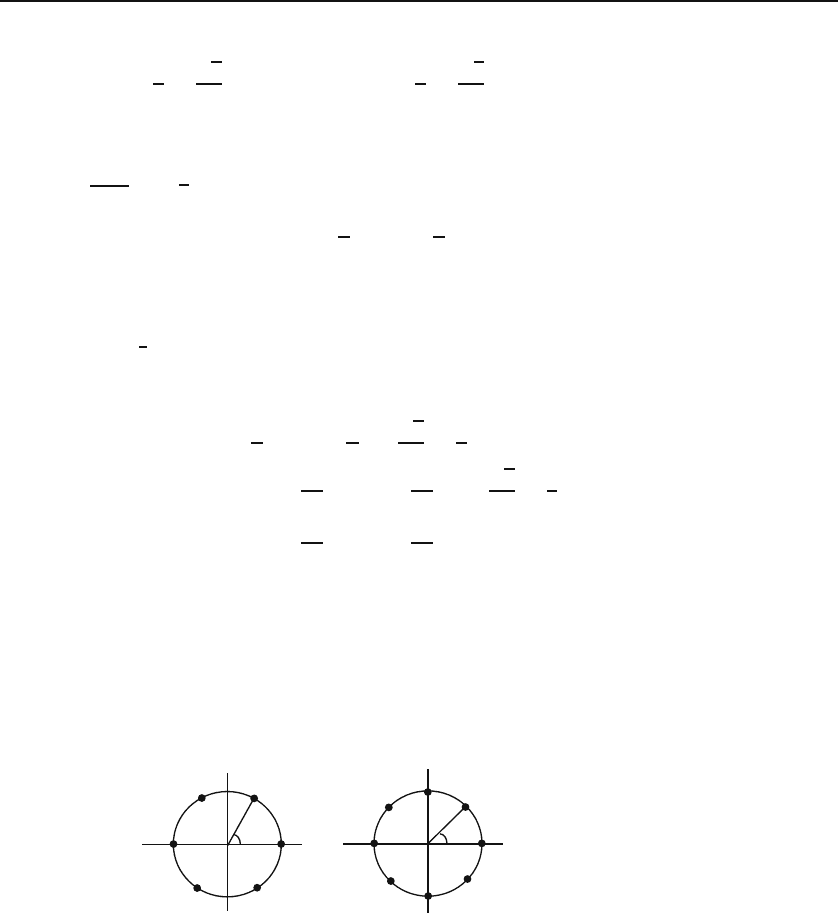
18.2 Polar Form of Complex Numbers 487
It is instructive to show directly that
−
1
2
+ i
√
3
2
3
=1 and
−
1
2
− i
√
3
2
3
=1.
Here are some more examples of finding roots:
√
1+i =
√
2 e
iπ/4+i2nπ
1/2
=2
1/4
e
iπ/8+inπ
n =0, 1,
z
0
=2
1/4
e
iπ/8
=2
1/4
3
cos
π
8
+ i sin
π
8
4
=1.1+i0.456,
z
1
=2
1/4
e
iπ/8+iπ
= −2
1/4
e
iπ/8
= −1.1 − i0.456.
The equation z
3
= i has the roots
3
√
i =
e
iπ/2+i2nπ
1/3
= e
iπ/6+i2nπ/3
,n=0, 1, 2,
or
z
0
= e
iπ/6
=cos
π
6
+ i sin
π
6
=
√
3
2
+ i
1
2
,
z
1
= e
iπ/6+i2π/3
=cos
5π
6
+ i sin
5π
6
= −
√
3
2
+ i
1
2
,
z
2
= e
iπ/6+i4π/3
=cos
3π
2
+ i sin
3π
2
= −i.
The reader is urged to show that z
3
k
= i for k =0, 1, 2.
Note how careful we were to include the factor of e
i2nπ
when taking roots of
complex numbers.
All nth roots of Z = Re
iΘ
are equally spaced on a circle of radius R
1/n
in
the complex plane. Figure 18.6 shows two circles on which the sixth and the
eighth roots of unity are located.
π/4
Re
π/3
Re
Im
Im
(a)
(b)
Figure 18.6: The (a) sixth and (b) eighth roots of unity.
Example 18.2.5. In certain applications of electromagnetic wave propagation (as Cartesian form of
the square root of
a complex number
in conductors) it becomes necessary to find an analytic expression for the Cartesian
representation of the square root of a complex number. In this example, we derive
such an expression.
488 Complex Arithmetic
We are trying to calculate the Cartesian representation of the square root of
z = x + iy. First we express z in polar form; next we take its square root, and
finally reexpress the result in Cartesian form. Thus,
z = re
i(θ+2nπ)
where r =
x
2
+ y
2
, tan θ =
y
x
,n=0, ±1, ±2,....
Taking the square root of both sides yields
√
z = z
1/2
= r
1/2
e
i(θ+2nπ)/2
=(x
2
+ y
2
)
1/4
e
iθ/2+inπ
= ±(x
2
+ y
2
)
1/4
e
iθ/2
= ±(x
2
+ y
2
)
1/4
cos
θ
2
+ i sin
θ
2
because e
inπ
=1ifn is even and e
inπ
= −1ifn is odd. All that is left now is to
express the trigonometric functions in terms of x and y:
cos
θ
2
=
.
1
2
(1 + cos θ)
/
1/2
=
1
√
2
1+
1
√
1+tan
2
θ
1/2
=
1
√
2
1+
1
1+(y/x)
2
1/2
=
1
√
2
1+
|x|
x
2
+ y
2
1/2
.
Similarly,
sin
θ
2
=
1
√
2
1 −
|x|
x
2
+ y
2
1/2
.
Collecting all these formulas together and simplifying, we obtain
x + iy = ±
1
√
2
x
2
+ y
2
+ |x|
1/2
+ i
x
2
+ y
2
−|x|
1/2
. (18.17)
The complexity of the expression for the square root rests on our insistence on
an analytic form. The process of converting the Cartesian form of a complex number
to polar, taking the square root, and converting the result back to Cartesian form
is a far easier process than the one leading to Equation (18.17).
18.3 Fourier Series Revisited
The connection between the trigonometric and exponential functions can be
utilized to write the Fourier series expansion of periodic functions more suc-
cinctly. If we substitute
cos
2nπx
L
=
e
2inπx/L
+ e
−2inπx/L
2
,
sin
2nπx
L
=
e
2inπx/L
− e
−2inπx/L
2i
,
in Equation (10.38) and collect the similar exponential terms, we obtain
f(x)=a
0
+
1
2
∞
n=1
*
(a
n
− ib
n
) e
2inπx/L
+(a
n
+ ib
n
) e
−2inπx/L
+
= a
0
+
1
2
∞
n=1
(a
n
− ib
n
) e
2inπx/L
+
1
2
∞
n=1
(a
n
+ ib
n
) e
−2inπx/L
. (18.18)
18.3 Fourier Series Revisited 489
In the second sum, let n = −m to obtain
2nd sum =
1
2
−∞
m=−1
(a
−m
+ ib
−m
) e
2imπx/L
=
1
2
−∞
n=−1
(a
−n
+ ib
−n
) e
2inπx/L
,
(18.19)
where in the last step, we switched the dummy index back to n.Ifwenow
introduce new coefficients A
n
defined as
A
n
=
⎧
⎪
⎨
⎪
⎩
1
2
(a
n
− ib
n
)if1≤ n ≤∞,
1
2
(a
−n
+ ib
−n
)if −∞≤n ≤−1,
a
0
if n =0,
and use Equation (18.19) in (18.18), we obtain
Fourier series in
terms of complex
exponentials
f(x)=
+∞
n=−∞
A
n
e
2inπx/L
where L = b − a, (18.20)
which is the equation we are after. To find A
n
directly from this equation,
multiply both sides by e
−2ikπx/L
,integratefroma to b, and use the readily
obtainable relation
#
b
a
e
2i(n−k)πx/L
=
0
0ifn = k
L if n = k
= Lδ
nk
, (18.21)
where δ
nk
is the Kronecker delta. It follows that
A
k
=
1
L
#
b
a
f(x)e
−2ikπx/L
dx or A
n
=
1
L
#
b
a
f(x)e
−2inπx/L
dx. (18.22)
It is customary to redefine the coefficients in the summation of Equation
(18.20) in such a way that the summation giving f(x) and the integral giving
A
n
are more symmetric, i.e., have the same constant in front of them. To this
end, define f
n
≡
√
LA
n
. Then (18.20) and (18.22) become
f(x)=
1
√
L
+∞
n=−∞
f
n
e
2inπx/L
,f
n
=
1
√
L
#
b
a
f(x)e
−2inπx/L
dx (18.23)
Note that the coefficients f
n
are complex; however, when f(x)isareal
function, the exponentials and their complex coefficients add up in such a
way that the final result can be expressed as an infinite sum of trigonometric
functions with real coefficients. In fact, we can show this generally using
Equations (18.23). First, we note that, for real f(x),
f
∗
n
=
1
√
L
#
b
a
f(x)e
+2inπx/L
dx =
1
√
L
#
b
a
f(x)e
−2i(−n)πx/L
dx = f
−n
.
(18.24)

490 Complex Arithmetic
Next, we split the sum in (18.23) into positive integers, negative integers, and
zero:
f(x)=
1
√
L
−1
n=−∞
f
n
e
2inπx/L
+
f
0
√
L
+
1
√
L
∞
n=1
f
n
e
2inπx/L
. (18.25)
Changing the dummy index n to −m, the first sum can be rewritten as
1st sum =
1
√
L
−1
−m=−∞
f
−m
e
−2imπx/L
=
1
√
L
∞
m=1
f
−m
e
−2imπx/L
=
1
√
L
∞
m=1
f
∗
m
e
−2imπx/L
=
1
√
L
∞
n=1
f
∗
n
e
−2inπx/L
,
where we used Equation (18.24) and changed m back to n at the end. Sub-
stituting the last equation in (18.25) yields
f(x)=
f
0
√
L
+
1
√
L
∞
n=1
f
∗
n
e
−2inπx/L
+ f
n
e
2inπx/L
=
f
0
√
L
+
2
√
L
∞
n=1
Re
f
n
e
2inπx/L
showing that f(x) is indeed real. Equation (18.23) implies that f
0
is also real
when f (x) is. It is not hard to show that the expression in the parentheses of
the first line is the sum of a sine and a cosine with real coefficients.
Example 18.3.1.
Let us redo the square potential—whose Fourier series was
calculated in Example 10.6.1—using exponentials. From Equation (18.23), for n =0,
we obtain
f
n
=
1
√
2T
#
2T
0
V (t)e
−2inπt/(2T )
dt =
1
√
2T
#
T
0
V
0
e
−inπt/T
dt
=
V
0
√
2T
T
−inπ
e
−inπt/T
T
0
=
T
2
V
0
inπ
[1 − (−1)
n
]
because e
inπ
=(e
iπ
)
n
=(−1)
n
. Similarly, f
0
= V
0
T/2. We now substitute these
in the Fourier series expansion
V (t)=
1
√
2T
+∞
n=−∞
f
n
e
2inπt/2T
to get
V (t)=
V
0
2
+
−1
n=−∞
V
0
2inπ
[1 − (−1)
n
]e
2inπt/2T
+
∞
n=1
V
0
2inπ
[1 − (−1)
n
]e
2inπt/2T
.
18.4 A Representation of Delta Function 491
If we change the dummy index of the first sum from n to −m, and back to n again,
and put the two sums together, we obtain
V (t)=
V
0
2
+
∞
n=1
V
0
2inπ
[1 − (−1)
n
]
e
inπt/T
− e
−inπt/T
=
V
0
2
+
2V
0
π
∞
n=odd
1
2in
e
inπt/T
− e
−inπt/T
=2i sin(nπt/T )
=
V
0
2
+
2V
0
π
∞
k=0
sin[(2k +1)πt/T ]
2k +1
,
which is the expansion we obtained in Example 10.6.1 using trigonometric
functions.
18.4 A Representation of Delta Function
Consider the function D
T
(x − x
0
) defined as
D
T
(x −x
0
) ≡
1
2π
#
T
−T
e
i(x−x
0
)t
dt. (18.26)
The integral is easily evaluated, with the result
D
T
(x − x
0
)=
1
2π
e
i(x−x
0
)t
i(x − x
0
)
T
−T
=
1
π
sin T (x − x
0
)
x − x
0
.
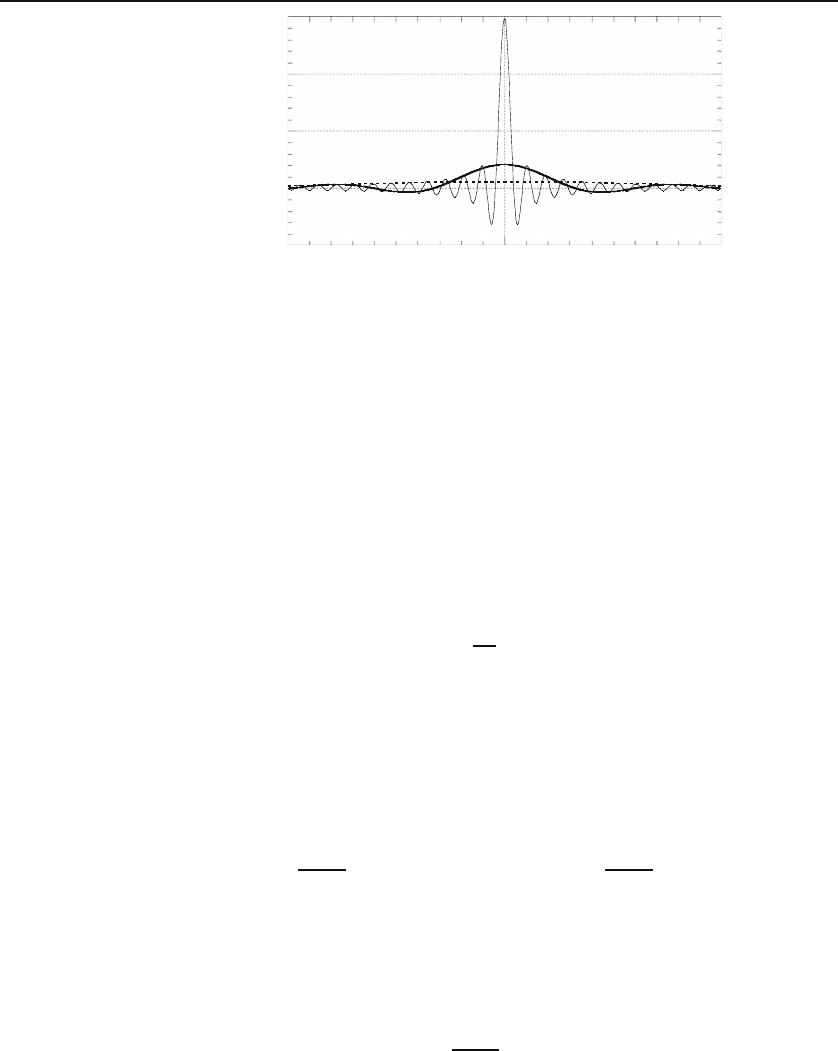
The graph of D
T
(x) as a function of x for various values of T is shown in
Figure 18.7. Note that the width of the curve decreases as T increases. The
area under the curve can be calculated:
#
∞
−∞
D
T
(x − x
0
) dx =
1
π
#
∞
−∞
sin T (x − x
0
)
x − x
0
dx =
1
π
#
∞
−∞
sin y
y
dy
=π
=1.
Figure 18.7 shows that D
T
(x −x
0
) becomes more and more like the Dirac
delta function as T gets larger and larger. In fact, we have
δ(x −x
0
) = lim
T →∞
D
T
(x − x
0
) = lim
T →∞
1
π
sin T (x − x
0
)
x − x
0
. (18.27)
To see this, we note that for any finite T we can write
D
T
(x −x
0
)=
T
π
sin T (x − x
0
)
T (x − x
0
)
.
Furthermore, for values of x that are very close to x
0
,
T (x − x
0
) → 0and
sin T (x − x
0
)
T (x − x
0
)
→ 1.
492 Complex Arithmetic
–5
50
Figure 18.7: The function sin Tx/x also approaches the Dirac delta function
as the width of the curve approaches zero. The value of T is 0.5 for the dashed
curve, 2 for the heavy curve, and 15 for the light curve.
Thus, for such values of x and x
0
,wehaveD
T
(x − x
0
) ≈ (T/π), which is
large when T is large. This is as expected of a delta function: δ(0) = ∞.On
the other hand, the width of D
T
(x − x
0
) around x
0
is given, roughly, by the
distance between the points at which D
T
(x −x
0
) drops to zero: T (x −x
0
)=
±π,orx − x
0
= ±π/T. This width is roughly Δx =2π/T,whichgoesto
zero as T grows. Again, this is as expected of the delta function. Therefore,
from (18.26) and (18.27), we have the following important representation of
the Dirac delta function:
delta function as
integral of
imaginary
exponential
δ(x −x
0
)=
1
2π
#
∞
−∞
e
i(x−x
0
)t
dt. (18.28)
Equation (18.28) can be generalized to higher dimensions, because (at least
in Cartesian coordinates) the multi-dimensional Dirac delta function is just
the product of the one-dimenstional delta functions. Using the more common
k instead of t as the variable of integration, the two-dimensional Dirac delta
function can be represented as
δ(r −r
0
)=
1
(2π)
2
#
∞
−∞
#
∞
−∞
e
ik·(r−r
0
)
dk
x
dk
y
≡
1
(2π)
2
##
Ω
∞
e
ik·(r−r
0
)
d
2
k,
(18.29)
where Ω
∞
means over all k
x
k
y
-plane and in the last integral we substituted
d
2
k for dk
x
dk
y
.
Similarly, the three dimensional Dirac delta function has the following
representation:
δ(r −r
0
)=
1
(2π)
3
##
Ω
∞
e
ik·(r−r
0
)
d
3
k, (18.30)
where d
3
k means a triple integral over k and Ω
∞
means over all k-space.
