Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


462 Tensor Anal ysi s
17.4 Differentiation of Tensors
Tensors represent many quantities, whose variation with coordinates (points
in space) has physical significance. Therefore, the notion of a derivative of a
tensor becomes important. Although we can always differentiate components
of a tensor (they are just functions), the resulting derivative is not necessarily
a tensor. To obtain a tensor, one needs to generalize the concept of the
derivative, as we do in this section.
17.4.1 Covariant Differential and Affine Connection
Let us begin by noting that the differentials of coordinates form the com-
ponents of a contravariant vector. In fact, when the new coordinates ¯x
i
are
written as functions of the old coordinates x
j
and one takes the differential
of the new coordinates, one obtains
d¯x
i
=
∂¯x
i
∂x
j
dx
j
, (17.49)
which is precisely the way a contravariant vector transforms. In fact, this
is the archetypal example of a contravariant vector, and can be a guide in
helping the reader remember the rule of transformation of the contravariant
components of a tensor.
The differential of a scalar—a tensor of type (0, 0)—is again a scalar,
because
dφ =
∂φ
∂x
i
dx
i
,
and the first term is the components of a covariant vector [see Equation
(17.15)], and the second term the components of a covariant vector (as shown
above).
Next take the differential of a contravariant vector A
i
.Howdoesittrans-
form? By taking the differential of the transformation rule
¯
A
i
=
∂¯x
i
∂x
j
A
j
, (17.50)
one obtains
d
¯
A
i
=
∂¯x
i
∂x
j
dA
j
+ d
∂¯x
i
∂x
j
A
j
=
∂¯x
i
∂x
j
dA
j
+
∂
2
¯x
i
∂x
k
∂x
j
dx
k
A
j
. (17.51)
If the second term on the right were absent, dA
j
would transform as a con-
travariant vector. It turns out that one can add something to dA
j
whose effect
is to cancel the unwanted term.
Consider quantities Γ
j
mp
, which transform according tocomponents of
affine connection
Γ
j
mp
=
∂¯x
j
∂x
l
∂x
h
∂¯x
m
∂x
k
∂¯x
p
Γ
l
hk
−
∂
2
¯x
j
∂x
h
∂x
k
∂x
h
∂¯x
m
∂x
k
∂¯x
p
. (17.52)
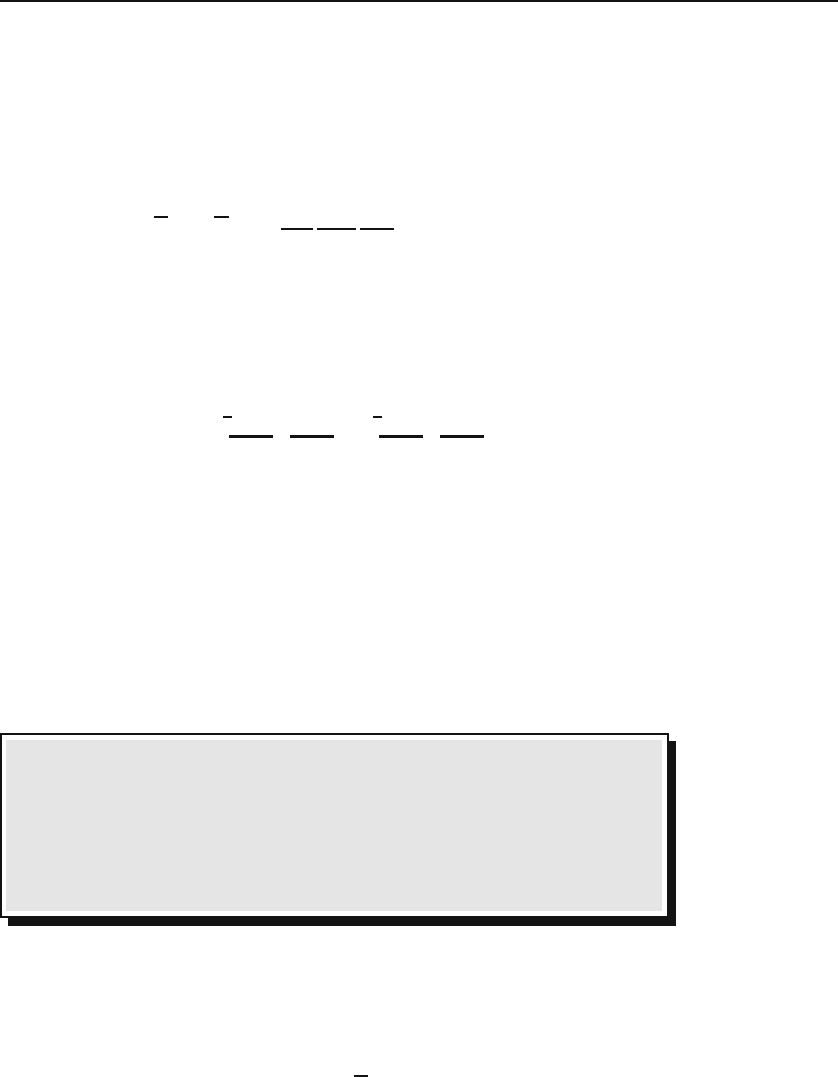
17.4 Differentiation of Tensors 463
Any set of three-indexed symbols Γ
j
mp
which transform according to this equa-
tion is said to constitute the components of an affine connection.Anaffine
connection is not a tensor because of the second term on the right-hand side
of (17.52). Since this term is the same for all affine connections, the difference
between two affine connections is a tensor of type (1, 2). If Γ
j
mp
and Λ
j
mp
are
any two affine connections then
Γ
j
mp
− Λ
j
mp
=
∂¯x
j
∂x
l
∂x
h
∂¯x
m
∂x
k
∂¯x
p
Γ
l
hk
− Λ
l
hk
!
, (17.53)
showing that Γ
l
hk
− Λ
l
hk
transform as components of a tensor of type (1, 2).
In particular, if Λ
l
hk
=Γ
l
kh
, then the difference Γ
l
hk
− Γ
l
kh
is essentially the
antisymmetric part of the affine connection Γ:
Γ
l
hk
=
1
2
Γ
l
hk
+Γ
l
kh
!
symmetric part
+
1
2
Γ
l
hk
− Γ
l
kh
!
antisymmetric part
.
The antisymmetric part of an affine connection is called its torsion ten-
torsion tensor
sor. Clearly if it vanishes in one coordinate system then it vanishes in all
coordinates (the zero tensor is zero in all coordinate systems). Thus, the
torsion tensor of an affine connection is zero, if an only if the connection is
symmetric.
Lack of tensorial character of the affine connection is precisely what is
needed to make dA
j
,aswellasdA
j
atensor:
Box 17.4.1. For any affine connection Γ
j
kl
, the quantities DA
j
and DA
j
defined by
DA
j
= dA
j
+Γ
j
kl
A
k
dx
l
and DA
j
= dA
j
− Γ
k
jl
A
k
dx
l
are, respectively, the components of a contravariant and a covariant vec-
tor. They are called the covariant or absolute differential of the vectors.
We show that DA
j
is a contravariant vector, leaving the proof of the second
claim to the reader. In the bar coordinates, we have
D
¯
A
j
= d
¯
A
j
+ Γ
j
kl
¯
A
k
d¯x
l
.

464 Tensor Anal ysi s
Using Equations (17.49), (17.50), (17.51), and (17.52), we obtain
D
¯
A
j
=
∂¯x
j
∂x
k
dA
k
+
∂
2
¯x
j
∂x
k
∂x
l
dx
k
A
l
+
∂¯x
j
∂x
p
∂x
q
∂¯x
k
∂x
r
∂¯x
l
Γ
p
qr
−
∂
2
¯x
j
∂x
q
∂x
r
∂x
q
∂¯x
k
∂x
r
∂¯x
l
∂¯x
k
∂x
m
A
m
∂¯x
l
∂x
s
dx
s
=
∂¯x
j
∂x
k
dA
k
+
∂
2
¯x
j
∂x
k
∂x
l
dx
k
A
l
+
∂¯x
j
∂x
p
∂x
q
∂¯x
k
∂¯x
k
∂x
m
=δ
q
m
∂x
r
∂¯x
l
∂¯x
l
∂x
s
=δ
r
s
Γ
p
qr
A
m
dx
s
−
∂
2
¯x
j
∂x
q
∂x
r
∂x
q
∂¯x
k
∂¯x
k
∂x
m
=δ
q
m
∂x
r
∂¯x
l
∂¯x
l
∂x
s
=δ
r
s
A
m
dx
s
=
∂¯x
j
∂x
k
dA
k
+
∂
2
¯x
j
∂x
k
∂x
l
dx
k
A
l
+
∂¯x
j
∂x
p
Γ
p
qr
A
q
dx
r
−
∂
2
¯x
j
∂x
q
∂x
r
A
q
dx
r
.
The second term cancels the last term (remember that you can use any symbol
for the dummy indices that are summed over). Therefore,
D
¯
A
j
=
∂¯x
j
∂x
k
dA
k
+
∂¯x
j
∂x
p
Γ
p
qr
A
q
dx
r
=
∂¯x
j
∂x
k
dA
k
+
∂¯x
j
∂x
k
Γ
k
qr
A
q
dx
r
=
∂¯x
j
∂x
k
dA
k
+Γ
k
qr
A
q
dx
r
!
=
∂¯x
j
∂x
k
DA
k
,
which is the transformation rule of a contravariant vector.
Absolute differential can be defined for any tensor. For a scalar φ, Dφ =
dφ. In the case of other tensors, for each contravariant index an affine con-
nection term with a positive sign, and for each covariant index an affine con-
nection term with a negative sign is introduced. For example, the covariant
differential of T
ij
k
is a tensor of type (2, 1) given by
DT
ij
k
= dT
ij
k
+
Γ
i
pq
T
pj
k
+Γ
j
pq
T
ip
k
− Γ
p
kq
T
ij
p
dx
q
.
Covariant differential has all the properties of ordinary differential when ap-
plied to tensors. For example, the covariant differential of the sum of two
tensors of type (r, s) is a tensor of type (r, s), and D(αT)=αDT for any
constant α and any tensor T. Covariant differential also obeys the Leibniz
rule:
D(T ⊗ S)=DT ⊗S + T ⊗DS. (17.54)
17.4.2 Covariant Derivative
In the first equation of Box 17.4.1, write dA
j
in terms of partial derivatives.
Then, the equation becomes
DA
j
=
∂A
j
∂x
l
dx
l
+Γ
j
kl
A
k
dx
l
=
∂A
j
∂x
l
+Γ
j
kl
A
k
.
dx
l

17.4 Differentiation of Tensors 465
Since the left-hand side and dx
l
are contravariant vectors, we suspect that the
expression in parentheses is a tensor of type (1, 1). This can in fact be shown
directly. It is called the covariant derivative of A
j
with respect to x
l
and
denoted by A
j
;l
.Thus, covariant
derivative
A
j
;l
≡
∂A
j
∂x
l
+Γ
j
kl
A
k
. (17.55)
This is the generalization of ordinary derivative to situations in which the
affine connection is nonzero. Covariant derivative can similarly be defined
for covariant vectors as well as arbitrary tensors. For example, the covariant
derivative of T
ij
k
is a tensor of type (2, 2) given by
T
ij
k;q
=
∂T
ij
k
∂x
q
+Γ
i
pq
T
pj
k
+Γ
j
pq
T
ip
k
− Γ
p
kq
T
ij
p
.
Consider a curve in Euclidean space parametrized by t.LetA
i
(t)bethe parallel translation
along a curve
value of a vector field at a point on the curve. If dA
i
/dt = 0, then the vector is
constant along the curve, and we say that the vector is parallel translated
along the curve. When the affine connection is nonzero, we divide both
sides of the first equation in Box 17.4.1 by dt (which on the left we denote by
Dt for aesthetic reasons), and say that a contravariant vector field is parallel
translated along a curve if
DA
j
Dt
=0 or
dA
j
dt
+Γ
j
kl
A
k
dx
l
dt
=0, (17.56)
with a similar definition for a covariant vector field. Since A
j
depends on t only
through the coordinates, we use the chain rule dA
j
/dt =(∂A
j
/∂x
l
)dx
l
/dt to
rewrite the equation above as
DA
j
Dt
=
∂A
j
∂x
l
+Γ
i
kj
A
k
dx
l
dt
≡ A
j
;l
dx
l
dt
≡ A
j
;l
˙x
l
=0. (17.57)
A curve whose tangent vector is parallel translated along that curve is
geodesic and
geodesic equation
called a geodesic. The components of the vector tangent to a curve is
dx
i
/dt ≡ ˙x
i
. If we substitute this in (17.56) we obtain the following sec-
ond order differential equation called the geodesic equation:
D ˙x
j
Dt
=0, or
d
2
x
j
dt
2
+Γ
j
kl
dx
k
dt
dx
l
dt
=0, or ¨x
j
+Γ
j
kl
˙x
k
˙x
l
=0, (17.58)
where each super dot represents a differentiation with respect to t.Solving
this differential equation yields the parametric equation of a geodesic.
17.4.3 Metric Connection
The affine connection, which is defined by its transformation property of
(17.52) is completely arbitrary. One can define covariant differentials and

466 Tensor Anal ysi s
covariant derivatives in terms of any set of quantities that transform accord-
ing to Equation (17.52). With a metric tensor, however, one can define a
unique symmetric (therefore, torsion-free) affine connection called metric
connection given by
Γ
j
kl
=Γ
j
lk
=
1
2
g
jm
∂g
mk
∂x
l
+
∂g
ml
∂x
k
−
∂g
kl
∂x
m
≡ g
jm
Γ
mkl
, (17.59)
where
Γ
mkl
=
1
2
∂g
mk
∂x
l
+
∂g
ml
∂x
k
−
∂g
kl
∂x
m
, (17.60)
with all lower indices, is easier to remember. Note that it is the first index
of Γ
mkl
that is raised to give the components of the metric connection, and
for this reason the metric connection is sometimes denoted by Γ
j
kl
.The
verification that (17.59) is indeed an affine connection—i.e., that it transforms
according to (17.52)—is straightforward but tedious.
Example 17.4.1.
If all components of a metric tensor are constant in some coor-
dinate system, then all the components of the metric connection vanish. Note that
this is true only in that particular coordinate system. Changing coordinates changes
the affine connection, and in general, the components of a metric connection will
not be zero even if they are zero in some coordinate system. If we use Cartesian
coordinates, then the Euclidean metric is just the Kronecker delta. Therefore, all
components of the metric connection are zero. Similarly, the metric of special rel-
ativity in Cartesian coordinates in η
αβ
, whose components are either 0 or 1 or −1.
Hence, all components of the metric connection of special relativity in Cartesian
coordinates vanish.
The metric connection has some special properties which are of physical
importance. The first property which could be easily verified is that
g
ij;k
=0 or
∂g
ij
∂x
k
− Γ
p
jk
g
ip
− Γ
p
ik
g
pj
=0. (17.61)
The second property is that between any two points passes a single geodesic
of the metric connection, and this geodesic extremizes the distance between
the two points. If the geometry is Riemannian (i.e., if the metric is positive
definite) then the geodesic gives the shortest distance. In relativity, where the
metric is not Riemannian, the geodesics give the longest distance.
Example 17.4.2.
In this example, we find the geodesics of a sphere. The spherical
angular coordinates θ and ϕ can be used on the surface of a sphere of radius a.From
the element of length ds
2
= a
2
dθ
2
+ a
2
sin
2
θdϕ
2
on this sphere, and using θ and ϕ
to label components, we deduce that
g
11
≡ g
θθ
= a
2
,g
22
≡ g
ϕϕ
= a
2
sin
2
θ, g
12
≡ g
θϕ
= g
21
≡ g
ϕθ
=0,
and similarly,
g
11
≡ g
θθ
=
1
a
2
,g
22
≡ g
ϕϕ
=
1
a
2
sin
2
θ
,g
12
≡ g
θϕ
= g
21
≡ g
ϕθ
=0.
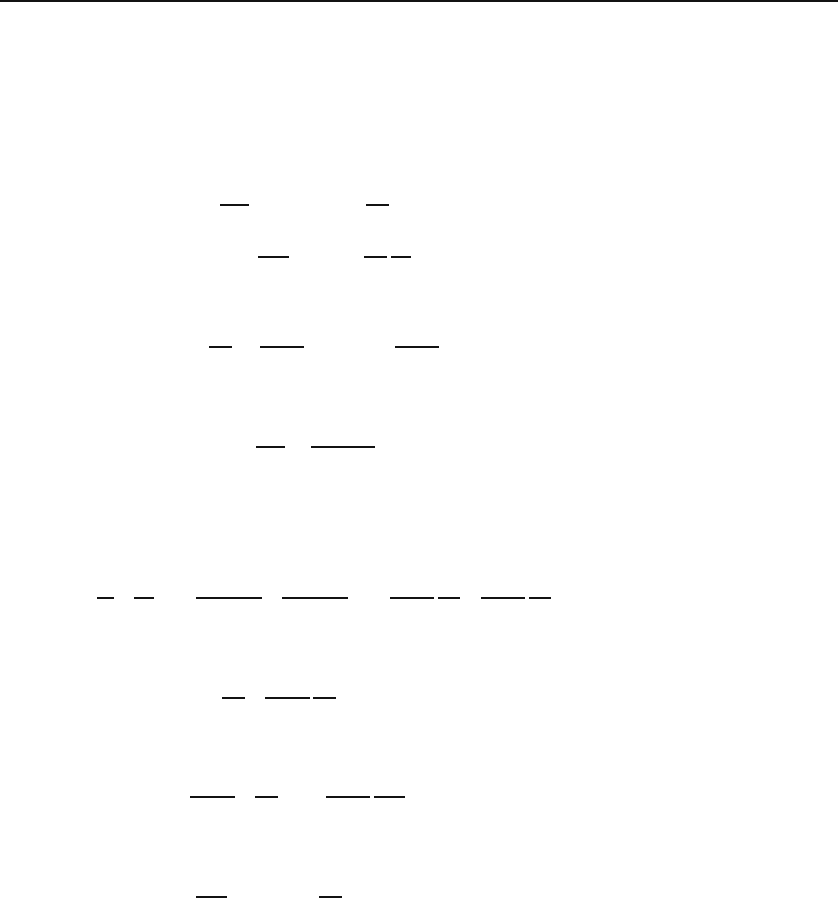
17.4 Differentiation of Tensors 467
Substituting these in (17.59), we can calculate the components of the affine connec-
tion. The nonzero components turn out to be
Γ
θ
ϕϕ
= −sin θ cos θ, Γ
ϕ
θϕ
=Γ
ϕ
ϕθ
=cotθ.
Using these in the geodesic equation (17.58), we obtain the following two differential
equations:
d
2
θ
dt
2
− sin θ cos θ
dϕ
dt
2
=0,
d
2
ϕ
dt
2
+2cotθ
dϕ
dt
dθ
dt
=0. (17.62)
The second equation can be solved to give
dϕ
dt
=
C
sin
2
θ
⇒ dϕ =
C
sin
2
θ
dt, (17.63)
where C is a constant of integration. Substituting this in the first equation of (17.62)
gives
d
2
θ
dt
2
−
C
2
cos θ
sin
3
θ
=0. (17.64)
To find the geodesic, it is more convenient to express θ as a function of ϕ.This
means changing the independent variable in Equation (17.64) from t to ϕ.Thisis
done formally by using the second equation of (17.63) to substitute for dt in (17.62).
Thus, the first tem of (17.62) can be written as
d
dt
dθ
dt
=
Cd
sin
2
θdϕ
Cdθ
sin
2
θdϕ
=
C
2
sin
2
θ
d
dϕ
1
sin
2
θ
dθ
dϕ
.
Substituting this in (17.64) yields
d
dϕ
1
sin
2
θ
dθ
dϕ
− cot θ =0.
Differentiating the first term, we get
−2
cos θ
sin
3
θ
dθ
dϕ
2
+
1
sin
2
θ
d
2
θ
dϕ
2
− cot θ =0,
which can be simplified to the following differential equation:
sin θ
d
2
θ
dϕ
2
− 2cosθ
dθ
dϕ
2
− sin
2
θ cos θ =0. (17.65)
If we could solve this equation, we would find θ as a function of ϕ,andthis
should be the equation of a geodesic on a sphere. Instead, let us use our knowledge
of the geodesics (curves giving the shortest distance) on a sphere, write it with θ as
a function of ϕ and see if it satisfies (17.65). Our sphere is parametrized as
x = a sin θ cos ϕ, y = a sin θ sin ϕ, z = a cos θ.
The great circles—curves of shortest distance—are the intersection of a plane passing
through the origin and the sphere. Such a plane has an equation of the form Ax +

468 Tensor Anal ysi s
By + Cz = 0. The intersection with the sphere is obtained by substituting for x, y,
and z from the above equations:
Aa sin θ cos ϕ + Ba sin θ sin ϕ + Ca cos θ =0.
Dividing by Casin θ and redefining A to be −A/C and B to be −B/C,weget
cot θ = A cos ϕ + B sin ϕ,
as the equation of geodesic on a sphere. It is straightforward to show that this
equation indeed satisfies (17.65).
17.5 Riemann Curvature Tensor
Consider a closed loop, such as a rectangle, on a flat surface. Start a vector
at one point of the rectangle (the lower left corner) and carry it parallel to
itself to the point diagonally opposite the initial point [Figure 17.1(a)]. In one
case carry the vector to the right and then up. In the second case carry the
vector up and then to the right. Compare the vector at the end of the two
cases. They are equal. Do the same on a curved space such as the surface of a
sphere. The two vectors at the end do not coincide [see Figure 17.1(b)]! The
degree to which they are different is a measure of the curvature of the space.
Let us quantify the notion of the curvature. Suppose that the lower and
upper curves of the “rectangle” are parametrized by t and the right and the
left curves by s.Movingalongacurveparametrizedbyt does not change s,
and vice versa. Using a Taylor expansion, in which derivatives are replaced
by covariant derivatives, parallel translate a contravariant vector A
j
first to
the right and then upward [see Figure 17.1(b) for clarification]. Assume that
the lower left corner has (t, s) as the parameter values. As you move along
the lower curve, the parameters change from (t, s)to(t +Δt, s). So, to first
order in Δt,wehave
A
j
(t +Δt, s)=A
j
(t, s)+
DA
j
Dt
Δt = A
j
(t, s)+A
j
;l
(t, s)
dx
l
dt
Δt.
(a)
(b)
Figure 17.1: (a) In a flat space, the direction of the vector does not change when
carried along two different paths. (b) In a curved space, the two vectors are different.
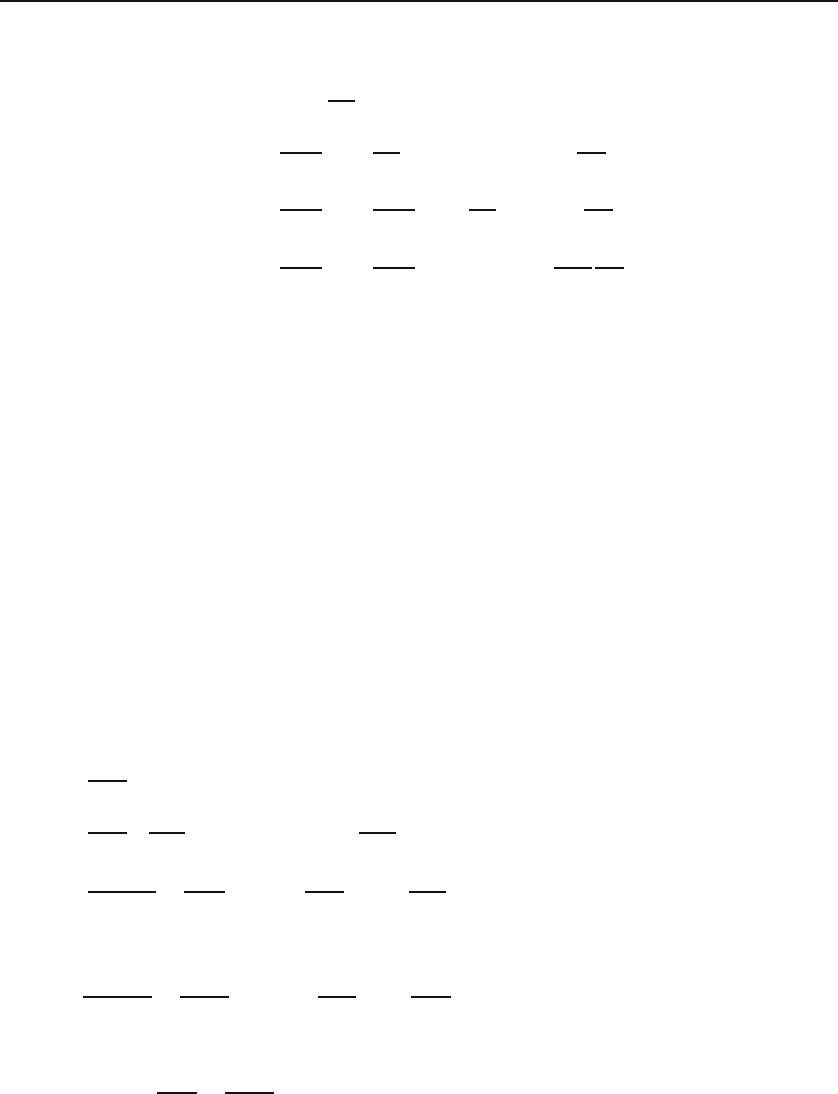
17.5 Riemann Curvature Tensor 469
Now parallel translate this vector upward, the direction in which t is constant
but s changes:
A
j
(t +Δt, s +Δs)=A
j
(t +Δt, s)+
D
Ds
(A
j
(t +Δt, s))Δs
= A
j
(t, s)+
DA
j
Dt
Δt +
D
Ds
A
j
(t, s)+A
j
;l
(t, s)
dx
l
dt
Δt
Δs
= A
j
(t, s)+
DA
j
Dt
Δt +
DA
j
Ds
Δs +
D
Ds
A
j
;l
(t, s)
dx
l
dt
Δt
Δs
= A
j
(t, s)+
DA
j
Dt
Δt +
DA
j
Ds
Δs + A
j
;l;m
(t, s)
dx
m
ds
dx
l
dt
ΔtΔs.
Since A
j
is assumed to be parallel translated on both curves, DA
j
/Dt =0=
DA
j
/Ds,and
A
j
(t +Δt, s +Δs)
1
= A
j
(t, s)+A
j
;l;m
(t, s)Δx
l
Δx
m
,
whereweusedΔx
l
≈ (dx
l
/dt)Δt and Δx
m
≈ (dx
m
/ds)Δs. The subscript 1
on the left hand side stands for the “first route.” The “second route” is going
up first and then to the right. It should be clear that the only difference in
the final result is the interchange of l and m. We therefore have
A
j
(t +Δt, s +Δs)
2
= A
j
(t, s)+A
j
;m;l
(t, s)Δx
l
Δx
m
.
Thus, using A
j
;lm
for the second covariant derivative, we have
A
j
(t+Δt, s+Δs)
1
−A
j
(t+Δt, s+Δs)
2
=
A
j
;lm
− A
j
;ml
Δx
l
Δx
m
. (17.66)
The difference in parentheses should be related to the curvature of the space
(manifold) under consideration.
Finding this difference is straightforward. Using the rule of covariant dif-
ferentiation for general tensors, we get
A
j
;lm
=
∂A
j
;l
∂x
m
+Γ
j
km
A
k
;l
− Γ
p
lm
A
j
;p
=
∂
∂x
m
∂A
j
∂x
l
+Γ
j
kl
A
k
+Γ
j
km
∂A
k
∂x
l
+Γ
k
rl
A
r
− Γ
p
lm
A
j
;p
=
∂
2
A
j
∂x
m
∂x
l
+
∂Γ
j
kl
∂x
m
A
k
+Γ
j
kl
∂A
k
∂x
m
+Γ
j
km
∂A
k
∂x
l
+Γ
j
km
Γ
k
rl
A
r
− Γ
p
lm
A
j
;p
.
Inthelastlineswitchl and m to get A
j
;ml
:
A
j
;ml
=
∂
2
A
j
∂x
l
∂x
m
+
∂Γ
j
km
∂x
l
A
k
+Γ
j
km
∂A
k
∂x
l
+Γ
j
kl
∂A
k
∂x
m
+Γ
j
kl
Γ
k
rm
A
r
− Γ
p
ml
A
j
;p
.
Subtracting, and changing the dummy indices when necessary, we obtain
A
j
;lm
− A
j
;ml
=
∂Γ
j
kl
∂x
m
−
∂Γ
j
km
∂x
l
+Γ
j
rm
Γ
r
kl
− Γ
j
rl
Γ
r
km
A
k
− (Γ
p
lm
− Γ
p
ml
) A
j
;p
.
(17.67)

470 Tensor Anal ysi s
It is straightforward but tedious to show that the expression in the first
pair of parentheses transforms as a component of a tensor of type (1, 3). This
tensor is denoted by R
j
klm
and is called Riemann curvature tensor:Riemann
curvature tensor
R
j
klm
=
∂Γ
j
kl
∂x
m
−
∂Γ
j
km
∂x
l
+Γ
j
rm
Γ
r
kl
− Γ
j
rl
Γ
r
km
. (17.68)
The expression in the second pair of parentheses in (17.67) is the torsion tensor
introduced earlier [see Equation (17.53) and the discussion after it].
Example 17.5.1.
Example 17.4.1 showed that the metric connection of Euclidean
space and special relativistic spacetime in Cartesian coordinates are both zero.
Equation (17.68) shows that for these spaces, the Riemannian curvature tensor
expressed in Cartesian coordinates is zero. Since Riemannian curvature tensor is aflat spaces (or
manifolds) tensor,itmustbezeroin all coordinates, as expressed in Box 17.2.2. Spaces that
have zero Riemannian curvature tensor are called flat. We thus see that flatness
is an intrinsic property of a space, independent of any coordinates used in that
space.
The curvature tensor has some important properties which we state with-
out proof. One property that is evident from (17.68) is
.R
j
klm
= −R
j
kml
(17.69)
The second property, which is true only if the torsion tensor vanishes, i.e.,
when the affine connection is symmetric, is
R
j
klm
+ R
j
lmk
+ R
j
mkl
=0. (17.70)
The third property, which involves the covariant derivative of the curvature
Bianchi identity
tensor and is true only for torsion-free connections, is
R
j
klm;i
+ R
j
kmi;l
+ R
j
kil;m
=0. (17.71)
This is also called the Bianchi identity. The last property, which holds for
Riemannian tensor of the metric connection, is that R
j
klm
has n
2
(n
2
− 1)/12
components.
Various other tensors can be obtained from the Riemann curvature tensor
by contraction. For example, by contracting the contravariant index with the
last covariant index one obtains the so-called Ricci tensor:
Ricci tensor and
scalar curvature
R
kl
= R
j
klj
= R
j
klj
=
∂Γ
j
kl
∂x
j
−
∂Γ
j
kj
∂x
l
+Γ
j
rj
Γ
r
kl
− Γ
j
rl
Γ
r
kj
, (17.72)
and by raising one of the Ricci tensor’s indices and contracting, we obtain the
scalar curvature:
R = R
l
l
= g
kl
R
kl
. (17.73)
Einstein’s general theory of relativity explains gravity as a manifestation
of the curvature of spacetime. Since gravity is caused by mass, and since
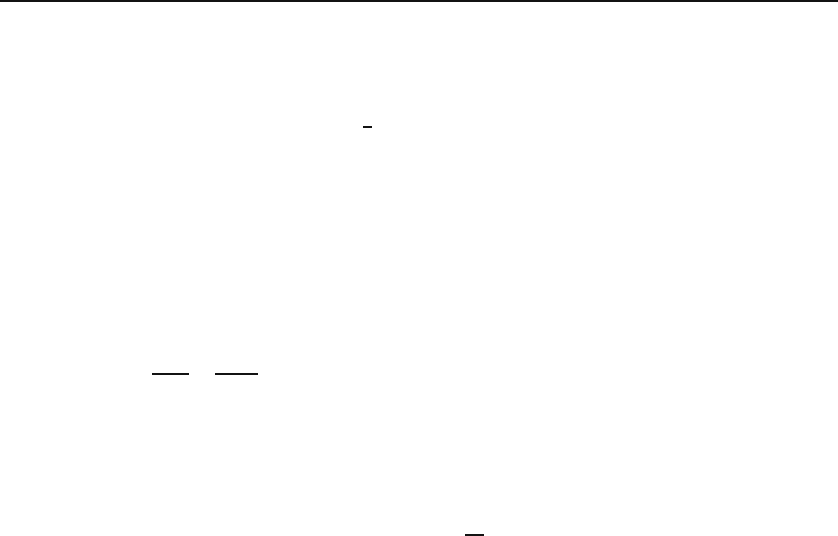
17.6 Problems 471
mass and energy are equivalent, the source of curvature is energy. Pursuing Einstein curvature
tensor and
Einstein equation
this idea, Einstein came up with an equation, the Einstein equation,that
describes all (large scale) gravitational interactions. Defining the Einstein
curvature tensor as
G
ij
≡ R
ij
−
1
2
g
ij
R, (17.74)
the Einstein equation is written as
G
ij
=8πGT
ij
, (17.75)
where G is the universal gravitational constant and T
ij
is the energy momen-
tum tensor.
Example 17.5.2.
For the sphere of Example 17.4.2, the Ricci curvature tensor
canbewrittenas
R
kl
=
∂Γ
θ
kl
∂θ
−
∂Γ
ϕ
kϕ
∂x
l
+Γ
ϕ
θϕ
Γ
θ
kl
− Γ
θ
ϕl
Γ
ϕ
kθ
− Γ
ϕ
θl
Γ
θ
kϕ
− Γ
ϕ
ϕl
Γ
ϕ
kϕ
Using this, it is easy to show that R
θϕ
=0=R
ϕθ
, while
R
θθ
=1,R
ϕϕ
=sin
2
θ
Furthermore, since g
θθ
=1/a
2
and g
ϕϕ
=1/(a
2
sin
2
θ), the scalar curvature becomes
R = g
ij
R
ij
= g
θθ
R
θθ
+ g
ϕϕ
R
ϕϕ
=
2
a
2
showing that a sphere is a space of constant (and positive) curvature, as we
expect.
17.6 Problems
17.1. Write ∂
i
x
j
in a form that includes the Kronecker delta. Now show that
∇ · r =3.
17.2. Recall that a homogeneous function f of n variable of degree q satisfies
qf(x
1
,x
2
,...,x
n
)=
n
i=1
x
i
∂
i
f.
(a) Differentiate both sides with respect to x
j
and show that
(q − 1)∂
j
f(x
1
,x
2
,...,x
n
)=
n
i=1
x
i
∂
i
∂
j
f.
(b) Multiply this equation by x
j
and sum over j to obtain
q(q − 1)f(x
1
,x
2
,...,x
n
)=
n
i,j=1
x
i
x
j
∂
i
∂
j
f.
