Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


442 Tensor Anal ysi s
In terms of a free index, we can rewrite this as
¯x
i
= a
i1
x
1
+ a
i2
x
2
+ a
i3
x
3
,i=1, 2, 3,
and using the summation notation
¯x
i
=
3
j=1
a
ij
x
j
,i=1, 2, 3.
Finally, using the Einstein summation convention and always keeping in mind
that the free index i takes the values 1, 2, or 3, we come up with the following
very succinct replacement for 17.3
¯x
i
= a
ij
x
j
. (17.4)
Equations (17.3) and (17.4) are identical despite the enormous brevity of the
latter.
As an application of the use of indices and summation convention, we
conveniently express the rule of matrix multiplication, which we shall use
frequently. Box 6.1.3 gives this rule. Let C = AB be the product of A and B.
Then the rule in Box 6.1.3 can be written as
c
ij
= a
ik
b
kj
. (17.5)
Notice that here we have two free indices i and j. The index k is being
summedoverontheright.
Of particular importance are transformations that leave the dot product
intact. We called these transformations orthogonal (see Section 6.1.3). These
orthogonal transformations satisfy Equation (6.20), which could be written in
terms of indices. Noting that the ij-th element of the unit matrix is δ
ij
,the
familiar Kronecker delta, which as the reader may recall, is defined as
δ
ij
≡
0
1ifi = j,
0ifi = j,
(17.6)
we rewrite (6.20) as
8
A
ik
(A)
kj
=(1)
ij
or a
ki
a
kj
= δ
ij
. (17.7)
Now multiply both sides of (17.4) by a
ik
and sum over i to getKronecker delta in
asum
a
ik
¯x
i
= a
ik
a
ij
=δ
kj
x
j
= x
k
,
where in the last step we used the most important property of the Kronecker
delta:
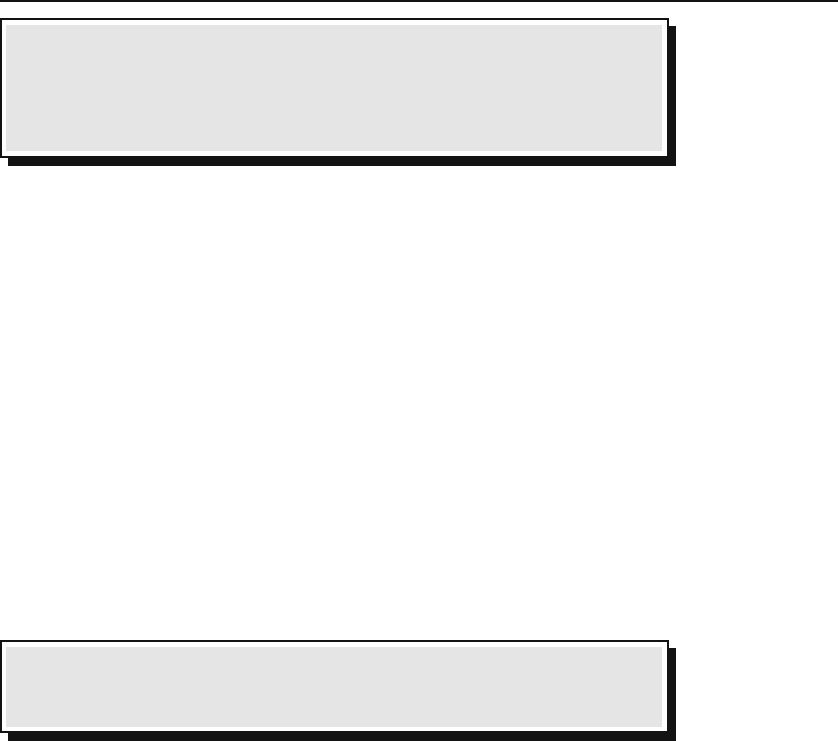
17.1 Vectors and Indices 443
Box 17.1.3. When an indexed quantity shares a common repeated index
with the Kronecker delta (thus a sum over that index understood), the
result is an expression in which both the sum and the Kronecker delta are
removed and the repeated index of the indexed quantity is replaced by the
other index of the Kronecker delta.
Thus the inverse of Equation (17.4) is
x
j
= a
ij
¯x
i
. (17.8)
Note the difference in the position of the dummy index between this equation
and (17.4).
Equations (17.4) and (17.8) give the transformation rules for the compo-
nents of the position vector when one goes from one Cartesian coordinate
system to another. It should be clear that the same transformation rules
apply to the components of any vector, as long as one adheres to Cartesian
coordinate systems. Thus if V
i
and
¯
V
i
represent the components of a vector
V in two Cartesian coordinate systems, then
¯
V
i
= a
ij
V
j
and V
j
= a
ij
¯
V
i
. (17.9)
In fact, it is customary to define vectors in terms of their transformation
properties:
vectors defined in
terms of their
transformation
property
Box 17.1.4. A set of quantities V
i
is said to be the components of a
Cartesian vector V if, under the orthogonal transformation (17.4), the
transformed quantities
¯
V
i
and the original quantities are related by (17.9).
Section 1.3 introduced the idea of expressing vectors in different coordinate
systems, mainly Cartesian, cylindrical, and spherical. In all cases, care was
taken to use orthogonal unit vectors. In fact, this has been the sole practice
throughout the book so far, and for good reason: the dot product of two
vectors—and hence length of a vector, defined as the square root of the dot
product of the vector with itself—does not change when their components in
one set of orthogonal unit vectors are written in terms of their components in
another set of orthogonal unit vectors. This actually defines the orthogonal
transformation of Section 6.1.3, and Equation (6.20) or (17.7) guarantees the
invariance of the length of a vector.
Orthogonal transformations are not always the most suitable. As an exam-
ple, consider a curve in space parametrized in a Cartesian coordinate system
by x
i
= f
i
(t), where f
1
(t), f
2
(t), and f
3
(t) are some smooth functions. The
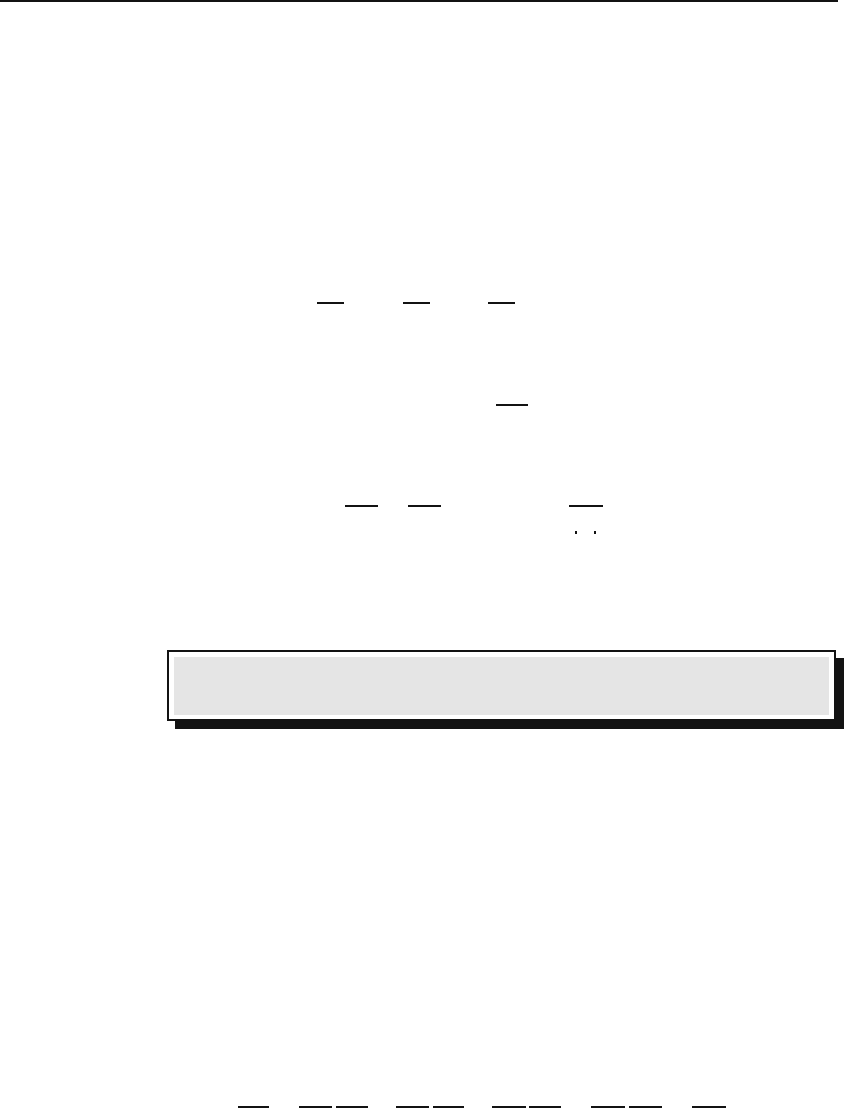
444 Tensor Anal ysi s
tangent to this curve—a vector—has components ˙x
i
≡ dx
i
/dt = f
i
(t). Now
consider a new coordinate system, not necessarily Cartesian, given by
¯x
i
= g
i
(x
1
,x
2
,x
3
). (17.10)
The curve can be written in terms of the new coordinates by substituting f
i
(t)
for each x
i
:
¯x
i
= g
i
(f
1
(t),f
2
(t),f
2
(t)) ≡ h
i
(t),
where the last identity defines the function h
i
(t). The components of the
tangent to the curve in the new coordinate system are given by the chain
rule:
˙
¯x
i
= h
i
(t)=∂
1
g
i
df
1
dt
+∂
2
g
i
df
2
dt
+∂
3
g
i
df
3
dt
= ∂
1
g
i
˙x
1
+∂
2
g
i
˙x
2
+∂
3
g
i
˙x
3
= ∂
j
g
i
˙x
j
.
Recalling that ∂
j
g
i
= ∂g
i
/∂x
j
and that g
i
=¯x
i
, this is usually written as
˙
¯x
i
=
∂¯x
i
∂x
j
˙x
j
. (17.11)
It is instructive to see what happens if ¯x
i
is given by (17.4). In that case,
we have
∂¯x
i
∂x
j
=
∂
∂x
j
a
ik
x
k
!
= a
ik
∂x
k
∂x
j
=δ
kj
= a
ij
, (17.12)
where we have used an obvious property of partial derivative which is so useful
that it is worth boxing it:
Box 17.1.5. If {y
1
,y
2
,...,y
m
} are independent variables, then ∂y
i
/∂y
j
=
δ
ij
.
Equation (17.12) shows that, when applied to Cartesian coordinate transfor-
mations, (17.11) is consistent with the definition of a vector as given in Box
17.1.4.
What about the inverse of (17.11)? Equation (17.10) can be treated as
three equations in the three unknowns {x
1
,x
2
,x
3
}. One can then solve these
unknowns as functions of the independent variables
,
¯x
1
, ¯x
2
, ¯x
3
-
.Whether
or not one can actually solve (17.10) for
,
¯x
i
-
depends on the form of the
functions {g
1
,g
2
,g
3
}. If these functions satisfy certain (mild) mathematical
properties, then Equation (17.10) is said to be invertible and each x
j
can
be written as a function of the independent variables
,
¯x
i
-
. We assume that
(17.10) is indeed invertible.
Treating x
j
as dependent and
,
¯x
i
-
as independent variables, using the
chain rule, and employing obvious notation, we can write
˙x
j
=
dx
j
dt
=
∂x
j
∂¯x
1
d¯x
1
dt
+
∂x
j
∂¯x
2
d¯x
2
dt
+
∂x
j
∂¯x
3
d¯x
3
dt
=
∂x
j
∂¯x
k
d¯x
k
dt
=
∂x
j
∂¯x
k
˙
¯x
k
. (17.13)

17.1 Vectors and Indices 445
Is this consistent with Equation (17.11)? In other words, if we substitute ˙x
j
from this equation into the right-hand side of (17.11), do we get
˙
¯x
i
?Let’s
try it!
RHS of (17.11) =
∂¯x
i
∂x
j
˙x
j
=
∂¯x
i
∂x
j
∂x
j
∂¯x
k
˙
¯x
k
=
∂¯x
i
∂¯x
k
˙
¯x
k
= δ
ik
˙
¯x
k
=
˙
¯x
i
,
where in the third equality we used the chain rule (2.16), in the fourth equality
we used Box 17.1.5 as applied to the independent variables ¯x
i
,andinthelast
equality we used Box 17.1.3. Thus, Equation (17.13) is indeed consistent with
(17.11). It is tempting to call objects which transform according to (17.11)
components of a vector. But before jumping to conclusions, let’s look at
another vector with which we are familiar.
17.1.2 Covariant and Contravariant Vectors
The gradient of a function was first defined in Section 12.3. It is a vector
whose components are essentially derivatives of the function with respect to
the coordinates. Because we are interested in the transformation properties of
objects, we first have to clarify the notion of a function.Ascalar function is
a physical quantity, such as temperature, which takes on a single value at each
point of space. Now, a point has an existence independent of any coordinate
scalar function
systems. Nevertheless, coordinates are useful for calculations. And if the point
is described by (x
1
,x
2
,x
3
) in a coordinate system, and φ denotes the scalar
function, then we write φ(x
1
,x
2
,x
3
) for the value of the scalar function at
that point. The same point is described by (¯x
1
, ¯x
2
, ¯x
3
) in another coordinate
system, and the value of the scalar function in terms of the new coordinates is
¯
φ(¯x
1
, ¯x
2
, ¯x
3
). It should be obvious that the form of the scalar function changes
when one changes the coordinates. Thus the notation
¯
φ instead of φ. Clearly,
¯
φ(¯x
1
, ¯x
2
, ¯x
3
)=φ(x
1
,x
2
,x
3
). (17.14)
Now differentiate both sides with respect to ¯x
i
. The left side gives the ith
component of the gradient of
¯
φ; and using the chain rule on the right side, we
get
∂φ
∂¯x
i
=
∂φ
∂x
1
∂x
1
∂¯x
i
+
∂φ
∂x
2
∂x
2
∂¯x
i
+
∂φ
∂x
3
∂x
3
∂¯x
i
=
∂φ
∂x
j
∂x
j
∂¯x
i
.
We thus obtain
∂
¯
φ
∂¯x
i
=
∂x
j
∂¯x
i
∂φ
∂x
j
, (17.15)
which is a different transformation than (17.11).
It appears that we have two kinds of vectors: those whose components
transform according to (17.11) and those transforming according to (17.15).
To further elucidate the discussion, let’s look at the dot product. Let A and
B be vectors which transform according to (17.11):
¯
A
i
=
∂¯x
i
∂x
j
A
j
,
¯
B
i
=
∂¯x
i
∂x
k
B
k
.
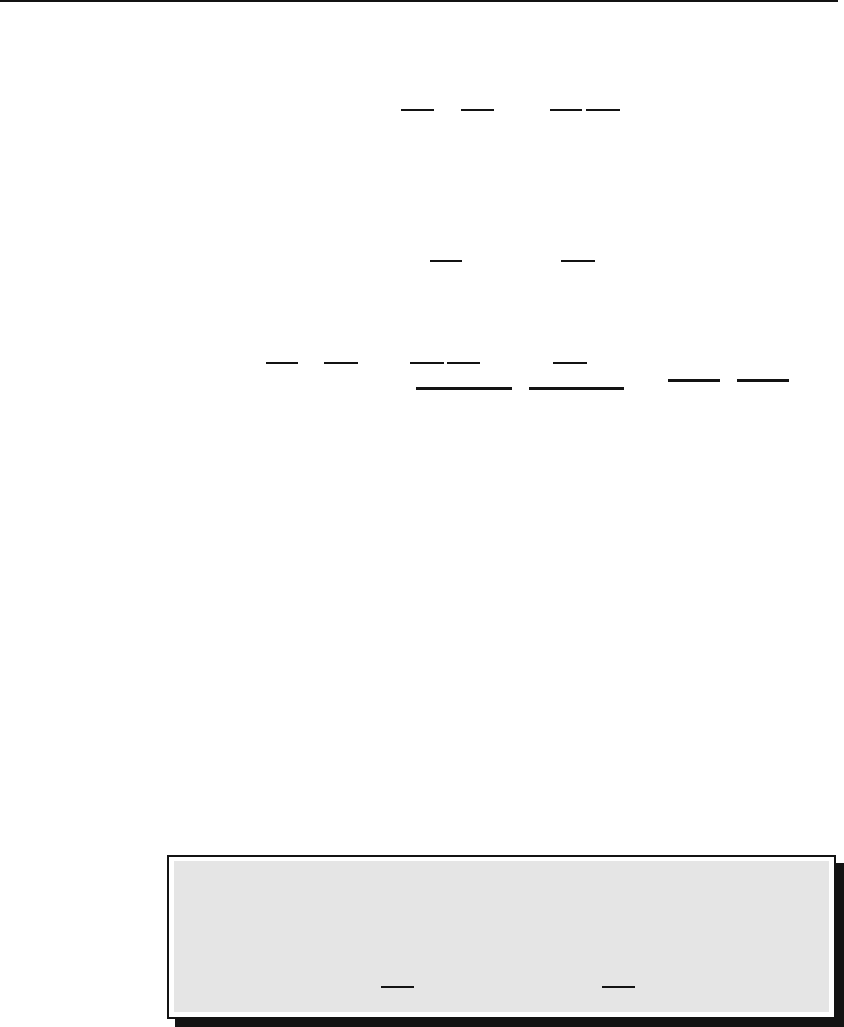
446 Tensor Anal ysi s
The dot product in the ¯x coordinate system is
¯
A
i
¯
B
i
(sum over repeated indices
understood!). Write this in terms of the x coordinates:
¯
A
i
¯
B
i
=
∂¯x
i
∂x
j
A
j
∂¯x
i
∂x
k
B
k
=
∂¯x
i
∂x
j
∂¯x
i
∂x
k
A
j
B
k
.
The right-hand side does not reduce to a dot product.
Now consider one vector U that transforms according to (17.11) and an-
other V that transforms according to (17.15)
¯
U
i
=
∂¯x
i
∂x
j
U
j
,
¯
V
i
=
∂x
k
∂¯x
i
V
k
,
and take the dot product of these two vectors:
¯
U
i
¯
V
i
=
∂¯x
i
∂x
j
U
j
∂x
k
∂¯x
i
V
k
=
∂x
k
∂¯x
i
∂¯x
i
∂x
j
U
j
V
k
=
∂x
k
∂x
j
U
j
V
k
by the chain rule
= δ
kj
U
j
V
k
= U
j
V
j
by Box 17.1.3
.
(17.16)
This is the magic of a general coordinate transformation! Although the func-
tions {g
1
,g
2
,g
3
} of (17.10) are completely arbitrary (except for invertibility),
they respect the dot product, as long as one vector transforms according to
(17.11) and the other according to (17.15).
So far we have been considering coordinates in a three-dimensional space.
However, as this section’s discussion easily points out, nothing prevents us
from generalizing to n-dimensions: the only change we have to make is that
the sums (and the repeated indices that imply them) should go from 1 to n.
For example, (17.10) becomes
¯x
i
= g
i
(x
1
,x
2
,...,x
n
),i=1, 2,...,n. (17.17)
And this generalization is not purely academic, because, as we saw in Chapter
covariant and
contravariant
vectors
8, relativity demands a four -dimensional spacetime. Having this generaliza-
tion in mind, we make the following definition of the two kinds of vector
discussed above:
Box 17.1.6. The quantities {A
1
,A
2
,...A
n
} and {B
1
,B
2
,...B
n
} are said
to constitute the components of a contravariant and a covariant vector,
respectively, if, under a coordinate transformation (17.17) they transform
according to
¯
A
i
=
∂¯x
i
∂x
j
A
j
and
¯
B
i
=
∂x
j
∂¯x
i
B
j
. (17.18)
Note the placement of the indices on the two types of vector. Only when
an “upper” index appears with a “lower” index in a sum is the result (the dot

17.2 From Vectors to Tensors 447
product) independent of the coordinate system used. Now the question arises:
If one needs an upper and a lower index in the sum to get a quantity that is
invariant, how does one define the length of a contravariant vector (which has
only an upper index) or a covariant vector (which has only a lower index)?
For this, we need to wait until we have introduced tensors and, in particular,
the metric tensor.
17.2 From Vectors to Tensors
We have already discussed one kind of multiplication of vectors, the dot prod-
uct [see Equation (17.2)]. Now we consider the cross product as a prototype
of objects that have more than one index. The cross product of two vec-
tors involves different components of those vectors (as opposed to the same
components involved in the inner product). In terms of the index labels intro-
duced above, this means that the cross product carries two indices. In fact,
consider two (covariant) vectors A
i
and B
j
. The components of their cross
product are of the form A
i
B
j
− A
j
B
i
. In another coordinate system related
to the first by (17.10), the components are
¯
A
i
¯
B
j
−
¯
A
j
¯
B
i
. Using (17.18) in
Box 17.1.6 for A and B,weget
¯
A
i
¯
B
j
=
∂x
k
∂¯x
i
A
k
∂x
h
∂¯x
j
B
h
=
∂x
k
∂¯x
i
∂x
h
∂¯x
j
A
k
B
h
,
and
¯
A
j
¯
B
i
=
∂x
k
∂¯x
j
A
k
∂x
h
∂¯x
i
B
h
=
∂x
k
∂¯x
j
∂x
h
∂¯x
i
A
k
B
h
=
∂x
h
∂¯x
j
∂x
k
∂¯x
i
A
h
B
k
,
where in the last step we just changed the dummy indices [see Equation (9.4)].
Subtracting the last two equations, we get
¯
A
i
¯
B
j
−
¯
A
j
¯
B
i
=
∂x
k
∂¯x
i
∂x
h
∂¯x
j
(A
k
B
h
− A
h
B
k
).
Thus, if we define C
kh
≡ A
k
B
h
−A
h
B
k
as the components of A ×B,thelast cross product as a
two-indexed
quantity
equation gives their transformation property:
¯
C
ij
=
∂x
k
∂¯x
i
∂x
h
∂¯x
j
C
kh
. (17.19)
Cross products are special cases of a more general category of mathemat-
ical objects called tensors which carry multiple indices. Some of the indices
may be upper, some lower. The most general tensor carries multiple upper
and multiple lower indices.

448 Tensor Anal ysi s
Box 17.2.1. Asetofn
r+s
quantities T
i
1
...i
r
j
1
...j
s
is said to constitute the com-
ponents of a tensor T of type (r, s) if, under a coordinate transformation
(17.17) they transform according to
T
i
1
...i
r
j
1
...j
s
=
∂¯x
i
1
∂x
h
1
···
∂¯x
i
r
∂x
h
r
∂x
k
1
∂¯x
j
1
···
∂x
k
s
∂¯x
j
s
T
h
1
...h
r
k
1
...k
s
(17.20)
{i
1
...i
r
} and {j
1
...j
s
} are called the contravariant and covariant
indices, respectively. The rank of the tensor is defined as r + s.
Note that for every index on the left there is an identical index on the right,
and that only an upper index and its lower partner are repeated on the right.
Here we are using the obvious convention that in the partial derivatives of the
form ∂x
k
/∂¯x
j
or ∂¯x
k
/∂x
j
, k is considered an upper index and j a lower one.
Example 17.2.1.
When we introduced multipoles in Chapter 10, we were able to
write the potential of a source distribution as an infinite sum of moments of source of
higher and higher order. Although Cartesian coordinates are extremely clumsy for
higher moments, the third moment can be handled neatly in Cartesian coordinates
once we use the machinery of indices developed in this section.
Recall that the integrand of the third term in the expansion of potential is [see
Equation (10.33)]
Integrand ≡ r
2
−
1
2
+
3
2
(
ˆ
e
r
·
ˆ
e
r
)
2
= −
r
2
2
+
3
2
r
2
r · r
rr
2
.
Writing the position vectors in terms of their Cartesian components and rearranging
terms yields
Integrand =
3
2
(xx
+ yy
+ zz
)
2
r
2
−
r
2
2
=
1
2r
2
,
x
2
(3x
2
− r
2
)+y
2
(3y
2
− r
2
)+z
2
(3z
2
− r
2
)
+6xyx
y
+6xzx
z
+6yzy
z
-
. (17.21)
We want to express (17.21) in terms of indices. First let us concentrate on the terms
involving x
2
, y
2
,andz
2
.Sincethesediagonal terms involve x
2
= x
1
x
1
, etc., it is
natural to define a two-indexed quantity, say V
ij
, such that
x
2
(3x
2
− r
2
) ≡ x
1
x
1
V
11
,
y
2
(3y
2
− r
2
) ≡ x
2
x
2
V
22
,
z
2
(3z
2
− r
2
) ≡ x
3
x
3
V
33
,
with
V
11
=3x
1
x
1
− r
2
,V
22
=3x
2
x
2
− r
2
,V
33
=3x
3
x
3
− r
2
.
Next, we note that the off-diagonal terms such as 6xyx
y
can be written as 6x
i
x
j
x
i
x
j
(no summation!). It appears as if we can write all terms in the last line of Equation
(17.21) as
3
i,j=1
x
i
x
j
V
ij
if we can define V
ij
properly. The off-diagonal sum sug-
gests defining V
ij
as V
ij
≡ 3x
i
x
j
. The reader may wonder why we did not include
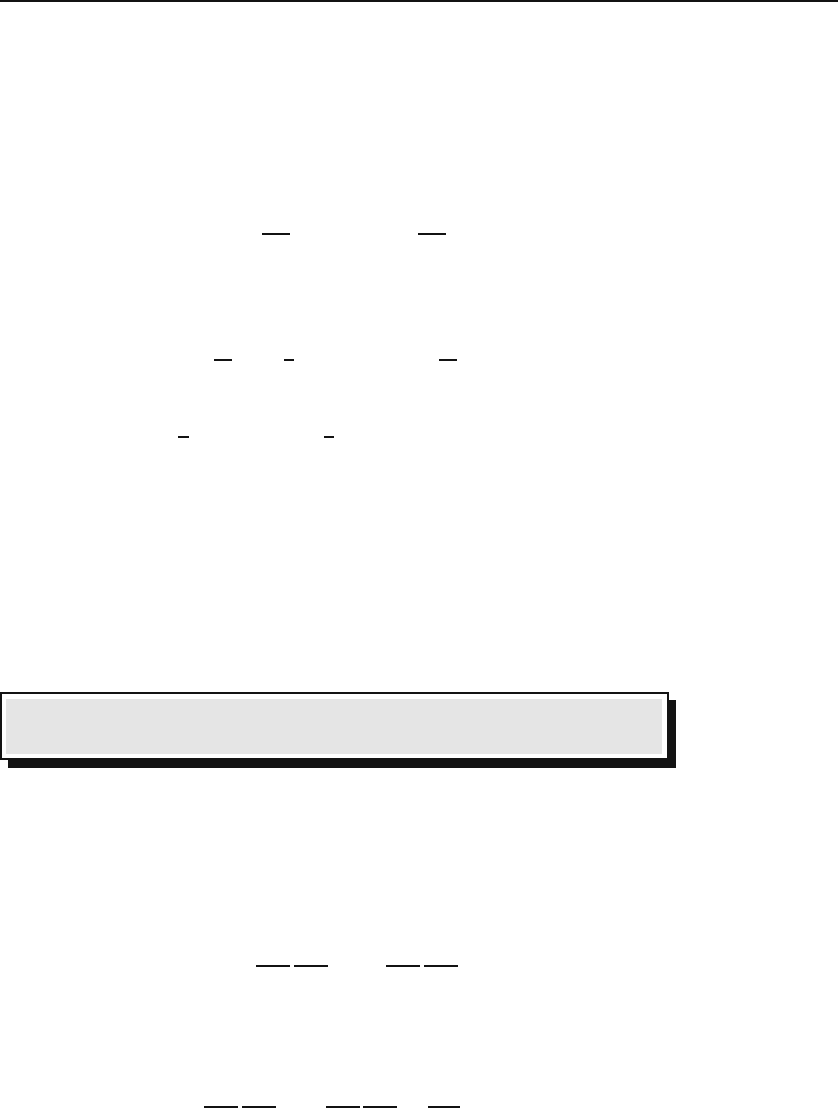
17.2 From Vectors to Tensors 449
the factor of 6 in the definition. The reason is that when summed over indices, the
symmetry of V
ij
under interchange of its indices automatically introduces a factor
of 2. The problem with this definition is that when i = j, i.e., when evaluating the
diagonal terms, the r
2
term is absent. To remedy this, we change the definition to
V
ij
≡ 3x
i
x
j
− r
2
δ
ij
. (17.22)
Then, the Kronecker delta contributes only to the diagonal terms as it should. The
reader is urged to show that
Integrand =
1
2r
2
3
i,j=1
x
i
x
j
V
ij
=
1
2r
2
x
i
x
j
V
ij
, (17.23)
where in the last equality the summation convention is implied.
Now we substitute this in Equation (10.33) and denote the third term as Φ
3
(r).
This yields
Φ
3
(r)=
K
r
5
x
i
x
j
1
2
#
Ω
V
ij
dQ(r
)
≡
K
r
5
x
i
x
j
Q
ij
. (17.24)
The last equation defines the components of the quadrupole moment: quadrupole
moment defined
Q
ij
=
1
2
#
Ω
V
ij
dQ(r
)=
1
2
#
Ω
(3x
i
x
j
− r
2
δ
ij
) dQ(r
). (17.25)
One can use (17.25) to calculate the quadrupole moment of any source distribution.
The quadrupole moment of electric charge distributions plays a significant role in
nuclear physics.
A scalar (function) is a tensor of type (0, 0); a contravariant vector is a
tensor of type (1, 0); a covariant vector is a tensor of type (0, 1). Similarly, the
cross product, the transformation of whose components is given in (17.19), is
atensoroftype(0, 2). Of special interest is the zero tensor, which can be of
any type. Box 17.2.1 shows clearly that
Box 17.2.2. If a tensor has zero components in one coordinate system,
it has zero components in all coordinate systems.
We have also encountered another two-indexed quantity, the Kronecker
delta. Is it a tensor? If so, what type? We may think—since we have chosen
Kronecker delta
reindexed!
both of its indices to be covariant—that it is of type (0, 2). However, that
is not the case, for the following reason. Equation (17.6), which defines the
Kronecker delta, must hold in all coordinate systems. If Kronecker delta were
of type (0, 2), then it would transform according to
¯
δ
ij
=
∂x
k
∂¯x
i
∂x
h
∂¯x
j
δ
kh
=
∂x
k
∂¯x
i
∂x
k
∂¯x
j
,
and the right-hand side does not satisfy Equation (17.6). For the same reason
the Kronecker delta cannot be a tensor of type (2, 0). What if we define it to
be a tensor of type (1, 1)? Then
¯
δ
i
j
=
∂¯x
i
∂x
k
∂x
h
∂¯x
j
δ
k
h
=
∂¯x
i
∂x
k
∂x
k
∂¯x
j
=
∂¯x
i
∂¯x
j
= δ
i
j
.

450 Tensor Anal ysi s
This shows that the proper way of indexing the Kronecker delta is to give it
one covariant and one contravariant index, i.e., to treat it as a tensor of type
(1, 1).
Example 17.2.2.
Chapter 8 introduced the idea of a four-vector, which is a
vector with four components labeled 0, 1, 2, 3, with 0 being the time component and
the rest the space components. It is common to label 4-vectors by Greek indices.the dot product in
relativity For example, x
α
represents the coordinates, u
α
= dx
α
/dτ represents the 4-velocity,
p
α
= mu
α
represents the 4-momentum, etc. The matrix η can be naturally assumed
to be a tensor η
αβ
, and the inner product of two 4-vectors a
α
and b
β
can be written
as η
αβ
a
α
b
β
, with the summation over 0, 1, 2, 3 of a repeated index (one up, one
down) understood. Because we have used i, j, k, etc., for the space part, we shall
stick to this and write, for example u
α
=(u
0
,u
i
), and
a
α
b
α
≡
3
i=0
a
α
b
α
= a
0
b
0
+ a
i
b
i
≡ a
0
b
0
+
3
i=1
a
i
b
i
.
The notation of the example above is very commonly used in relativity
theory:
Box 17.2.3. Greek indices, representing the four-dimensional spacetime,
run from 0 to 4, while Roman indices, representing the space part, run
from1to3.
17.2.1 Algebraic Properties of Tensors
In our treatment of vectors, we saw that there were some formal operations
which they obeyed. For instance, we could multiply a vector by a number,
we could add two vectors, and we could multiply two vectors to get a third
vector. Tensors also have some important properties which we summarize in
the following.
Addition
If T and S are tensors of type (r, s), then their sum U = T + S, defined
componentwise as
U
i
1
...i
r
j
1
...j
s
= T
i
1
...i
r
j
1
...j
s
+ S
i
1
...i
r
j
1
...j
s
,
is also a tensor of type (r, s). To show this, one simply has to demonstrate
that U
i
1
...i
r
j
1
...j
s
transform according to (17.20) in Box 17.2.1.
Moreover, if we define V = αT componentwise as
V
i
1
...i
r
j
1
...j
s
= αT
i
1
...i
r
j
1
...j
s
,
where α is a real number, then V isalsoatensoroftype(r, s). The combi-
nation of these two operations makes the collection of tensors of type (r, s)a
vector space.

17.2 From Vectors to Tensors 451
Multiplication
If T is a tensor of type (r
1
,s
1
)andS is a tensor of type (r
2
,s
2
), then their
tensor product U = T ⊗S, defined componentwise as
U
i
1
...i
r
1
+r
2
j
1
...j
s
1
+s
2
= T
i
1
...i
r
1
j
1
...j
s
1
S
i
r
1
+1
...i
r
1
+r
2
j
s
1
+1
...j
s
1
+s
2
(17.26)
is a tensor of type (r
1
+ r
2
,s
1
+ s
2
). For example, if T is a tensor of type
(2, 1) with components T
ij
k
and S is a tensor of type (0, 2) with components
S
lm
, then the components of their tensor product U are U
ij
klm
≡ T
ij
k
S
lm
,and
they transform according to the following rule:
U
ij
klm
= T
ij
k
S
lm
=
∂¯x
i
∂x
h
∂¯x
j
∂x
p
∂x
q
∂¯x
k
T
hp
q
∂x
r
∂¯x
l
∂x
s
∂¯x
m
S
rs
=
∂¯x
i
∂x
h
∂¯x
j
∂x
p
∂x
q
∂¯x
k
∂x
r
∂¯x
l
∂x
s
∂¯x
m
T
hp
q
S
rs
=
∂¯x
i
∂x
h
∂¯x
j
∂x
p
∂x
q
∂¯x
k
∂x
r
∂¯x
l
∂x
s
∂¯x
m
U
hp
qrs
,
which shows that U is a tensor of rank (2, 3).
Example 17.2.3.
One can obtain a tensor of any type by multiplying contravari-
ant and covariant vectors: take r contavariant vectors and s covariant vectors and
multiply them to get a tensor of type (r, s). For example, if A is a contravariant
vector with components A
i
and B a covariant vector with components B
j
,then
T
ij
≡ A
i
A
j
is a tensor of type (2, 0), S
ijk
≡ B
i
B
j
B
k
is a tensor of type (0, 3), and
U
ij
k
≡ A
i
A
j
B
k
is a tensor of type (2, 1).
Contraction
Given a tensor of type (r, s), take a covariant index and set it equal to a
contravariant index, i.e., sum over those two indices. The process is called
contraction and the end result is a tensor of type (r−1,s−1). For example,
take the tensor of type (2, 1) whose components are T
ij
k
and set k = j.How
do the components T
ij
j
transform?
T
ij
j
=
∂¯x
i
∂x
h
∂¯x
j
∂x
p
∂x
q
∂¯x
j
T
hp
q
=
∂¯x
i
∂x
h
∂x
q
∂¯x
j
∂¯x
j
∂x
p
=δ
q
p
T
hp
q
=
∂¯x
i
∂x
h
T
hq
q
.
This shows that T
ij
j
transform as components of a contravariant vector [see
Equation (17.18)], i.e., a tensor of type (1, 0).
Of special interest is a tensor of type (1, 1). When you contract this
tensor, you get a tensor of type (0, 0), i.e., a scalar. For example, let A be
a contravariant vector with components A
i
and B a covariant vector with
components B
j
.ThenT
i
j
≡ A
i
B
j
is a tensor of type (1, 1). When you
contract it, you get T
i
i
≡ A
i
B
i
, which is the dot product of the two vectors,
i.e., a scalar [see Equation (17.16)].
