Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


15.5 Problems 421
(b) In particular, show that k, the propagation direction, and E and B form
a mutually perpendicular set of vectors.
(c) By taking the cross product of k with an appropriate equation, show that
|k| = ω/c.
15.10. Derive Equation (15.34).

Chapter 16
Curvilinear Vector
Analysis
All the vector analytical quantities discussed in the previous chapters can
also be calculated in other coordinate systems. The general procedure is to
start with definitions of quantities in a coordinate-free way and substitute the
known quantities in terms of the particular coordinates we are interested in
and “read off” the vector analytic quantity. Instead of treating cylindrical and
spherical coordinate systems separately, we lump them together and derive re-
lations that hold not only in the three familiar coordinate systems, but also in
all coordinate systems whose unit vectors form a set of right-handed mutually
perpendicular vectors. Since the geometric definitions of all vector-analytic
quantities involve elements of length, we start with the length elements.
16.1 Elements of Length
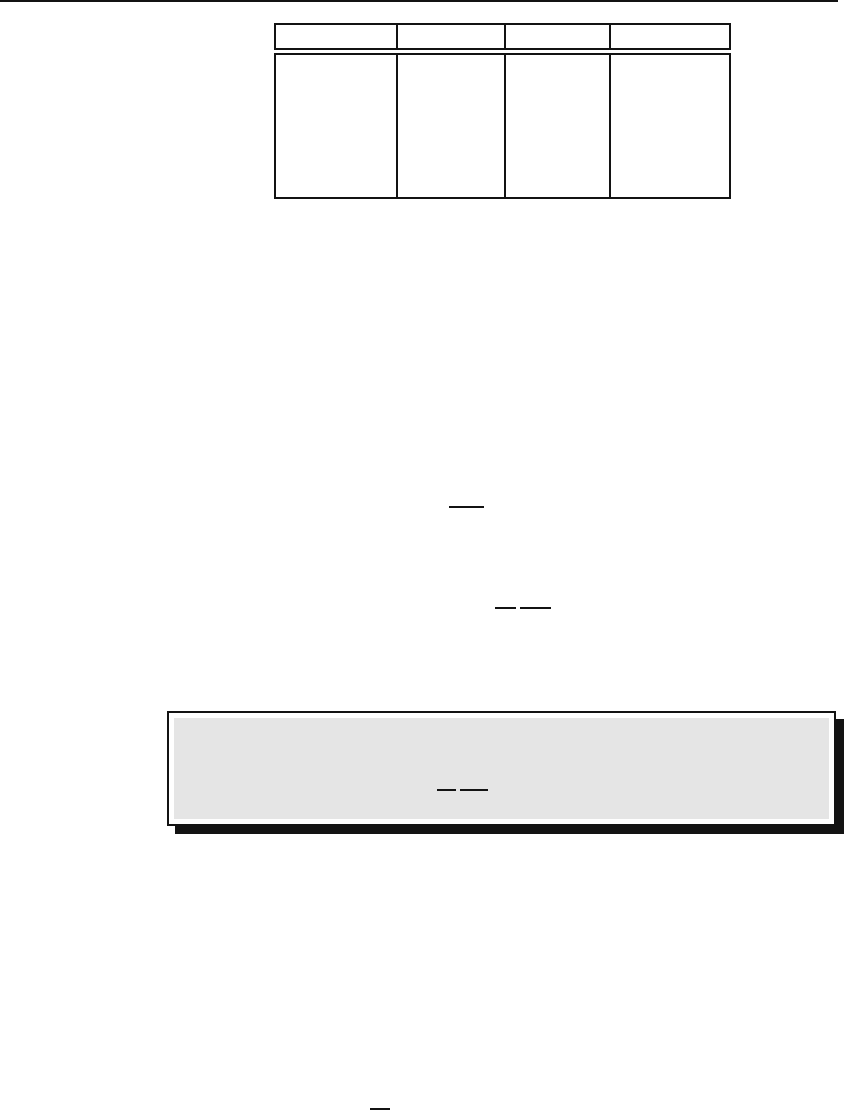
Consider curvilinear coordinates
1
(q
1
,q
2
,q
3
)inwhichtheprimary line curvilinear
coordinates
elements are given by
dl
1
= h
1
(q
1
,q
2
,q
3
) dq
1
,dl
2
= h
2
(q
1
,q
2
,q
3
) dq
2
,dl
3
= h
3
(q
1
,q
2
,q
3
) dq
3
,
where h
1
, h
2
,andh
3
are some functions of coordinates. By examining the
primary line elements in Cartesian, spherical, and cylindrical coordinates, we
can come up with Table 16.1.
Denoting the unit vectors in curvilinear coordinate systems by
ˆ
e
1
,
ˆ
e
2
,and
ˆ
e
3
, we can combine all the equations for the elements of length and write
them as a single vector equation:
dr = d
l =
ˆ
e
1
dl
1
+
ˆ
e
2
dl
2
+
ˆ
e
3
dl
3
=
ˆ
e
1
h
1
dq
1
+
ˆ
e
2
h
2
dq
2
+
ˆ
e
3
h
3
dq
3
. (16.1)
1
As will be seen shortly, Cartesian coordinates are also included in such curvilinear
coordinates. The former have lines (and planes) as their primary lengths and surfaces, thus
the word “linear” in the name of the latter.
424 Curvilinear Vector Analysis
Curvilinear Cartesian Spherical Cylindrical
q
1
x r ρ
q
2
y θ ϕ
q
3
z ϕ z
h
1
1 1 1
h
2
1 r ρ
h
3
1 r sin θ 1
Table 16.1: The specifications of the three coordinate systems in terms of curvilinear
coordinates.
This equation is useful in its own right. For example, we can obtain the curvi-
linear unit vectors as follows. Rewrite Equation (16.1) in terms of increments:
Δr ≈
ˆ
e
1
h
1
Δq
1
+
ˆ
e
2
h
2
Δq
2
+
ˆ
e
3
h
3
Δq
3
.
Keeping q
2
and q
3
constant (so that Δq
2
=0=Δq
3
), divide both sides by
Δq
1
to obtain
Δr
Δq
1
≈
ˆ
e
1
h
1
.
In the limit, the LHS becomes a partial derivative and we get
ˆ
e
1
=
1
h
1
∂r
∂q
1
. (16.2)
The other two unit vectors can be obtained similarly. We thus have
Box 16.1.1. The ith unit vector of a curvilinear coordinate system is
given by
ˆ
e
i
=
1
h
i
∂r
∂q
i
,i=1, 2, 3. (16.3)
This is a useful formula for obtaining the Cartesian components of curvilinear
unit vectors, when the Cartesian components of the position vector are given
in terms of curvilinear coordinates.
Example 16.1.1.
As an illustration of the above procedure, we calculate the unit
vectors in spherical coordinates. First we write
r = x
ˆ
e
x
+ y
ˆ
e
y
+ z
ˆ
e
z
=
ˆ
e
x
r sin θ cos ϕ +
ˆ
e
y
r sin θ sin ϕ +
ˆ
e
z
r cos θ.
Now we differentiate with respect to r to get
ˆ
e
1
≡
ˆ
e
r
=
∂r
∂r
=
ˆ
e
x
sin θ cos ϕ +
ˆ
e
y
sin θ sin ϕ +
ˆ
e
z
cos θ.

16.2 The Gradient 425
Similarly,
ˆ
e
2
≡
ˆ
e
θ
=
1
r
∂r
∂θ
=
ˆ
e
x
cos θ cos ϕ +
ˆ
e
y
cos θ sin ϕ −
ˆ
e
z
sin θ,
ˆ
e
3
≡
ˆ
e
ϕ
=
1
r sin θ
∂r
∂ϕ
= −
ˆ
e
x
sin ϕ +
ˆ
e
y
cos ϕ,
where we have used Table 16.1. These are the results we obtained in Chapter 1 from
purely geometric arguments.
We are now in a position to find the gradient, divergence, and curl of
a vector field in general curvilinear coordinates. Once these are obtained,
finding their specific forms in cylindrical and spherical coordinates entails
simply substituting the appropriate expressions for q
1
, q
2
,andq
3
and h
1
, h
2
,
and h
3
.
16.2 The Gradient
The gradient is found by equating
df =
∂f
∂q
1
dq
1
+
∂f
∂q
2
dq
2
+
∂f
∂q
3
dq
3
to the differential of f in terms of the gradient:
df = ∇f · dr =(∇f)
1
h
1
dq
1
+(∇f)
2
h
2
dq
2
+(∇f)
3
h
3
dq
3
.
The last two equations yield
(∇f)
1
h
1
=
∂f
∂q
1
, (∇f )
2
h
2
=
∂f
∂q
2
, (∇f )
3
h
3
=
∂f
∂q
3
,
which gives
gradient in
curvilinear
coordinates
Box 16.2.1. The gradient of a function f in a curvilinear coordinate
system is given by
∇f =
ˆ
e
1
1
h
1
∂f
∂q
1
+
ˆ
e
2
1
h
2
∂f
∂q
2
+
ˆ
e
3
1
h
3
∂f
∂q
3
. (16.4)
This result, in conjunction with Table 16.1, agrees with the expression ob-
tained for the gradient in the Cartesian coordinate system. In cylindrical
coordinates, we obtain
∇f =
ˆ
e
ρ
∂f
∂ρ
+
ˆ
e
ϕ
1
ρ
∂f
∂ϕ
+
ˆ
e
z
∂f
∂z
, (16.5)
426 Curvilinear Vector Analysis
so that the operator ∇ in cylindrical coordinates is given by
∇ =
ˆ
e
ρ
∂
∂ρ
+
ˆ
e
ϕ
1
ρ
∂
∂ϕ
+
ˆ
e
z
∂
∂z
. (16.6)
Similarly, in spherical coordinates, we get
gradient of a
function in
spherical
coordinates
∇f =
ˆ
e
r
∂f
∂r
+
ˆ
e
θ
1
r
∂f
∂θ
+
ˆ
e
ϕ
1
r sin θ
∂f
∂ϕ
(16.7)
with the operator ∇ given by
∇ =
ˆ
e
r
∂
∂r
+
ˆ
e
θ
1
r
∂
∂θ
+
ˆ
e
ϕ
1
r sin θ
∂
∂ϕ
. (16.8)
Example 16.2.1.
The electrostatic potential of an electric dipole was given in
Example 10.5.1 in spherical coordinates. With the expression for the gradient given
above, we can find the electric field E = −∇Φ of a dipole in spherical coordinates:
E
r
= −
∂Φ
dip
∂r
= −
∂
∂r
k
e
p cos θ
r
2
=
2k
e
p cos θ
r
3
,
E
θ
= −
1
r
∂Φ
dip
∂θ
= −
1
r
∂
∂θ
k
e
p cos θ
r
2
=
k
e
p sin θ
r
3
,
E
ϕ
= −
1
r sin θ
∂Φ
dip
∂ϕ
= −
1
r sin θ
∂
∂ϕ
k
e
p cos θ
r
2
=0.
Summarizing, we haveelectric field of an
electric dipole
E
dip
=
k
e
p
r
3
(2
ˆ
e
r
cos θ +
ˆ
e
θ
sin θ). (16.9)
This is the characteristic field of a dipole.
Example 16.2.2. Just as electric charges can produce electric dipoles, electric
currents can produce magnetic dipoles. We saw this in Subsection 15.2. In this
example, we will calculate the magnetic field of a dipole directly. Consider the
magnetic field of a circular loop of current as given in Equations (4.24) and (4.26).
We change the coordinates of the field point P to spherical and assume that P is far
away from the loop, i.e., that a is very small compared to r.Writingr
2
for ρ
2
+ z
2
and r sin θ for ρ, we expand the integrands of (4.24) and (4.26) in powers of a/r
keeping only the first nonzero power. Thus,
1
(r
2
+a
2
−2ra sin θ cos t)
3/2
=
1
r
3
1+
a
r
2
− 2
a
r
sin θ cos t
−3/2
=
1
r
3
*
1+3
a
r
sin θ cos t
+
+ ··· ,
r sin θ cos t−a
(r
2
+a
2
−2ra sin θ cos t)
3/2
=
1
r
2
sin θ cos t −
a
r
1+
a
r
2
− 2
a
r
sin θ cos t
−3/2
=
1
r
2
sin θ cos t −
a
r
*
1+3
a
r
sin θ cos t
+
+ ···
=
1
r
2
sin θ cos t −
a
r
+
3a
r
sin
2
θ cos
2
t
.

16.3 The Divergence 427
Substituting these in the integrals of (4.24) and (4.26) yields
B
ρ
=
k
m
Iaz
r
3
#
2π
0
cos t
1+
3a
r
sin θ cos t
dt =
3k
m
Iπa
2
cos θ sin θ
r
3
,
where we substituted r cos θ for z. In an analogous way, we also obtain
B
z
= −
k
m
Ia
r
2
#
2π
0
sin θ cos t −
a
r
+
3a
r
sin
2
θ cos
2
t
dt
= −
k
m
Ia
r
2
−
2πa
r
+
3aπ
r
sin
2
θ
.
We are interested in the spherical components of the magnetic field. To find
these components, we first write
B = B
ρ
ˆ
e
ρ
+ B
z
ˆ
e
z
and take the dot product with appropriate unit vectors:
B
r
= B ·
ˆ
e
r
= B
ρ
ˆ
e
ρ
·
ˆ
e
r
+ B
z
ˆ
e
z
·
ˆ
e
r
= B
ρ
sin θ + B
z
cos θ
=
3k
m
Iπa
2
cos θ sin θ
r
3
sin θ +
k
m
Ia
r
2
2πa
r
−
3aπ
r
sin
2
θ
cos θ
=
2k
m
Iπa
2
r
3
cos θ.
Similarly,
B
θ
= B ·
ˆ
e
θ
= B
ρ
ˆ
e
ρ
·
ˆ
e
θ
+ B
z
ˆ
e
z
·
ˆ
e
θ
= B
ρ
cos θ −B
z
sin θ
=
3k
m
Iπa
2
cos θ sin θ
r
3
cos θ −
k
m
Ia
r
2
2πa
r
−
3aπ
r
sin
2
θ
sin θ
=
k
m
Iπa
2
r
3
sin θ.
Summarizing, we write magnetic field of a
magnetic dipole
B =
k
m
Iπa
2
r
3
(2
ˆ
e
r
cos θ +
ˆ
e
θ
sin θ). (16.10)
This has a striking resemblance to Equation (16.9). In fact once we identify Iπa
2
as the magnetic dipole of the loop, and change all magnetic labels to electric ones,
we recover Equation (16.9).
16.3 The Divergence
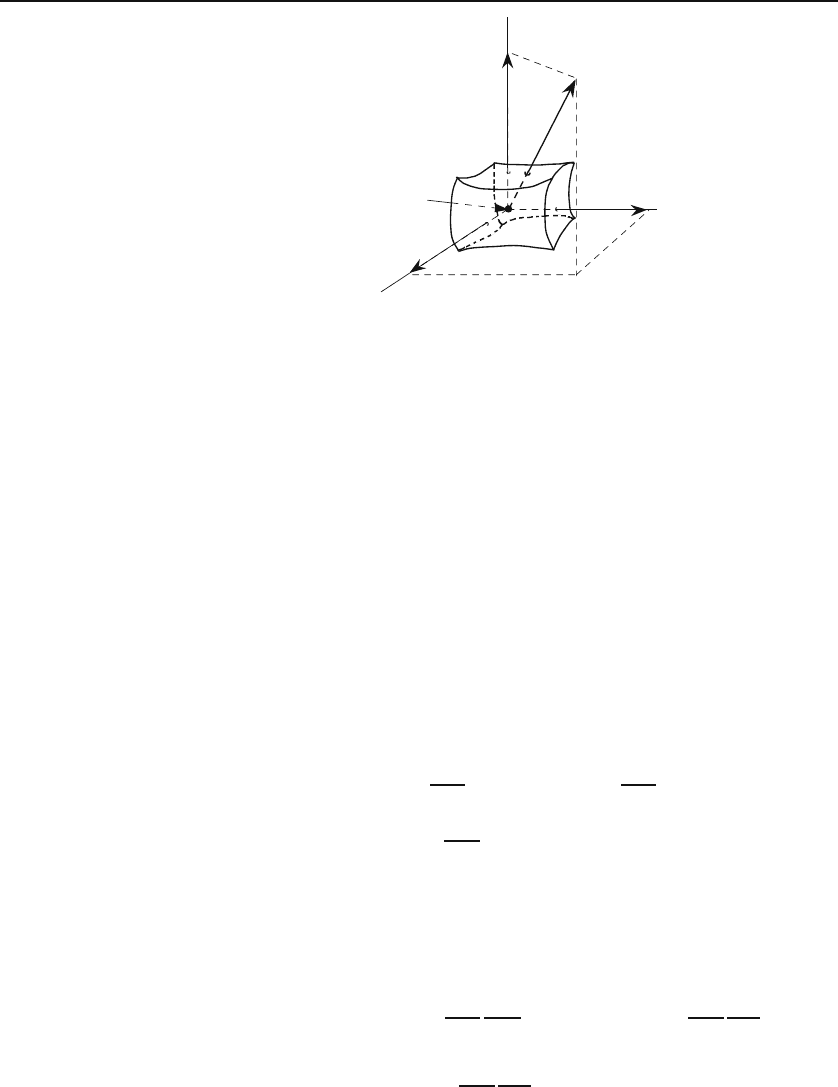
To find the divergence of a vector A, we consider the volume element of
Figure 16.1 and find the outward flux through the sides of the volume. For
the front face we have
Δφ
f
= A
f
·
ˆ
e
1
Δa
f
,
428 Curvilinear Vector Analysis
A
A
1
ˆ
e
1
A
2
ˆ
e
2
A
3
ˆ
e
3
P(q
1
, q
2
, q
3
)
Δ
Δ
Δ
l
1
l
3
l
2
Figure 16.1: Point P and the surrounding volume element in curvilinear coordinates.
Note that the midpoints of the front and back faces are Δq
1
/2 away from P in the
positive and negative
ˆ
e
1
directions, respectively. Similarly for the other four faces.
where A
f
means the value of A at the center of the front face and Δa
f
is the
area of the front face. Following the arguments presented for the Cartesian
case, we write
Δφ
f
≈ A
f
·
ˆ
e
1
Δa
f
= A
1f
Δl
2f
Δl
3f
= A
1f
(h
2
Δq
2
)
f
(h
3
Δq
3
)
f
= A
1f
h
2f
h
3f
Δq
2
Δq
3
The subscript 1 in A
1f
, for example, means component of A in the direction
of the first coordinate. The subscript f implies evaluation—at the midpoint—
on the front side whose second and third coordinates are the same as P ,and
whose first coordinate is q
1
+Δq
1
/2. Thus, we have
Δφ
f
≈ A
1
q
1
+
Δq
1
2
,q
2
,q
3
h
2
q
1
+
Δq
1
2
,q
2
,q
3
× h
3
q
1
+
Δq
1
2
,q
2
,q
3
Δq
2
Δq
3
because, unlike the Cartesian case, h
1
, h
2
,andh
3
are functions of the co-
ordinates. Using Taylor series expansion for the functions A
1
, h
2
,andh
3
yields
Δφ
f
≈
0
A
1
(q
1
,q
2
,q
3
)+
Δq
1
2
∂A
1
∂q
1
10
h
2
(q
1
,q
2
,q
3
)+
Δq
1
2
∂h
2
∂q
1
1
×
0
h
3
(q
1
,q
2
,q
3
)+
Δq
1
2
∂h
3
∂q
1
1
Δq
2
Δq
3
.
16.3 The Divergence 429
Multiplying out and keeping terms up to the third order (corresponding to
the order of a volume element by which we shall divide shortly), we obtain
Δφ
f
≈
0
A
1
h
2
h
3
+ A
1
h
2
∂h
3
∂q
1
+ A
1
h
3
∂h
2
∂q
1
+ h
2
h
3
∂A
1
∂q
1
1
Δq
1
2
Δq
2
Δq
3
=
0
A
1
h
2
h
3
+
∂
∂q
1
(h
2
h
3
A
1
)
1
Δq
1
2
Δq
2
Δq
3
,
where we left out the explicit dependence of the functions on their independent
coordinate variables. For the back face we have
Δφ
b
≈ A
b
· (−
ˆ
e
1
Δa
b
)=−A
1b
Δl
2b
Δl
3b
= −A
1b
(h
2
Δq
2
)
b
(h
3
Δq
3
)
b
= −A
1
q
1
−
Δq
1
2
,q
2
,q
3
h
2
q
1
−
Δq
1
2
,q
2
,q
3
× h
3
q
1
−
Δq
1
2
,q
2
,q
3
Δq
2
Δq
3
.
Taylor expanding the three functions A
1
, h
2
,andh
3
as above, and multiplying
out yields
Δφ
b
≈−
0
A
1
h
2
h
3
−
∂
∂q
1
(h
2
h
3
A
1
)
1
Δq
1
2
Δq
2
Δq
3
.
Adding the front and back contributions, we obtain
Δφ
1
≡ Δφ
f
+Δφ
b
≈
∂
∂q
1
(h
2
h
3
A
1
)Δq
1
Δq
2
Δq
3
.
Similarly, the fluxes through the faces perpendicular to
ˆ
e
2
and
ˆ
e
3
are
Δφ
2
≈
∂
∂q
2
(h
1
h
3
A
2
)Δq
1
Δq
2
Δq
3
,
Δφ
3
≈
∂
∂q
3
(h
1
h
2
A
3
)Δq
1
Δq
2
Δq
3
. (16.11)
Adding the three contributions and dividing by the volume
ΔV =Δl
1
Δl
2
Δl
3
= h
1
h
2
h
3
Δq
1
Δq
2
Δq
3
and finally taking the limit of smaller and smaller volumes—which turns all
approximations into equalities—we get
divergence in
curvilinear
coordinates
Theorem 16.3.1. The divergence of a vector field A in a curvilinear coordi-
nate system is given by
∇ · A =
1
h
1
h
2
h
3
0
∂
∂q
1
(h
2
h
3
A
1
)+
∂
∂q
2
(h
1
h
3
A
2
)+
∂
∂q
3
(h
1
h
2
A
3
)
1
.
430 Curvilinear Vector Analysis
Now that we have a general formula for the divergence, we can use Table
16.1 to write the divergence in a specific coordinate system. For instance,
substituting the entries of the second column gives the formula in Theorem
13.2.1, and the third column yields
divergence of a
vector field in
spherical
coordinates
∇ · A =
1
r
2
sin θ
(
∂
∂r
r
2
sin θA
r
!
+
∂
∂θ
(r sin θA
θ
)+
∂
∂ϕ
(rA
ϕ
)
)
=
1
r
2
∂
∂r
r
2
A
r
!
+
1
r sin θ
0
∂
∂θ
(sin θA
θ
)+
∂A
ϕ
∂ϕ
1
. (16.12)
To obtain the divergence in cylindrical coordinates, we use the last column
and obtain
∇ · A =
1
ρ
0
∂
∂ρ
(ρA
ρ
)+
∂
∂ϕ
(A
ϕ
)+
∂
∂z
(ρA
z
)
1
=
1
ρ
∂
∂ρ
(ρA
ρ
)+
1
ρ
∂A
ϕ
∂ϕ
+
∂A
z
∂z
. (16.13)
Example 16.3.2.
Consider the vector field defined by
A = kr
α
ˆ
e
r
,
where k and α are constants. Let us verify the divergence theorem for a spherical
surface of radius R (see Figure 16.2). The total flux is obtained by integrating over
the surface of the sphere:
φ =
##
S
A · da =
##
S
kR
α
ˆ
e
r
·
ˆ
e
n
R
2
sin θdθdϕ
= kR
α+2
##
S
sin θdθdϕ=4πkR
α+2
.
d
θ
d
ϕ
ˆ
e
n
=
ˆ
e
r
R
x
y
z
Figure 16.2: The element of area and its unit normal for a sphere.

16.4 The Curl 431
On the other hand, using the expression for divergence in the spherical coordinate
system and noting that A
θ
=0=A
ϕ
,weobtain
∇ · A =
1
r
2
∂
∂r
(r
2
A
r
)=
1
r
2
d
dr
kr
α+2
!
=(α +2)kr
α−1
,
wherewehaveassumedthatα = −2. Therefore,
##
V
#
∇ · A dV =
#
R
0
(α +2)kr
α−1
r
2
dr
#
π
0
sin θdθ
#
2π
0
dϕ =4πkR
α+2
which agrees with the surface integration.
For α = −2 the divergence appears to vanish everywhere. However, a closer
examination reveals that the statement is true only if r = 0. In fact, as we discussed
before, the divergence of A is proportional to the Dirac delta function, δ(r)inthis
case [see Equation (15.2)].
16.4 The Curl
To calculate the curl, we choose a closed path perpendicular to one of the unit
vectors, say
ˆ
e
1
and calculate the line integral of A around it. The situation is
depicted in Figure 16.3. We calculate the contribution to the line integral from
path (1) in detail and leave calculation of contributions from the remaining
three paths to the reader. In all calculations, terms of higher order than the
second will be omitted
#
(1)
A · dr ≈ A
l
· Δr
l
= A
l
·(−
ˆ
e
3
Δl
l
)=−A
3l
Δl
l
= −A
3l
h
3l
Δq
3
= −A
3
q
1
,q
2
−
Δq
2
2
,q
3
h
3
q
1
,q
2
−
Δq
2
2
,q
3
Δq
3
= −
(
A
3
−
Δq
2
2
∂A
3
∂q
2
)(
h
3
−
Δq
2
2
∂h
3
∂q
2
)
Δq
3
≈−A
3
h
3
Δq
3
+
∂
∂q
2
(h
3
A
3
)
Δq
2
2
Δq
3
.
P
(
q
1
,
q
2
,
q
3
)
(1)
(2)
(3)
(4)
h
2
b
dq
2
h
2
t
dq
2
h
3
l
dq
3
h
3
r
dq
3
ˆ
e
2
ˆ
e
3
ˆ
e
1
Figure 16.3: Path of integration for the first component of the curl of A in curvilinear
coordinates.
