Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

14.2 Curl of a Vector Field and Stokes’ Theorem 391

Many a time parameterization makes life a lot easier! Suppose we want parameterization

is essential for

obtaining the

correct sign for

some line

integrals!

to calculate the line integral of a vector ﬁeld along path (iv) of Figure 14.3.

First let us attempt to calculate the line integral using the coordinates. Along

path (iv) dr = −

dx;soA ·dr = −A

dx.Then

(0,a)

(a,a)

A · dr = −

dx =

dx.

Thus, if A

> 0 (try A

= x

), the integral will be positive. But this is wrong:

A positive A

should yield a negative A · dr because the two vectors are in

opposite directions!

With parameterization, this problem is alleviated. A parameterization

that represents path (iv) is

x = a(1 − t),y= a, 0 ≤ t ≤ 1.

Clearly, t = 0 corresponds to the beginning of path (iv) and t =1toits

endpoint. The parameterization automatically gives dx = −adt and dy =0.

For instance, the vector ﬁeld of Example 14.1.2 yields

(0,a)

(a,a)

A · dr =

a(1 −t)a

(−adt)=−a

(1 −t) dt = −

This has the correct sign because A

is positive and the direction of integration

negative. The other method would have given a positive result!

14.2 Curl of a Vector Field and Stokes’

Theorem

Line integrals around a closed path are of special interest. For example, if

the velocity vector of a ﬂuid has a nonzero integral around a closed path, the

ﬂuid must be turning around that path and a whirlpool must reside inside

the closed path. It is remarkable that such a mundanely concrete idea can be

applied verbatim to much more abstract and sophisticated concepts such as

electromagnetic ﬁelds with proven success and relevance. Thus, for a vector

ﬁeld, A, and a closed path, C,wedenotethelineintegralas

A ·dr

where the circle on the integral sign indicates that the path is closed and C

denotes the particular path taken.

In our discussion of divergence and ﬂux, we encountered Equation (13.11)

where an integral (over volume V ) was related to an integral over its boundary

(surface S). This remarkable property has an analog in one lower dimension:

Any closed curve bounds a surface inside it. Is it possible to connect the

392 Line Integral and Curl

Figure 14.4: There is no “the” surface having C as its boundary. Both S

and S

—as

well as a multitude of others—are such surfaces.

line integral over the closed curve to a surface integral over the surface? The

answer is yes, but we have to be careful here. What do we mean by “the” sur-

face? A given closed curve may bound many diﬀerent surfaces, as Figure 14.4

shows. It turns out that this freedom, which was absent in the divergence

case,

is irrelevant and the relation holds for any surface whose boundary is

the given curve.

Let us now develop the analog of the divergence theorem for closed line

integrals. To begin, we consider a small closed rectangular path with a unit

normal

, which is related to the direction of traversing the path by the

right-hand rule (RHR):

Right-hand rule

(RHR) rules here!

Box 14.2.1. (The Right-Hand Rule). Curl the ﬁngers of your right

hand in the direction of integration along the curve, your thumb should

then point in the direction of

Without loss of generality we assume that the rectangle is parallel to the xy-

plane with sides parallel to the x-axis and the y-axis and that

is parallel

to the z-axis (see Figure 14.5). The line integral can be written as

A · dr =

A ·dr +

A ·dr.

We do the ﬁrst integral in detail; the rest are similar. Along ab the element

of displacement dr is always in the positive x-direction and has magnitude dx,

It should be clear that we cannot change the shape of the volume enclosed in S without

changing S itself. This rigidity is due to the maximality of the dimension of the enclosed

region: A volume is a three-dimensional object, and three is the maximum dimension we

have. Theories with higher dimension than three will allow a deformability similar to the

one discussed above.

14.2 Curl of a Vector Field and Stokes’ Theorem 393

Δ y

z ˆ

Figure 14.5: A closed rectangular path parallel to the xy-plane with center at (x, y, z).

soitcanbewrittenasdr =

dx. Thus, the ﬁrst integral on the RHS above

becomes

A ·dr ≡

·dr

·(

dx)=

dx,

where, as before, the subscript 1 indicates that we have to evaluate A at the

midpoint of ab and the subscript x denotes the x-component. Now, since ab

is small and the angle between A and dr does not change appreciably on ab,

we can approximate the integral with A

ab and write

A ·dr ≈ A

ab = A

Δx = A



x, y −

Δy





 

coordinates of

midpoint of

Δx

≈

(

(x, y, z) −

Δy

∂A

∂y

)

Δx,

where in the last line we used the Taylor expansion of A

. Similarly, we can

write

A · dr =

·dr

· (−

dx)=−

≈−A

cd = −A

Δx = −A



x, y +

Δy





 

coordinates of

midpoint of

Δx

≈−

(

(x, y, z)+

Δy

∂A

∂y

)

Δx.

Adding the contributions from sides ab and cd yields

A · d r +

A ·dr ≈−

∂A

∂y

Δx Δy.

This condition is essential, because a rapidly changing angle implies a rapidly changing

component A

which is not suitable for the approximation to follow.

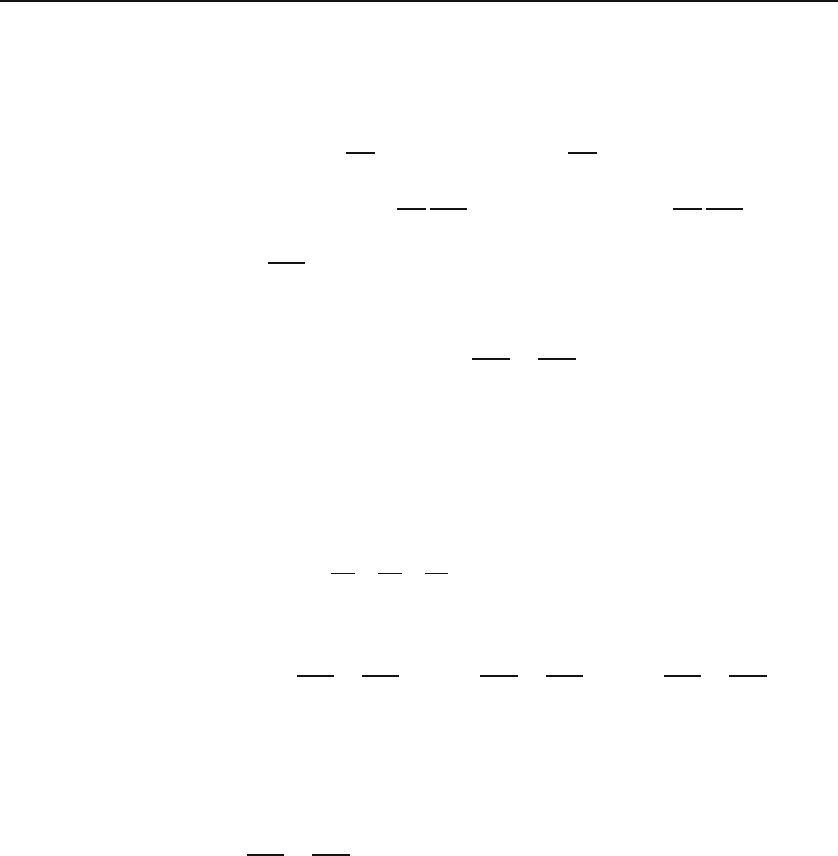
394 Line Integral and Curl

The contributions from the other two sides of the rectangle can also be

calculated:

A ·dr +

A ·dr ≈ A

Δy − A

Δy

= A



x +

Δx

,y,z



Δy − A



x −

Δx

,y,z



Δy

≈

(

(x, y, z)+

Δx

∂A

∂x

)

Δy −

(

(x, y, z) −

Δx

∂A

∂x

)

Δy

∂A

∂x

Δx Δy.

The sum of these two equations gives the total contribution:

A ·d r ≈



∂A

∂x

−

∂A

∂y



Δx Δy. (14.3)

Let us look at Equation (14.3) more closely. The expression in parentheses

can be interpreted as the z-component of the cross product of the gradient

operator ∇ with A. In fact, using the mnemonic determinant form of the

vector product, we can write

∇ × A =det

⎛

⎜

⎝

∂

∂x

∂

∂y

∂

∂z

⎞

⎟

⎠



∂A

∂y

−

∂A

∂z





∂A

∂z

−

∂A

∂x





∂A

∂x

−

∂A

∂y



This cross product is called the curl of A and is an important quantity in

curl of a vector

ﬁeld deﬁned

vector analysis. We will look more closely at it later. At this point, however,

we are interested only in its deﬁnition as applied in Equation (14.3). The

RHS of that equation can be written as



∂A

∂x

−

∂A

∂y



Δx Δy =(∇ ×A)

Δx Δy =(∇ ×A) ·

Δa,

where Δa =Δx Δy is the area of the rectangle. Noting that

is in the

direction normal to the area, we can replace it with

. Therefore, we can

write Equation (14.3) as

A ·dr ≈ (∇× A) ·

Δa =(∇ ×A) ·Δa. (14.4)

Equation (14.4) states that for a small rectangular path C the closed line

integral is equal to the normal component of the curl of A evaluated at the

center of the rectangle times the area of the rectangle. This statement does

14.2 Curl of a Vector Field and Stokes’ Theorem 395

not depend on the choice of coordinate system. In fact, any rectangle (or any

closed planar loop) deﬁnes a plane and we are at liberty to designate that

plane the xy-plane. Thus, we can deﬁne the curl of a vector ﬁeld this way:

coordinate

independent

deﬁnition of curl

Deﬁnition 14.2.1. Given a small closed curve C, calculate the line integral

of A around it and divide the result by the area enclosed by C. The component

of the curl of A along the unit normal to the area is given by

Curl A ·

≡ ∇ ×A ·

= lim

Δa→0

A ·dr

Δa

. (14.5)

The direction of

is related to the sense of integration via the right-hand

rule.

In Equation (14.5) we are assuming that the area is ﬂat. This is always

possible by taking the curve small enough. Deﬁnition 14.2.1 is completely

independent of the coordinate system and we shall use it to derive expressions

for the curl of vector ﬁelds in spherical and cylindrical coordinates as well.

The reader should be aware that the notation ∇×A is just that, a notation,

and—except in Cartesian coordinates—should not be considered as a cross

product.

What happens with a large closed path? Figure 14.6 shows a closed path C

from small

rectangles to large

loops

with an arbitrary surface S, whose boundary is the given curve. We divide S

into small rectangular areas and assign a direction to their contours dictated

by the direction of integration around C.

If we sum all the contributions

from the small rectangular paths, we will be left with the integration around

C because the contributions from the common sides of adjacent rectangles

cancel.

This is because the sense of integration along their common side is

Figure 14.6: An arbitrary surface with the curve C as its boundary. The sum of the

line integrals around the rectangular paths shown is equal to the line integral around C.

The direction of the contour with one side on the curve C is determined by the direction

of the integration of C. The direction of a distant contour is determined by working one’s

way to it one (small) rectangle at a time.

This situation is completely analogous to the calculation of the total ﬂux in the deriva-

tion of the divergence theorem.

396 Line Integral and Curl

opposite for two adjacent rectangles (see Figure 14.6). Thus, the macroscopic

version of Equation (14.4) is

A · dr ≈



i=1

(∇× A)

Δa



i=1

(∇× A)

·Δa

where (∇× A)

is the curl of A evaluated at the center of the ith rectangle,

which has area Δa

and normal

,andN is the number of rectangles on

the surface S. If the areas become smaller and smaller as N gets larger and

larger, we can replace the summation by an integral and obtain

the most

important Stokes’

theorem

Theorem 14.2.1. (Stokes’ Theorem). The line integral of a vector ﬁeld

A around a closed path C is equal to the surface integral of the curl of A on

any surface whose only edge is C. In mathematical symbols, we have

A · dr =

∇ × A ·da. (14.6)

The direction of the normal to the inﬁnitesimal area da of the surface S is

related to the direction of integration around C by the right-hand rule.

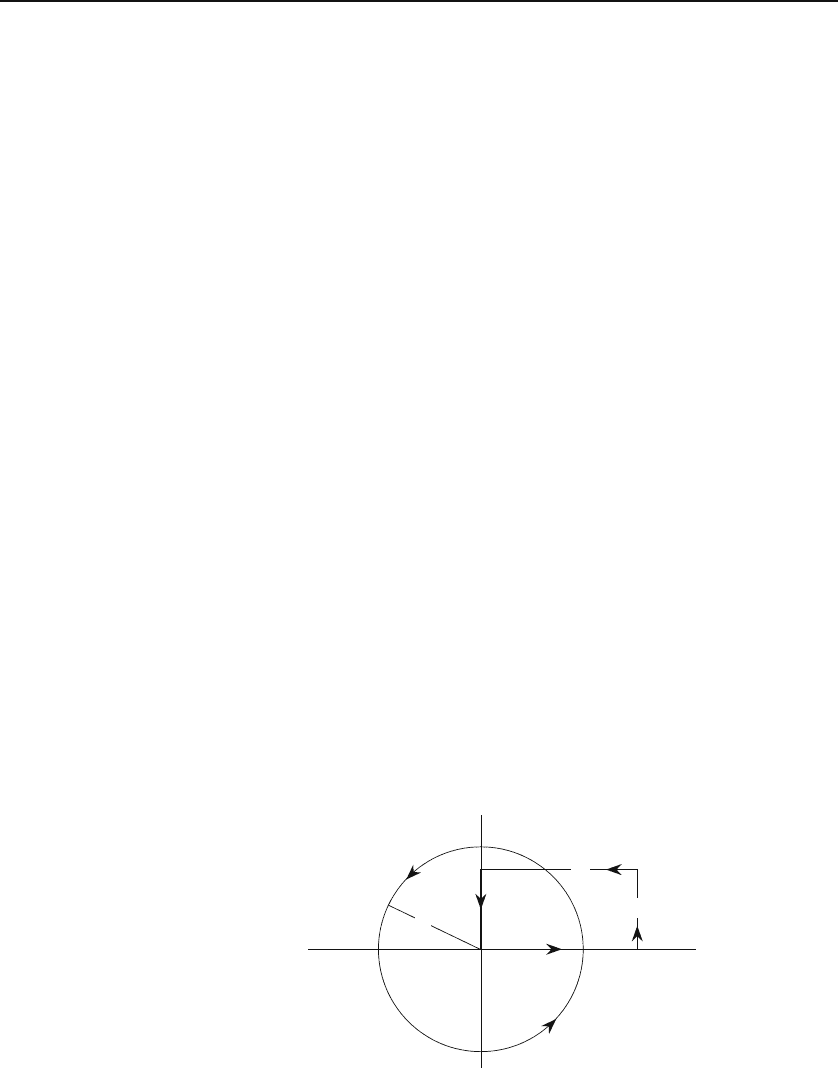
Example 14.2.2.

In this example we apply the concepts of closed line integral

and the Stokes’ theorem to a concrete vector ﬁeld. Consider the vector ﬁeld

A = K(x

+ xy

)

obtained from the vector ﬁeld of Example 14.1.2 by switching the x-andy-components.

We want to calculate the line integral around the two closed loops (the circle and

the rectangle) of Figure 14.7 and verify the Stokes’ theorem.

A convenient parameterization for the circle is

x = a cos t, y = a sin t, 0 ≤ t ≤ 2π,

with dx = −a sin tdt and dy = a cos tdt.Thus,

A · dr = K(a cos t)

(a sin t)(−a sin tdt)+K(a cos t)(a sin t)

(a cos tdt)=0,

Figure 14.7: Two loops around which the vector ﬁeld of Example 14.2.2 is calculated.

14.2 Curl of a Vector Field and Stokes’ Theorem 397

and the LHS of the Stokes’ theorem is zero. For the RHS, we need the curl of the

vector.

∇ ×A = K



∂

∂x

∂

∂y

∂

∂z

yxy



= K(y

− x

)

It is convenient to use cylindrical coordinates for integration over the area of the

circle. Moreover, the right-hand rule determines the unit normal to the area of the

circle to be

.Thus,

∇ × A ·da = K

2π

(ρ

sin

ϕ − ρ

cos

ϕ)ρdρdϕ =0

by the ϕ integration. Thus the two sides of the Stokes’ theorem agree.

The two sides of the rectangular loop sitting on the axes will give zero because

A = 0 there. The contribution of the side parallel to the y-axis can be obtained by

noting that x =2b and dx =0,sothat

A · dr = A

dx + A

dy =0+2bKy

and

(2b,b)

(2b,0)

A · dr =2bK

dy =

To avoid ambiguity,

we employ parameterization for the last line integral. A con-

venient parametric equation would be

x =2b(1 − t),y= b, 0 ≤ t ≤ 1,

which gives dx = −2bdt, dy = 0, and for which the line integral yields

(2b,0)

(2b,b)

A · dr = K

[2b(1 − t)]

(b)(−2bdt)=−8b

(1 − t)

dt = −

So, the line integral for the entire loop (the LHS of the Stokes’ theorem) is

A · dr =

−

= −2Kb

We have already calculated the curl of A. Thus, the RHS of the Stokes’ theorem

becomes

∇ ×A · da = K

− x

) dx dy

= K



 

=2b(b

/3)

−K



 

(8b

/3)b

= −2Kb

and the two sides agree.



See the discussion following Example 14.1.2.

398 Line Integral and Curl

Historical Notes

George Gabriel Stokes published papers on the motion of incompressible ﬂuids in

1842–43 and on the friction of ﬂuids in motion, and on the equilibrium and motion

of elastic solids in 1845.

In 1849 Stokes was appointed Lucasian Professor of Mathematics at Cambridge,

and in 1851 he was elected to the Royal Society and was secretary of the society

from 1854 to 1884 when he was elected president.

He investigated the wave theory of light, named and explained the phenomenon

of ﬂuorescence in 1852, and in 1854 theorized an explanation of the Fraunhofer lines

in the solar spectrum. He suggested these were caused by atoms in the outer layers

of the Sun absorbing certain wavelengths. However, when Kirchhoﬀ later published

this explanation, Stokes disclaimed any prior discovery.

George Gabriel

Stokes 1819–1903

Stokes developed mathematical techniques for application to physical problems

including the most important theorem which bears his name. He founded the science

of geodesy, and greatly advanced the study of mathematical physics in England. His

mathematical and physical papers were published in ﬁve volumes, the ﬁrst three of

which Stokes edited himself in 1880, 1883, and 1891. The last two were edited by

Sir Joseph Larmor in 1887 and 1891.

14.3 Conservative Vector Fields

Of great importance are conservative vector ﬁelds, which are those vec-

tor ﬁelds that have vanishing line integrals around every closed path. An

immediate result of this property is that

conservative

vector ﬁelds

deﬁned

Box 14.3.1. The line integral of a conservative vector ﬁeld between two

arbitrary points in space is independent of the path taken.

To see this, take any two points P

and P

connected by two diﬀerent directed

paths C

and C

as shown in Figure 14.8(a). The combination of C

and the

negative of C

forms a closed loop [Figure 14.8(b)] for which we can write

A ·dr +

−C

A ·dr =0

because A is conservative by assumption. The second integral is the negative

of the integral along C

. Thus, the above equation is equivalent to

A ·dr −

A · dr =0 ⇒

A ·dr =

A · dr

which proves the above claim.

Now take an arbitrary reference point P

and connect it via arbitrary paths

to all points in space. At each point P with Cartesian coordinates (x, y, z),

deﬁne the function Φ(x, y, z)by

Φ(x, y, z)=−

A ·dr ≡−

A · dr, (14.7)

14.3 Conservative Vector Fields 399

− C

)b()a(

Figure 14.8: (a) Two paths from P

to P

, and (b) the loop formed by them.

where C is any path from P

to P andtheminussignisintroducedfor the function Φ,so

deﬁned, has the

mathematical

property expected

of a function,

namely, that for

every point P ,the

function has only

one value that we

may denote as

Φ(P ).

historical reasons only. Φ is a well-deﬁned function because its value does not

depend on C and is called the potential associated with the vector ﬁeld A.

We note that the potential at P

is zero. That is why P

is called the potential

reference point.

Now consider two arbitrary points P

and P

, with Cartesian coordinates

)and(x

), connected by some path C. We can also connect

these two points by a path that goes from P

to P

and then to P

(see

Figure 14.9). Since A is conservative, we have

A ·dr =

A ·dr +

A · dr =Φ(x

) − Φ(x

)

potential of a

conservative

vector ﬁeld

Φ(x

) −Φ(x

)=−

A · dr, (14.8)

which expresses the potential diﬀerence between the two points.

If P

and P

are displaced inﬁnitesimally by dr, then their inﬁnitesimal

potential diﬀerence will be

dΦ=−A · dr.

On the other hand, Φ, being a scalar diﬀerentiable function of x, y,andz,has

inﬁnitesimal increment

dΦ=

∂Φ

∂x

dx +

∂Φ

∂y

dy +

∂Φ

∂z

dz =(∇Φ) ·dr,

Figure 14.9: Any path C from P

to P

is equivalent to the path P

→ P

400 Line Integral and Curl

so we have

−A · dr =(∇Φ) · dr.

But this is true for an arbitrary dr.Takingdr to be

dx,

dy,and

in turn, we obtain the equality of the three components of ∇Φand−A.

Therefore, we have

A = −∇Φ, (14.9)

which states that

Theorem 14.3.1. A conservative vector ﬁeld can be written as the negative

gradient of a potential function deﬁned as

Φ(x, y, z)=−

A ·dr,

where (x, y, z) are the coordinates of P , and the integral is taken along any

path connecting P

and P .

Another property of a conservative vector ﬁeld can be obtained by rewrit-

ing Equation (14.4), which is true for an arbitrary inﬁnitesimal closed path:

A ·dr ≈ (∇× A) ·

Δa.

However, the LHS is zero because A is conservative. Thus we have

the curl of a

conservative

vector ﬁeld is zero.

(∇× A) ·

Δa =0.

This is true for arbitrary Δa and

. Therefore, we have the important

conclusion that ∇ × A = 0 for a conservative vector ﬁeld. It is important to

note that although

A · dr is zero and C is small, we cannot deduce that

A · dr = 0 and, therefore, A =0. (Why?)

A conservative vector ﬁeld demands the vanishing of the curl. But is∇ × A =0does

not necessarily

imply that A is

conservative!

∇ × A =0suﬃcientforA to be conservative? The answer, in general, is

no! (See Example 14.3.3 below.) If the vector ﬁeld is well deﬁned and well

behaved (smoothly varying, diﬀerentiable, etc.) in a region of space U ,then

∇×A =0inU implies that

A·dr = 0 for all closed curves C lying entirely

in U. In modern mathematical jargon such a region is said to be contractible

to zero, which means that any closed curve in U can be contracted to a point

(or “zero” closed curve) without encountering any singular point of the vector

ﬁeld (where it is not deﬁned or well behaved). We state this result as follows:

Box 14.3.2. Let the region U in space be contractible to zero for the vector

ﬁeld A. Then for any closed curve C in U, the two relations ∇ × A =0

and

A · dr =0are equivalent.