Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

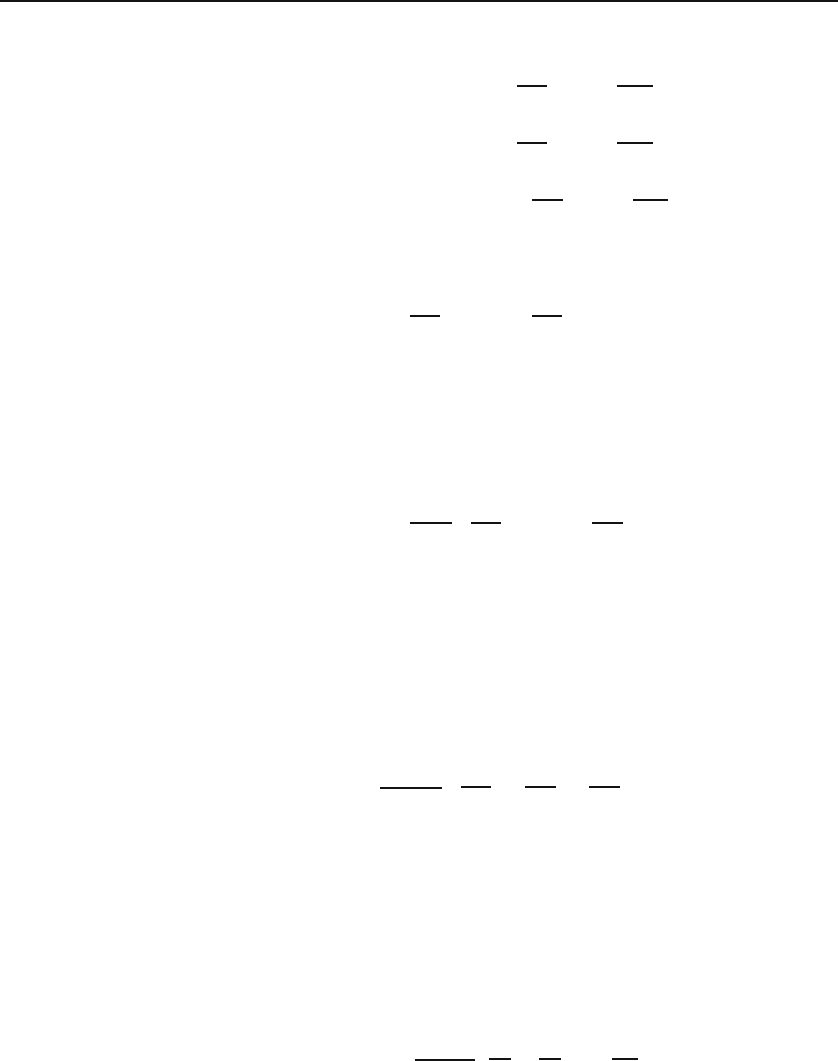
432 Curvilinear Vector Analysis
Following similar steps, the reader may check that
#
(2)
A · dr ≈ A
3
h
3
Δq
3
+
∂
∂q
2
(h
3
A
3
)
Δq
2
2
Δq
3
,
#
(3)
A · dr ≈ A
2
h
2
Δq
2
−
∂
∂q
3
(h
2
A
2
)
Δq
3
2
Δq
2
, (16.14)
#
(4)
A · dr ≈−A
2
h
2
Δq
2
−
∂
∂q
3
(h
2
A
2
)
Δq
3
2
Δq
2
.
Summing up all these contributions, we obtain
2
A · dr ≈
(
∂
∂q
2
(h
3
A
3
) −
∂
∂q
3
(h
2
A
2
)
)
Δq
2
Δq
3
.
Dividing this by the area enclosed by the path
Δa =Δl
2
Δl
3
= h
2
h
3
Δq
2
Δq
3
we obtain the first component, the component along the unit normal to the
area:
(∇× A)
1
=
1
h
2
h
3
(
∂
∂q
2
(h
3
A
3
) −
∂
∂q
3
(h
2
A
2
)
)
.
Corresponding expressions for the other two components of the curl can
be found by proceeding as above. We can put all of the components together
in a mnemonic determinant form:
curl in curvilinear
coordinates
Theorem 16.4.1. The curl of a vector field A in a curvilinear coordinate
system is given by
∇ × A =
1
h
1
h
2
h
3
ˆ
e
1
h
1
ˆ
e
2
h
2
ˆ
e
3
h
3
∂
∂q
1
∂
∂q
2
∂
∂q
3
h
1
A
1
h
2
A
2
h
3
A
3
. (16.15)
Note that ∇×A is not a cross product (except in Cartesian coordinates),
warning! ∇ ×A is
not across
product in general
curvilinear
coordinates!
but a vector defined by the determinant on the RHS of (16.15).
If we substitute the appropriate values for h’s and q’s in spherical coordi-
nates, we obtain
∇ × A =
1
r
2
sin θ
ˆ
e
r
ˆ
e
θ
r
ˆ
e
ϕ
r sin θ
∂
∂r
∂
∂θ
∂
∂ϕ
A
r
rA
θ
r sin θA
ϕ
. (16.16)
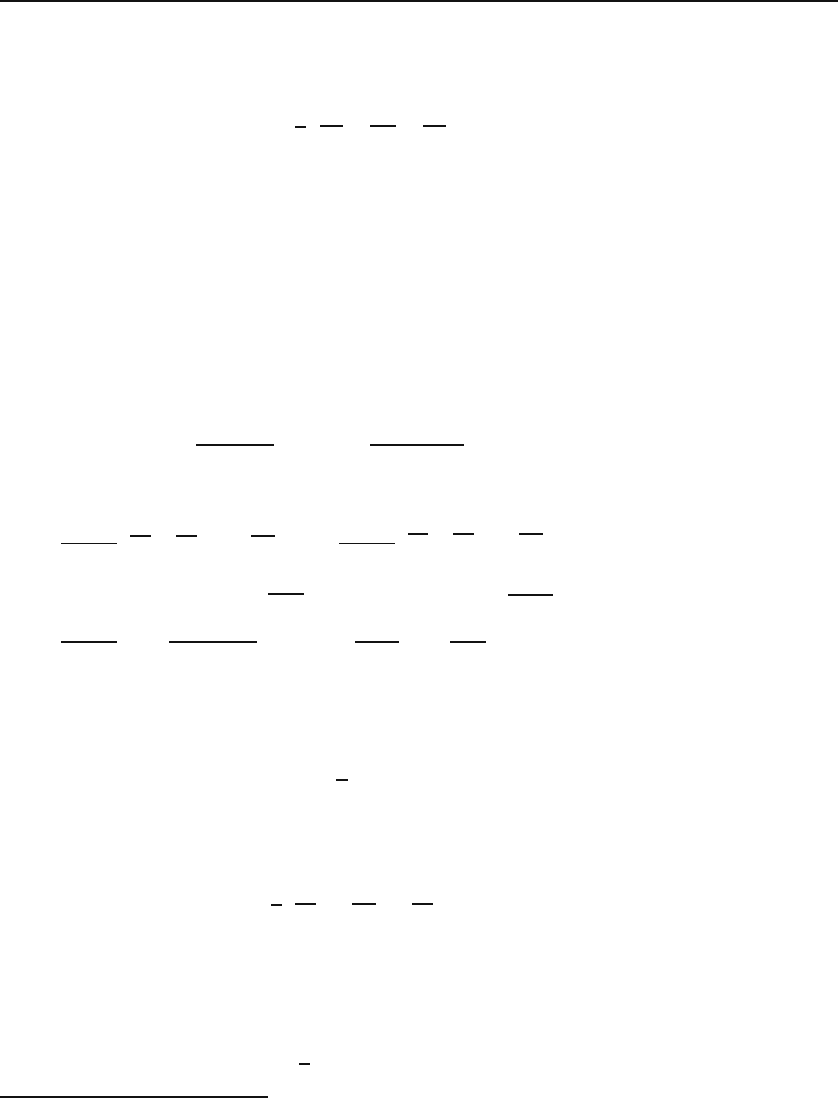
16.4 The Curl 433
In cylindrical coordinates we get
∇ × A =
1
ρ
ˆ
e
ρ
ˆ
e
ϕ
ρ
ˆ
e
z
∂
∂ρ
∂
∂ϕ
∂
∂z
A
ρ
ρA
ϕ
A
z
. (16.17)
Example 16.4.2.
We have already calculated the magnetic field of a dipole in
Example 16.2.2. Here we want to obtain the same result using the vector potential
of a dipole given in Equation (15.12). We take μ to be along the z-axis. Then
μ = μ
ˆ
e
z
= μ(
ˆ
e
r
cos θ −
ˆ
e
θ
sin θ)
and
μ ×
ˆ
e
r
= μ(−sin θ
ˆ
e
θ
×
ˆ
e
r
)=μ sin θ
ˆ
e
ϕ
.
Therefore,
B = ∇ × A = ∇ ×
k
m
μ ×
ˆ
e
r
r
2
= ∇ ×
k
m
μ sin θ
ˆ
e
ϕ
r
2
=
k
m
μ
r
2
sin θ
ˆ
e
r
ˆ
e
θ
r
ˆ
e
ϕ
r sin θ
∂
∂r
∂
∂θ
∂
∂ϕ
00r sin θ
sin θ
r
2
=
k
m
μ
r
2
sin θ
ˆ
e
r
ˆ
e
θ
r
ˆ
e
ϕ
r sin θ
∂
∂r
∂
∂θ
∂
∂ϕ
00
sin
2
θ
r
=
k
m
μ
r
2
sin θ
ˆ
e
r
2sinθ cos θ
r
− r
ˆ
e
θ
−
sin
2
θ
r
2
=
k
m
μ
r
3
(2 cos θ
ˆ
e
r
+sinθ
ˆ
e
θ
),
which is the expression obtained in Example 16.2.2.
Example 16.4.3. Consider the vector field B described in cylindrical coordinates
as
B =
k
ρ
ˆ
e
ϕ
,
where k is a constant. The curl of B is easily found to be zero:
∇ × B =
1
ρ
ˆ
e
ρ
ˆ
e
ϕ
ρ
ˆ
e
z
∂
∂ρ
∂
∂ϕ
∂
∂z
0 ρ(k/ρ)0
=0.
However, for any circle (of radius a, for example) centered at the origin and located
in the xy-plane, we get
2
2
C
B · dr =
#
2π
0
k
a
ˆ
e
ϕ
· (
ˆ
e
ϕ
adϕ)=2πk =0.
2
See also Example 14.3.3 which discusses this same vector field in Cartesian coordinates.
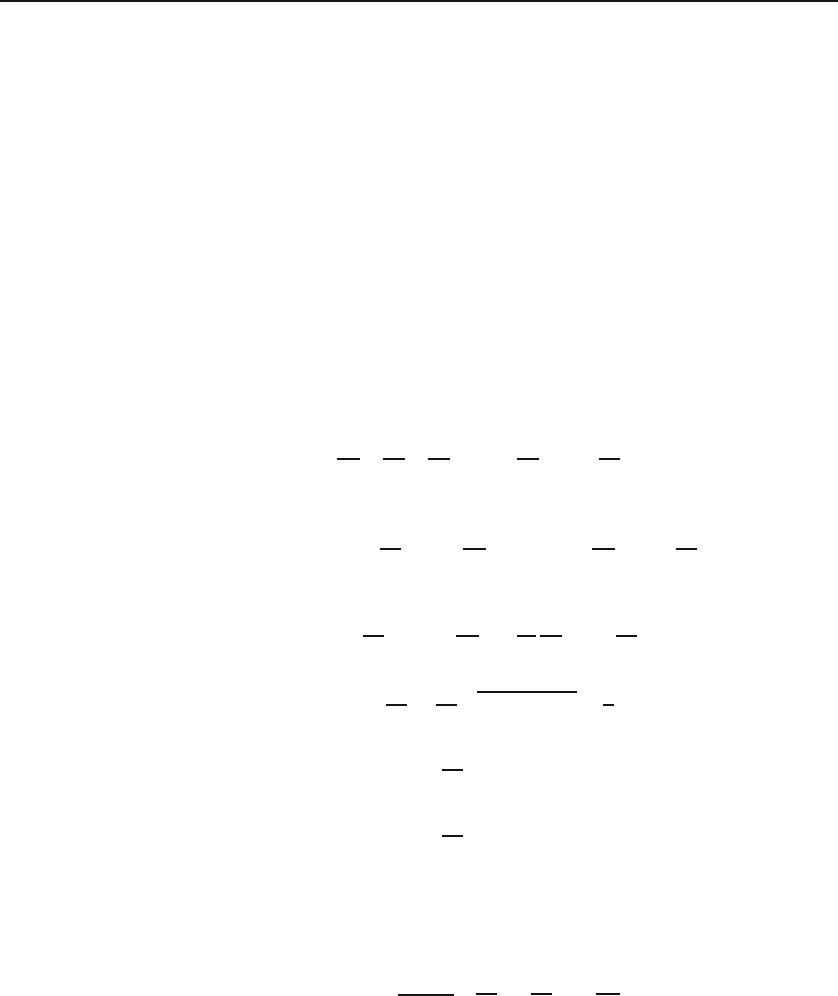
434 Curvilinear Vector Analysis
The reason for this result is that the circle is not contractible to zero: At the
origin—which is inside the circle and at which ρ =0—B is not defined.
This vector field should look familiar. It is the magnetic field due to a long
straight wire carrying a current along the z-axis. According to Amp`ere’s circuital
law,thelineintegralofB along any closed curve encircling the wire, such as the
above circle, gives, up to a multiplicative constant, the current in the wire, and this
current is not zero.
Example 16.4.4. A vector field that can be written ascentral force fields
are conservative
F = f(r)r,
where r is the displacement vector from the origin, is conservative. It is instructive
to show this using both Cartesian and spherical coordinate systems.
First, in Cartesian coordinates
F = xf(r)
ˆ
e
x
+ yf(r)
ˆ
e
y
+ zf(r)
ˆ
e
z
and the curl is
∇ ×F =
ˆ
e
x
ˆ
e
y
ˆ
e
z
∂
∂x
∂
∂y
∂
∂z
xf yf zf
=
ˆ
e
x
(
∂
∂y
(zf) −
∂
∂z
(yf)
)
+
ˆ
e
y
(
∂
∂z
(xf) −
∂
∂x
(zf)
)
+
ˆ
e
z
(
∂
∂x
(yf) −
∂
∂y
(xf)
)
.
Concentrating on the x-component first and using the chain rule, we have
∂
∂y
(zf)=z
∂f
∂y
= z
df
dr
∂r
∂y
= zf
∂r
∂y
.
But
∂r
∂y
=
∂
∂y
x
2
+ y
2
+ z
2
=
y
r
.
Thus,
∂
∂y
(zf)=yzf
.
Similarly,
∂
∂z
(yf)=yzf
.
Therefore, the x-component of ∇×F is zero. The y-andz-components can also be
shown to be zero, and we get ∇ ×F =0.
On the other hand, using spherical coordinates, we easily obtain
∇ ×F =
1
r
2
sin θ
ˆ
e
r
ˆ
e
θ
r
ˆ
e
ϕ
r sin θ
∂
∂r
∂
∂θ
∂
∂ϕ
rf(r)0 0
=0.
Obviously, the use of spherical coordinates simplifies the calculation consi-
derably.

16.4 The Curl 435
The preceding example shows that
Box 16.4.1. Any well-behaved vector field whose magnitude is only a
function of radial distance, r, and whose direction is along r is conserva-
tive. Such vector fields are generally known as central vector fields.
16.4.1 The Laplacian
Combining divergence and the gradient gives the Laplacian. Using Equation
(16.4) in Theorem 16.3.1, we get
Laplacian in
curvilinear
coordinates
Theorem 16.4.5. The Laplacian of a function f is the divergence of gradient
of f and—in a curvilinear coordinate system—is given by
∇
2
f =
1
h
1
h
2
h
3
(
∂
∂q
1
h
2
h
3
h
1
∂f
∂q
1
+
∂
∂q
2
h
1
h
3
h
2
∂f
∂q
2
+
∂
∂q
3
h
1
h
2
h
3
∂f
∂q
3
)
.
For cylindrical coordinates the Laplacian is
∇
2
f =
1
ρ
∂
∂ρ
ρ
∂f
∂ρ
+
1
ρ
2
∂
2
f
∂ϕ
2
+
∂
2
f
∂z
2
(16.18)
and for spherical coordinates it is
∇
2
f =
1
r
2
∂
∂r
r
2
∂f
∂r
+
1
r
2
sin θ
(
∂
∂θ
sin θ
∂f
∂θ
+
1
sin θ
∂
2
f
∂ϕ
2
)
. (16.19)
Equations (16.7) and (16.19) allow us to write the angular momentum
differential operator derived in Example 15.3.1 in spherical coordinates, which
is the most common way of writing it. We note that
∂
∂r
r
2
∂f
∂r
=2r
∂f
∂r
+ r
2
∂
2
f
∂r
2
,
and
r ·(∇f)=r
∂f
∂r
,
and
(r · ∇)
2
f = r
∂
∂r
∂f
∂r
= r
∂f
∂r
+ r
2
∂
2
f
∂r
2
.
Substituting these plus (16.19) in (15.22) yields
L
2
f = −
1
sin θ
(
∂
∂θ
sin θ
∂f
∂θ
+
1
sin θ
∂
2
f
∂ϕ
2
)
. (16.20)
Therefore, the angular momentum operator depends only on angles in spher-
ical coordinates.

436 Curvilinear Vector Analysis
16.5 Problems
16.1. The divergence of a vector can be obtained in any coordinate system
by brute force calculation. In this problem you are asked to find ∇ · A in
cylindrical coordinates.
(a) Express A
x
in terms of cylindrical coordinates and components. Hint:
Write A in cylindrical ccordinates and take the dot product with
ˆ
e
x
expressing
everything in terms of cylindrical ccordinates.
(b) Use the chain rule
∂A
x
∂x
=
∂A
x
∂ρ
∂ρ
∂x
+
∂A
x
∂ϕ
∂ϕ
∂x
+
∂A
x
∂z
∂z
∂x
where A
x
is what you found in (a).
(c) Do the same with A
y
and A
z
, and add the three terms to obtain the
divergence in cylindrical coordinates.
16.2. Find the divergence of a vector in spherical coordinates following the
procedure outlined in Problem 16.1.
16.3. Find the gradient of a function in cylindrical and spherical coordinates
following a procedure similar to the one outlined in Problem 16.1.
16.4. Find the curl of a vector in cylindrical and spherical coordinates fol-
lowing a procedure similar to the one outlined in Problem 16.1.
16.5. Start with the Laplacian in Cartesian coordinates.
(a) By using the chain rule and expressing the second derivatives in cylindrical
coordinates, find the Laplacian in cylindrical coordinates.
(b) Do the same for spherical coordinates.
16.6. The elliptic cylindrical coordinates (u, θ, z)are given by
x = a cosh u cos θ
y = a sinh u sin θ
z = z
where a is a constant.
(a) What is the expression for the gradient of a function f in elliptic cylindri-
cal coordinates?
(b) What is the expression for the divergence of a vector A in elliptic cylin-
drical coordinates?
(c) What is the expression for the curl of a vector A in elliptic cylindrical
coordinates?
(d) What is the expression for the Laplacian of a function f in elliptic cylin-
drical coordinates?

16.5 Problems 437
16.7. The prolate spheroidal coordinates (u, θ, ϕ)aregivenby
x = a sinh u sin θ cos ϕ
y = a sinh u sin θ sin ϕ
z = a cosh u cos θ
where a is a constant.
(a) What is the expression for the gradient of a function f in prolate spheroidal
coordinates?
(b) What is the expression for the divergence of a vector A in prolate spheroidal
coordinates?
(c) What is the expression for the curl of a vector A in prolate spheroidal
coordinates?
(d) What is the expression for the Laplacian of a function f in prolate
spheroidal coordinates?
16.8. The toroidal coordinates (u, θ, ϕ)aregivenby
x =
a sinh u cos ϕ
cosh u − cos θ
y =
a sinh u sin ϕ
cosh θ −cos θ
z =
a sin u
cosh u − cos θ
(a) What is the expression for the gradient of a function f in toroidal coordi-
nates?
(b) What is the expression for the divergence of a vector A in toroidal coor-
dinates?
(c) What is the expression for the curl of a vector A in toroidal coordinates?
(d) What is the expression for the Laplacian of a function f in toroidal coor-
dinates?
16.9. The paraboloidal coordinates (u, v, ϕ)aregivenby
x =2auv cos ϕ
y =2auv sin ϕ
z = a(u
2
− v
2
)
where a is a constant.
(a) What is the expression for the gradient of a function f in paraboloidal
coordinates?
(b) What is the expression for the divergence of a vector A in paraboloidal
coordinates?
(c) What is the expression for the curl of a vector A in paraboloidal coordi-
nates?
(d) What is the expression for the Laplacian of a function f in paraboloidal
coordinates?
438 Curvilinear Vector Analysis
16.10. The three-dimensional bipolar coordinates (u, θ, ϕ)aregivenby
x =
a sin θ cos ϕ
cosh u − cos θ
y =
a sin θ sin ϕ
cosh u − cos θ
z =
a sinh u
cosh u − cos θ
(a) What is the expression for the gradient of a function f in three-dimensional
bipolar coordinates?
(b) What is the expression for the divergence of a vector A in three-dimensional
bipolar coordinates?
(c) What is the expression for the curl of a vector A in three-dimensional
bipolar coordinates?
(d) What is the expression for the Laplacian of a function f in three-dimensional
bipolar coordinates?

Chapter 17
Tensor Analysis
Our study of vectors in this part of the book has been limited to their anal-
ysis in specific coordinate systems, and although we touched on the general
curvilinear coordinate system, our treatment aimed at orthogonal coordinates,
and specifically at only three-dimensional spherical and cylindrical coordinate
systems. Many situations in physics demand a three-fold generalization: non-
orthogonal coordinate systems, higher-dimensional spaces, and objects, called
tensors, whose components have more subscripts than one. This chapter is
devoted to an analysis of tensors.
17.1 Vectors and Indices
Vector manipulations will be greatly simplified if equations are written in
terms of a general component. How do we accomplish this? Start with a
generic vector equation, which can be written as
U = V,
where U and V are, in general, vector expressions.Examplesofsuchan
equation are
B = ∇ ×A, E = −∇Φ, A =
#
b
a
f(r)
ˆ
e
r
dr.
You can also write each of these vector equations as three equations involving
components. Thus, the foregoing generic equation becomes
U
x
= V
x
,U
y
= V
y
,U
z
= V
z
.
It is very helpful to convert letter indices into number indices. Let x → 1,
y → 2, and z → 3, and write
1
U
1
= V
1
,U
2
= V
2
,U
3
= V
3
.
1
Note that the replacements here refer to indices not the Cartesian coordinates. The
latter will have somewhat different symbols in the sequel.

440 Tensor Anal ysi s
These equations are abbreviated as
U
i
= V
i
,i=1, 2, 3. (17.1)
This is what we mean by an equation in terms of a general component: The
index i refers to any one of the components of the vectors on either side of
the equation. It is called a free index because it is free to take any one of the
free index defined
values between 1 and 3. An important property of a free index is that
Box 17.1.1. A free index appears once and only once on both sides of
avectorequation.
One can use any symbol to represent a free index, although the most common
symbols used are i, j, k, l, m,andn. Thus, Equation (17.1) can be written in
any one of the following alternative ways:
U
j
= V
j
,j=1, 2, 3,
U
p
= V
p
,p=1, 2, 3,
U
♥
= V
♥
, ♥ =1, 2, 3.
Of special interest are the components of the position vector r.Theseare
denoted by x
i
rather than r
i
. Thus, the vector relation R = r −r
is writtenindexed Cartesian
coordinates
as
X
j
= x
j
− x
j
,j=1, 2, 3.
An abbreviation used for derivatives with respect to Cartesian coordinates
(which coincide with the components of the position vector) is given as follows.
First ∂/∂x is replaced by ∂/∂x
1
, and the latter by the much shorter notation,
∂
1
. Similarly, ∂/∂y becomes ∂
2
,and∂/∂z becomes ∂
3
. In particular, the
general component of the gradient of a function f will be written as ∂
k
f, k =
1, 2, 3.
components of
gradient
All operations on vectors can be translated into the language of indexed
relations. For example, A+B = C is equivalent to A
k
+B
k
= C
k
,k=1, 2, 3,
and A = αB becomes A
k
= αB
k
,k=1, 2, 3, etc. The two operations of
vector multiplication are a little more involved and we treat them separately
in the following.
First let us consider the dot product. In terms of components, the dot
product of A and B can be written as
A ·B = A
x
B
x
+ A
y
B
y
+ A
z
B
z
.
Converting to number indices, we get
A ·B = A
1
B
1
+ A
2
B
2
+ A
3
B
3
=
3
i=1
A
i
B
i
.

17.1 Vectors and Indices 441
We now introduce a further simplification in notation due to Einstein, which
gets rid of the clumsy summation sign:
Einstein
summation
convention
Box 17.1.2. (Einstein Summation Convention). Whenever an in-
dex is repeated, it is a dummy index and is summed from 1 to 3.
Using this convention we write the dot product as dot product
A · B = A
i
B
i
. (17.2)
No summation sign is needed as long as we remember that the repeated index
i is summed over. Since the repeated index is a dummy index, we can change
it to any other symbol. Thus,
A · B = A
k
B
k
= A
j
B
j
= A
n
B
n
= A
♥
B
♥
= ··· .
Example 17.1.1.
In this example, we write some of the familiar vector relations
in both vector form and component form:
E = −∇Φ ⇐⇒ E
k
= −∂
k
Φ,
∇ · A ⇐⇒ ∂
j
A
j
,
##
S
A · da =
##
V
#
∇ · A dV ⇐⇒
##
S
A
k
da
k
=
##
V
#
∂
j
A
j
dV,
∇
2
Φ ⇐⇒ ∂
m
∂
m
Φ,
∇ · (fA)=A ·∇f + f∇ ·A ⇐⇒ ∂
i
(fA
i
)=A
i
∂
i
f + f∂
i
A
i
.
The reader is urged to verify all these relations, remembering the Einstein summa-
tion convention.
17.1.1 Transformation Properties of Vectors
Section 6.2.1 discussed the transformation of vectors, i.e., the way the compo-
nents of a vector change when they are expressed in term of a new basis. To
coordinates with
superscripts
initiate the transformations relevant to the present chapter, let us begin with
the position vector r, which in one Cartesian coordinate system (with basis
{
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
}) is represented by (x
1
,x
2
,x
3
),andinanotherby(¯x
1
, ¯x
2
, ¯x
3
). Here
we are beginning to introduce new notation and terminology : instead of “vec-
tor space,” we use “Cartesian coordinate system,” and instead of subscripts,
we use superscripts to label the coodinates.
Since both (x
1
,x
2
,x
3
), and (¯x
1
, ¯x
2
, ¯x
3
) are components of the same posi-
tion vector, they are related via Equation (6.29):
¯x
1
= a
11
x
1
+ a
12
x
2
+ a
13
x
3
,
¯x
2
= a
21
x
1
+ a
22
x
2
+ a
23
x
3
, (17.3)
¯x
3
= a
31
x
1
+ a
32
x
2
+ a
33
x
3
.
