Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

15.3 Laplacian 411

15.3 Laplacian

The divergence of the gradient is an important and frequently occurring op-

erator called the Laplacian:

Laplacian of a

function

∇ · (∇f) ≡∇

f =

∂

∂x

∂

∂y

∂

∂z

. (15.13)

Laplacian occurs throughout physics, in situations ranging from the waves on

Laplacian is found

everywhere!

a drum to the diﬀusion of matter in space, the propagation of electromagnetic

waves, and even the most basic behavior of matter on a subatomic scale, as

governed by the Schr¨odinger equation of quantum mechanics.

We discuss one situation in which the Laplacian occurs naturally. The

result of the example above and Theorem 13.2.4 can be combined to obtain

an important equation in electrostatics and gravity called the Poisson equa-

tion: ∇ ·(−∇Φ) = 4πKρ

,or Poisson equation

∇

Φ(r)=−4πKρ

(r). (15.14)

This is a partial diﬀerential equation whose solution determines the potential

at various points in space.

In many situations the density in the region of

interest is zero. Then the RHS vanishes and we obtain an important special

case of the above equation called Laplace’s equation:

Laplace’s equation

∇

Φ(r)=0. (15.15)

Consider a ﬁxed point P in space with Cartesian coordinates (x

)

and position vector r

. Take another (variable) point with Cartesian coordi-

nates (x, y, z) and position vector r. By direct diﬀerentiation, one can verify

that

∇ ·



r − r

|r − r



at all points of space except at r = r

for which the vector is not deﬁned.

Moreover, if S is any closed surface bounding a volume V ,wehave



r −r

|r − r



· da ≡ Ω

4π if P is in V,

0ifP is not in V,

by Theorem 12.1.2. On the other hand, the divergence theorem relates the

LHS of this equation with the volume integral of divergence. Thus,

∇ ·



r −r

|r − r



dV =

4π if P is in V,

0ifP is not in V.

(15.16)

The reader should consider this, and any other diﬀerential equation, as a local equation,

meaning that the derivatives on the LHS and the quantities on the RHS are to be evaluated

at the same point.

412 Applied Vector Analysis

This shows that ∇·[(r −r

)/|r − r

] has the property that it is zero every-

where except at P , but whose volume integral is not zero. This is reminiscent

of the three-dimensional Dirac delta function. In fact, it follows from Equation

(15.16) that

∇ ·



r − r

|r − r



=4πδ(r − r

). (15.17)

Using Equation (15.2) and the deﬁnition of Laplacian, we also get

relation between

Laplacian and

Dirac delta

function

∇



|r − r



= −4πδ(r −r

). (15.18)

The last double-del operation we consider is

∇ × (∇× A)=∇(∇ ·A) −∇

A (15.19)

which holds only in Cartesian coordinates and can be veriﬁed component by

component.

Example 15.3.1.

Angular Momentum Operator In quantum mechanics,

the angular momentum L = r ×p becomes the diﬀerential operator L = −ir ×∇,

where  is the reduced Planck constant, which we set equal to 1 in the following

discussion. The quantity L

≡|L|

appears frequently in applications of quantum

mechanics. It is therefore instructive to compute this quantity.

Since L

is a diﬀerential operator, we let it act on some function f and carry

out the diﬀerentiation until we get a simple result. Since

= L

+ L

we let each component act on f separately. First note that

f = −i (r × ∇f)

= −i



∂f

∂z

− z

∂f

∂y



f = −i (r × ∇f)

= −i



∂f

∂x

− x

∂f

∂z



(15.20)

f = −i (r × ∇f)

= −i



∂f

∂y

− y

∂f

∂x



Therefore,

−L

f =



∂

∂z

− z

∂

∂y



∂f

∂z

− z

∂f

∂y



= y

∂

∂z

+ z

∂

∂y

− y

∂f

∂y

− z

∂f

∂z

− 2yz

∂

∂y∂z

. Similarly,

−L

f = x

∂

∂z

+ z

∂

∂x

− x

∂f

∂x

− z

∂f

∂z

− 2xz

∂

∂x∂z

and

−L

f = x

∂

∂y

+ y

∂

∂x

− x

∂f

∂x

− y

∂f

∂y

− 2xy

∂

∂x∂y

15.3 Laplacian 413

Adding the three components and using a little algebra, we get

−L

f = r

∇

f −



∂

∂x

+ y

∂

∂y

+ z

∂

∂z



− 2r · (∇f) − 2



∂

∂y∂z

+ xz

∂

∂x∂z

+ xy

∂

∂x∂y



. (15.21)

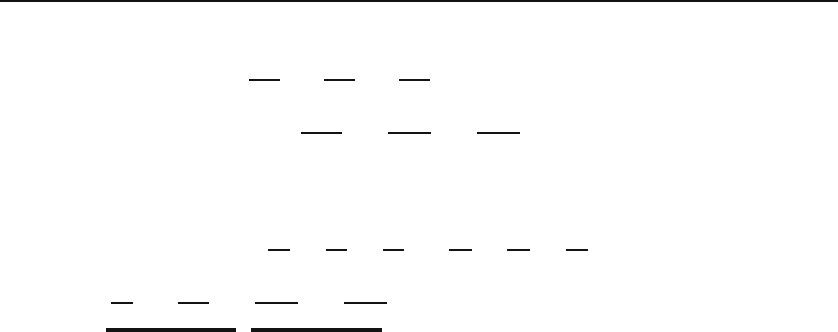
Let A denote the sum of the two expressions in the large parentheses. We can write

A in a compact form by expanding (r · ∇)(r · ∇f):

(r · ∇)

f ≡ (r · ∇)(r · ∇f)=



∂

∂x

+ y

∂

∂y

+ z

∂

∂z



∂f

∂x

+ y

∂f

∂y

+ z

∂f

∂z



= x

∂f

∂x

+ x

∂

∂x

+ xy

∂

∂x∂y

+ xz

∂

∂x∂z



 

comes from x diﬀerentiation

+terms from y and z diﬀerentiation.

Adding the terms from x, y,andz diﬀerentiations we obtain

(r · ∇)

f = r ·(∇f)+A or A =(r ·∇)

f − r · (∇f).

Substituting this in (15.21) yields

f = −r

∇

f + r · (∇f)+(r · ∇)

f. (15.22)

As a diﬀerential operator, L

is written as

= −r

∇

+ r · ∇ +(r ·∇)

. (15.23)

We shall come back to this discussion in Chapter 17 to show how index manipulation

eases the calculation (see Example 17.3.3).



15.3.1 A Primer of Fluid Dynamics

We have already talked about the ﬂow of a ﬂuid in Section 13.2.3, where

we derived the continuity equation, which states the conservation of mass in

mathematical terms. We now want to take up the dynamics of a ﬂuid, i.e.,

the motion of various parts of the ﬂuid due to the forces acting on them.

Consider a volume V of the ﬂuid bounded by a surface S. The pressure p

exerted from outside at any point of S in the element of area da is normal to

S at that point and pointing into the volume V . Thus, the element of force

due to pressure is −pda. If pressure is the only source of force on the volume

V of the ﬂuid, then the total force on V is

F = −

pda.

Using Equation (13.12), we rewrite this as

F = −

pda = −

∇pdV.

414 Applied Vector Analysis

This shows that ∇p is a force density, whose volume integral gives the force.

If the density of the ﬂuid is ρ and the mass element dm in V has velocity v,

then the “mass time acceleration” is dm dv/dt = ρdV (dv/dt), and the total

“mass time acceleration” is the volume integral of this quantity. If there are

other forces acting on the ﬂuid described by a force density f, we can add it

to the right-hand side. Thus, Newton’s second law of motion gives

ρ(dv/dt) dV = −

∇pdV +

f dV,

and this holds for any volume V , in particular for an inﬁnitesimal volume for

which the integrals become the integrand. Hence, the second law of motion

for the ﬂuid is

ρ(dv/dt)=−∇p + f. (15.24)

The total time derivative of velocity is

∂v

∂t

∂v

∂x

∂v

∂y

∂v

∂z

∂v

∂t

+(v · ∇)v.

Substituting this in (15.24) and dividing by ρ yields

Euler’s equation of

ﬂuid dynamics

∂v

∂t

+(v · ∇)v =

−∇p + f

. (15.25)

This is Euler’s equation and is one of the fundamental equations of ﬂuid

dynamics.

The force density f in Euler’s equation is usually that of the gravitational

force. Since the gravitational force on an element ρdV is gρdV,whereg is

the gravitational acceleration (or ﬁeld), the gravitational force density is ρg

and (15.25) becomes

∂v

∂t

+(v · ∇)v =

−∇p

+ g. (15.26)

Example 15.3.2.

In hydrostatic situations with a uniform gravitational ﬁeld the

ﬂuid is not moving and Equation (15.26) becomes

∇p = ρg,

and if g is in the negative z-direction, then

∂p

∂x

∂p

∂y

=0,

∂p

∂z

= −ρg.

Thus the pressure is independent of x and y, and depends only on height z.We

assume that the ﬂuid (really the liquid) is incompressible, meaning that its density

does not depend on the pressure. Then, integrating the z equation gives

p = −ρgz + C.

If the liquid has a free surface at z = h where the pressure is p

,thenC = p

+ ρgh,

and

p = p

+ ρg(h − z).



15.4 Maxwell’s Equations 415

Example 15.3.3. Stellar equilibrium Astarisalargemassofﬂuidheld

together by gravitational attraction. If the star is in equilibrium, its ﬂuid has no

motion and (15.26) becomes

∇p = ρg or ∇p = −ρ∇Φ

where Φ is the gravitational potential. Dividing this equation by ρ, and taking the

divergence of both sides, we obtain

∇ ·



∇p



= −∇

Φor∇ ·



∇p



=4πGρ

where we used the Poisson equation (15.14). For a spherically symmetric star, only equation for stellar

equilibriumthe radial coordinate enters in the equation above, and borrowing from the next

chapter the expressions (16.7) for gradient and (16.12) for divergence in spherical

coordinates, the equation above takes the form





=4πGρ

This is one of the fundamental equations of astrophysics.



15.4 Maxwell’s Equations

No treatment of vector analysis is complete without a discussion of Maxwell’s

equations. Electromagnetism was both the producer and the consumer of

vector analysis. It started with the accidental discovery by

Orsted in 1820

that an electric current produced a magnetic ﬁeld. Subsequently, an intense

search was undertaken by many physicists such as Amp`ere and Faraday to

ﬁnd a connection between electric and magnetic phenomena. By the mid-

1800s, a fairly good theory of electromagnetism was attained which, in the

contemporary language of vectors is translated in the following four equations:

the four equations

that Maxwell

inherited in

integral form

(1)

E · da =



;(2)

B · da =0;

(3)

E · dr = −

dφ

;(4)

B · dr = μ

I. (15.27)

The ﬁrst integral, Gauss’s law (or Coulomb’s law in disguise), states that the

electric ﬂux through the closed surface S is essentially the total charge Q in

the volume surrounded by S. The second integral says that the correspond-

ing ﬂux for a magnetic ﬁeld is zero. The fact that this holds for an arbitrary

surface implies that there are no magnetic charges. The third equation, Fara-

day’s law, connects the electric ﬁeld to the rate of change of magnetic ﬂux

. Finally, the last equation, Amp`ere’s law, states that the source of the

magnetic ﬁeld is the electric current I. The constant 

and μ

arise from a

particular set of units used for charges and currents.

416 Applied Vector Analysis

15.4.1 Maxwell’s Contribution

Equations (15.27) can be cast in diﬀerential form as well. The diﬀerential

form of the equations is important because it places particular emphasis on

the ﬁelds which are the primary objects. The diﬀerential form of the equations

above are:

the four equations

that Maxwell

inherited in

diﬀerential form

(1) ∇ ·E =



;(2)∇ · B =0;

(3) ∇ ×E = −

∂B

∂t

;(4)∇ × B = μ

J. (15.28)

We have already derived the ﬁrst two equations in Theorem 13.2.4 and Equa-

tion (15.9). Here we derive the third equation and leave the derivation of

the last equation—which is very similar to that of the third—to the reader.

Stokes’ theorem turns the LHS of the third equation of (15.27) into

LHS =

∇ × E · da.

The RHS is

−

dφ

= −

B · da =



−

∂B

∂t



·da,

where we have assumed that the change in the ﬂux comes about solely due

to a change in the magnetic ﬁeld. This makes it possible to push the time

diﬀerentiation inside the integral, upon which it becomes a partial derivative

because B is a function of position as well. Since the last two equations hold

for arbitrary S, the integrands must be equal. This proves the third equation

in (15.28).

Maxwell inherited the four equations in (15.28), and started pondering

about them in the 1860s. He noticed that while the second and third are

Maxwell discovers

the inconsistency

of Equation

(15.28) with the

conservation of

electric charge,

and modiﬁes the

last equation to

resolve the

inconsistency.

consistent with other aspects of electromagnetism, the other two equations

lead to a contradiction. Let us retrace his argument. By Equation (15.5),

the divergence of the LHS of the last equation of (15.28) vanishes. Therefore,

taking the divergence of both sides, we get ∇ · J = 0. This contradicts the

diﬀerential form of the continuity equation (13.22) for charges which expresses

the conservation of electric charge. Because of the ﬁrm establishment of the

charge conservation, Maxwell decided to try altering the four equations to

make them compatible with charge conservation. The clue is in the ﬁrst

equation. If we diﬀerentiate that equation with respect to time, we obtain

∂

∂t

∇ · E =



∂ρ

∂t

⇒ ∇ ·



∂E

∂t





∂ρ

∂t

⇒ ∇ ·





∂E

∂t



∂ρ

∂t

This suggested to Maxwell that, if the four equations are to be consistent

with charge conservation, the fourth equation had to be modiﬁed to include



∂E/∂t. With this modiﬁcation, the four equations in (15.28) becomethe four Maxwell

equations

15.4 Maxwell’s Equations 417

(1) ∇ ·E =



;(2)∇ · B =0;

(3) ∇ ×E = −

∂B

∂t

;(4)∇ × B = μ

J + μ



∂E

∂t

. (15.29)

It was a great moment in the history of physics and mathematics when

Maxwell, prompted solely by the forces of logic and pure deduction, intro-

duced the second term in the last equation. Such moments were rare prior

mathematics and

the force of logic

and human

reasoning unravel

one of the greatest

secrets of Nature!

to Maxwell, and with the exception of Copernicus’s introduction of the he-

liocentric theory of the solar system and Descartes’s introduction of analytic

geometry, deductive reasoning was the exception rather than the rule. The-

ories and laws were empirical (or inductive); they were introduced to ﬁt the

data and summarize, more or less directly, the numerous observations made.

Maxwell broke this tradition and set the stage for deductive reasoning which,

after a great deal of struggle to abandon the inductive tradition, became the

norm for modern physics.

Today, we aptly call all four equations in (15.29) Maxwell’s equations,

although his contribution to those equations was a “mere” introduction of

the second term on the RHS of the last equation. However, no other “small”

contribution has ever aﬀected humankind so enormously. This very “small”

contribution was responsible for Maxwell’s prediction of the electromagnetic

waves which were subsequently produced in the laboratory in 1887—only eight

years after Maxwell’s premature death—and put to technological use in 1901

in the form of the ﬁrst radio. Today, Maxwell’s equations are at the heart of

every electronic device. Without them, our entire civilization, as we know it,

would be nonexistent.

15.4.2 Electromagnetic Waves in Empty Space

Let us look at some of the implications of Maxwell equations. Taking the curl from Maxwell’s

equations to wave

equation

of the third Maxwell’s equation and using (15.19) and the ﬁrst and fourth

equations of (15.29), we obtain for the LHS

LHS = ∇ ×(∇ ×E)=∇(∇ ·E) −∇

E =



∇ρ −∇

and for the RHS

RHS = − ∇ ×



∂B

∂t



= −

∂

∂t

(∇× B)=−

∂

∂t



J + μ



∂E

∂t



In particular, in free space, where ρ =0=J, these equations give

∇

E − μ



∂

∂t

=0. (15.30)

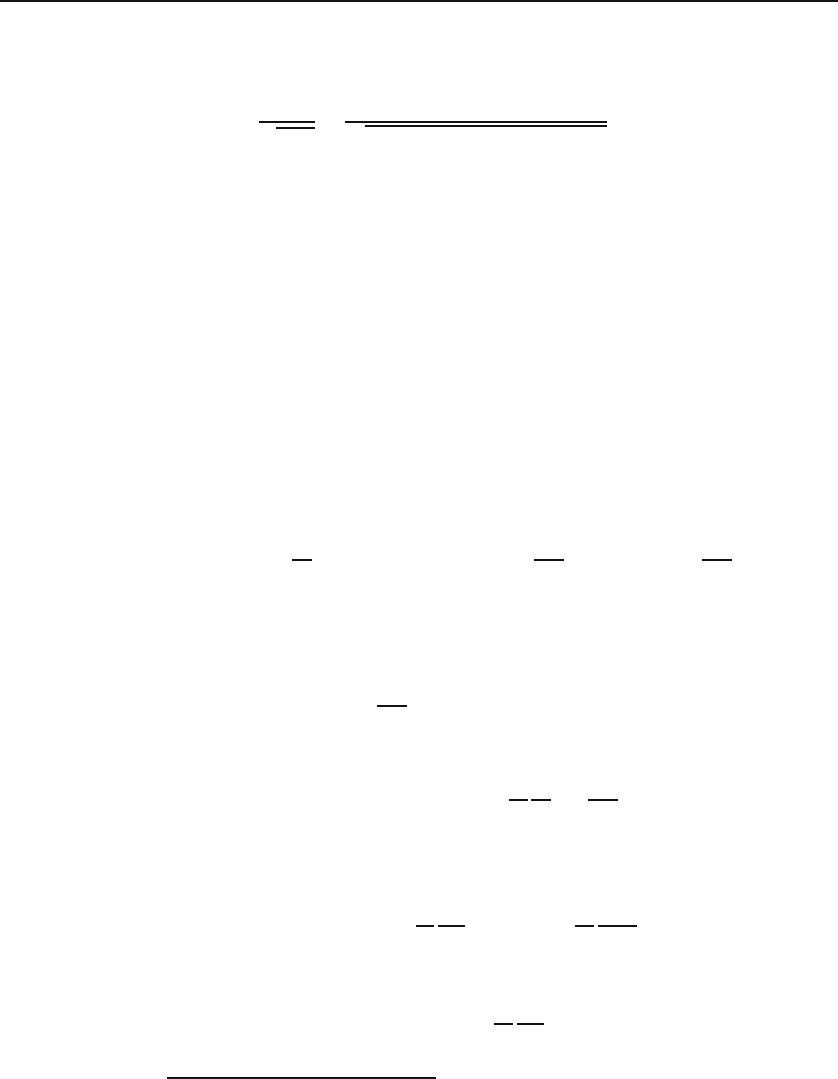
418 Applied Vector Analysis

This is a three-dimensional wave equation.

Recall that the inverse of the co-

eﬃcient of the second time derivative is the square of the speed of propagation

of the wave. It follows that

v =

√





(4π × 10

−7

)(8.854 × 10

−12

)

=2.998 × 10

m/s,

i.e., that the electric ﬁeld propagates in empty space with the speed of light,

c. The reader may check that the magnetic ﬁeld also satisﬁes the same wave

equation, and that it too propagates with the same speed. In fact, it can be

shown that the so-called plane wave solutions of Maxwell’s equations consist

of an electric and a magnetic component which are coupled to one another

electromagnetic

waves propagate

at the speed of

light.

and, therefore do not propagate independently (see Problem 15.9).

Sometimes it is more convenient to work with potentials than the ﬁelds

themselves. The vanishing of the divergence of magnetic ﬁelds suggests that

B = ∇ × A where A is the vector potential [see also Equation (15.6)]. The

vector potential, as its scalar counterpart, has some degree of arbitrariness,

because adding the gradient of an arbitrary function does not change its curl.

This is an example of gauge transformation whereby a measurable physical

gauge

transformation

quantity—the magnetic ﬁeld, here—does not change when another (nonmea-

surable) physical quantity is changed. Using this expression for B in the third

Maxwell equation, we obtain

∇ × E = −

∂

∂t

(∇× A) ⇒ ∇ ×



E +

∂A

∂t



=0 ⇒ E +

∂A

∂t

= −∇Φ,

where we switched the order of diﬀerentiation with respect to position and

time, and used the fact that if the curl of a vector vanishes, that vector is the

gradient of a function (Box 15.1.1). We therefore write

E = −

∂A

∂t

− ∇ΦandB = ∇× A. (15.31)

Substituting these two expressions in the fourth Maxwell equation, we obtain

∇ × (∇× A)=μ

J +

∂

∂t



−

∂A

∂t

− ∇Φ



Expanding the LHS using the double curl identity of Equation (15.19), and

switching time and space partial derivatives yields

∇



∇ · A +

∂Φ

∂t



−∇

A +

∂

∂t

= μ

Because of the gauge freedom, we can choose A and Φ to satisfy

∇ · A +

∂Φ

∂t

=0. (15.32)

The reader may be familiar with the one-dimensional wave equation in which only one

second partial derivative with respect to a single space coordinate appears.

15.4 Maxwell’s Equations 419

This choice is called the Lorentz gauge, from which it follows that Lorentz gauge

∇

A −

∂

∂t

= −μ

J. (15.33)

Similarly, by taking the divergence of the ﬁrst equation in (15.31) and using

the ﬁrst Maxwell equation and the Lorentz gauge, we obtain

∇

Φ −

∂

∂t

= −



. (15.34)

Equations (15.32), (15.33), and (15.34) are the fundamental equations of elec-

tromagnetic theory. They not only give the solutions in empty space, where

ρ = J = 0, but also when the sources are not zero, i.e., when the mechanism

of wave production becomes of interest, as in radiation and antenna theory.

Historical Notes

James Clerk Maxwell attended Edinburgh Academy where he had the nickname

“Dafty.” While still at school he had two papers published by the Royal Society of

Edinburgh. Maxwell then went to Peterhouse, Cambridge, but moved to Trinity,

where it was easier to obtain a fellowship. Maxwell graduated with a degree in

mathematics from Trinity College in 1854.

He held chairs at Marischal College in Aberdeen (1856) and married the daughter

of the Principal. However in 1860 Marischal College and King’s College combined

and Maxwell, as the junior of the department, had to seek another post. After failing

to gain an appointment to a vacant chair at Edinburgh he was appointed to King’s

College in London (1860) and became the ﬁrst Cavendish Professor of Physics at

Cambridge in 1871.

James Clerk

Maxwell 1831–1879

Maxwell’s ﬁrst major contribution to science was a study of the planet Sat-

urn’s rings, and won him the Adams Prize at Cambridge. He showed that stability

could be achieved only if the rings consisted of numerous small solid particles, an

explanation now conﬁrmed by the Voyager spacecraft.

Maxwell next considered the kinetic theory of gases. By treating gases statis-

tically in 1866 he formulated, independently of Ludwig Boltzmann, the Maxwell–

Boltzmann kinetic theory of gases. This theory showed that temperatures and heat

involved only molecular movement.

This theory meant a change from a concept of certainty, heat viewed as ﬂowing

from hot to cold, to one of statistics, molecules at high temperature have only a

high probability of moving toward those at low temperature. Maxwell’s approach

did not reject the earlier studies of thermodynamics but used a better theory of the

basis to explain the observations and experiments.

Maxwell’s most important achievement was his extension and mathematical for-

mulation of Michael Faraday’s theories of electricity and magnetic lines of force. His

paper On Faraday’s lines of force was read to the Cambridge Philosophical Society

in two parts, 1855 and 1856. Maxwell showed that a few relatively simple math-

ematical equations could express the behavior of electric and magnetic ﬁelds and

their interrelation.

The four partial diﬀerential equations, now known as Maxwell’s equations,

ﬁrst appeared in fully developed form in Treatise on Electricity and Magnetism

(1873). They are one of the great achievements of nineteenth-century mathematical

420 Applied Vector Analysis

physics. Solving these equations Maxwell predicted the existence of electromagnetic

waves and the fact that these waves propagate at the speed of light (1862). He

proposed that the phenomenon of light is therefore an electromagnetic phenomenon.

Maxwell left King’s College, London, in the spring of 1865 and returned to

his Scottish estate. He made periodic trips to Cambridge and, rather reluctantly,

accepted an oﬀer from Cambridge to be the ﬁrst Cavendish Professor of Physics in

1871. He designed the Cavendish laboratory and helped set it up.

15.5 Problems

15.1. Show that the curl of the gradient of a function is always zero.

15.2. Show that the divergence of the curl of a vector is always zero.

15.3. Verify Equation (15.19) component by component.

15.4. Provide the details of Example 15.3.1:

(a) Compute the three components of L and verify Equation (15.20).

(b) Calculate L

f, L

f and show that you obtain the expressions given

in the example.

f is as given in Equation (15.21).

(d) Show that A =(r ·∇)

f −r ·(∇f) and obtain (15.22). Here A is deﬁned

by the sum of the expressions in the two pairs of parentheses in Equation

(15.21)

15.5. By taking each component of dr



separately in a convenient coordinate

system show that its integral round any closed loop vanishes.

15.6. Recall that the total magnetic force on a current loop is given by

total magnetic

force on a current

loop in a constant

magnetic ﬁeld is

zero.

F = I

dr × B.

Show that the total force on a current loop located in a homogeneous magnetic

ﬁeld is zero.

15.7. Derive the diﬀerential form of Maxwell’s last equation from the corre-

sponding integral form.

15.8. Starting with Maxwell’s equations, show that the magnetic ﬁeld satis-

ﬁes the same wave equation as the electric ﬁeld. In particular, that it, too,

propagates with the same speed.

15.9. Consider E = E

i(ωt−k·r)

and B = B

i(ωt−k·r)

,wherei =

√

−1, E

, k,andω are constants. The E and the B so deﬁned represent plane waves

moving in the direction of the vector k.

(a) Show that they satisfy Maxwell’s equations in free space if:

(1) k ·E

=0; (2)k ·B

=0;

(3) k ×E

= ωB

;(4)k ×B

= −