Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

472 Tensor Anal ysi s

17.3. Verify Equation (17.23).

17.4. Let the scalar function φ be given by φ(x, y, z)=x

+ y

+ z and

x =sin¯x +cos¯y +¯z, y =¯x¯y +¯z, z =¯x

What is the functional form of

φ?

17.5. Show that the sum of two tensors of type (r, s) is a tensor of the same

type.

17.6. Derive Equation (17.29). Show that δ

12···n

=1.

17.7. Show that the inverse of a metric tensor given by

(x) ≡



p=1

∂x

p

∂x

p

is a tensor of type (2, 0). Here {x

i

} are as deﬁned in the beginning of Section

17.3.

17.8. Following Example 17.3.1, ﬁnd the metric tensor for cylindrical coordi-

nates.

17.9. Show that the dot products of Equations (17.36) and (17.37) do not

change in a general coordinate transformation.

17.10. Verify Equation (17.40) component by component.

17.11. Using indices, show that the divergence of a curl and the curl of a

gradient are both zero.

17.12. Using indices, prove the following “derivative” identities:

∇ ·(fA)=(∇f) ·A + f∇ ·A,

∇ × (fA)=(∇f) ×A + f∇× A,

∇(fg)=g∇f + f ∇g.

17.13. Using indices, prove the Green’s identity:

∇ · (g∇f − f ∇g)=g∇

f − f ∇

17.14. Prove the following vector identities using index notation for vectors:

∇ · (A ×B)=B ·∇ ×A −A ·∇× B,

∇ × (∇ ×A)=∇(∇ ·A) −∇

17.15. Show that the diﬀerence between any two aﬃne connections is a tensor

of type (1, 2).

17.6 Problems 473

17.16. Verify that Equation (17.46) combines the second and third Maxwell’s

equations.

17.17. Verify that F

αβ

= ∂

− ∂

satisﬁes Equation (17.46).

17.18. Diﬀerentiate both sides of Equation (17.45) with respect to x

and

raise the index β to be able to sum over it; use the symmetry of second

derivative and the antisymmetry of F

αβ

to show that the left-hand side is

zero. On the right-hand side, you should have something like μ

βσ

∂

Show that η

βσ

∂

= 0 expresses charge conservation or continuity equation

of Box 13.2.4.

17.19. With c =1andμ

=1/

, show that η

αν

∂

= 0 is the Lorentz

gauge condition [Equation (15.32)]

∂Φ

∂t

+ ∇ · A =0,

and that η

αν

∂

= μ

combines the two wave equations [Equations

(15.33) and (15.34)]

∂

∂t

−∇

A = μ

∂

∂t

−∇

Φ=μ

ρ.

17.20. Show that DA

of Box 17.4.1 is a covariant vector.

17.21. Show that

∂A

∂x

+Γ

is a tensor of type (1, 1).

17.22. Show that Γ

given in Equation (17.59) is an aﬃne connection, i.e.,

that it transforms according to Equation (17.52).

17.23. Show that the metric connection satisﬁes Equation (17.61).

17.24. (a) Find all the components of the aﬃne metric connection on the

surface of the sphere of Example 17.4.2.

(b) Derive Equation (17.62) from Equation (17.58).

(d) Show that cot θ = A cos ϕ + B sin ϕ is a solution of (17.65).

17.25. Show that the Riemann curvature tensor of Equation (17.68) is a

tensor of type (1, 3).

17.26. Example 17.5.1 showed that the Riemannian curvature tensor of the

Euclidean space, when expressed in Cartesian coordinates is zero. Since Rie-

mannian curvature tensor is a tensor it should be zero when expressed in

474 Tensor Anal ysi s

any coordinate system. Starting with the spherical components of the Eu-

clidean metric obtained in Example 17.3.1, ﬁnd the components of the metric

connection in spherical coordinates. From these calculate the components of

Riemannian curvature tensor and show that they all vanish.

17.27. Derive the expression for the Ricci curvature tensor of Example 17.5.2

and show that

θϕ

=0=R

ϕθ

θθ

=1,R

ϕϕ

=sin

θ.

Part V

Complex Analysis

Chapter 18

Complex Arithmetic

Complex numbers were developed because there was a need to expand the

notion of numbers to include solutions of algebraic equations whose proto-

type is x

+ 1 = 0. Such developments are not atypical in the history of

mathematics. The invention of irrational numbers occurred because of a need

for a number that could solve an equation of the form x

− 2 = 0. Similarly,

rational numbers were the oﬀspring of the operations of multiplication and

division and the quest for a number that gives, for example, 4 when multiplied

by 3, or, equivalently, a number that solves the equation 3x −4=0.

There is a crucial diﬀerence between complex numbers and all the num-

bers mentioned above: All rational, irrational, and, in general, real numbers

correspond to measurable physical quantities. However, there is no single

measurable physical quantity that can be described by a complex number.

A natural question then is this: What need is there for complex numbers

if no physical quantity can be measured in terms of them? The answer is that

although no single physical quantity can be expressed in terms of complex

numbers, apairof physical quantities can be neatly described by a single

complex number. For example, a wave with a given amplitude and phase can

be concisely described by a complex number. Another, more fundamental,

reason is that equations that describe the behavior of subatomic particles are

inherently complex.

18.1 Cartesian Form of Complex Numbers

We demand a number system broad enough to include solutions to the

equation

+1=0 or x

= −1.

Clearly the solution(s) cannot be real because a real number raised to the

second power gives a positive real number, and we want x

to be negative.

478 Complex Arithmetic

So we broaden the concept of numbers by considering complex numbers.

Such numbers are of the form

Cartesian form of

a complex number

z = x + iy with i ≡

√

−1andi

= −1. (18.1)

It turns out that we don’t need to introduce any other numbers to solve all

algebraic equations—equations of the form p(x)=0withp(x)apolynomial.

In fact, the fundamental theorem of algebra, to which we shall return,

states that all roots of any algebraic equation

+ a

n1−

n−1

+ ···+ a

x + a

with arbitrary real or complex coeﬃcients a

,...,a

,areinthecomplex

number system. In this sense, then, the complex number system is the most

complete system.

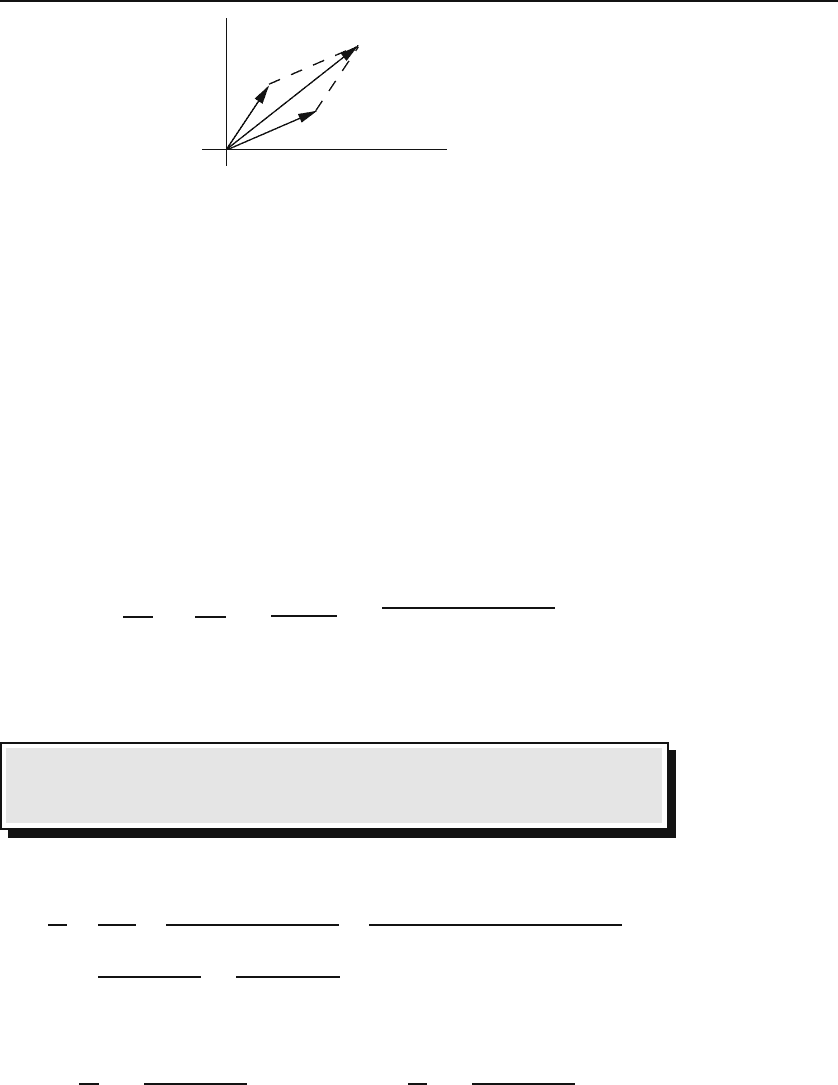
A complex number can be conveniently represented as a point (or equiv-

alently, as a vector) in the xy-plane, called the complex plane,asshown

complex plane,

real and imaginary

parts

in Figure 18.1. In Equation (18.1), x is called the real part of z, written

Re(z), and y is called the imaginary part of z, written Im(z). Similarly, the

horizontal axis in Figure 18.1 is named the real axis, and the vertical axis is

named the imaginary axis. The set of all complex numbers—or the set of

points in the complex plane—is denoted by C.

We can deﬁne various operations on C that are extensions of similar oper-

ations on the real number system, R. The only proviso is that i

= −1, and

that the ﬁnal form of an equation must be written as Equation (18.1)—with

real and imaginary parts. For instance, the sum of two complex numbers,

= x

+ iy

and z

= x

+ iy

,is

+ z

=(x

+ x

)+i(y

+ y

This sum can be represented in the complex plane as the vector sum of z

and

, as shown in Figure 18.2. The product of z

and z

can also be obtained:

=(x

+ iy

)(x

+ iy

)=x

+ x

(iy

)+iy

+ iy

(iy

)

= x

+ i(x

+ y

) −y

= x

− y

+ i(x

+ y

Thus,

Re(z

)=x

− y

Im(z

)=x

+ x

. (18.2)

Figure 18.1: Complex numbers as points or vectors in a plane.

18.1 Cartesian Form of Complex Numbers 479

+ z

Figure 18.2: Addition of complex numbers as addition of vectors.

To obtain this equation, we have implicitly used the fact that two complex

numbers are equal if and only if their real parts are equal and their imaginary

parts are equal.

The factor i in z allows new operations for complex numbers that do not

exist for real numbers. One such operation is complex conjugation.The

complex

conjugation

complex conjugate, z

∗

or ¯z,ofz is deﬁned as

∗

≡ ¯z =(x + iy)

∗

= x − iy (18.3)

which is obtained from z by replacing i with −i. We note immediately that

∗

=(x + iy)(x − iy)=x

+ y

= z

∗

which is a positive real number. The positive square root of zz

∗

is called the

absolute value of z and denoted by |z|. It is simply the length of the vector

absolute value

representing z in the xy-plane. Thus, we have

|z| =

√

∗

√

∗

z =



+ y



(Re(z))

+(Im(z))

. (18.4)

We can also deﬁne the division of two complex numbers using complex

conjugation.

Box 18.1.1. To ﬁnd the real and imaginary parts of a quotient, multiply

the numerator and denominator by the complex conjugate of the denomi-

nator.

So, for the ratio of z

,weget

∗

+ iy

)(x

− iy

)

+ y

+ i(y

− x

)

+ y

+ i

− x

Thus,





+ y

and Im





− x

+ y

. (18.5)

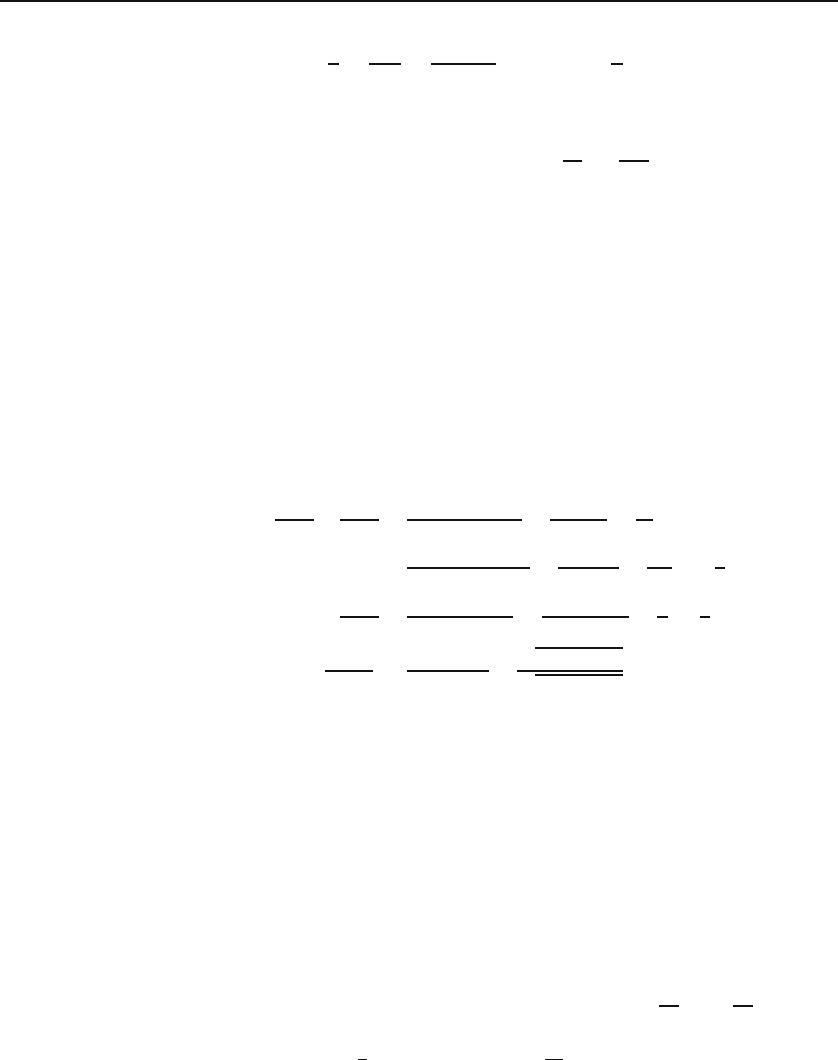
480 Complex Arithmetic

In particular,

∗

|z|

x − iy

+ y

and

= −i.

Some useful properties of absolute values are as follows:

properties of

absolute value of

complex numbers

| = |z

||z



|−|z



≤|z

+ z

|≤|z

|+ |z

|. (18.6)

This last inequality is called the triangle inequality and it comes directly

from the vector property of complex numbers. The right half of it can be

generalized to more than two complex numbers:





k=1



≤



k=1

|. (18.7)

Example 18.1.1.

Here we present some sample manipulations with complex num-

bers:

(1 + i)

=(1)

+(i)

+2i =1− 1+2i =2i,

1 − i

−

1+i

1+i − (1 − i)

(1 − i)(1 + i)

|1+i|

= i,

(1 + i)

−4

(1 + i)

(2i)(2i)

−4

= −

2+i

3 − i

(2 + i)(3 + i)

|3 − i|

5+i5

+(−1)

+ i



2i − 1

i − 2



|−1+i2|

|−2+i|



(−1)



(−2)

=1.

The equation |z − a| = b,wherea is a ﬁxed complex number and b is real and

positive, describes a circle of radius b with center at a ≡ a

+ ia

. This is easily

seen because

= |z − a|

= |(x + iy) −(a

+ ia

= |(x − a

)+i(y − a

=(x − a

)

+(y − a

)

We note that |z − a| is the distance between the two complex numbers z and a.

Therefore, |z − a| = b—with a a constant and z a variable—is the collection of all

points z that are at a distance b from a.



Complex conjugation satisﬁes some nice properties that we list below:properties of

complex

conjugation of

complex numbers

+ z

)

∗

= z

∗

+ z

∗

, (z

)

∗

= z

∗





∗

Re(z)=

(z + z

∗

), Im(z)=

(z − z

∗

), (18.8)

∗

)

∗

= z, (z

)

∗

=(z

∗

)

18.1 Cartesian Form of Complex Numbers 481

The complex conjugate of a function of z is easily obtained by substituting to ﬁnd the

complex conjugate

of a function,

change all its i’s

to −i.

∗

for z in that function.

This can be summarized as

(f(z))

∗

= f (z

∗

) (18.9)

which is equivalent to replacing every i with −i in the expression for f(z).

Historical Notes

In the ﬁrst half of the sixteenth century there was hardly any change from the

attitude or spirit of Arabs, whose work had put practical arithmetical calculations

in the forefront of mathematics, but merely an increase in the kind of activity

Europeans had learned from Arabs. Moreover, the technological advances spurred by

the Renaissance demanded further reﬁnement in magnitudes such as trigonometric

tables and astronomical observations.

By 1500 or so, zero was accepted as a number and irrational numbers were used

more freely in calculations. However, the problem of whether irrationals were really

numbers still troubled people. Michael Stifel (1486?–1567), the German mathemati-

cian, argued that

Since, in proving geometrical ﬁgures, when rational numbers fail us irrational

numbers . . . prove exactly those things which rational numbers could not prove

. . . we are compelled to assert that they truly are numbers . . . . On the other

hand, . . . that cannot be called a true number which is of such a nature that

it lacks precision [decimal representation].

He then argues that only whole numbers or fractions can be called true numbers, and

since irrationals are neither, they are not real numbers. Even a century later, Pascal,

Barrow,andNewton thought of irrational numbers as being understood in terms of

geometric magnitude; they were mere symbols that had no existence independent

of continuous geometrical magnitude.

Negative numbers were treated with equal suspicion by the sixteenth- and

seventeenth-century mathematicians. They were considered “absurd.” Jerome

Cardan (1501–1576), the great Italian mathematician of the Renaissance, was will-

ing to accept the negative numbers as roots of equations, but considered them as

“ﬁctitious,” while he called the positive roots real. Fran¸cois Vieta (1540–1603), a

lawyer by profession but recognized far more as the foremost mathematician of the

sixteenth century, discarded negative numbers entirely. Descartes accepted them in

part, but called negative roots of equations false, on the grounds that they repre-

sented numbers less than nothing.

An interesting argument against negative numbers was given by Antoine Arnauld

(1612–1694), a theologian and mathematician who was a close friend of Pascal.

Arnauld questioned the equality −1:1=1:(−1) because, he said, −1islessthan

+1;hence,Howcouldasmallernumberbetoagreaterasagreateristoasmaller?

Without having fully overcome their diﬃculties with irrational and negative

numbers, the Europeans were hit by another problem: the complex numbers !They

obtained these new numbers by extending the arithmetic operation of square root

This statement is not strictly true for all functions. However, only a mild restriction

is to be imposed on them for the statement to be true. We shall not go into details of

such restrictions because they require certain complex analytic tools which go beyond the

scope of this book. See Hassani, S. Mathematical Physics: A Modern Introduction to Its

Foundations, Springer-Verlag, 1999, Chapter 11 for details.

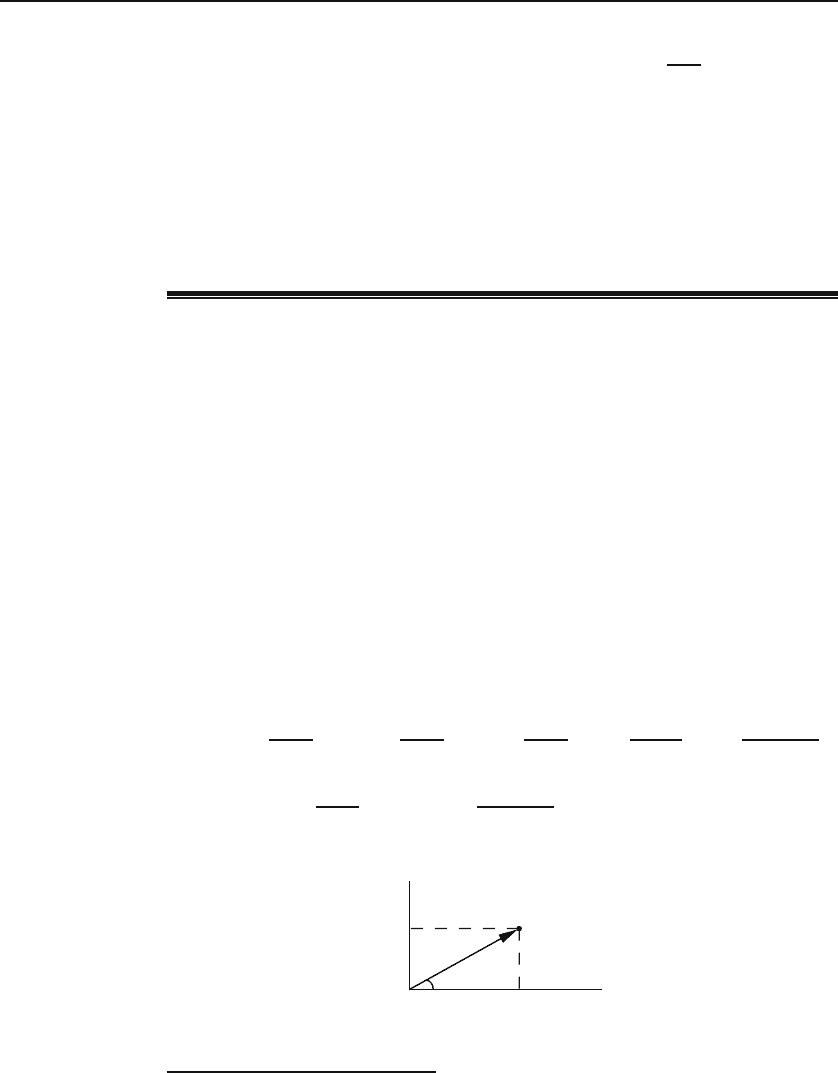
482 Complex Arithmetic

to whatever numbers appeared in solving quadratic equations. Thus Cardan sets

up and solves the problem of dividing 10 into two parts whose product is 40. The

equation is x(10−x) = 40, for which he obtains the roots 5±

√

−15 and then he says

“Putting aside the mental torture involved,” multiply these two roots and note that

the product is 25 − (− 15) or 40. He then states, “So progresses arithmetic subtlety

theendofwhich,asissaid,isasreﬁnedasitisuseless.”

Descartes also rejected complex roots and coined them “imaginary.” Even New-

ton did not regard complex roots as signiﬁcant, most likely because in his day they

lacked physical meaning. The confusion surrounding complex numbers is illustrated

by the oft-quoted statement by Leibniz, “The Divine Spirit found a sublime outlet

in that wonder of analysis, that portent of the ideal world, that amphibian between

being and not being, which we call the imaginary root of negative unity.”

18.2 Polar Form of Complex Numbers

The introduction of polar coordinates in the complex plane makes available

a powerful tool with which to facilitate complex manipulations. Figure 18.3

shows a complex number and its polar coordinates. In terms of these polar

coordinates, z can be written as

polar

representation of a

complex number

z = x + iy = r cos θ + ir sin θ = r(cos θ + i sin θ). (18.10)

Assuming that series of complex numbers can be manipulated as those of real

numbers,

we obtain the useful relation between imaginary exponentials and

trigonometric functions.

In Chapter 10 we presented the Maclaurin series for the exponential and

trigonometric functions. Let us assume that those functions are valid for

complex numbers as well. Then, we have

averyimportant

relation

iθ

∞



n=0

(iθ)

∞



n=even

(iθ)

∞



n=odd

(iθ)

∞



k=0

(iθ)

(2k)!

∞



k=0

(iθ)

2k+1

(2k +1)!

∞



k=0

(−1)

(2k)!

+ i

∞



k=0

(−1)

2k+1

(2k +1)!

=cosθ + i sin θ (18.11)

r sin θ

r cos θ

= |

Figure 18.3: Complex numbers in polar coordinates.

This assumption turns out to be correct. In particular, the power series expansion used

in the following example plays a central role in complex analysis.