Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

18.5 Problems 493
18.5 Problems
18.1. Find the real and imaginary parts of the following complex numbers:
(a) (2 −i)(3 + 2i). (b) (2 −3i)(1 + i). (c) (a − ib)(2a +2ib).
(d)
i
1+i
. (e)
1+i
2 − i
. (f)
1+3i
1 − 2i
.
(g)
1+2i
2 − 3i
. (h)
2
1 − 3i
. (i)
1 − i
1+i
.
(j)
5
(1 −i)(2 −i)(3 −i)
. (k)
1+2i
3 − 4i
+
2 − i
5i
.
18.2. Convert the following complex numbers to polar form and find all cube
roots of each:
(a) 2 − i. (b) 2 − 3i. (c) 3 − 2i. (d) i.
(e) − i. (f)
i
1+i
. (g)
1+i
2 − i
. (h)
1+3i
1 − 2i
.
(i) 1 + i
√
3. (j)
2+3i
3 − 4i
. (k) 27i. (l) − 64.
(m) 2 − 5i. (n) 1 + i. (o) 1 −i. (p) 5 + 2i.
18.3. Using polar coordinates, show that:
(a)(−1+i)
7
= −8(1 + i). (b)(1+i
√
3)
−10
=2
−11
(−1+i
√
3).
18.4. Find the real and imaginary parts of the following:
(a) (1 + i
√
3)
3
. (b) (2 + i)
53
. (c)
4
√
i. (d)
3
1+i
√
3.
(e) (1 + i
√
3)
63
. (f)
1 − i
1+i
81
. (g)
6
√
−i. (h)
4
√
−1.
(i)
1+i
√
3
√
3+i
217
. (j) (1 + i)
22
. (k)
6
√
1 − i. (l) (1 − i)
4
.
18.5. Find the Cartesian form of all complex numbers z which satisfy (a)
z
3
+1=0,and(b)z
4
− 16i =0.
18.6. Find the absolute value of
3+4i
3 − 4i
and
a + ib
a − ib
.
18.7. Derive the following trigonometric identities:
cos 3θ =4cos
3
θ − 3cosθ,
sin 3θ =3sinθ − 4sin
3
θ.
18.8. Show that Equation (18.11) leads to Equation (18.14).
494 Complex Arithmetic
18.9. Show that z is real if and only if z = z
∗
.
18.10. Show that |Re(z)| + |Im(z)|≥|z|≥(|Re(z)|+ |Im(z)|)/
√
2.
18.11. Let z
1
= x
1
+ iy
1
and z
2
= x
2
+ iy
2
represent two planar vectors z
1
and z
2
. Show that
z
1
z
∗
2
= z
1
· z
2
− i
ˆ
e
z
· z
1
× z
2
.
18.12. Sketch the set of points determined by each of the following conditions:
(a) |z −2+i| =2. (b) |z +2i|≤4. (c) |z + i| = |z − i|.
(d) Im(z
∗
+ i)=2. (e) 2z +3z
∗
=1. (f) z
2
+(z
∗
)
2
=2.
Hint: Find a relation between x and y.
18.13. Show that the equation of a circle of radius r centered at z
0
can be
written as |z|
2
− 2Re(zz
∗
0
)=r
2
−|z
0
|
2
.
18.14. Given that z
1
z
2
= 0, show that
(a) Re(z
1
z
∗
2
)=|z
1
||z
2
|,and|z
1
+ z
2
| = |z
1
| + |z
2
|, if and only if arg(z
1
) −
arg(z
2
)=2nπ,forn =0, ±1, ±2,....
(b) What does the second equality mean geometrically?
18.15. Assume that z =1andz
n
= 1. Show that 1 + z + z
2
+ ···+ z
n−1
=0.
18.16. Substitute x + iy for z in z
2
+ z + 1 = 0 and solve the resulting
equations for x and y. Compare these with the roots obtained by solving the
equation in z directly.
18.17. Find the roots of z
4
+ 4 = 0 and use them to factor z
4
+4 into a
product of quadratic polynomials with real coefficients. Hint: First factor
z
4
+ 4 into linear terms.
18.18. Evaluate the following roots and plot them on the complex plane:
(a)
5
√
1+i. (b)
4
√
−1. (c)
8
√
1. (d)
5
√
−32.
(e)
√
3+4i. (f)
3
√
−1. (g)
4
√
−16i. (h)
6
√
−1.
18.19. Use binomial expansion to show directly that
−
1
2
+ i
√
3
2
3
=1 and
−
1
2
− i
√
3
2
3
=1.
18.20. Use
e
ax
= e
ax
/a to find the indefinite integral of sin
2
x.Verifythat
the derivative of your answer is indeed sin
2
x.
18.21. Use
e
ax
= e
ax
/a and e
ibx
=cos(bx)+i sin(bx) to verify the following
relations by integrating a certain complex exponential:
#
e
ax
cos(bx) dx =
e
ax
a
2
+ b
2
[a cos(bx)+b sin(bx)],
#
e
ax
sin(bx) dx =
e
ax
a
2
+ b
2
[a sin(bx) − b cos(bx)],
where a and b are assumed to be real constants.

18.5 Problems 495
18.22. (a) Using
N
k=1
r
k
=(r
N+1
−r)/(r−1), evaluate the sum
N
k=1
e
−iβk
.
In particular, show that
N
k=1
e
i(α−βk)
= e
i(α−β)
e
−iβN
− 1
e
−iβ
− 1
.
(b) Now show that if β =2π/N,then
N
k=1
cos(α − βk)=0=
N
k=1
sin(α −βk).
18.23. Express cos 4θ and sin 4θ in terms of powers of cos θ and sin θ.
18.24. Use mathematical induction to show the de Moivre theorem.
18.25. Using binomial expansion and the de Moivre theorem, show that
cos nθ =
[n/2]
m=0
(−1)
m
n
2m
sin
2m
θ cos
n−2m
θ,
sin nθ =
[n/2]
m=0
(−1)
m
n
2m +1
sin
2m+1
θ cos
n−2m−1
θ,
where [x] stands for the greatest integer less than or equal to x.
18.26. Derive Equation (18.17) from the equations preceding it.
18.27. Find the following sums, where α and β are real:
(a)cosα +cos(α + β)+cos(α +2β)+···+cos(α + nβ).
(b)sinα +sin(α + β)+sin(α +2β)+···+sin(α + nβ).
Hint: Use the result of Problem 18.22.
18.28. Show that
#
b
a
e
2i(n−k)πx/L
=
0
0ifn = k,
L if n = k,
where b = a + L.
18.29. Use Equations (18.20) and (18.21) to obtain Equation (18.22)
18.30. Find the Fourier series expansion of Problem 10.22 using complex
exponentials.
18.31. An electric voltage V (t)isgivenby
V (t)=V
0
sin
πt
2T
, 0 ≤ t ≤ T
and repeats itself with period T . Find the Fourier series expansion of V (t)
using complex exponential functions.

496 Complex Arithmetic
18.32. A periodic voltage is given by the formula
V (t)=
0
V
0
sin(πt/2T )if0≤ t ≤ T,
0ifT ≤ t ≤ 2T,
in the interval (0, 2T ). Find the Fourier series representation of this voltage
using complex exponential functions.
18.33. A periodic voltage with period 4T is given by
V (t)=
⎧
⎨
⎩
V
0
1 −
t
2
T
2
if − T ≤ t ≤ T,
0ifT ≤|t|≤2T.
Write the Fourier series of V (t) using complex exponential functions.
18.34. The function f (x) is given by the integral
f(x)=
#
∞
−∞
g(y)e
ixy
dy.
Find g(y)asanintegraloverf(x). Hint: Multiply both sides of the equation
by e
−ixz
and integrate over x, changing the order of integration on the right-
hand side and using (18.28).

Chapter 19
Complex Derivative
and Integral
So far we have concerned ourselves with the algebra of the complex numbers.
The subject of complex analysis is extremely rich and important. The scope
and the level of this book does not allow a comprehensive treatment of complex
analysis. Therefore, we shall briefly review some of the more elementary
topics and encourage the reader to refer to more advanced books for a more
comprehensive treatment. We start here, as is done in real analysis, with the
notion of a function.
19.1 Complex Functions
A complex function f(z) is a rule that associates one complex number to
another. We write f(z)=w where both z and w are complex numbers. The
graph of a
complex function
is impossible to
visualize because
it lives in a four
dimensional space.
function f can be geometrically thought of as a correspondence between two
complex planes, the z-plane and the w-plane. In the real case, this correspon-
dence can be represented by a graph. It could also be represented by arrows
from one real line (the x-axis) to another real line (the y-axis) joining a point
of the first real line to the image point of the second real line. When the
possibility of graph is available, the second representation of real functions
appears prohibitively clumsy! For complex functions, no graph is available,
because one cannot draw pictures in four dimensions!
1
Therefore, the second
alternative is our only choice. The w-plane has a real axis and an imaginary
axis, which we can call u and v, respectively. Both u and v are real functions
of the coordinates of z, i.e., x and y. Therefore, we may write
f(z)=u(x, y)+iv(x, y). (19.1)
1
The “graph” of a complex function would be a collection of pairs (z, f(z)) just as the
graph of a real function is a collection of pairs (x, f(x)). While in the latter case the graph
can be drawn in the (x, y) plane, the former needs four dimensions because both z and f(z)
have two components each.
498 Complex Derivative and Integral
z
w
f
(x, y)
(u, v)
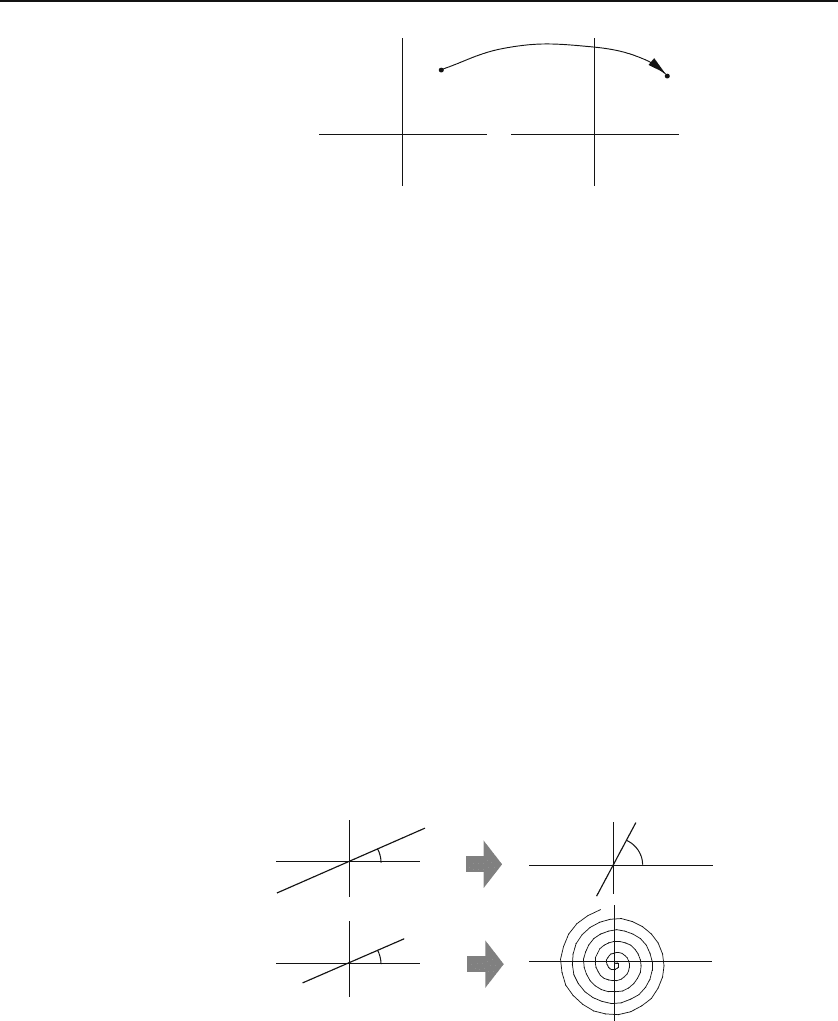
Figure 19.1: Amapfromthez-plane to the w-plane.
This equation gives a unique point (u, v)inthew-plane for each point
(x, y)inthez-plane (see Figure 19.1). Under f ,regionsofthez-plane are
mapped onto regions of the w-plane. For instance, a curve in the z-plane may
be mapped into a curve in the w-plane.
Example 19.1.1.
Let us investigate the behavior of some elementary complex
functions. In particular, we shall look at the way a line y = mx in the z-plane is
mapped to lines and curves in the w-plane by the action of these functions.
(a) Let us start with the simple function w = f(z)=z
2
.Wehave
w =(x + iy)
2
= x
2
− y
2
+2ixy
with u(x, y)=x
2
− y
2
and v(x, y)=2xy.Fory = mx, these equations yield
u =(1− m
2
)x
2
and v =2mx
2
. Eliminating x in these equations, we find v =
[2m/(1 − m
2
)]u. This is a line passing through the origin of the w-plane [see Fig-
ure 19.2(a)]. Note that the angle the line in the w-plane makes with its real axis is
twice the angle the line in the z-plane makes with the x-axis.
(b) Now let us consider w = f(z)=e
z
= e
x+iy
,whichgivesu(x, y)=e
x
cos y
and v(x, y)=e
x
sin y. Substituting y = mx,weobtainu = e
x
cos mx and v =
e
x
sin mx. Unlike part (a), we cannot eliminate x to find v as an explicit func-
tion of u. Nevertheless, the last pair of equations are the parametric equations of
acurve(withx as the parameter) which we can plot in a uv-plane as shown in
Figure 19.2(b).
(a)
α
y
x
2α
u
v
(b)
α
y
x
u
v
Figure 19.2: (a) The map z
2
takes a line with slope angle α and maps it onto a line
withtwicetheangleinthew-plane. (b) The map e
z
takes the same line and maps it
onto a spiral in the w-plane.

19.1 Complex Functions 499
19.1.1 Derivatives of Complex Functions
Limits of complex functions are defined in terms of absolute values. Thus,
lim
z→a
f(z)=w
0
means that, given any real number >0, we can find a
corresponding real number δ>0 such that |f(z)−w
0
| <whenever |z−a| <δ.
Similarly, we say that a function f is continuous at z = a if lim
z→a
f(z)=
f(a), or if there exist >0andδ>0 such that |f(z) − f(a)| <whenever
|z − a| <δ.
The derivative of a complex function is defined as usual:
Definition 19.1.1. Let f(z) be a complex function. The derivative of f at
z
0
is
df
dz
z
0
= lim
Δz→0
f(z
0
+Δz) −f(z
0
)
Δz
provided the limit exists and is independent of Δz.
In this definition “independent of Δz” means independent of Δx and Δy
(the components of Δz) and, therefore, independent of the direction of ap-
proach to z
0
. The restrictions of this definition apply to the real case as well.
For instance, the derivative of f(x)=|x| at x = 0 does not exist because it
approaches +1 from the right and −1fromtheleft.
It can easily be shown that all the formal rules of differentiation that
apply to the real case also apply to the complex case. For example, if f
and g are differentiable, then f ± g, fg, and—as long as g is not zero—f/g
are also differentiable, and their derivatives are given by the usual rules of
differentiation.
Box 19.1.1. Afunctionf(z) is called analytic at z
0
if it is differentiable
at z
0
and at all other points in some neighborhood of z
0
.Apointatwhich
f is analytic is called a regular point of f .Apointatwhichf is not
analytic is called a singular point or a singularity of f. A function for
which all points in C are regular is called an entire function.
Example 19.1.2. Let us examine the derivative of f(z)=x +2iy at z =0: example
illustrating
path-dependence
of derivative
df
dz
z=0
= lim
Δz→0
f(Δz) −f(0)
Δz
= lim
Δx→0
Δy→0
Δx +2iΔy
Δx + iΔy
.
In general, along a line that goes through the origin, y = mx, the limit yields
df
dz
z=0
= lim
Δx→0
Δx +2imΔx
Δx + imΔx
=
1+2im
1+im
.
This indicates that we get infinitely many values for the derivative depending on
the value we assign to m—corresponding to different directions of approach to the
origin. Thus, the derivative does not exist at z =0.
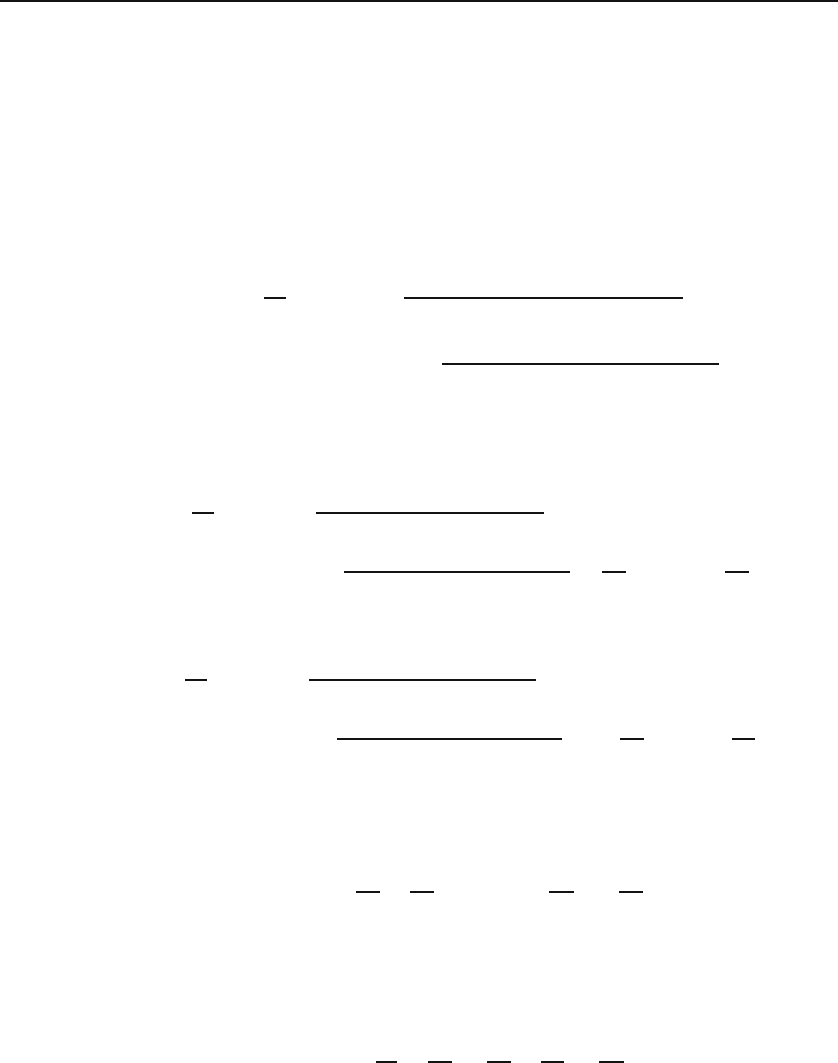
500 Complex Derivative and Integral
A question arises naturally at this point: Under what conditions does
the limit in the definition of derivative exist? We will find the necessary
and sufficient conditions for the existence of that limit. It is clear from the
definition that differentiability puts a severe restriction on f(z) because it
requires the limit to be the same for all paths going through z
0
,thepoint
at which the derivative is being calculated. Another important point to keep
in mind is that differentiability is a local property. To test whether or not a
function f (z) is differentiable at z
0
,wemoveawayfromz
0
by a small amount
Δz and check the existence of the limit in Definition 19.1.1.
For f (z)=u(x, y)+iv(x, y), Definition 19.1.1 yields
df
dz
z
0
= lim
Δx→0
Δy→0
(
u(x
0
+Δx, y
0
+Δy) − u(x
0
,y
0
)
Δx + iΔy
+ i
v(x
0
+Δx, y
0
+Δy) −v(x
0
,y
0
)
Δx + iΔy
)
.
If this limit is to exist for all paths, it must exist for the two particular paths
on which Δy = 0 (parallel to the x-axis) and Δx = 0 (parallel to the y-axis).
For the first path we get
df
dz
z
0
= lim
Δx→0
u(x
0
+Δx, y
0
) −u(x
0
,y
0
)
Δx
+ i lim
Δx→0
v(x
0
+Δx, y
0
) −v(x
0
,y
0
)
Δx
=
∂u
∂x
(x
0
,y
0
)
+ i
∂v
∂x
(x
0
,y
0
)
.
For the second path (Δx = 0), we obtain
df
dz
z
0
= lim
Δy→0
u(x
0
,y
0
+Δy) − u(x
0
,y
0
)
iΔy
+ i lim
Δy→0
v(x
0
,y
0
+Δy) − v(x
0
,y
0
)
iΔy
= −i
∂u
∂y
(x
0
,y
0
)
+
∂v
∂y
(x
0
,y
0
)
.
If f is to be differentiable at z
0
, the derivatives along the two paths must be
equal. Equating the real and imaginary parts of both sides of this equation
and ignoring the subscript z
0
(x
0
, y
0
,orz
0
is arbitrary), we obtain
∂u
∂x
=
∂v
∂y
and
∂u
∂y
= −
∂v
∂x
. (19.2)
These two conditions, which are necessary for the differentiability of f,are
called the Cauchy–Riemann (C–R) conditions.
Cauchy–Riemann
conditions
The arguments leading to Equation (19.2) imply that the derivative, if it
exists, can be expressed as
df
dz
=
∂u
∂x
+ i
∂v
∂x
=
∂v
∂y
− i
∂u
∂y
. (19.3)
The C–R conditions assure us that these two equations are equivalent.

19.1 Complex Functions 501
Example 19.1.3. Let us examine the differentiability of some complex functions.
(a) We have already established that f(z)=x +2iy is not differentiable at z =0.
We can now show that it is has no derivative at any point in the complex plane. This
is easily seen by noting that u = x and v =2y,andthat∂u/∂x =1= ∂v/∂y =2,
and the first C–R condition is not satisfied. The second C–R condition is satisfied,
but that is not enough.
(b) Now consider f (z)=x
2
−y
2
+2ixy for which u = x
2
−y
2
and v =2xy.TheC–R
conditions become ∂u/∂x =2x = ∂v/∂y and ∂u/∂y = −2y = −∂v/∂x.Thus,f(z)
may be differentiable. Recall that C–R conditions are only necessary conditions; we
do not know as yet if they are also sufficient.
(c) Let u(x, y)=e
x
cos y and v(x, y)=e
x
sin y.Then∂u/∂x = e
x
cos y = ∂v/∂y
and ∂u/∂y = −e
x
sin y = −∂v/∂x and the C–R conditions are satisfied.
The requirement of differentiability is very restrictive: the derivative must
exist along infinitely many paths. On the other hand, the C–R conditions
seem deceptively mild: they are derived for only two paths. Nevertheless,
the two paths are, in fact, true representatives of all paths; that is , the C–R
conditions are not only necessary, but also sufficient. This is the content of
the Cauchy–Riemann theorem which we state without proof:
2
Theorem 19.1.4. (Cauchy–Riemann Theorem). The function f (z)=
u(x, y)+iv(x, y) is differentiable in a region of the complex plane if and only
if the Cauchy–Riemann conditions
∂u
∂x
=
∂v
∂y
and
∂u
∂y
= −
∂v
∂x
are satisfied and all first partial derivatives of u and v are continuous in that
region. In that case
df
dz
=
∂u
∂x
+ i
∂v
∂x
=
∂v
∂y
− i
∂u
∂y
.
The C–R conditions readily lead to
∂
2
u
∂x
2
+
∂
2
u
∂y
2
=0,
∂
2
v
∂x
2
+
∂
2
v
∂y
2
=0, (19.4)
i.e., both real and imaginary parts of an analytic function satisfy the two-
harmonic
functions defined
dimensional Laplace equation [Equations (15.13) and (15.15)]. Such functions
are called harmonic functions.
Example 19.1.5.
Let us consider some examples of derivatives of complex func-
tions.
(a) f(z)=z.
Here u = x and v = y; the C–R conditions are easily shown to hold, and for
2
For a simple proof, see Hassani, S. Mathematical Physics: A Modern Introduction to
Its Foundations, Springer-Verlag, 1999, Chapter 9.

502 Complex Derivative and Integral
any z,wehavedf / d z = ∂u/∂x + i∂v/∂x = 1. Therefore, the derivative exists at all
points of the complex plane, i.e., f(z)=z is entire.
(b) f(z)=z
2
.
Here u = x
2
− y
2
and v =2xy; the C–R conditions hold, and for all points z of the
complex plane, we have df / d z = ∂u/∂x + i∂v/∂x =2x + i2y =2z. Therefore, f(z)
is differentiable at all points. So, f(z)=z
2
is also entire.
(c) f(z)=z
n
for n ≥ 1.
We can use mathematical induction and the fact that the product of two entire
functions is an entire function to show that
d
dz
(z
n
)=nz
n−1
.
(d) f(z)=a
0
+ a
1
z + ···+ a
n−1
z
n−1
+ a
n
z
n
,
where a
i
are arbitrary constants. That f(z) is entire follows directly from (c) and
the fact that the sum of two entire functions is entire.
(e) f(z)=e
z
.
Here u(x, y)=e
x
cos y and v(x, y)=e
x
sin y.Thus,∂u/∂x = e
x
cos y = ∂v/∂y and
∂u/∂y = −e
x
sin y = −∂v/∂x and the C–R conditions are satisfied at every point
(x, y)ofthexy-plane. Furthermore,
df
dz
=
∂u
∂x
+ i
∂v
∂x
= e
x
cos y + ie
x
sin y = e
x
(cos y + i sin y)=e
x
e
iy
= e
x+iy
= e
z
and e
z
is entire as well.
(f) f(z)=1/z.
The derivative can be found to be f
(z)=−1/z
2
which does not exist for z =0.
Thus, z = 0 is a singularity of f(z). However, any other point is a regular point of f.
(g) f(z)=1/ sin z.
This gives df / d z = −cos z/sin
2
z.Thus,f has (infinitely many) singular points at
z = ±nπ for n =0, 1, 2,....
Example 19.1.5 shows that any polynomial in z,aswellastheexponential
function e
z
is entire. Therefore, any product and/or sum of polynomials and
e
z
will also be entire. We can build other entire functions. For instance,
e
iz
and e
−iz
are entire functions; therefore, the complex trigonometric
functions, defined by
complex
trigonometric
functions
sin z =
e
iz
− e
−iz
2i
and cos z =
e
iz
+ e
−iz
2
(19.5)
are also entire functions. Problem 19.7 shows that sin z and cos z have only
real zeros.
The complex hyperbolic functions can be defined similarly:
complex
hyperbolic
functions
sinh z =
e
z
− e
−z
2
and cosh z =
e
z
+ e
−z
2
. (19.6)
Although the sum and product of entire functions are entire, the ratio
is not. For instance, if f (z)andg(z) are polynomials of degrees m and n,
respectively, then for n>0, the ratio f(z)/g(z) is not entire, because at the
zeros of g(z)—which always exist—the derivative is not defined.
