Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

19.1 Complex Functions 503

The functions u(x, y)andv(x, y) of an analytic function have an interesting

property which the following example investigates.

Example 19.1.6.

The family of curves u(x, y) = constant is perpendicular to curves of constant

u and v are

perpendicular.

the family of curves v(x, y) = constant at each point of the complex plane where

f(z)=u + iv is analytic.

This can easily be seen by looking at the normal to the curves. The normal to

the curve u(x, y) = constant is simply ∇u = ∂u/∂x, ∂u/∂y (see Theorem 12.3.2).

Similarly, the normal to the curve v(x, y)=constant is∇v = ∂v/∂x, ∂v/∂y.

Taking the dot product of these two normals, we obtain

(∇u) · (∇v)=

∂u

∂x

∂v

∂x

∂u

∂y

∂v

∂y

∂u

∂x



−

∂u

∂y



∂u

∂y



∂u

∂x



by the C–R conditions.



Historical Notes

One can safely say that rigorous complex analysis was founded by a single man:

Cauchy. Augustin-Louis Cauchy was one of the most inﬂuential French mathe-

maticians of the nineteenth century. He began his career as a military engineer, but

when his health broke down in 1813 he followed his natural inclination and devoted

himself wholly to mathematics.

In mathematical productivity Cauchy was surpassed only by Euler, and his col-

lected works ﬁll 27 fat volumes. He made substantial contributions to number theory

and determinants; is considered to be the originator of the theory of ﬁnite groups;

and did extensive work in astronomy, mechanics, optics, and the theory of elasticity.

Augustin-Louis

Cauchy 1789–1857

His greatest achievements, however, lay in the ﬁeld of analysis. Together with his

contemporaries Gauss and Abel, he was a pioneer in the rigorous treatment of limits,

continuous functions, derivatives, integrals, and inﬁnite series. Several of the basic

tests for the convergence of series are associated with his name. He also provided the

ﬁrst existence proof for solutions of diﬀerential equations, gave the ﬁrst proof of the

convergence of a Taylor series, and was the ﬁrst to feel the need for a careful study

of the convergence behavior of Fourier series. However, his most important work

was in the theory of functions of a complex variable, which in essence he created and

which has continued to be one of the dominant branches of both pure and applied

mathematics. In this ﬁeld, Cauchy’s integral theorem and Cauchy’s integral formula

are fundamental tools without which modern analysis could hardly exist.

Unfortunately, his personality did not harmonize with the fruitful power of his

mind. He was an arrogant royalist in politics and a self-righteous, preaching, pious

believer in religion—all this in an age of republican skepticism—and most of his

fellow scientists disliked him and considered him a smug hypocrite. It might be fairer

to put ﬁrst things ﬁrst and describe him as a great mathematician who happened

also to be a sincere but narrow-minded bigot.

19.1.2 Integration of Complex Functions

We have thus far discussed the derivative of a complex function. The concept

of integration is even more important because, as we shall see later, derivatives

can be written in terms of integrals.

504 Complex Derivative and Integral

The deﬁnite integral of a complex function is naively deﬁned in analogy

to that of a real function. However, a crucial diﬀerence exists: While in the

complex integrals

are

path-dependent.

real case, the limits of integration are real numbers and there is only one way

to connect these two limits (along the real line), the limits of integration of

a complex function are points in the complex plane and there are inﬁnitely

many ways to connect these two points. Thus, we speak of a deﬁnite integral

of a complex function along a path. It follows that complex integrals are, in

general, path-dependent.

f(z) dz = lim

N→∞

Δz

→0



i=1

f(z

)Δz

, (19.7)

where Δz

is a small segment—situated at z

—of the curve that connects the

complex number α

to the complex number α

in the z-plane (see Figure 19.3).

An immediate consequence of this equation is



f(z) dz



= lim

N→∞

Δz

→0





i=1

f(z

)Δz



≤ lim

N→∞

Δz

→0



i=1

|f(z

)Δz

= lim

N→∞

Δz

→0



i=1

|f(z

)||Δz

| =

|f(z)||dz|, (19.8)

where we have used the triangle inequality as expressed in Equation (18.7).

Since there are inﬁnitely many ways of connecting α

to α

, there is no

guarantee that Equation (19.7) has a unique value: It is possible to obtain

diﬀerent values for the integral of some functions for diﬀerent paths. It may

seem that we should avoid such functions and that they will have no use in

physical applications. Quite to the contrary, most functions encountered, will

not, in general, give the same result if we choose two completely arbitrary

paths in the complex plane. In fact, it turns out that the only complex

function that gives the same integral for any two arbitrary points connected

by any two arbitrary paths is the constant function. Because of the importance

of paths in complex integration, we need the following deﬁnition:

Figure 19.3: One of the inﬁnitely many paths connecting two complex points α

and

19.1 Complex Functions 505

Box 19.1.2. A contour is a collection of connected smooth arcs. When

the beginning point of the ﬁrst arc coincides with the end point of the last

one, the contour is said to be a simple closed contour (or just closed

contour).

We encountered path-dependent integrals when we tried to evaluate the

line integral of a vector ﬁeld in Chapter 14. The same argument for path-

independence can be used to prove (see Problem 19.21)

Theorem 19.1.7. (Cauchy–Goursat Theorem).Letf(z) be analytic on

a simple closed contour C and at all points inside C.Then

f(z) dz =0

Equivalently,



f(z) dz is independent of the smooth path connecting α

and

as long as the path lies entirely in the region of analyticity of f (z).

Example 19.1.8.

We consider a few examples of deﬁnite integrals.

(a) Let us evaluate the integral I



zdz where γ

is the straight line drawn

from the origin to the point (1, 2) (see Figure 19.4). Along such a line y =2x and

thus γ

(t)=t +2it where 0 ≤ t ≤ 1, and

zdz=

(t +2it)(dt +2idt)=

(−3tdt +4itdt)=−

+2i.

For a diﬀerent path γ

, along which y =2x

,wegetγ

(t)=t+2it

where 0 ≤ t ≤ 1,

and



zdz=

(t +2it

)(dt +4itdt)=−

+2i.

Therefore, I

= I



. This is what is expected from the Cauchy–Goursat theorem

because the function f(z)=z is analytic on the two paths and in the region bounded

by them.

(1, 2)

Figure 19.4: The three diﬀerent paths of integration corresponding to the integrals I



, I

,andI



We are using the parameterization x = t, y =2x =2t for the curve.

506 Complex Derivative and Integral

(b) Now let us consider I



dz with γ

as in part (a). Substituting for z in

terms of t,weobtain

(t +2it)

(dt +2idt)=(1+2i)

dt = −

−

Next we compare I

with I



dz where γ

is as shown in Figure 19.4. This

path can be described by

(t)=

t for 0 ≤ t ≤ 1,

1+i(t − 1) for 1 ≤ t ≤ 3.

Therefore,



dt +

[1 + i(t −1)]

(idt)=

− 4 −

i = −

−

which is identical to I

, once again because the function is analytic on γ

and γ

well as in the region bounded by them.



dz/z where γ

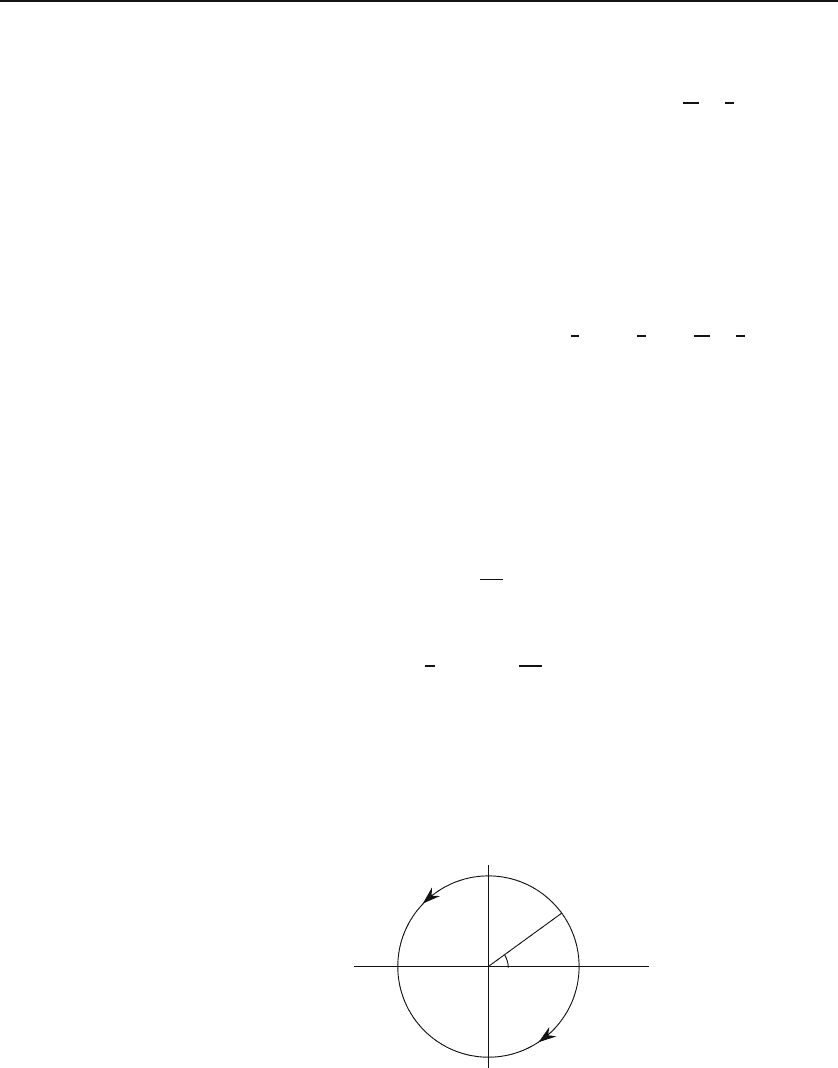
is the upper semicircle of unit radius, as shown in Figure 19.5.

A parametric equation for γ

can be given in terms of θ:

(θ)=cosθ + i sin θ = e

iθ

⇒ dz = ie

iθ

dθ, 0 ≤ θ ≤ π.

Thus, we obtain

iθ

dθ = iπ.

On the other hand,



dz =

2π

iθ

dθ = −iπ.

Here the two integrals are not equal. From γ

and γ



we can construct a counter-

clockwise simple closed contour C, along which the integral of f (z)=1/z becomes

dz/z = I

− I



=2iπ. That the integral is not zero is a consequence of the

fact that 1/z is not analytic at all points of the region bounded by the closed

contour C.



′ γ

r = 1

Figure 19.5: The two semicircular paths for calculating I

and I



19.1 Complex Functions 507

C C

(a)

(b)

Figure 19.6: A contour of integration can be deformed into another contour. The

second contour is usually taken to be a circle because of the ease of its corresponding

integration. (a) shows the original contour, and (b) shows the two contours as well as

the (shaded) region between them in which the function is analytic.

The Cauchy–Goursat theorem applies to more complicated regions. When

a region contains points at which f(z) is not analytic, those points can be

avoided by redeﬁning the region and the contour (Figure 19.6). Such a pro-

cedure requires a convention regarding the direction of “motion” along the

contour. This convention is important enough to be stated separately.

convention for

positive sense of

integration around

aclosedcontour

Box 19.1.3. (Convention). When integrating along a closed contour,

we agree to traverse the contour in such a way that the region enclosed

by the contour lies to our left. An integration that follows this convention

is called integration in the positive sense. Integration performed in the

opposite direction acquires a minus sign.

Suppose that we want to evaluate the integral

f(z) dz where C is some

contour in the complex plane [see Figure 19.6(a)]. Let Γ be another—usually

simpler, say a circle—contour which is either entirely inside or entirely out-

side C. Figure 19.6 illustrates the case where Γ is entirely inside C.We

assume that Γ is such that f (z) does not have any singularity in the region

between C and Γ. By connecting the two contours with a line as shown in

Figure 19.6(b), we construct a composite closed contour consisting of C,Γ,

and twice the line segment L, once in the positive directions and once in

the negative. Within this composite contour, the function f (z)isanalytic.

Therefore, by the Cauchy–Goursat theorem, we have

−

f(z) dz +

f(z) dz −

f(z) dz =0.

The negative sign for C is due to the convention above. It follows from this

equation that the integral along C is the same as that along the circle Γ. This

result can be interpreted by saying that

508 Complex Derivative and Integral

Box 19.1.4. We can always deform the contour of an integral in the com-

plex plane into a simpler contour, as long as in the process of deformation

we encounter no singularity of the function.

19.1.3 Cauchy Integral Formula

One extremely important consequence of the Cauchy–Goursat theorem, the

centerpiece of complex analysis, is the Cauchy integral formula which we state

without proof.

Theorem 19.1.9. Let f(z) be analytic on and within a simple closed contour

C integrated in the positive sense. Let z

be any interior point of C.Then

f(z

2πi

f(z)

z − z

dz.

This is called the Cauchy integral formula (CIF).

Example 19.1.10.

We can use the CIF to evaluate the following integrals:

+3)

(z − i)

− 1) dz

(z −

)(z

− 4)

z/2

(z − iπ)(z

− 20)

where C

, C

,andC

are circles centered at the origin with radii r

, r

=1,

and r

= 4, respectively.

For I

we note that f(z)=z

/(z

+3)

is analytic within and on C

,andz

= i

lies in the interior of C

.Thus,

f(z)dz

z − i

=2πif(i)=2πi

+3)

= −i

Similarly, f(z)=(z

− 1)/(z

− 4)

for I

is analytic on and within C

,andz

is an interior point of C

.Thus,theCIFgives

f(z)dz

z −

=2πif(

)=2πi

− 1

(

− 4)

32π

1125

For the last integral, f (z)=e

z/2

/(z

− 20)

, and the interior point is z

= iπ:

f(z)dz

z −iπ

=2πif(iπ)=2πi

iπ/2

(−π

− 20)

= −

2π

(π

+ 20)



The CIF gives the value of an analytic function at every point inside a

simple closed contour when it is given the value of the function only at points

on the contour. It seems as though analytic functions have no freedom within

why analytic

functions “remote

sense” their values

at distant points

a contour: They are not free to change inside a region once their value is

ﬁxed on the contour enclosing that region. There is an analogous situation in

For a proof, see Hassani, S. Mathematical Physics: A Modern Introduction to Its Foun-

dations, Springer-Verlag, 1999, Chapter 9.

19.1 Complex Functions 509

certain areas of physics, for example, electrostatics: The speciﬁcation of the

potential at the boundaries, such as conductors, automatically determines it

at any other point in the region of space bounded by the conductors. This is

the content of the uniqueness theorem (to be discussed later in this book) used

in electrostatic boundary-value problems. However, the electrostatic potential

Φ is bound by another condition, Laplace’s equation; and the combination of

Laplace’s equation and the boundary conditions furnishes the uniqueness of Φ.

It seems, on the other hand, as though the mere speciﬁcation of an analytic

function on a contour, without any other condition, is suﬃcient to determine

the function’s value at all points enclosed within that contour. This is not

the case. An analytic function, by its very deﬁnition, satisﬁes another re-

strictive condition: Its real and imaginary parts separately satisfy Laplace’s

equation in two dimensions! [see Equation (19.4)]. Thus, it should come as

no surprise that the value of an analytic function at a boundary (contour)

determines the function at all points inside the boundary.

19.1.4 Derivatives as Integrals

The CIF is a very powerful tool for working with analytic functions. One

of the applications of this formula is in evaluating the derivatives of such

functions. It is convenient to change the dummy integration variable to ξ and

write the CIF as

f(z)=

2πi

f(ξ) dξ

ξ − z

, (19.9)

where C is a simple closed contour in the ξ-plane and z is a point within C.

By carrying the derivative inside the integral, we get

2πi

f(ξ) dξ

ξ −z

2πi



f(ξ) dξ

ξ − z



2πi

f(ξ) dξ

(ξ − z)

By repeated diﬀerentiation, we can generalize this formula to the nth deriva-

tive, and obtain

Theorem 19.1.11. The derivatives of all orders of an analytic function f(z)

exist in the domain of analyticity of the function and are themselves analytic

in that domain. The nth derivative of f(z) is given by

(n)

(z)=

2πi

f(ξ) dξ

(ξ − z)

n+1

. (19.10)

Example 19.1.12.

Let us apply Equation (19.10) directly to some simple func-

tions. In all cases, we will assume that the contour is a circle of radius r centered

at z.

(a) Let f(z)=K, a constant. Then, for n =1wehave

2πi

Kdξ

(ξ − z)

510 Complex Derivative and Integral

Since ξ is always on the circle C centered at z, ξ − z = re

iθ

and dξ = rie

iθ

dθ.So

we have

2πi

2π

Kire

iθ

dθ

(re

iθ

)

2πr

2π

−iθ

dθ =0.

That is, the derivative of a constant is zero.

(b) Given f(z)=z, its ﬁrst derivative will be

2πi

ξdξ

(ξ −z)

2πi

2π

(z + re

iθ

)ire

iθ

dθ

(re

iθ

)

2π



2π

−iθ

dθ +

2π

dθ



2π

(0 + 2π)=1.

, for the ﬁrst derivative Equation (19.10) yields

2πi

dξ

(ξ − z)

2πi

2π

(z + re

iθ

)

ire

iθ

dθ

(re

iθ

)

2π

+(re

iθ

)

+2zre

iθ

(re

iθ

)

−1

dθ

2π



2π

−iθ

dθ + r

2π

iθ

dθ +2z

2π

dθ



=2z.

Itcanbeshownthat,ingeneral,(d/dz)z

= mz

m−1

. The proof is left as Problem

19.24.



The CIF is a central formula in complex analysis. However, due to space

limitations, we cannot explore its full capability here. Nevertheless, one of its

applications is worth discussing at this point. Suppose that f is a bounded

entire function and consider

2πi

f(ξ) dξ

(ξ − z)

Since f is analytic everywhere in the complex plane, the closed contour C can

be chosen to be a very large circle of radius R with center at z.Takingthe

absolute value of both sides yields



2π



2π

f(z + Re

iθ

)

(Re

iθ

)

iRe

iθ

dθ



≤

2π

|f(z + Re

iθ

dθ ≤

2π

dθ =

where we used Equation (19.8) and |e

iθ

| =1. M is the maximum of the

function in the complex plane.

Now as R →∞, the derivative goes to zero.

The only function whose derivative is zero is the constant function. Thus

Box 19.1.5. A bounded entire function is necessarily a constant.

M exists because f is assumed to be bounded.

19.2 Problems 511

There are many interesting and nontrivial real functions that are bounded and

have derivatives (of all orders) on the entire real line. For instance, e

−x

is such any nontrivial

function is either

unbounded or not

entire.

a function. No such freedom exists for complex analytic functions according

to Box 19.1.5! Any nontrivial analytic function is either not bounded (goes

to inﬁnity somewhere on the complex plane) or not entire [it is not analytic

at some point(s) of the complex plane].

A consequence of Proposition 19.1.5 is the fundamental theorem of

algebra which states that any polynomial of degree n ≥ 1hasn roots (some

fundamental

theorem of algebra

proved

of which may be repeated). In other words, the polynomial

p(x)=a

+ a

x + ···+ a

for n ≥ 1

can be factored completely as p(x)=c(x −z

)(x − z

) ...(x − z

)wherec is

a constant and the z

are, in general, complex numbers.

To see how Proposition 19.1.5 implies the fundamental theorem of algebra,

we let f(z)=1/p(z) and assume the contrary, i.e., that p(z) is never zero for

any (ﬁnite) z.Thenf(z) is bounded and analytic for all z, and Proposition

19.1.5 says that f(z) is a constant. This is obviously wrong. Thus, there must

be at least one z,sayz = z

,forwhichp(z) is zero. So, we can factor out

(z −z

)fromp(z)andwritep(z)=(z −z

)q(z)whereq(z)isofdegreen −1.

Applying the above argument to q(z), we have p(z)=(z − z

)(z − z

)r(z)

where r(z)isofdegreen −2. Continuing in this way, we can factor p(z)into

linear factors. The last polynomial will be a constant (a polynomial of degree

zero) which we have denoted as c.

19.2 Problems

19.1. Show that f(z)=z

maps a line that makes an angle α with the

real axis of the z-plane onto a line in the w-plane which makes an angle

2α with the real axis of the w-plane. Hint: Use the trigonometric identity

tan 2α =2tanα/(1 −tan

α).

19.2. Show that the function w =1/z maps the straight line y =

in the

z-plane onto a circle in the w-plane.

19.3. (a) Using the chain rule, ﬁnd ∂f/∂z

∗

and ∂f/∂z in terms of partial

derivatives with respect to x and y.

(b) Evaluate ∂f/∂z

∗

and ∂f/∂z assuming that the C–R conditions hold.

19.4. (a) Show that, when z is represented by polar coordinates, the C–R

conditions on a function f(z)are

∂U

∂r

∂V

∂θ

∂U

∂θ

= −r

∂V

∂r

where U and V are the real and imaginary parts of f(z) written in polar

coordinates.

512 Complex Derivative and Integral

(b) Show that the derivative of f can be written as

= e

−iθ



∂U

∂r

+ i

∂V

∂r



Hint: Start with the C–R conditions in Cartesian coordinates and apply the

chain rule to them using x = r cos θ and y = r sin θ.

19.5. Prove the following identities for diﬀerentiation by ﬁnding the real

and imaginary parts of the function—u(x, y)andv(x, y)—and diﬀerentiat-

ing them:

(a)

(f + g)=

. (b)

(fg)=

g + f

(c)







(z)g(z) − g



(z)f (z)

[g(z)]

, where g(z) =0.

19.6. Show that d/dz(ln z)=1/z.Hint:Findu(x, y)andv(x, y)forlnz

using the exponential representation of z, then diﬀerentiate them.

19.7. Show that sin z and cos z have only real roots. Hint: Use deﬁnition of

sine and cosine in terms of exponentials.

19.8. Use mathematical induction and the product rule for diﬀerentiation to

show that

)=nz

n−1

19.9. Use Equations (19.5) and (19.6), to establish the following identities:

(a) Re(sin z)=sinx cosh y, Im(sin z)=cosx sinh y.

(b) Re(cos z)=cosx cosh y, Im(cos z)=−sin x sinh y.

(d) Re(cosh z)=coshx cos y, Im(cosh z)=sinhx sin y.

(e) |sin z|

=sin

x +sinh

y, |cos z|

=cos

x +sinh

(f) |sinh z|

=sinh

x +sin

y, |cosh z|

=sinh

x +cos

19.10. Find all the zeros of sinh z and cosh z.

19.11. Verify the following trigonometric identities:

(a) cos

z +sin

z =1.

(b) cos(z

+ z

)=cosz

cos z

− sin z

sin z

+ z

)=sinz

cos z

+cosz

sin z

(d) sin



− z



=cosz, cos



− z



=sinz.

(e) cos 2z =cos

z − sin

z, sin 2z =2sinz cos z.

(f) tan(z

+ z

tan z

+tanz

1 − tan z

tan z