Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

19.2 Problems 513

19.12. Verify the following hyperbolic identities:

(a) cosh

z − sinh

z =1.

(b) cosh(z

+ z

)=coshz

cosh z

+sinhz

sinh z

+ z

)=sinz

cosh z

+coshz

sinh z

(d) cosh 2z =cosh

z +sinh

z, sinh 2z =2sinhz cosh z.

(e) tanh(z

+ z

tanh z

+tanhz

1+tanhz

tanh z

19.13. Show that

(a)tanh





sinh x + i sin y

cosh x +cosy

. (b) coth





sinh x −i sin y

cosh x − cos y

19.14. Prove the following identities:

(a) cos

−1

z = −i ln(z ±



− 1). (b) sin

−1

z = −i ln[iz ±



1 − z

)].

−1

z =



i − z

i + z



. (d) cosh

−1

z =ln(z ±



− 1).

(e) sinh

−1

z =ln(z ±



+1). (f) tanh

−1

z =



1+z

1 − z



19.15. Prove that exp(z

∗

) is not analytic anywhere.

19.16. Show that e

=cosz + i sin z for any z.

19.17. Show that both the real and imaginary parts of an analytic function

are harmonic.

19.18. Show that each of the following functions—call each one u(x, y)—

is harmonic, and ﬁnd the function’s harmonic partner, v(x, y), such that

u(x, y)+iv(x, y) is analytic. Hint: Use C–R conditions.

(a) x

− 3xy

. (b) e

cos y. (c)

+ y

where x

+ y

=0.

(d) e

−2y

cos 2x. (e) e

−x

cos 2xy.

(f) e

(x cos y − y sin y)+2sinhy sin x + x

− 3xy

+ y.

19.19. Describe the curve deﬁned by each of the following equations:

(a) z =1− it, 0 ≤ t ≤ 2. (b) z = t + it

, −∞ <t<∞.

≤ t ≤

3π

. (d) z = t +

−∞<t<0.

19.20. Let f(z)=w = u + iv. Suppose that

∂

∂x

∂

∂y

= 0. Show that if f

is analytic, then

∂

∂u

∂

∂v

= 0. That is, analytic functions map harmonic

functions in the z-plane to harmonic functions in the w-plane.

514 Complex Derivative and Integral

19.21. (a) Show that



f(z) dz can be written as

A · dr + i

B · dr,

where A = u, −v, 0, B = v, u, 0,anddr = dx, dy, 0.

(b) Show that both A and B have vanishing curls when f is analytic.

19.22. Find the value of the integral



[(z +2)/z] dz,whereC is: (a) the

semicircle z =2e

iθ

,for0≤ θ ≤ π; (b) the semicircle z =2e

iθ

,forπ ≤ θ ≤ 2π;

and (c) the circle z =2e

iθ

,for−π ≤ θ ≤ π.

19.23. Evaluate the integral



dz/(z −1 −i)whereγ is: (a) the line joining

=2i and z

= 3; and (b) the path from z

to the origin and from there to

19.24. Use Equation (19.10) to show that

)=mz

m−1

.Hint:Usethe

binomial theorem.

19.25. Let C be the boundary of a square whose sides lie along the lines

x = ±3andy = ±3. For the positive sense of integration, evaluate each of

the following integrals by using CIF or the derivative formula (19.10):

(a)

−z

z − iπ/2

dz. (b)

z(z

+ 10)

dz. (c)

cos z

(z −

)(z

− 10)

dz.

(d)

sinh z

dz. (e)

cosh z

dz. (f)

cos z

dz.

(g)

cos z

(z − iπ/2)

dz. (h)

(z − iπ)

dz. (i)

cos z

z + iπ

dz.

(j)

− 5z +4

dz. (k)

sinh z

(z − iπ/2)

dz. (l)

cosh z

(z − π/2)

dz.

(m)

(z − 2)(z

− 10)

dz.

Chapter 20

Complex Series

As in the real case, representation of functions by inﬁnite series of “simpler”

functions is an endeavor worthy of our serious consideration. We start with

an examination of the properties of sequences and series of complex numbers

and derive series representations of some complex functions. Most of the

discussion is a direct generalization of the results of the real series.

A sequence {z

}

∞

k=1

of complex numbers is said to converge to a limit z if sequence,

convergence to a

limit, partial sums,

and series

lim

k→∞

|z − z

| = 0. In other words, for each positive number ε there must

exist an integer N such that |z − z

| <εwhenever k>N.Thereadermay

show that the real (imaginary) part of the limit of a sequence of complex

numbers is the limit of the real (imaginary) part of the sequence. Series can

be converted into sequences by partial summation. For instance, to study

the inﬁnite series



∞

k=1

, we form the partial sums Z

≡



k=1

and

investigate the sequence {Z

}

∞

n=1

. We thus say that the inﬁnite series



∞

k=1

converges to Z if lim

n→∞

= Z.

Example 20.0.1.

A series that is used often in analysis is the geometric series

Z =



∞

k=0

. Let us show that this series converges to 1/(1 −z)for|z| < 1. For a

partial sum of n terms, we have

≡



k=0

=1+z + z

+ ···+ z

Multiply this by z and subtract the result from the Z

sum to get (see also Example

9.3.3)

− zZ

=1− z

n+1

⇒ Z

1 − z

n+1

1 − z

We now show that Z

converges to Z =1/(1 − z). We have

|Z − Z

| =



1 − z

−

1 − z

n+1

1 − z



n+1

1 − z



|z|

n+1

|1 − z|

and

lim

n→∞

|Z − Z

| = lim

n→∞

|z|

n+1

|1 − z|

lim

n→∞

|z|

n+1

for |z| < 1. Thus,



∞

k=0

=1/(1 − z)for|z| < 1.



516 Complex Series

If the series



∞

k=0

converges, both the real part,



∞

k=0

,andthe

imaginary part,



∞

k=0

, of the series also converge. From Chapter 9, we

know that a necessary condition for the convergence of the real series



∞

k=0

and



∞

k=0

is that x

→ 0andy

→ 0. Thus, a necessary condition for

the convergence of the complex series is lim

k→∞

= 0. The terms of such a

series are, therefore, bounded. Thus, there exists a positive number M such

that |z

| <M for all k.

A complex series is said to converge absolutely,ifthereal series

absolute

convergence

∞



k=0

| =

∞



k=0



+ y

converges. Clearly, absolute convergence implies convergence.

20.1 Power Series

We now concentrate on the power series which, as in the real case, are inﬁnite

sums of powers of (z − z

). It turns out—as we shall see shortly—that for

complex functions, the inclusion of negative powers is crucial.

power series

Theorem 20.1.1. If the power series



∞

k=0

(z − z

)

converges for z

(assumed to be diﬀerent from z

), then it converges absolutely for every value

of z such that |z −z

| < |z

−z

|. Similarly if the power series



∞

k=0

/(z −

)

converges for z

= z

, then it converges absolutely for every value of z

such that |z −z

| > |z

− z

Proof. We prove the ﬁrst part of the proposition; the second part is done

similarly. Since the series converges for z = z

,alltheterms|a

− z

)

are smaller than a positive number M. We, therefore have

∞



k=0

(z − z

)

| =

∞



k=0



− z

)

(z − z

)

− z

)



∞



k=0

− z

)



z − z

− z



≤

∞



k=0

= M

∞



k=0

1 − B

where B ≡|(z − z

)/(z

− z

)| is a positive real number less than 1. Since

the RHS is a ﬁnite (positive) number, the series of absolute values converges,

and the proof is complete.

The essence of Theorem 20.1.1 is that if a power series—with positive

powers—converges for a point at a distance r

from z

,thenitconvergesfor

all interior points of a circle of radius r

centered at z

. Similarly, if a power

series—with negative powers—converges for a point at a distance r

from z

then it converges for all exterior points of a circle of radius r

centered at z

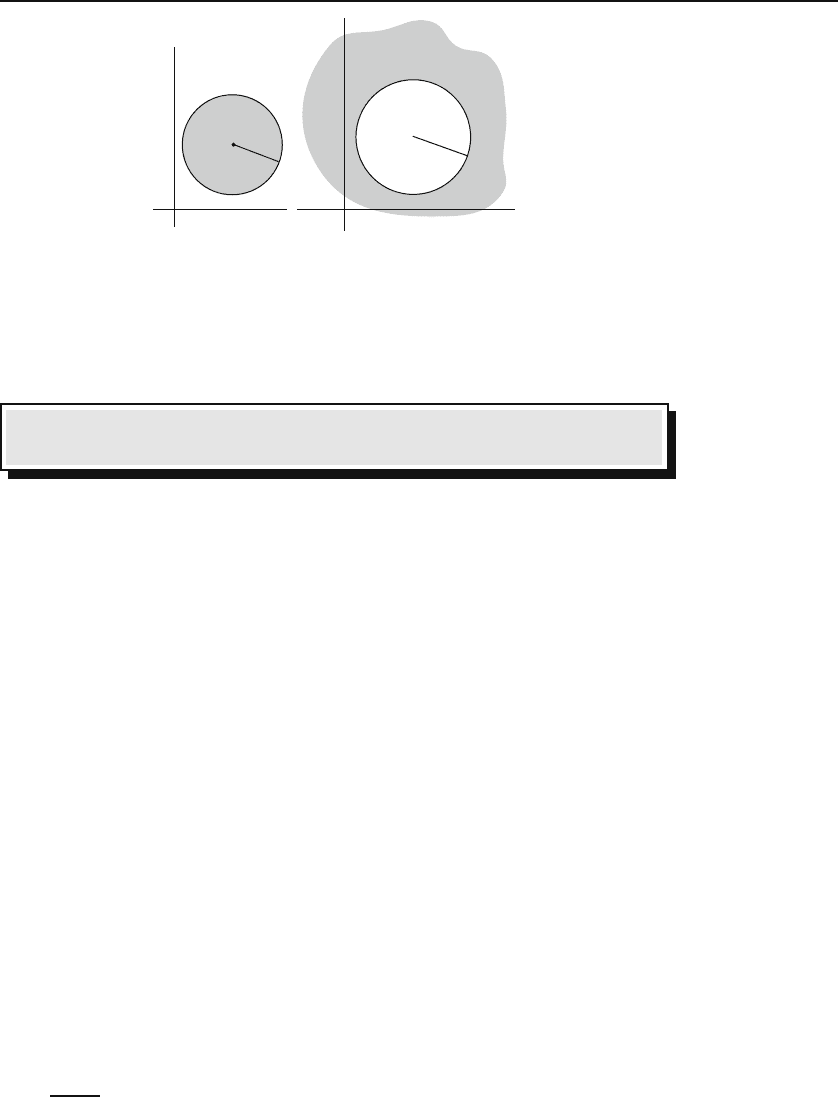
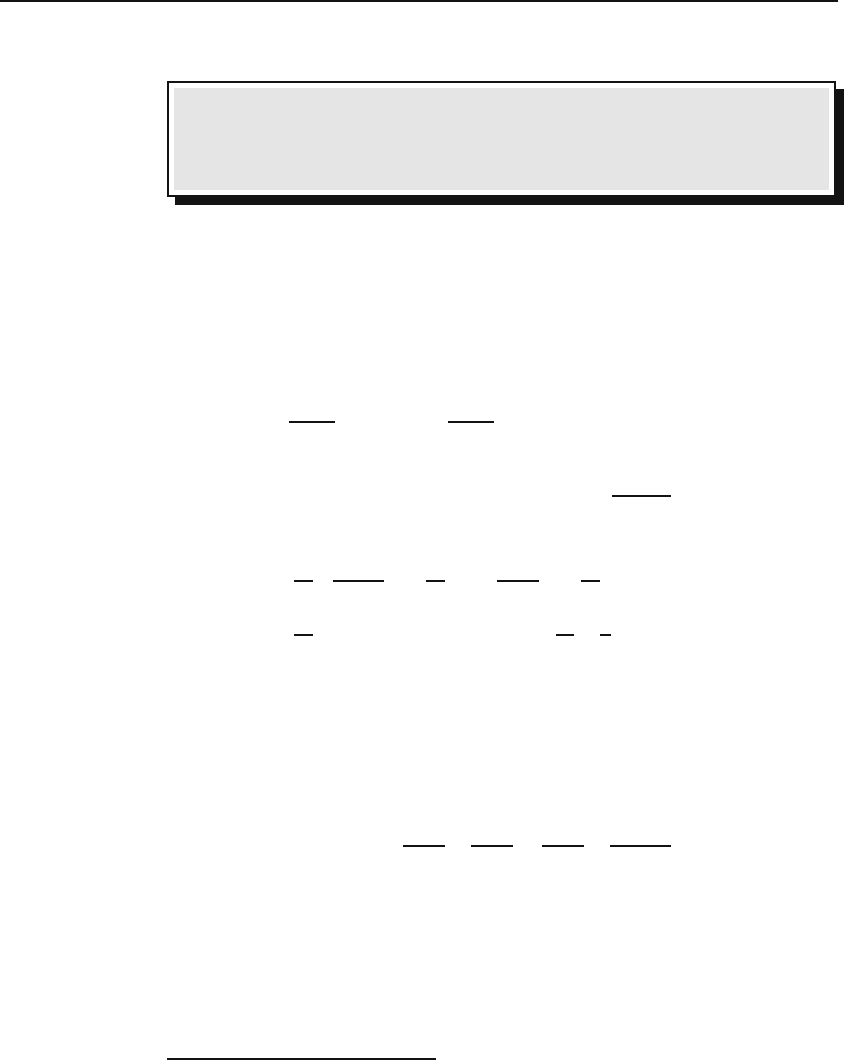
(see Figure 20.1).

20.1 Power Series 517

(a)

(b)

Figure 20.1: (a) Power series with positive exponents converge for the interior points

of a circle. (b) Power series with negative exponents converge for the exterior points of

a circle.

Box 20.1.1. When constructing power series, positive powers are used

for points inside a circle and negative powers for points outside it.

The largest circle about z

such that the ﬁrst power series of Theorem

20.1.1 converges is called the circle of convergence of the power series. It

circle of

convergence

follows from Theorem 20.1.1 that the series cannot converge at any point

outside the circle of convergence. (Why?)

Let us consider the power series

S(z) ≡

∞



k=0

(z − z

)

(20.1)

which we assume to be convergent at all points interior to a circle for which

|z − z

| = r. This implies that the sequence of partial sums {S

(z)}

∞

n=0

converges. Therefore, for any ε>0, there exists an integer N

such that

|S(z) − S

(z)| <ε whenever n>N

In general, the integer N

may be dependent on z; that is, for diﬀerent values uniform

convergence

explained

of z, we may be forced to pick diﬀerent N

’s. When N

is independent of z,we

say that the convergence is uniform. We state the following result without

proof:

a power series is

uniformly

convergent and

analytic; it can be

diﬀerentiated and

integrated term by

term.

Theorem 20.1.2. The power series S(z)=



∞

n=0

(z −z

)

is uniformly

convergent for all points within its circle of convergence, and S(z) is an ana-

lytic function of z there. Furthermore, such a series can be diﬀerentiated and

integrated term by term:

dS(z)

∞



n=1

(z − z

)

n−1

S(z) dz =

∞



n=0

(z − z

)

dz,

518 Complex Series

at each point z and each path γ located inside the circle of convergence of the

power series.

By substituting the reciprocal of (z −z

) in the power series, we can show

that if



∞

k=0

/(z −z

)

is convergent in the annulus r

< |z −z

| <r

,then

it is uniformly convergent for all z in that annulus, and the series represents

a continuous function of z there.

20.2 Taylor and Laurent Series

Complex series, just as their real counterparts, ﬁnd their most frequent utility

in representing well-behaved functions. The following theorem, which we state

without proof,

is essential in the application of complex analysis.

Theorem 20.2.1. Let C

and C

be circles of radii r

and r

,bothcentered

at z

in the z-plane with r

.Letf(z) be analytic on C

and C

and

throughout S, the annular region between the two circles. Then, at each point

z of S, f(z) is given uniquely by the Laurent series

f(z)=

∞



n=−∞

(z − z

)

, where a

2πi

f(ξ)

(ξ − z

)

n+1

dξ,

and C is any contour within S that encircles z

.Whenr

=0,theseriesis

called Taylor series. In that case a

=0for negative n and a

= f

(n)

)/n!

for n ≥ 0.

We can see the reduction of the Laurent series to Taylor series as follows.

The Laurent expansion is convergent as long as r

< |z − z

| <r

.Inpartic-

ular, if r

= 0, and if the function is analytic throughout the interior of the

larger circle, then f (ξ)/(ξ −z

)

n+1

will be analytic for negative integer n,and

the integral will be zero by the Cauchy–Goursat theorem. Therefore, a

will

be zero for n = −1, −2,.... Thus, only positive powers of (z − z

) will be

present in the series, and we obtain the Taylor series.

For z

= 0, the Taylor series reduces to the Maclaurin series:Maclaurin series

f(z)=f(0) + f



(0)z + ···=

∞



n=0

(n)

(0)

Box 19.1.4 tells us that we can enlarge C

and shrink C

until we encounter

a point at which f is no longer analytic. Thus, we can include all the possible

analytic points by enlarging C

and shrinking C

Example 20.2.2.

Let us expand some functions in terms of series. For entire

functions there is no point in the entire complex plane at which they are not analytic.

For a proof, see Hassani, S. Mathematical Physics: A Modern Introduction to Its Foun-

dations, Springer-Verlag, 1999, Section 9.6.

20.2 Taylor and Laurent Series 519

Thus, only positive powers of (z − z

) will be present, and we will have a Taylor

expansion that is valid for all values of z.

(a) We expand e

around z

=0. Thenth derivative of e

is e

.Thus,f

(n)

(0) = 1,

and the Taylor (Maclaurin) expansion gives

∞



n=0

(n)

(0)

∞



n=0

(b) The Maclaurin series for sin z is obtained by noting that

sin z



z=0

0ifn is even,

(−1)

(n−1)/2

if n is odd,

and substituting this in the Maclaurin expansion:

sin z =



n odd

(−1)

(n−1)/2

∞



k=0

(−1)

2k+1

(2k +1)!

Similarly, we can obtain

cos z =

∞



k=0

(−1)

(2k)!

, sinh z =

∞



k=0

2k+1

(2k +1)!

, cosh z =

∞



k=0

(2k)!

It is seen that the series representation of all these functions is obtained by replacing

the real variable x in their real series representation with a complex variable z.

us ﬁnd the Maclaurin expansion of this function. Starting from the origin (z

=0),

the function is analytic within all circles of radii r<1. At r =1weencountera

singularity, the point z = −1. Thus, the series converges for all points z for which

|z| < 1.

For such points we have

(n)

(0) =

[(1 + z)

−1

]



z=0

=(−1)

n!.

Thus,

1+z

∞



n=0

(n)

(0)

∞



n=0

(−1)



The Taylor and Laurent series allow us to express an analytic function as

a power series. For a Taylor series of f(z) the expansion is routine because

the coeﬃcient of its nth term is simply f

(n)

)/n!, where z

is the center of

the circle of convergence. However, when a Laurent series is applicable in a

there is only one

Laurent series for

a given function

deﬁned in a given

region.

given region of the complex plane, the nth coeﬃcient is not, in general, easy to

evaluate. Usually it can be found by inspection and certain manipulations of

other known series. Then the uniqueness of Laurent series expansion assures

us that the series so obtained is the unique Laurent series for the function in

that region.

As remarked before, the series diverges for all points outside the circle |z| =1. This

does not mean that the function cannot be represented by a series for points outside the

circle. On the contrary, we shall see shortly that the Laurent series, with negative powers

is designed precisely for such a purpose.

See Hassani, S. Mathematical Physics: A Modern Introduction to Its Foundations,

Springer-Verlag, 1999, p. 258.

520 Complex Series

As in the case of real series,we can add,

subtract, and

multiply

convergent power

series.

Box 20.2.1. We can add, subtract, and multiply convergent power series.

Furthermore, if the denominator does not vanish in a neighborhood of a

point z

, then we can obtain the Laurent series of the ratio of two power

series about z

by long division.

Thus converging power series can be manipulated as though they were

ﬁnite sums (polynomials). Such manipulations are extremely useful when

dealing with Taylor and Laurent expansions in which the straightforward cal-

culation of coeﬃcients may be tedious. The following examples illustrate the

power of inﬁnite-series arithmetic. In these examples, the following equations

are very useful:

1 − z

∞



n=0

1+z

∞



n=0

(−1)

, |z| < 1. (20.2)

Example 20.2.3.

To expand the function f(z)=

2+3z

+ z

in a Laurent series

about z =0,rewriteitas

f(z)=



2+3z

1+z





3 −

1+z





3 −

∞



n=0

(−1)



(3 − 1+z − z

+ z

−···)=

− 1+z − z

+ ··· .

This series converges for 0 < |z| < 1. We note that negative powers of z are also

present. This is a reﬂection of the fact that the function is not analytic inside the

entire circle |z| =1;itdivergesatz =0.



Example 20.2.4. The function f(z)=z/[(z − 1)(z −2)] has a Taylor expansion

around the origin for |z| < 1. To ﬁnd this expansion, we write

f(z)=−

z − 1

z − 2

1 − z

−

1 − z/2

Expanding both fractions in geometric series (both |z| and |z/2| are less than 1), we

obtain f(z)=



∞

n=0

−



∞

n=0

(z/2)

. Adding the two series yields

f(z)=

∞



n=0

(1 − 2

−n

for |z| < 1.

This is the unique Taylor expansion of f(z) within the circle |z| =1.

We could, of course, evaluate the derivatives of all orders of the function at z =0and

use the Maclaurin formula. However, the present method gives the same result much more

quickly.

20.2 Taylor and Laurent Series 521

For the annular region 1 < |z| < 2 we have a Laurent series. This can be seen

by noting that

f(z)=

1/z

1/z − 1

−

1 − z/2

= −



1 − 1/z



−

1 − z/2

Since both fractions on the RHS are analytic in the annular region (|1/z| < 1,

|z/2| < 1), we get

f(z)=−

∞



n=0





−

∞



n=0





= −

∞



n=0

−n−1

−

∞



n=0

−n

= −

−∞



n=−1

−

∞



n=0

−n

= −

∞



n=−∞

where a

= −1forn<0anda

= −2

−n

for n ≥ 0. This is the unique Laurent

expansion of f(z)inthegivenregion.

Finally, for |z| > 2wehaveonlynegativepowersofz. We obtain the expansion

in this region by rewriting f(z) as follows:

f(z)=−

1/z

1 − 1/z

2/z

1 − 2/z

Expanding the fractions yields

f(z)=−

∞



n=0

−n−1

∞



n=0

n+1

−n−1

∞



n=0

n+1

− 1)z

−n−1

This is again the unique expansion of f (z) in the region |z| > 2.



The example above shows that a single function may have diﬀerent series

representations in diﬀerent regions of the complex plane, each series having

its own region of convergence.

Example 20.2.5.

Deﬁne f(z)as

f(z)=

(1 − cos z)/z

for z =0,

for z =0.

We can show that f(z) is an entire function.

Since 1 − cos z and z

are entire functions, their ratio is analytic everywhere

except at the zeros of its denominator. The only such zero is z =0. Thus,f(z)is

analytic everywhere except possibly at z = 0. To see the behavior of f(z)atz =0,

we look at its Maclaurin series:

1 − cos z =1−

∞



n=0

(−1)

(2n)!

which implies that

1 − cos z

∞



n=1

(−1)

n+1

2n−2

(2n)!

−

−···.

The expansion on the RHS shows that the value of the series is

, which, by deﬁni-

tion, is f(0). Thus, the series converges for all z, and Box 20.1.2 says that f (z)is

entire.



522 Complex Series

A Laurent series can give information about the integral of a function

around a closed contour in whose interior the function may not be analytic.

In fact, the coeﬃcient of the ﬁrst negative power in a Laurent series is given by

−1

2πi

f(ξ) dξ. (20.3)

Thus,

Box 20.2.2. To ﬁnd the integral of a (nonanalytic) function around a

closed contour surrounding z

, write the Laurent series for the function

andreadoﬀa

−1

, the coeﬃcient of the 1/(z − z

) term. The integral is

2πia

−1

Example 20.2.6. As an illustration of this idea, let us evaluate the integral I =

dz/[z

(z −2)], where C is a circle of radius 1 centered at the origin. The function

is analytic in the annular region 0 < |z| < 2. We can, therefore, expand it as a

Laurent series about z = 0 in that region:

(z −2)

= −



1 − z/2



= −

∞



n=0





= −





−





−

−···.

Thus, a

−1

= −

,and

dz/[z

(z − 2)] = 2πia

−1

= −iπ/2. Any other way of

evaluating the integral is nontrivial.



20.3 Problems

20.1. Expand sinh z in a Taylor series about the point z = iπ.

20.2. Let C be the circle |z − i| = 3 integrated in the positive sense. Find

the value of each of the following integrals using the CIF or the derivative

formula (19.10):

(a)

+ π

dz. (b)

sinh z

+ π

)

dz. (c)

(d)

+9)

. (e)

cosh z

+ π

)

dz. (f)

− 3z +4

− 4z +3

dz.

20.3. For 0 <r<1, show that

∞



k=0

cos kθ =

1 − r cos θ

1+r

− 2r cos θ

and

∞



k=0

sin kθ =

r sin θ

1+r

− 2r cos θ