Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


546 From PDEs to ODEs
These equations constitute the most general set of ODEs resulting from the
separation of the PDE of Equation (22.9) in Cartesian coordinates.
Example 22.2.1.
Let us consider a few cases for which (22.11) or (22.12) is
applicable.
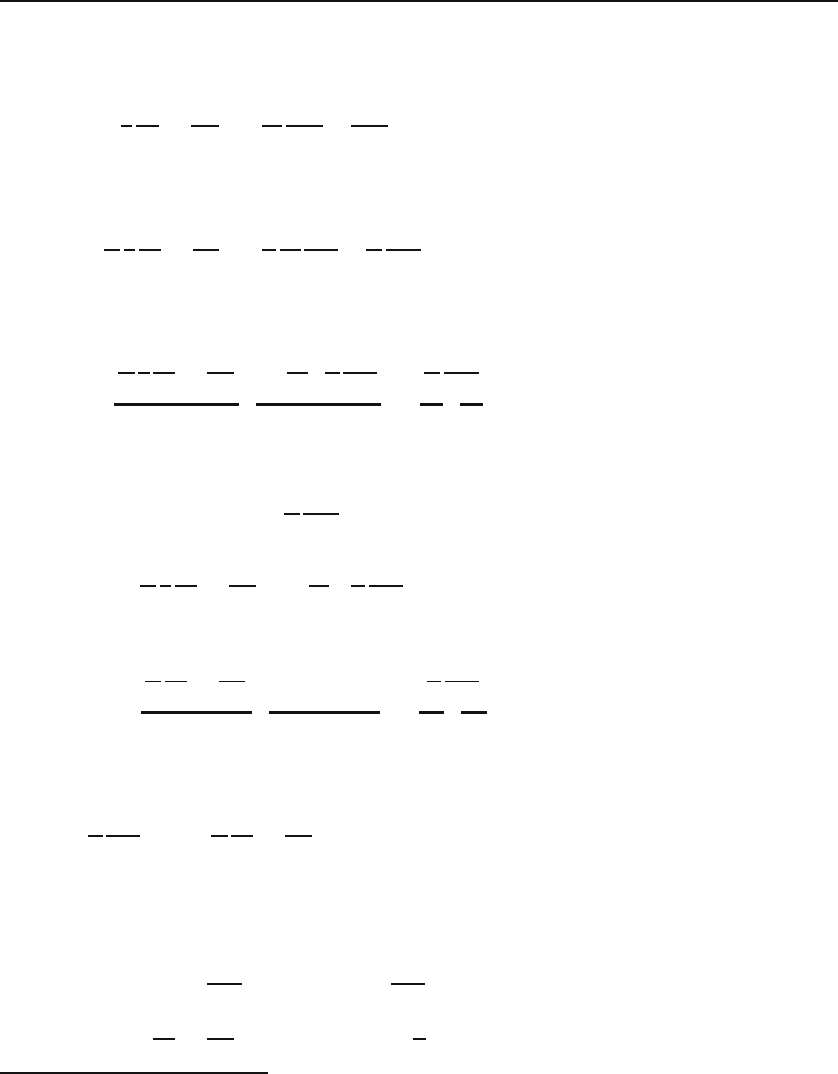
(a) In electrostatics, separation of Laplace’s equation, for which f(r) = 0, leads toLaplace’s equation
these ODEs:
d
2
X
dx
2
+ α
1
X =0,
d
2
Y
dy
2
+ α
2
Y =0,
d
2
Z
dz
2
− (α
1
+ α
2
)Z =0.
The solutions to these equations are trigonometric or hyperbolic (exponential) func-
tions, determined from the boundary conditions (conducting surfaces). The unsym-
metrical treatment of the three coordinates—the plus sign in front of the first two
constants and a minus sign in front of the third—is not dictated by the above equa-
tions. There is a freedom in the choice of sign in these equations. However, the
boundary conditions will force the constants to adapt to values appropriate to the
physical situation at hand.
(b) In quantum mechanics the time-independent Schr¨odinger equation for a free
particle in three dimensions is
∇
2
Ψ+
2mE
2
Ψ=0.
Separation of variables yields the ODEs of Equation (22.12) with
α
1
+ α
2
+ α
3
=
2mE
2
.
After time is separated, the heat and wave equations also yield equations similar to
(22.12).
(c) In quantum mechanics the time-independent Schr¨odinger equation for a three
dimensional isotropic harmonic oscillator is
∇
2
Ψ −
m
2
ω
2
2
r
2
−
2mE
2
Ψ=0.
Thus,
f(r)=−
m
2
ω
2
2
r
2
+
2mE
2
= −
m
2
ω
2
2
(x
2
+ y
2
+ z
2
)+
2mE
2
.
Equation (22.11) then yields
d
2
X
dx
2
−
m
2
ω
2
2
x
2
X + α
1
X =0,
d
2
Y
dy
2
−
m
2
ω
2
2
y
2
Y + α
2
Y =0,
d
2
Z
dz
2
−
m
2
ω
2
2
z
2
Z + α
3
Z =0,
with α
1
+ α
2
+ α
3
=2mE/
2
.
22.3 Separation in Cylindrical Coordinates 547
22.3 Separation in Cylindrical Coordinates
Equation (22.9) takes the following form in cylindrical coordinates:
4
1
ρ
∂
∂ρ
ρ
∂Ψ
∂ρ
+
1
ρ
2
∂
2
Ψ
∂ϕ
2
+
∂
2
Ψ
∂z
2
+ f (ρ, ϕ, z)Ψ = 0.
To separate the variables, we write Ψ(ρ, ϕ, z)=R(ρ)S(ϕ)Z(z), substitute in
the general equation, and divide both sides by RSZ to obtain
1
R
1
ρ
d
dρ
ρ
dR
dρ
+
1
S
1
ρ
2
d
2
S
dϕ
2
+
1
Z
d
2
Z
dz
2
+ f (ρ, ϕ, z)=0.
We shall consider only the special (but important) case in which f(ρ, ϕ, z)
is a constant λ. In that case, the equation becomes
1
R
1
ρ
d
dρ
ρ
dR
dρ
+
1
ρ
2
1
S
d
2
S
dϕ
2
function of ρ and ϕ only
+
1
Z
d
2
Z
dz
2
fn. of z
+λ =0.
The sum of the first two terms is independent of z, so the third term must be
as well. We thus get
1
Z
d
2
Z
dz
2
= λ
1
and
1
R
1
ρ
d
dρ
ρ
dR
dρ
+
1
ρ
2
1
S
d
2
S
dϕ
2
+ λ
1
+ λ =0.
Multiplying this equation by ρ
2
yields
ρ
R
d
dρ
ρ
dR
dρ
+(λ
1
+ λ)ρ
2
function of ρ only
+
1
S
d
2
S
dϕ
2
fn. of ϕ
=0.
Since the first term is a function of ρ only and the second a function of ϕ only,
both terms must be constants whose sum vanishes. Thus,
1
S
d
2
S
dϕ
2
= μ,
ρ
R
d
dρ
ρ
dR
dρ
+(λ
1
+ λ)ρ
2
+ μ =0. (22.13)
Putting together all of the above, we conclude that when Equation (22.9)
is separable in cylindrical coordinates and f (r)=λ, it will separate into the
following three ODEs:
d
2
Z
dz
2
− λ
1
Z =0,
d
2
S
dϕ
2
− μS =0,
d
dρ
ρ
dR
dρ
+
(
(λ
1
+ λ)ρ +
μ
ρ
)
R =0, (22.14)
4
See Chapter 16 for the expression of ∇
2
in spherical and cylindrical coordinate systems.

548 From PDEs to ODEs
where in rewriting the second equation in (22.13), we multiplied both sides of
the equation by R and divided it by ρ. The last equation of (22.14) is called the
Bessel differential equation. This equation shows up in electrostatic and
Bessel differential
equation
heat-transfer problems with cylindrical geometry and in problems involving
two-dimensional wave propagation, as in drumheads.
Historical Notes
Jean Le Rond d’Alembert was the illegitimate son of a famous salon host-
ess of eighteenth-century Paris and a cavalry officer. Abandoned by his mother,
d’Alembert was raised by a foster family and later educated by the arrangement of
his father at a nearby church-sponsored school, in which he received instruction in
the classics and above-average instruction in mathematics. After studying law and
medicine, he finally chose to pursue a career in mathematics. In the 1740s he joined
the ranks of the philosophes, a growing group of deistic and materialistic thinkers
and writers who actively questioned the social and intellectual standards of the day.
He traveled little (he left France only once, to visit the court of Frederick the Great),
preferring instead the company of his friends in the salons, among whom he was well
known for his wit and laughter.
Jean Le Rond
d’Alembert
1717–1783
d’Alembert turned his mathematical and philosophical talents to many of the
outstanding scientific problems of the day, with mixed success. Perhaps his most
famous scientific work, entitled Traite de dynamique, shows his appreciation that
a revolution was taking place in the science of mechanics—the formalization of
the principles stated by Newton into a rigorous mathematical framework. Later,
d’Alembert produced a treatise on fluid mechanics, a paper dealing with vibrating
strings, and a skillful treatment of celestial mechanics. d’Alembert is also credited
with the use of the first partial differential equation as well as the first solution to
such an equation using separation of variables.
Much of the work for which d’Alembert is remembered occurred outside math-
ematical physics. He was chosen as the science editor of the Encyclopedie, and his
lengthy Discours Preliminaire in that volume is considered one of the defining doc-
uments of the Enlightenment. Other works included writings on law, religion, and
music.
22.4 Separation in Spherical Coordinates
By far the most commonly used coordinate system in mathematical physics
is the spherical coordinate system. This is because forces, potential energies,
and most geometries encountered in Nature have a spherical symmetry. One
of the consequences of this spherical symmetry is that the function f (r)is
a function of r and not of angles. We shall assume this to be true in this
subsection.
In spherical coordinates, Equation (22.9) becomes [see Equation (16.19)]
1
r
2
∂
∂r
r
2
∂Ψ
∂r
+
1
r
2
sin θ
(
∂
∂θ
sin θ
∂Ψ
∂θ
+
1
sin θ
∂
2
Ψ
∂ϕ
2
)
+f(r)Ψ=0. (22.15)
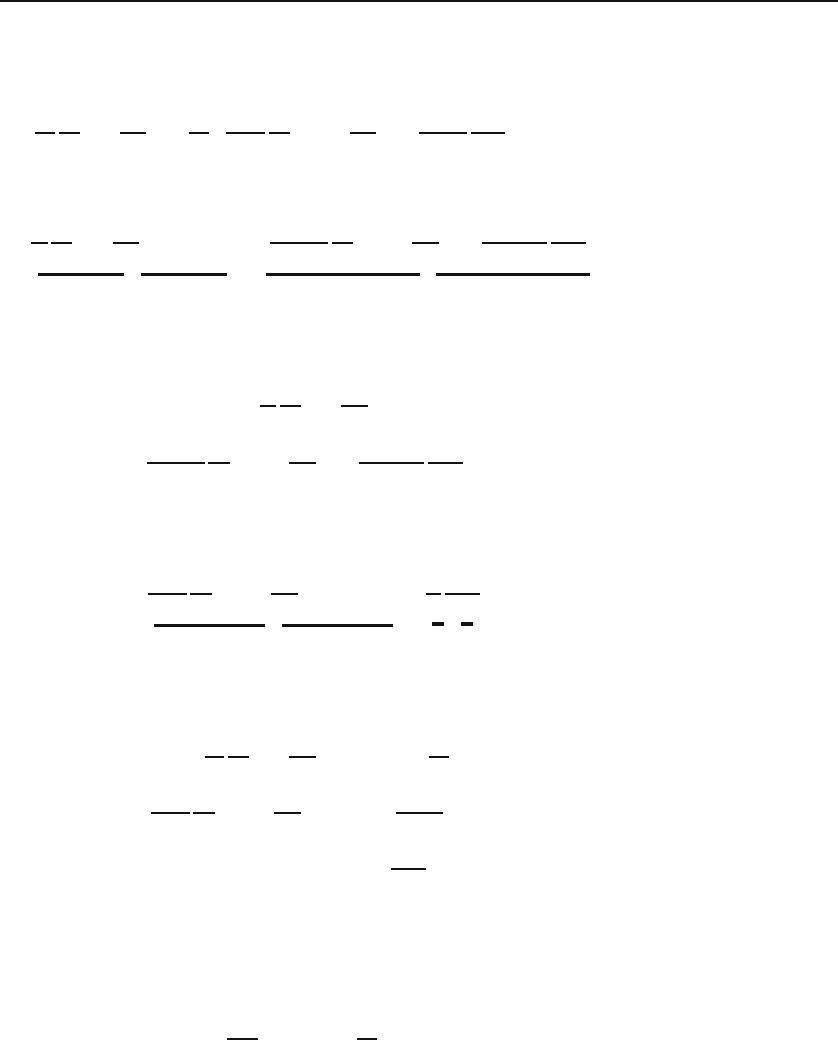
22.4 Separation in Spherical Coordinates 549
To separate this equation means to write Ψ(r, θ, ϕ)=R(r)Θ(θ)Φ(ϕ). If we
substitute this in Equation (22.15) and note that each differentiation acts on
only one of the three functions, we get
ΘΦ
1
r
2
d
dr
r
2
dR
dr
+
R
r
2
Φ
sin θ
d
dθ
sin θ
dΘ
dθ
+
Θ
sin
2
θ
d
2
Φ
dϕ
2
+ f (r)RΘΦ = 0.
Now divide both sides by RΘΦ and multiply by r
2
to obtain
1
R
d
dr
r
2
dR
dr
+ r
2
f(r)
function of r alone
+
1
Θsinθ
d
dθ
sin θ
dΘ
dθ
+
1
Φsin
2
θ
d
2
Φ
dϕ
2
function of θ and ϕ only
=0.
Since each one of the two terms is a function of different variables, each must
be a constant; and the two constants must add up to zero. Therefore, we have
1
R
d
dr
r
2
dR
dr
+ r
2
f(r)=α,
1
Θsinθ
d
dθ
sin θ
dΘ
dθ
+
1
Φsin
2
θ
d
2
Φ
dϕ
2
= −α.
The second equation can be further separated. We add α to both sides and
multiply the resulting equation by sin
2
θ to obtain
sin θ
Θ
d
dθ
sin θ
dΘ
dθ
+ α sin
2
θ
function of θ alone; set = β
+
1
Φ
d
2
Φ
dϕ
2
=−β
=0.
We have thus obtained three ODEs in three variables. We rewrite these ODEs
in the following equations:
1
r
2
d
dr
r
2
dR
dr
+
*
f(r) −
α
r
2
+
R =0,
1
sin θ
d
dθ
sin θ
dΘ
dθ
+
α −
β
sin
2
θ
Θ=0, (22.16)
d
2
Φ
dϕ
2
+ βΦ=0.
radial, polar, and
azimuthal
equations
The first equation is called the radial equation, the second the polar
equation, and the third the azimuthal equation. The radial equation can
be further simplified by making the substitution R = u/r.Thisgives
d
2
u
dr
2
+
*
f(r) −
α
r
2
+
u =0. (22.17)
Our task in this chapter was to separate the PDEs most frequently encoun-
tered in undergraduate mathematical physics into ODEs; and we have done

550 From PDEs to ODEs
this in the three coordinate systems regularly used in applications. We shall
return to a thorough treatment of the ODEs so obtained later in the book,
and in the process we shall be introduced to the so-called special functions
that came into being in the nineteenth century as a result of the then newly
discovered technique of the separation of variables.
22.5 Problems
22.1. Assume that two functions Φ
1
and Φ
2
satisfy the Poisson equation.
Show that
(a) Φ defined by Φ = Φ
1
− Φ
2
satisfies the Laplace’s equation;
(b) ∇ ·(Φ∇Φ) = |∇Φ|
2
22.2. Separate the solution of the heat equation (22.3): T (r,t) ≡ R(r)τ(t),
and show that
(a) the solution to the time equation is
τ(t)=Ae
−αk
2
t
,
(b) in which case, the space part must satisfy the following PDE:
∇
2
R + αR =0
22.3. Show that any function of the form f (k · r ± ωt) satisfies the wave
equation (22.4) if ω = c|k|.
22.4. Separate the solution of the wave equation (22.4): Ψ(r,t) ≡ R(r)T (t),
and show that
(a) the solution to the time equation is
T (t)=A cos ωt + B sin ωt,
(b) and the space part must satisfy the following PDE:
∇
2
R + k
2
R =0
where k = ω/c.
22.5. Provide the details of the derivation of Equation (22.16).
22.6. By substituting R = u/r in the radial DE of spherical coordinates,
show that it reduces to Equation (22.17).

Chapter 23
First-Order Differential
Equations
The last chapter showed that all PDEs discussed there resulted in ODEs of
second order, i.e., differential equations involving second derivatives. Thus,
treating the first-order DEs (FODEs) may seem irrelevant. However, some-
times a second-order DE (SODE) may be expressed in terms of first deriva-
tives. For example, take Newton’s second law of motion along a straight
line (free fall, say): md
2
x/dt
2
= F . If we write this in terms of velocity,
we obtain mdv/dt = F ,andifF is a function of v alone—as in a fall with
air resistance—then we have a FODE. FODEs arise in other areas of physics
beside mechanics. Therefore, it is worthwhile to study them here.
23.1 Normal Form of a FODE
The most general FODE is of the form G(x, y, y
)=0,whereG is some
function of three variables. We can find y
(the derivative of y) as a function
of x and y if the function G(x
1
,x
2
,x
3
) is sufficiently well behaved. In that
case, we have
the most general
FODE in normal
form
y
≡
dy
dx
= F (x, y) (23.1)
whichissaidtobeanormal FODE.
Example 23.1.1.
There are three special cases of Equation (23.1) that lead im-
mediately to a solution.
(a) If F (x, y) is independent of y,theny
= g(x), and the most general solution can
be written as y = f(x)=C +
x
a
g(t) dt where C = f(a).
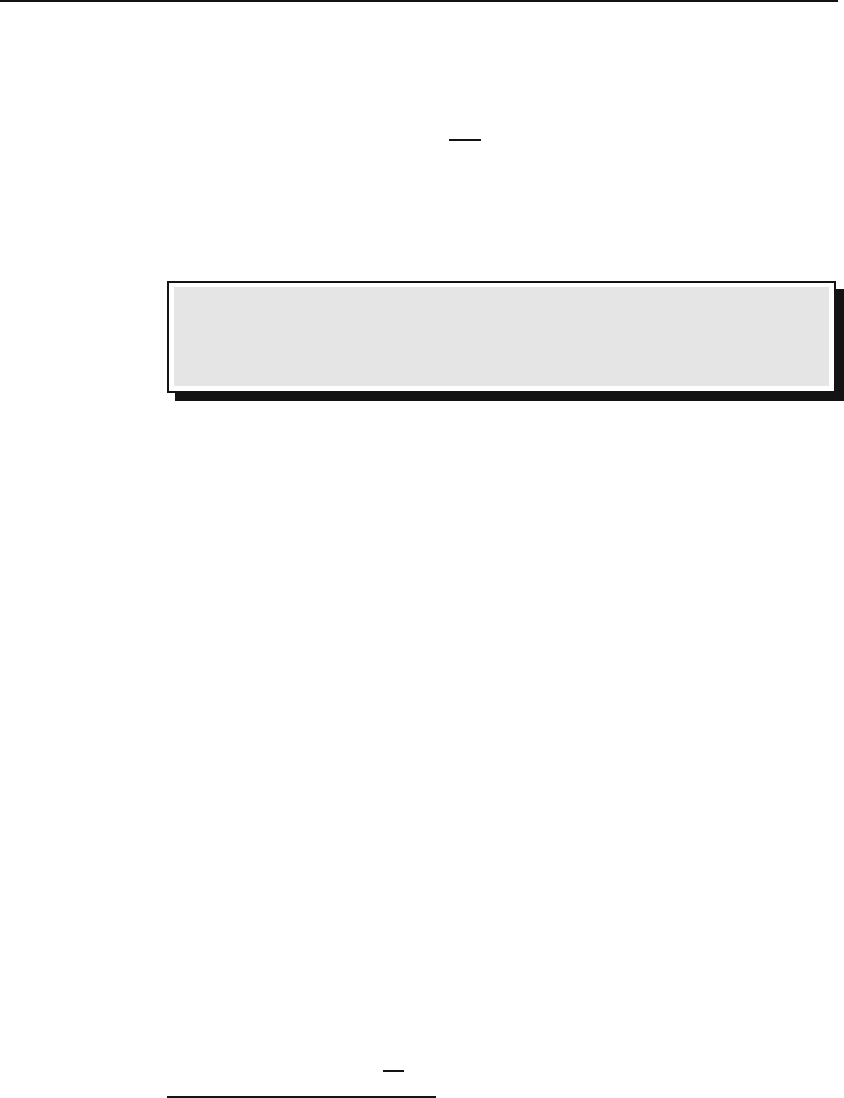
(b) If F (x, y) is independent of x,thendy/dx = h(y), and
dy
h(y)
= dx ⇒
#
y
C
dt
h(t)
≡H(y)
−x + a =0 ⇒ H(y) − x + a =0
552 First-Order Differential Equations
embodies a solution. That is, H(y)=x − a canbesolvedfory in terms of x,say
y = f(x), and this y will be a solution of the DE. Note that y|
x=a
≡ f(a)=C.
(c) The third special case is really a generalization of the first two. If F (x, y)=
g(x)h(y), then y
= g(x)h(y)ordy/h(y)=g(x) dx and
#
y
C
dt
h(t)
=
#
x
a
g(t) dt (23.2)
is an implicit solution.
The example above contains an information which is important enough to
be “boxed.”
Box 23.1.1. A differential equation is considered to be solved if its solu-
tion can be obtained by solving an algebraic equation involving integrals of
known functions. Whether these integrals can be done in closed form or
not is irrelevant.
So, although we may not be able to actually perform the integration of (23.2),
we consider the DE solved because, in principle, Equation (23.2) gives y as a
(implicit) function of x.
As Example 23.1.1 shows, the solutions to a FODE are usually obtained
in an implicit form, as a function u of two variables such that the solution y
can be found by solving u(x, y)=0fory. Included in u(x, y) is an arbitrary
constant related to the initial conditions. The equation u(x, y) = 0 defines
acurveinthexy-plane, which depends on the (hidden) constant in u(x, y).
Since different constants give rise to different curves, it is convenient to sep-
arate the constant and write u(x, y)=C. This leads to the concept of an
integral of a differential equation.
integral of a
normal FODE
Definition 23.1.1. An integral of a normal FODE [Equation (23.1)] is
a function of two variables u(x, y) such that u(x, f (x)) is a constant for all
possible values of x whenever y = f (x) is a solution of the differential equation.
The integrals of differential equations are encountered often in physics. If
an integral of a
FODE is also
called a constant
of motion.
x is replaced by t (time), then the differential equation describes the motion
of a physical system, and a solution, y = f(t), can be written implicitly as
u(t, y)=C,whereu is an integral of the differential equation. The equation
u(t, y)=C describes a curve in the ty-plane on which the value of the function
u(t, y) remains unchanged for all t.Thus,u(t, y), the integral of the FODE,
is also called a constant of motion.
Example 23.1.2.
Consider a point particle moving under the influence of a force
depending on position only. Denoting the position
1
by x and the velocity by v,
we have, by Newton’s second law, mdv/dt = F (x). Using the chain rule, dv/dt =
(dv/dx)(dx/dt)=vdv/dx,weobtain
mv
dv
dx
= F (x) ⇒ mv dv = F (x) dx, (23.3)
1
Here we are restricting the motion to one dimension.

23.2 Integrating Factors 553
which is easily integrated to
1
2
mv
2
=
#
F (x) dx + C ≡−V (x)+C. (23.4)
The potential energy V (x)=−
F (x) dx has been introduced as an indefinite potential energy
integral. We can write Equation (23.4) as
1
2
mv
2
+ V (x)=C. (23.5)
Thus, the integral of Equation (23.3) is u(x, v)=
1
2
mv
2
+ V (x)whichistheex-
pression for the energy of the one-dimensional motion of a particle experiencing the
potential V (x). If v is a solution of Equation (23.3), then u(x, v) = constant. Since
a solution of Equation (23.3) describes a possible motion of the particle, Equation
(23.5) implies that the energy of a particle does not change in the course of its
motion. This statement is the conservation of (mechanical) energy.
23.2 Integrating Factors
Let D bearegioninthexy-plane, and let M(x, y)andN (x, y) be continuous
functions of x and y defined on D. The differential Mdx+ Ndy is exact if,
for arbitrary points P
1
and P
2
of D, the line integral exact differential
#
P
2
P
1
[M(x, y) dx + N(x, y) dy]
is independent of the path joining the two points. This condition is equivalent
to saying that the line integral of the integrand around any closed loop in
D vanishes. A necessary and sufficient condition for exactness is, therefore,
that the curl of the vector A = M, N, 0 be zero.
2
The vector A is then
conservative, and we can define a (potential) function v such that A = ∇v =
∂v/∂x,∂v/∂y,0,or
dv =
∂v
∂x
dx +
∂v
∂y
dy = Mdx+ Ndy. (23.6)
Thus, Mdx+ Ndy is exact if and only if there exists a function v(x, y)
satisfying (23.6), in which case, M = ∂v/∂x and N = ∂v/∂y.
Now consider all y’s that satisfy v(x, y)=C for some constant C.Then
since dC =0,wehave
0=dv = Mdx+ Ndy.
It follows that v(x, y)=C is an implicit solution of the differential equation.
We therefore have
2
The statement is true only if the region D does not contain any singularities of M or
N. The region is then called contractable to a point (see Section 14.3).
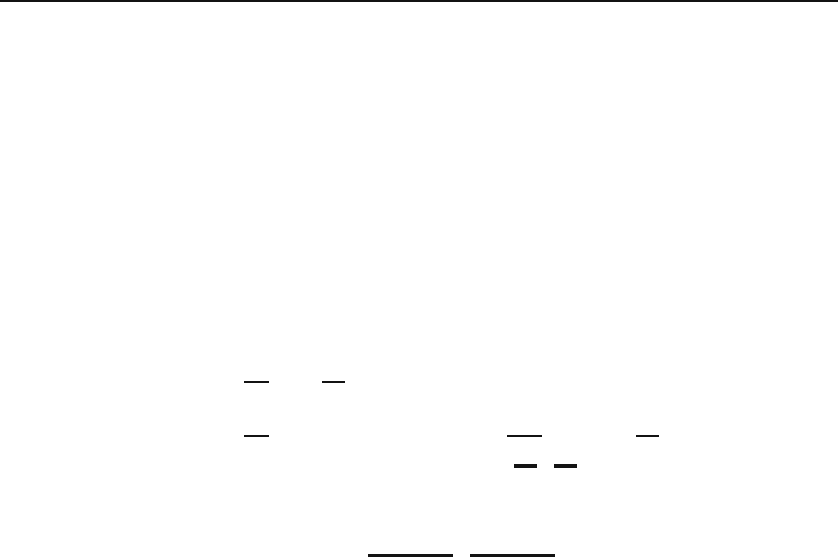
554 First-Order Differential Equations
Theorem 23.2.1. If M(x, y) dx + N(x, y) dy is an exact differential dv in a
domain D of the xy-plane, then v(x, y) is an integral of the DE
M(x, y) dx + N(x, y) dy =0
whose solutions are of the form v(x, y)=C.
We saw above that, for an exact differential, M = ∂v/∂x and N = ∂v/∂y.
A necessary consequence of this result is ∂M/∂y = ∂N/∂x. Could this relation
be a sufficient condition as well? Consider the function v(x, y) defined by
v(x, y) ≡
#
x
a
M(t, y) dt +
#
y
b
N(a, t) dt,
and note that
dv =
∂v
∂x
dx +
∂v
∂y
dy
=
∂
∂x
#
x
a
M(t, y) dt
dx +
#
x
a
∂M
∂y
(t, y)
∂N/∂t
dt +
∂
∂y
#
y
b
N(a, t) dt
dy
= M(x, y) dx +
N(t, y)
t=x
t=a
+ N (a, y)
=N(x,y)
dy,
and v(x, y) indeed satisfies dv = Mdx+ Ndy. It follows that (see Problem
23.1)
Theorem 23.2.2. A necessary and sufficient condition for Mdx+ Ndy to
be exact is ∂M/∂y = ∂N/∂x,inwhichcase
v(x, y) ≡
#
x
a
M(t, y) dt +
#
y
b
N(a, t) dt
is the function such that dv = Mdx+ Ndy.
Not very many FODEs are exact. However, there are many that can be
turned into exact FODEs by multiplication by a suitable function. Such a
function, if it exists, is called an integrating factor. Thus, if the differential
integrating factor
M(x, y) dx + N(x, y) dy is not exact, but
μ(x, y)M(x, y) dx + μ(x, y)N(x, y) dy = dv,
then μ(x, y) is an integrating factor for the differential equation
M(x, y) dx + N(x, y) dy =0
whose solution is then v(x, y)=C. Integrating factors are not unique, as the
following example illustrates.
23.2 Integrating Factors 555
Example 23.2.3. The differential xdy− ydx is not exact. Let us see if we can illustration of
nonuniqueness of
integrating factor
find a function μ(x, y) such that dv = μx dy − μy dx,forsomev(x, y). We assume
that the domain D of the xy-plane in which v is defined is contractable to a point.
Then a necessary and sufficient condition for the equation above to hold is
∂
∂x
(μx)=
∂
∂y
(−μy) ⇒ x
∂μ
∂x
+ y
∂μ
∂y
+2μ =0. (23.7)
(a) Let us assume that μ is a function of x only. Then Equation (23.7) reduces to
xdμ/dx=2μ or μ = C/x
2
where x =0. Inthiscaseweget
dv = C
1
x
dy −
y
x
2
dx
= Cd
y
x
where x =0.
Thus, as long as x = 0, any function C/x
2
, with arbitrary C,isanintegratingfactor
for xdy− ydx= 0. This integrating factor leads to the solution
v =
Cy
x
= constant. (23.8)
In order to determine the constant, suppose that y = m when x = 1. Then (23.8)
determines the constant in terms of m:
Cm
1
= constant ⇒ constant = Cm.
So, (23.8) becomes
Cy
x
= Cm ⇒ y = mx.
(b) Now let us assume that μ is a function of y only. This leads to the integrating
factor μ = C/y
2
where y =0. Inthiscasev = Cx/y is the integral of the DE, and a
general solution is of the form Cx/y = constant. If we further impose the condition
y(1) = m,wegetC/m = constant. Equation (23.8) then yields
Cx
y
=
C
m
⇒ y = mx
as in (a).
(c) The reader may verify that
μ =
C
x
2
+ y
2
where (x, y) =(0, 0)
is also an integrating factor leading to the integral
v =tan
−1
y
x
= constant ⇒
y
x
= tan(constant) ≡ C
.
Imposing y(1) = m gives C
= m,sothaty = mx as before.
The example above is a special case of the general fact that if a differential
has one integrating factor, then it has an infinite number of them. Suppose
proof of
nonuniqueness of
integrating factor
that ν(x, y) is an integrating factor of Mdx+ Ndy, i.e., νM dx + νN dy is
an exact differential, say du.Takeany differentiable function F (u). Then
μ(x, y) ≡ ν(x, y)F
(u) is also an integrating factor. In fact,
μ(Mdx+ Ndy)=νF
(Mdx+ Ndy)=
dF
du
(νM dx + νN dy)
=du
= dF.
