Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

534 Calculus of Residues

Figure 21.3: To avoid the origin move on an inﬁnitesimal semicircle γ



of radius .

circle of radius  as shown in Figure 21.3. This contour does not surround a pole.

Therefore, we can write

iaz

dz =

−

−∞

iax

dx +



iaz

dz +

∞



iax

As  → 0, the two integrals in x become a single integral over all real numbers.

Thus, we get

∞

−∞

iax

dx = − lim

→0



iaz

But on γ



, z = e

iθ

.Thus

lim

→0



iaz

dz = lim

→0

iae

iθ

e

iθ

ie

iθ

dθ = i lim

→0

iae

iθ

dθ = −iπ

and

∞

−∞

iax

dx = iπ.

Putting everything together, we obtain

∞

sin ax

dx =

∞

−∞

sin ax

dx =

∞

−∞

iax

dx =

Im(iπ)=

If a<0, then sin ax = −sin |a|x and we get the negative of the answer above. 

21.4 Functions of Trigonometric Functions

The third type of integral we can evaluate using the residue theorem involves

only trigonometric functions and is typically of the form

2π

F (sin θ, cos θ) dθ,

where F is some (typically rational) function

of its arguments. Since θ varies

from0to2π, we can consider it as the angle of a point z on the unit circle

Recall that a rational function is, by deﬁnition, the ratio of two polynomials.

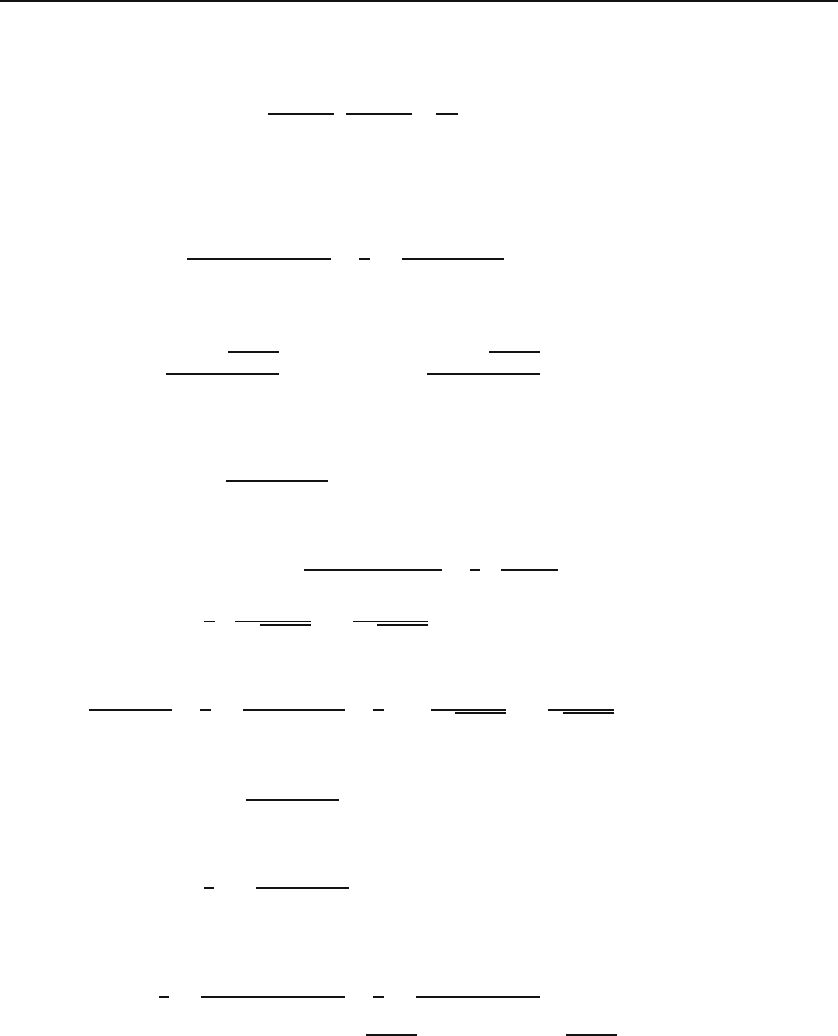
21.4 Functions of Trigonometric Functions 535

centered at the origin. Then z = e

iθ

and e

−iθ

=1/z, and we can substitute

cos θ =(z +1/z)/2, sin θ =(z − 1/z)/(2i), and dθ = dz/(iz) in the original

integral to obtain



z − 1/z

z +1/z



This integral can often be evaluated using the method of residues.

Example 21.4.1.

Let us evaluate the integral



2π

dθ/(1 + a cos θ)where|a| < 1.

Substituting for cos θ and dθ in terms of z,weobtain

dz/iz

1+a[(z

+1)/2z]

2z + az

+ a

where C is the unit circle centered at the origin. The singularities of the integrand

are the zeros of its denominator 2z + az

+ a ≡ a(z −z

)(z −z

)with

−1+

√

1 − a

and z

−1 −

√

1 − a

For |a| < 1 it is clear that z

will lie outside the unit circle C; therefore, it does not

contribute to the integral. But z

lies inside, and we obtain

2z + az

+ a

=2πiRes[f(z

)].

The residue of the simple pole at z

can be calculated:

Res[f(z

)] = lim

z→z

(z −z

)

a(z − z

)(z − z

)



− z





√

1 − a



√

1 − a

It follows that

2π

dθ

1+a cos θ

2z + az

+ a

2πi



√

1 − a



2π

√

1 − a



Example 21.4.2. As another example, let us consider the integral

I =

dθ

(a +cosθ)

where a>1.

Since cos θ is an even function of θ,wemaywrite

I =

−π

dθ

(a +cosθ)

where a>1.

This integration is over a complete cycle around the origin, and we can make the

usual substitution:

I =

dz/iz

[a +(z

+1)/2z]

zdz

+2az +1)

The denominator has the roots z

= −a +

√

− 1andz

= −a −

√

− 1which

are both of order 2. The second root is outside the unit circle because a>1. The

reader may verify that for all a>1, z

is inside the unit circle. Since z

is a pole of

order 2, we have

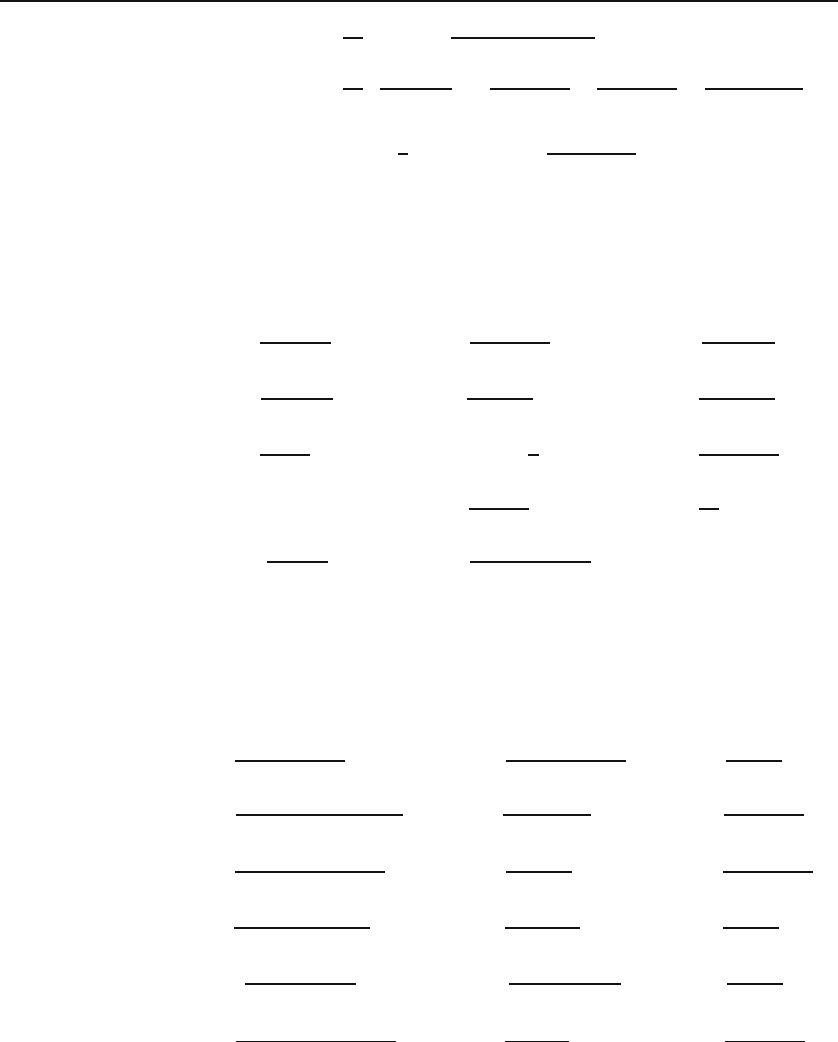
536 Calculus of Residues

Res[f(z

)] = lim

z→z



(z − z

)

(z − z

)

(z −z

)



= lim

z→z



(z − z

)



− z

)

−

− z

)

4(a

− 1)

3/2

We thus obtain

I =

2πiRes[f(z

)] =

πa

− 1)

3/2



21.5 Problems

21.1. Evaluate each of the following integrals, for all of which C is the circle

|z| =3:

(a)

4z − 3

z(z − 2)

dz. (b)

z(z − iπ)

dz. (c)

cos z

z(z − π)

dz.

(d)

z(z − 1)

dz. (e)

cosh z

+ π

dz. (f)

1 − cos z

dz.

(g)

sinh z

dz. (h)

z cos





dz. (i)

(z +5)

dz.

(j)

tan zdz. (k)

sinh 2z

dz. (l)

dz.

(m)

sin z

dz. (n)

(z − 1)(z −2)

21.2. Find the residue of f(z)=1/ cos z at all its poles.

21.3. Evaluate the integral



∞

dx/[(x

+1)(x

+ 4)] by closing the contour

(a) in the UHP and (b) in the LHP.

21.4. Evaluate the following integrals in which a and b are nonzero real con-

stants:

(a)

∞

+5x

dx. (b)

∞

+5x

. (c)

∞

(d)

∞

cos xdx

+ a

)

+ b

)

. (e)

∞

cos ax

+ b

)

dx. (f)

∞

+1)

(g)

∞

+1)

+2)

. (h)

∞

− 1

dx. (i)

∞

+ a

)

(j)

∞

−∞

xdx

+4x + 13)

. (k)

∞

sin ax

dx. (l)

∞

dx.

(m)

∞

−∞

x cos xdx

− 2x +10

. (n)

∞

−∞

x sin xdx

− 2x +10

. (o)

∞

(p)

∞

+4)

+ 25)

. (q)

∞

cos ax

+ b

dx. (r)

∞

+4)

21.5. Evaluate each of the following integrals by turning them into contour

integrals around the unit circle.

21.5 Problems 537

(a)

2π

dθ

5+4sinθ

. (b)

2π

dθ

a +cosθ

where a>1.

(c)

2π

dθ

1+sin

. (d)

2π

dθ

(a + b cos

θ)

where a, b > 0.

(e)

2π

cos

3θ

5 − 4cos2θ

dθ. (f)

dφ

1 − 2a cos φ + a

where a = ±1.

(g)

cos

3φdφ

1 − 2a cos φ + a

where a = ±1.

(h)

cos 2φdφ

1 − 2a cos φ + a

where a = ±1.

21.6. Use the method of residues to show that

cos

θdθ= π

(2n)!

(n!)

21.7. Use the contour in Figure 21.4(a) to show that

∞

−∞

sin x

dx = π

by letting X →∞, Y →∞,and → 0.

21.8. Use the contour in Figure 21.4(b) to show that

∞

1+x

dx =

π/n

sin(π/n)

by letting R →∞.

21.9. Use the contour in Figure 21.4(c) to show that

∞

sin(x

) dx =

∞

cos(x

) dx =



by letting R →∞.

−X −ε ε

+ iY−X

+ iY

2π /n

(a) (c)(b)

Figure 21.4: (a) The contour used for sin x/x. (b) The contour used for 1/(1 + x

Part VI

Diﬀerential Equations

Chapter 22

From PDEs to ODEs

Physics, as the most exact science, is characterized by its ability to make

mathematical predictions. Predictions are based on two factors: the initial

information (data), and the law governing the physical process. Knowing

what the situation is here and now (initial data, initial conditions, boundary

conditions) enables physics to predict what the situation will be there and

then. This ability to predict is based on the intuitive belief that physical

quantities, dependent on continuous parameters such as position and time,

must be continuous functions of those parameters. Thus, knowledge of the

initial conditions

are needed to

predict the

evolution of a

physical system.

values of those functions at one (initial) point and of how the functions change

from one point to a neighboring point (given by the laws of physics) allows

the values of the functions at the neighboring point to be predicted. Once

the values of the functions are determined at the new point, their values can

be predicted for its neighboring points, and the process can continue until a

distant point is reached.

In mechanics, for example, knowledge of the force acting on a particle of

mass m, located at r

and moving with momentum p

at time t

, allows its

momentum and position at a later time t

+Δt to be predicted as follows.

Because dp/dt = F by Newton’s second law of motion, we have

Δp ≈ F(r

, p

)Δt

and

p(t

+Δt)=p

+Δp ≈ p

+ F(r

, p

)Δt.

Similarly,

r(t

+Δt) ≈ r

+ v

t ≈ r

Δt.

The smaller Δt is, the better the prediction will be.

Newton’s second law of motion,





= F(r,dr/dt, t)

542 From PDEs to ODEs

is an example of an ordinary diﬀerential equation (ODE). A dependentordinary

diﬀerential

equation (ODE)

variable r is determined from an equation involving a single independent vari-

able t, the dependent variable r, and its various derivatives.

In (point) particle mechanics there is only one independent variable, lead-

ing to ODEs. In other areas of physics, however, in which extended objects

such as ﬁelds are studied, variations with respect to position are also present.

Partial derivatives with respect to coordinate variables show up in the diﬀer-

ential equations, which are therefore called partial diﬀerential equations

partial diﬀerential

equations (PDEs)

(PDEs). For instance, in electrostatics, where time-independent scalar ﬁelds

such as potentials, and vector ﬁelds such as electrostatic ﬁelds, are studied,

the law is described by Poisson’s equation, ∇

Φ(r)=−4πρ(r), where Φ is

the electrostatic potential and ρ is the volume charge density. Other PDEs

occurring in mathematical physics include the heat equation, describing the

transfer of heat, the wave equation, describing the propagation of various

kinds of wave, and the Schr¨odinger equation, describing nonrelativistic quan-

tum mechanical phenomena.

In fact, except for the laws of particle mechanics and electrical circuits,

in which the only independent variable is time, almost all laws of physics are

described by PDEs. We shall not study PDEs in their full generalities, but

concentrate on the simplest ones encountered most frequently in ideal physical

applications. The method of solution that works for all these equations is the

separation of variables,wherebyaPDEisturnedintoanumberofODEs.

Before embarking on the separation of variables, we need to formalize the

discussion above. An ordinary or a partial DE will provide a unique solution

to a physical problem only if the initial or the starting value of the solution

is known. We refer to this as the boundary conditions,orBCsforshort.

the meaning of

boundary

conditions (or

BCs) elaborated

For ODEs, boundary conditions amount to the speciﬁcation of one or more

properties of the solution at an initial time; that is why for ODEs, one speaks

of initial conditions. BCs for PDEs involve speciﬁcation of the solution on

a surface (or a curve, if the PDE has only two variables).

22.1 Separation of Variables

We list here the PDEs encountered in undergraduate courses and initiate

their transformation into ODEs. Let us start with the simplest PDE arising

in electrostatic problems, the Poisson equation, derived in Chapter 15,

Poisson equation

Laplace’s equation

∇

Φ(r)=−4πρ(r). (22.1)

In vacuum, where ρ(r) = 0, Equation (22.1) reduces to Laplace’s equation,

∇

Φ(r)=0. (22.2)

Many electrostatic problems involve conductors held at constant potentials

and situated in a vacuum. In the space between such conducting surfaces, the

electrostatic potential obeys Equation (22.2).

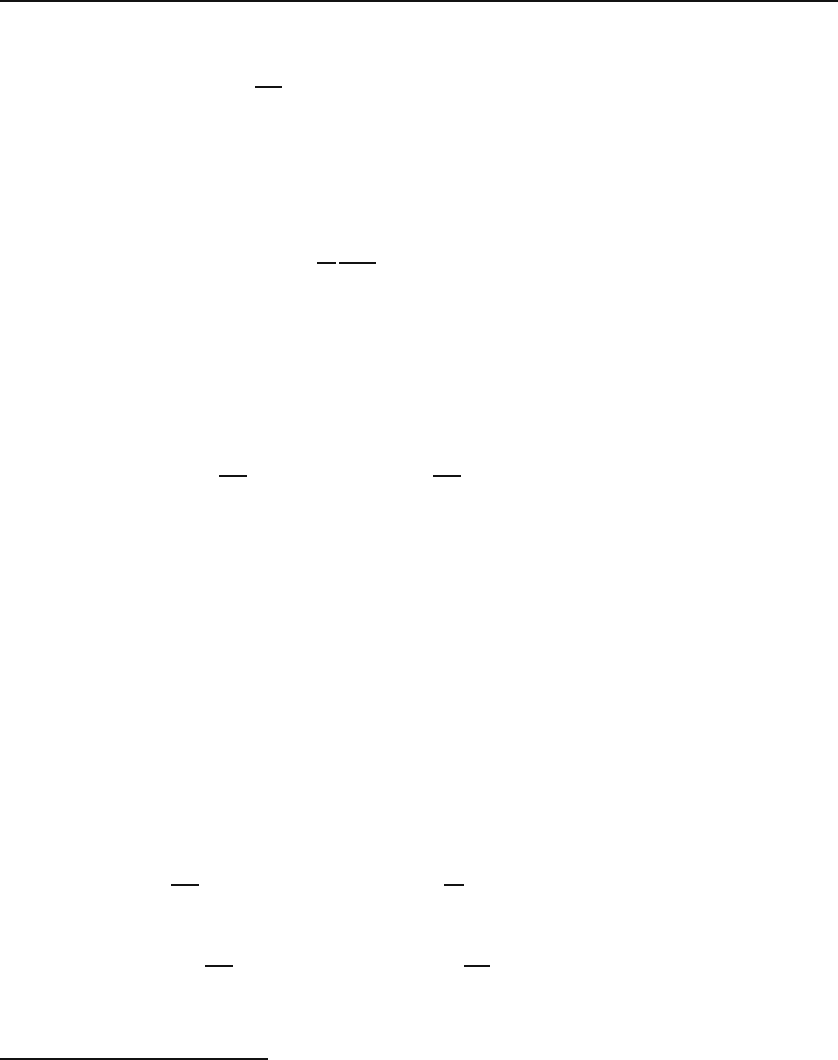
22.1 Separation of Variables 543

Next in complexity is the heat equation, whose most simpliﬁed version— heat equation

the one studied here—is

∂T

∂t

= k

∇

T (r,t), (22.3)

where T is the temperature and k is a real constant characterizing the medium

in which heat is ﬂowing.

Probably one of the most recurring PDEs encountered in mathematical

physicsisthewave equation,

wave equation

∇

Ψ −

∂

∂t

=0. (22.4)

This equation (or its simpliﬁcation to lower dimensions) is applied to the

vibration of strings and drums, the propagation of sound in gases, solids, and

liquids, the propagation of disturbances in plasmas, and the propagation of

electromagnetic waves.

The Schr¨odinger equation, describing the nonrelativistic quantum phe-

Schr¨odinger

equation

nomena, is

−



∇

Ψ+V (r)Ψ = −i

∂Ψ

∂t

, (22.5)

where m is the mass of a subatomic particle,  is Planck’s constant (divided by

2π), V is the potential energy of the particle, and |Ψ(r,t)|

is the probability

density of ﬁnding the particle at r at time t.

Equations (22.3)–(22.5) have partial derivatives with respect to time. As

a ﬁrst step toward solving these PDEs, let us separate the time variable. We

will denote the functions in all four equations by the generic symbol Ψ(r,t).

The separation of variables starts with separating the r and t dependence

into factors:

Ψ(r,t) ≡ R(r)T (t).

This factorization permits us to separate the two operations of space diﬀer-

time is separated

from space

entiation and time diﬀerentiation. As an illustration, we separate the time

and space dependence for the Schr¨odinger equation. The other equations are

done similarly. Substituting for Ψ, we get

−



∇

(RT )+V (r)(RT )=−i

∂

∂t

(RT ),

−T



∇

R + V (r)(RT)=−iR

where we have used ordinary derivatives for T because, by assumption, it is

a function of a single variable. Dividing both sides by RT yields

Note that there is no a priori reason why the basic assumption underlying the separation

of variables is legitimate. After all, we cannot write sin(xt) as a product, f(x)g(t). However,

in all cases of physical interest the separation of variables works.

544 From PDEs to ODEs

−



∇

R + V (r)=−i



. (22.6)

Now comes the crucial step in the process of the separation of variables.

central argument

in separation of

variables

The LHS of Equation (22.6) is a function of position alone,andtheRHSisa

function of time alone.Sincer and t are independent variables, the only way

that (22.6) can hold is for both sides to be constant,sayα:

−



∇

R + V (r)=α ⇒−



∇

R + V (r)R = αR

and

−i

= α ⇒

iα



T. (22.7)

We have reduced the original time-dependent Schr¨odinger equation, a

PDE, to an ODE involving only time, and a PDE involving only the posi-

tion variables. Most problems of elementary mathematical physics have the

same property, i.e., they are completely equivalent to Equation (22.7) plus

the equation before it, which we write generically as

∇

R + f(r)R =0, (22.8)

where we have simpliﬁed the notation by including α in the function f .

The foregoing discussion is summarized in this statement:

Box 22.1.1. The time-dependent PDEs of mathematical physics can be

reduced to an ODE in the time variable and the PDE given in Equation

(22.8). For those PDEs involving second time derivatives, such as the

wave equation, (22.7) will be a second-order ODE.

With the exception of Poisson’s equation, in all the foregoing equations

the term on the RHS is zero. We will restrict ourselves to this so-called

homogeneous case

and rewrite (22.8) as

∇

Ψ(r)+f(r)Ψ(r)=0. (22.9)

The rest of this section is devoted to the study of this equation in various

coordinate systems.

22.2 Separation in Cartesian Coordinates

In Cartesian coordinates, Equation (22.9) becomes

∂

∂x

∂

∂y

∂

∂z

+ f (x, y, z)Ψ=0.

The most elegant way of solving inhomogeneous PDEs is the method of Green’s func-

tions, of which we shall have a brief discussion in Chapter 29. For a thorough discussion

of Green’s functions, see Hassani, S. Mathematical Physics: A Modern Introduction to Its

Foundations, Springer-Verlag, 1999, Part VI.

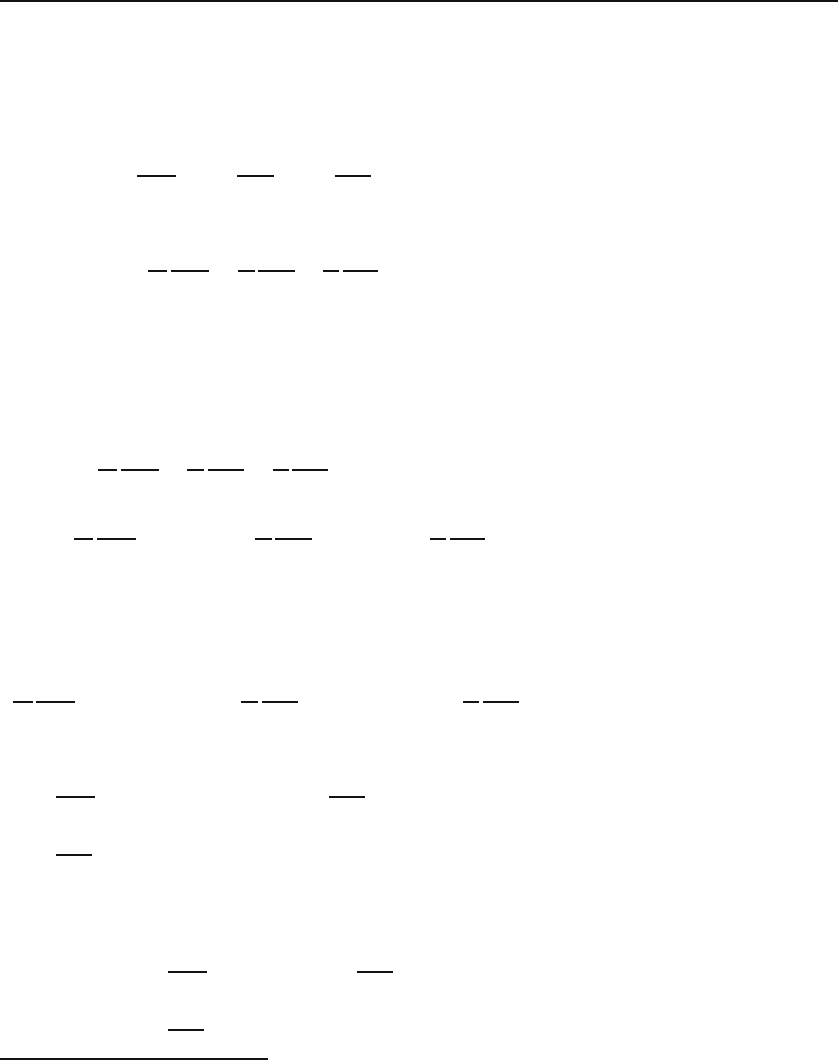
22.2 Separation in Cartesian Coordinates 545

As in the case of the separation of the time variable, we assume that we can

separate the dependence on various coordinates and write

Ψ(x, y, z)=X(x)Y (y)Z(z).

Then the above PDE yields

+ XZ

+ XY

+ f (x, y, z)XYZ =0.

Dividing by XYZ gives

+ f (x, y, z)=0. (22.10)

This equation is almost separated. The ﬁrst term is a function of x alone, the

second of y alone, and the third of z alone. However, the last term, in general,

mixes the coordinates. The only way the separation can become complete is

for the last term to be separated as well, that is, expressed as a sum of three

functions, each depending on a single coordinate.

In such a special case we

obtain

+ f

(x)+f

(y)+f

(z)=0



+ f

(x)





+ f

(y)





+ f

(z)



=0.

The ﬁrst term on the LHS depends on x alone, the second on y alone, and

the third on z alone. Since the sum of these three terms is a constant (zero),

independent of all variables, each term must be a constant. Denoting the

constant corresponding to the ith term by −α

,weobtain

+ f

(x)=−α

+ f

(y)=−α

+ f

(z)=−α

which can be reexpressed as

+[f

(x)+α

] X =0,

+[f

(y)+α

] Y =0,

+[f

(z)+α

] Z =0,α

+ α

=0. (22.11)

If f (x, y, z) happens to be a constant C, then the ﬁrst three terms of Equation

(22.10) can be taken to be respectively −α

, −α

,and−α

, leading to

+ α

X =0,

+ α

Y =0,

+ α

Z =0,α

+ α

= C. (22.12)

This is where the limitation of the method of the separation of variables becomes

evident. However, surprisingly, all physical applications, at our level of treatment, involve

functions that are indeed separated.