Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

12.3 The Gradient 359

(x, y, z)

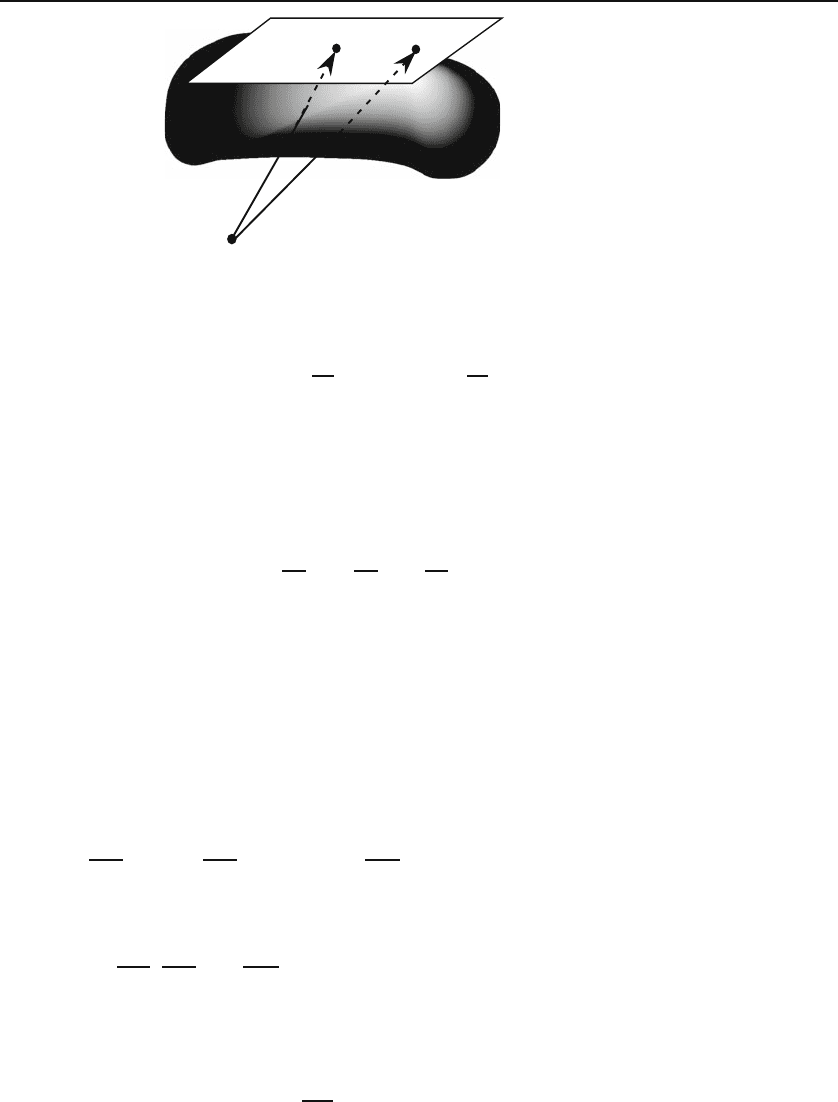
Figure 12.9: The plane tangent to the surface z = g(x, y) at P .

z − z

=(x − x

)



∂g

∂x



+(y − y

)



∂g

∂y





It is convenient to introduce a diﬀerentiation operator which we shall use

later.

the del operator

Deﬁnition 12.3.2. The symbol ∇ can be thought of as a vector operator,

called del or nabla, whose components are ∂/∂x,∂/∂y,and∂/∂z.Thus,we

can write

∇ =

∂

∂x

∂

∂y

∂

∂z

. (12.28)

This vector operator ∇ operates on diﬀerentiable functions and produces vec-

tor ﬁelds.

12.3.1 Gradient and Extremum Problems

The gradient is very nicely used to ﬁnd the maxima and minima of functions

of several variables. A function f(x)ofn variables x =(x

,...,x

)hasa

local extremum (maximum or minimum) at a point a if its diﬀerential vanishes

at that point for arbitrary dx:

df =

∂f

∂x



∂f

∂x



+ ···+

∂f

∂x



≡

∇f(a)

· dx =0

where

∇f ≡



∂f

∂x

∂f

∂x

,...,

∂f

∂x



and dx ≡dx

,dx

,...,dx

.

If the dot product of ∇f (a)anddx is to vanish for arbitrary dx,then∇f(a)

must be zero. Thus for f to have an extremum at a,wemusthave

∇f(a)=0 or

∂f

∂x



=0,i=1, 2,...,n. (12.29)

360 Vectors and Derivatives

This is the generalization to n variables the familiar condition known from

calculus.

In many situations, there are auxiliary conditions or constraints imposed

on the independent variables. For example, let P

, Q,andP

be three points

in space, with P

and P

ﬁxed but Q being allowed to move. Consider the

path P

consisting of straight line segments P

Q and QP

. What choice

of Q gives the shortest path? If we denote the coordinates of Q by (x, y, z)

and those of P

and P

with obvious subscripts, then we have to ﬁnd the

extremum of

f(x, y, z)=



(x − x

)

+(y − y

)

+(z − z

)



(x − x

)

+(y − y

)

+(z − z

)

So we set partial derivatives equal to zero and solve for (x, y, z). The answer,

as expected, turns out to be the path for which Q lies on the line segment

between P

and P

Now suppose we demand that Q lie on a sphere of radius a centered at the

origin. Then the problem becomes extremizing f (x, y, z) with the constraint

condition that

g(x, y, z) ≡ x

+ y

+ z

− a

=0.

To solve this problem, we could solve for one of the variables of the constraint

equation in terms of the other two, substitute in f(x, y, z), and solve the re-

sulting two-variable problem. But there is a much more elegant way involving

gradients, which we discuss now.

Suppose that we want to ﬁnd the extremum of a function f(x)ofn vari-

ables x =(x

,...,x

) subject to the condition that x must lie on the

hypersurface g(x) = 0. We cannot set ∇f equal to zero because dx is no

longer arbitrary.

With constraint, dx is conﬁned to the surface g(x)=0. Now,theonly

n-dimensional vector which has a vanishing dot product with any dx on the

constrained surface is (a multiple of) the normal to the surface. Therefore, if

(∇f)·dx is to be zero for dx lying on the surface, then ∇f must be a multiple

of the normal to the surface g(x) = 0. But this normal is nothing but ∇g.

Therefore, if f is to have an extremum subject to the constraint g(x)=0,

then it must obey the following equation

∇f = −λ∇g or ∇f + λ∇g =0,

where λ is an arbitrary constant called the Lagrange multiplier.This

equation shows that to ﬁnd the extremum of the function f with constraint

g(x) = 0, one can deﬁne the function F of n +1variables

Lagrange

multipliers

F (x

,...,x

; λ) ≡ f(x

,...,x

)+λg(x

,...,x

12.3 The Gradient 361

and extremize it without constraint.Thenwehave

∂F

∂x

∂f

∂x

+ λ

∂g

∂x

=0,i=1, 2,...,n,

∂F

∂λ

= g(x

,...,x

)=0. (12.30)

The last equation is just the constraint condition, but it comes out conve-

niently as one of the extremal equations of F .

Example 12.3.4.

A rectangular box is to be made out of a given amount A of

material to have the largest volume. What dimensions should the box have? Here

f(x, y, z)=xyz,thevolume,andg(x, y, z)=2xy +2xz +2yz − A. Setting the

components of the gradient of

F (x, y, z; λ)=xyz +2λ(xy + xz + yz −A/2)

equal to zero yields four equations

yz +2λ(y + z)=0,

xz +2λ(x + z)=0,

xy +2λ(x + y)=0,

2(xy + xz + yz) − A =0.

Multiplying the ﬁrst equation by x and the second equation by y and subtracting

yields

2λx(y + z) − 2λy(x + z)=0

, or x = y.

Similarly, from the second and third equations we get y = z. So, the box should be

a cube. The last equation then gives

− A =0, or x = y = z =



Substituting this in any of the above equations involving λ yields λ = −



A/6. 

The extremal problems may have several constraint equations such as

,...,x

) ≡ g

(x)=0,j=1, 2,...,m. (12.31)

We can “eliminate” the ﬁrst constraint by replacing f(x

,...,x

)with

(x; λ

) ≡ f(x)+λ

(x),

where F

has only m − 1 constraint equations. Now eliminate the second

constraint by deﬁning

(x; λ

,λ

) ≡ F

(x; λ

)+λ

(x)=f(x)+λ

(x)+λ

(x).

Continuing, we can eliminate all constraints by deﬁning

F (x; λ

,λ

,...,λ

) ≡ f(x)+



j=1

(x), (12.32)

whose unconstrained extremization yields the extremal equations.

362 Vectors and Derivatives

12.4 Problems

12.1. Find directly the solid angle subtended by a disk of radius a at a point

P on its perpendicular axis located a distance b from the center.

12.2. Aclosedcurveρ =3a + a cos ϕ in cylindrical coordinates bounds a

region in the xy-plane. Find the solid angle subtended by this region at a

point P on the z-axis a distance 2a above the xy-plane.

12.3. Derive Equation (12.11).

12.4. Show that when a moving particle is conﬁned to a circle, its velocity is

always perpendicular to its radius. If, furthermore, the speed of the particle

is constant, then its acceleration is radial.

12.5. Derive Equations (12.17) and (12.18).

12.6. The vectors a and b are given by

a = u

+ v

, b = v

− u

(a) Write

and

in terms of Cartesian unit vectors.

(b) Find the four vectors ∂

/∂u, ∂

/∂v, ∂

/∂u,and∂

/∂v in terms of

Cartesian unit vectors.

and

in terms of

and

(d) Express the four vectors ∂

/∂u, ∂

/∂v, ∂

/∂u,and∂

/∂v in terms

and

(e) If u and v are functions of time, ﬁnd d

/dt and d

/dt in terms of

and

12.7. Derive Equation (12.19).

12.8. Derive Equation (12.23).

12.9. Show that (12.22) and the assumption θ = π/2 solve the last two

equations of (12.20) and reduce the ﬁrst one to (12.24).

12.10. (a) Obtain the time derivatives of the cylindrical unit vectors:

=˙ϕ

= − ˙ϕ

=0.

(b) Use the result of (a) to show that if A is a vector written in terms of

cylindrical unit vectors, then



− A

˙ϕ





˙ϕ +



12.11. Asurfaceisgivenby

= 1. Find the unit normal to

the surface and the equation of the tangent plane at (a/2,a,a).

12.4 Problems 363

12.12. The potential of a certain charge distribution is given by

Φ(x, y, z)=z

(a) Find the electric ﬁeld E = −∇Φat(3/

√

2, 1, 1/2) and show that it is

normal to the surface

=1.

(b) Show that the electric ﬁeld is normal at every point of this surface.

by replacing 1 on the RHS of the last equation by any arbitrary constant.

12.13. Show that ∇(fg)=(∇f)g + f(∇g) for any two (diﬀerentiable) func-

tions f and g of (x, y, z).

12.14. Consider the plane ax + by + cz = d and a point P =(x

)

not lying in the plane. Use Lagrange multipliers to show that the parametric

equation of the line passing through P that gives the minimum distance to

the plane is

r = r

+ tn, where r = x, y, z, r

= x

, n = a, b, c.

(12.33)

From this deduce that the distance from P to the plane is

|d −ax

− by

− cz

√

+ b

+ c

Hint: Take the dot product of (12.33) with n and use the fact that n · r = d

when the tip of r is in the plane.

12.15. Consider the sphere (x − a)

+(y − b)

+(z − c)

= d

and a point

P =(x

) not lying on the sphere. Use Lagrange multipliers to show that

the shortest line segment connecting P to the sphere is that which extends

through the center of the sphere.

12.16. For a vector A(r,t) that is a function of position and time, show that

dA =(dr · ∇)A +

∂A

∂t

dt.

12.17. Find the gradient of

u(x, y, z, x



) ≡ u(r − r



)=|r −r



ﬁrst with respect to the components of r and then with respect to the com-

ponents of r



, and write the answer completely in terms of r and r



.Whatis

the answer when m = −1?

Chapter 13

Flux and Divergence

A vector ﬁeld is a function with direction, and because of this directional

property, many new kinds of diﬀerentiation and integration can be performed

on it. For instance, a vector ﬁeld can be made to pierce a surface or an element

thereof, and as it pierces that surface its variation from point to point can be

monitored. This leads to one kind of diﬀerentiation and integration which we

discuss next. The integration leads to the concept of the ﬂux of a vector ﬁeld,

and the associated diﬀerentiation to the notion of divergence.

13.1 Flux of a Vector Field

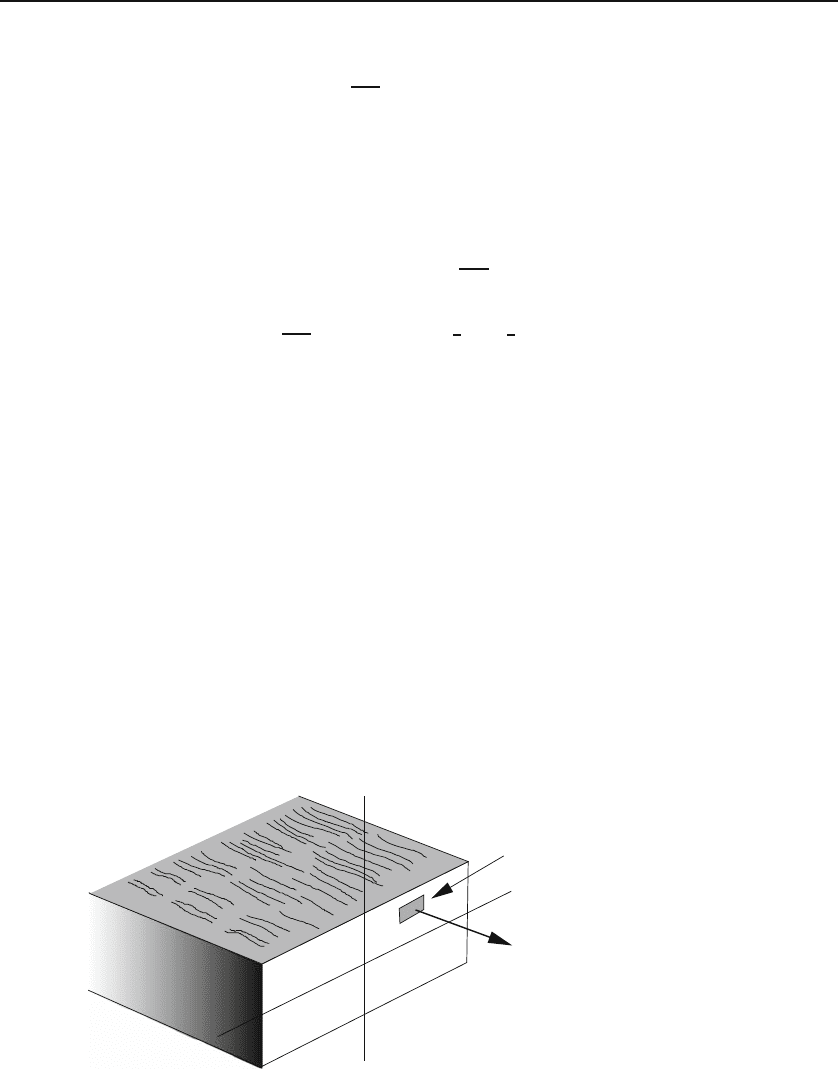
The paradigm of the concept of ﬂux is that of the velocity ﬁeld of a ﬂuid (see

Figure 13.1). A small ring of area Δa is situated in the ﬂow. How much ﬂuid

is passing through the ring per unit time? It is clear that the answer depends

on the density of the ﬂuid,

thespeedoftheﬂuid,thesizeoftheareaΔa,and

also on the relative orientation of the direction of the ﬂow and the unit normal

to the area, denoted by

. A little contemplation reveals that the amount of

ﬂuid of constant unit density passing through Δa is proportional to

ﬂux of ﬂow

velocity through a

small area

Δφ = v ·

Δa ≡ v · Δa, (13.1)

where Δφ is called the ﬂux of v through Δa,andΔa is deﬁned to be

Δa.

If the ring is replaced by a large surface S then we have to divide the surface

into small areas—not necessarily in the shape of a ring—and sum up the con-

tribution of each area to the ﬂux. In the limit of smaller and smaller areas

and larger and larger numbers of such areas, we obtain an integral:

total ﬂux of ﬂow

velocity through a

large area

φ = lim

Δa→0

N→∞



i=1

Δa

≡ lim

Δa→0

N→∞



i=1

·Δa

v ·da, (13.2)

where φ is the total ﬂux through S.

For simplicity we assume that density is constant and we take it to be 1.

We shall come back to a rigorous derivation of the ﬂow of a substance through a small

loop later (see the discussion after Theorem 13.2.2).

366 Flux and Divergence

Figure 13.1: Flux of velocity vector through a small area Δa.

There is an arbitrariness in the direction of the unit vector normal to an

element of area, because for any unit normal, there is another which points in

the opposite direction. The ﬂux for these two unit normals will have opposite

signs. This may appear as if one could arbitrarily choose every one of the

unit normals

in the sum (13.2) to have either one of the two opposite

orientations, leading to an arbitrary result for the integral. This is not the case,

the total ﬂux can

be determined

only up to a sign.

because the direction of the unit normal to an element of area is determined

by the neighboring unit normals and the requirement of continuity. So, once

the choice is made between the two possibilities of the unit normal for one

element of area of the surface S,saytheﬁrstone

, the second one can

diﬀer only slightly from

—in particular, it cannot be of opposite sign. The

third one should point in almost the same direction as the second one, and

so on. This requirement of continuity will uniquely determine the remaining

unit normals. However, the initial choice remains arbitrary, and since the

two orientations of the initial choice diﬀer by a sign, the two total ﬂuxes

corresponding to these two orientations will also diﬀer by a sign. We shall see

shortly, however, that for closed surfaces, such an arbitrariness in sign can be

overcome by convention.

The discussion above works for orientable surfaces. This means that on

orientable surface

any closed loop entirely on the surface, the direction of a normal vector will

not change when one displaces it on the loop continuously one complete orbit.

It is clear that the lateral surface of a cylinder is orientable.

A cylinder is obtained by glueing the two edges of a rectangle. Now take

the same rectangle and twist one of the (smaller) edges before glueing it to the

opposite edge. The result—which the reader may want to construct—is a very

famous mathematical surface called the M¨obius band.AM¨obius band is not

M¨obius band

orientable, because if one starts at the midpoint of the glued edges and moves

perpendicular to it along the large circle (length of the original rectangle),

then a unit normal displaced continuously and completely along the circle

will be ﬂipped.

In this book we shall never encounter nonorientable surfaces.

The reader is urged to perform this surprising experiment using a (portion of a) tooth-

pick as a unit normal.

13.1 Flux of a Vector Field 367

Example 13.1.1. Consider the ﬂow of a river and assume that the velocity of the

water is given by

v = v



1 −



where x is the distance from the midpoint of the river and w is the width of the

river. Let us ﬁnd the ﬂux of the velocity, assuming that the cross section of the river

is a rectangle with depth equal to h, as shown in Figure 13.2.

The normal to the area da is perpendicular to the xy-planeandisinthesame

direction as the velocity. Thus, we have v · da = vda= vdxdy,and

φ =

vdxdy=

h/2

−h/2

w/2

−w/2



1 −



= hv

w/2

−w/2



1 −



dx = hv

(w −

w)=

where S is the cross section of the river and A is its area.



The concept of ﬂux, although indicative of a ﬂow, is not limited to the

velocity vector ﬁeld. We can deﬁne the ﬂux of any vector ﬁeld A in exactly

ﬂux can be deﬁned

not only for

velocity, but for

any vector ﬁeld.

the same way:

φ =

A ·da. (13.3)

Whether such a deﬁnition is useful or not should be determined by experi-

ment. It turns out that the ﬂux of every physically relevant vector ﬁeld is

not only useful, but essential for the theoretical—as well as experimental—

investigation of that ﬁeld. For example, the ﬂux of a gravitational ﬁeld

through a closed surface is related to the amount of mass in the volume

enclosed in the surface. Similarly, the rate of change of the ﬂux of a magnetic

ﬁeld through a surface gives the electric ﬁeld produced at the boundary of the

surface.

da = dx dy

Figure 13.2: The river with its cross section.

368 Flux and Divergence

Figure 13.3: The ﬂux of the electric ﬁeld through a circle. The normal unit vector

could be chosen to be either up or down. We choose (quite arbitrarily) the up direction

to make the ﬂux positive for positive q.

Example 13.1.2. Consider the ﬂux of the electric ﬁeld of a point charge located

at a distance d from the center of a circle of radius a as shown in Figure 13.3. The

element of ﬂux is given by

E · da = |E|cos θda = |E|cos θρdρdϕ =

ρdρdϕ =

kqd

+ ρ

)

3/2

ρdρdϕ,

where

is chosen to point up. The polar coordinates (ρ, ϕ) are used to specify a

point in the plane of the circle at which point the element of area is ρdρdϕ. To ﬁnd

the total ﬂux, we integrate the last expression above:

φ =

kqd

+ ρ

)

3/2

ρdρdϕ = kqd

2π

dϕ

ρdρ

+ ρ

)

3/2

=2πkqd

−(d

+ ρ

)

−1/2



=2πkq



1 −

√

+ a



Note that since d represents a distance, as opposed to a coordinate, it is always

positive and d =

√

= |d|.



It is often necessary to calculate the ﬂux of a vector ﬁeld through a closed

surface bounding a volume. Intuitively, such a ﬂux gives a measure of the

for a closed

surface, one can

uniquely

determine the

direction of

normal at each

point of the

surface.

strength of the source of the vector ﬁeld in the volume. For instance, the ﬂux

of the velocity ﬁeld of water through a closed surface bounding a fountain

measures the rate of the water output of the fountain. If the surface does

not enclose the fountain, the net ﬂux will be zero because the ﬂux through

one “side” of the closed surface will be positive and that of the other “side”

will be negative with the total ﬂux vanishing. In the case of an electrostatic

ﬁeld, the ﬂux through a closed surface measures the amount of charge in the

volume bounded by that surface. The sign of the ﬂux requires an orientation

of the bounding surface which is equivalent to the assignment of a positive

direction to the unit normal to the surface at each of its points. We agree to

out is positive!

adhere to the convention of Box 12.1.3.

Only orientable surfaces can have a well deﬁned orientation. Since we are excluding

nonorientable surfaces from this book, all our surfaces respect Box 12.1.3.

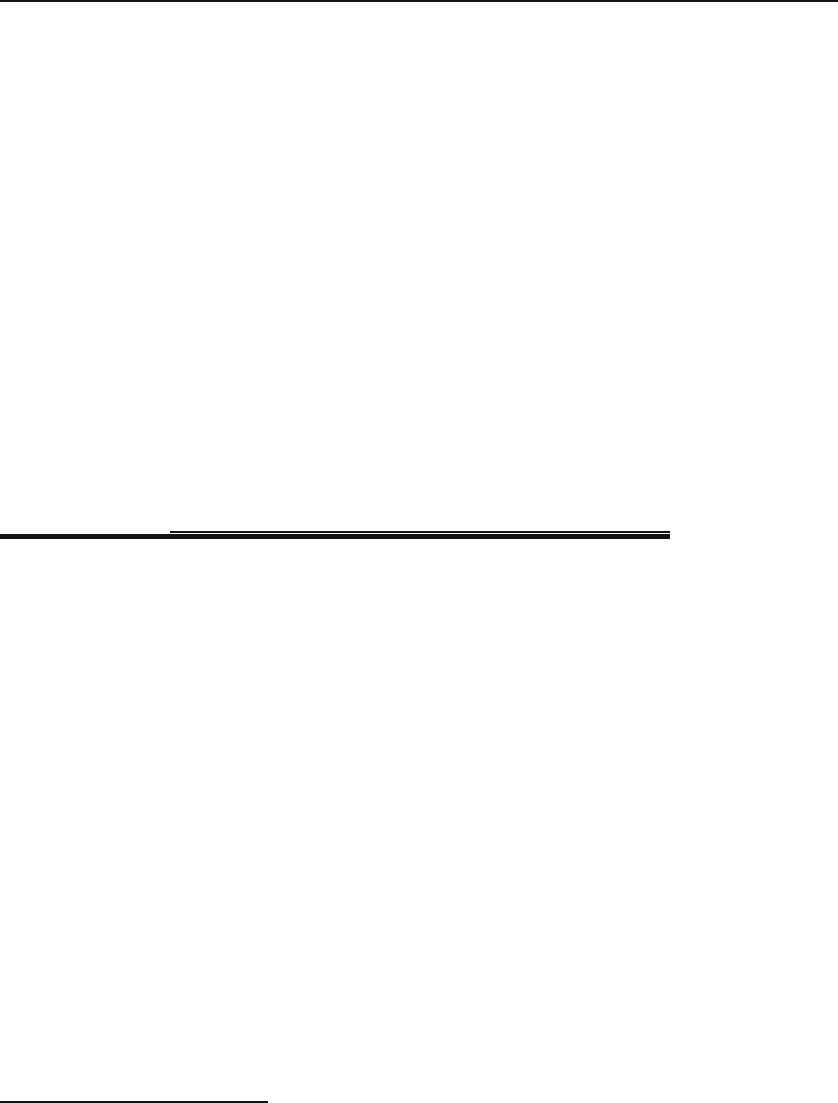
13.1 Flux of a Vector Field 369

Example 13.1.3. Let us consider the ﬂux through a sphere of radius a centered

at the origin of a vector ﬁeld A given by A = kQr

with k a proportionality

constant and Q the strength of the source. Assuming that the outward normal is

considered positive (see Box 12.1.3) the total ﬂux through the sphere is calculated

A · da =

kQa

· (

sin θdθdϕ)

= kQ

2π

dϕ

sin θdθ =2πkQa

m+2

sin θdθ=4πkQa

m+2

It is important to keep in mind that when calculating the ﬂux of a vector ﬁeld, one remember to

evaluate the

vector ﬁeld at the

surface when

calculating its

ﬂux!

has to evaluate the ﬁeld at the surface.Thatiswhya appears in the integral rather

than r. Notice how the ﬂux depends on the radius of the sphere. If m +2> 0, then

the farther away one moves from the origin, the more total ﬂux passes through the

sphere. On the other hand, if m +2< 0, although the size of the sphere increases,

and therefore, more area is available for the ﬁeld to cross, the ﬁeld decreases too

rapidly to give enough ﬂux to the large sphere, so the ﬂux decreases. The important

case of m = −2 eliminates the dependence on a: The total ﬂux through spheres of

diﬀerent sizes is constant. This last statement is a special case of the content of the

celebrated Gauss’s law.



Historical Notes

Space vectors were conceived as three-dimensional generalizations of complex num-

bers. The primary candidates for such a generalization however turned out to be

quaternions—discovered by Hamilton—which had four components. One could nat-

urally divide a quaternion into its “scalar” component and its vector component,

the latter itself consisting of three components. The product of two quaternions,

being itself a quaternion, can also be divided into scalar and vector parts. It turns

out that the scalar part of the product contains the dot product of the vector parts,

and the vector part of the product contains the cross product of the vector parts.

However, the full product contains some extra terms.

Physicists, on the other hand, were seeking a concept that was more closely

associated with Cartesian coordinates than quaternions were. The ﬁrst step in this

direction was taken by James Clerk Maxwell. Maxwell singled out the scalar and the

vector parts of Hamilton’s quaternion and put the emphasis on these separate parts.

In his celebrated A Treatise on Electricity and Magnetism (1873) he does speak of

quaternions but treats the scalar and the vector parts separately.

Hamilton also developed a calculus of quaternions. In fact, the gradient operator

introduced in Deﬁnition 12.3.2 and its name “nabla” were both Hamilton’s inven-

tion.

Hamilton showed that if ∇ acts on the vector part v of a quaternion, the

result will be a quaternion. Maxwell recognized the scalar part of this quaternion

to be the divergence (to be discussed in the next section) of the vector v,andthe

vector part to be the curl (to be discussed in the Section 14.2) of v.

Maxwell often used quaternions as the basic mathematical entity or he at least

made frequent reference to quaternions, perhaps to help his readers. Nevertheless,

his work made it clear that vectors were the real tool for physical thinking and not

just an abbreviated scheme of writing, as some mathematicians maintained. Thus

He used the word “nabla” because ∇ looks like an ancient Hebrew instrument of that

name.