Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

11.3 Problems 337

11.5. Show that

Γ(x)=2

∞

−t

2x−1

and

Γ(x)=

(



)

x−1

dt.

11.6. Find the following integrals in terms of the gamma function:

(a)



∞

2x+1

−at

dt. (b)



∞

−at

dt.

11.7. Using only its integral representation, show that beta function is sym-

metric under interchange of its arguments.

11.8. Using the deﬁnition of the gamma function, show the justiﬁcation for

the frequently used equality 0! = 1.

11.9. Show that



1+k

sin

tdt=



1+k

E(k



) −E



− ϕ, k



+

where k



= k/

√

1+k

. Hint: Change t to s = π/2 − t and break up the

interval of integration of the resulting integral into two.

11.10. Show that the circumference of an ellipse of respective semi-major and

semi-minor axes a and b is 4aE(k)wherek =

√

− b

/a.Verifythatyou

get the expected result when a = b.

11.11. (a) Expand the square roots in the deﬁnition of the elliptic integrals

of the ﬁrst and second kinds in powers of k

sin

t, and keep the ﬁrst three

terms.

(b) Now integrate those terms to ﬁnd an approximation to elliptic integrals

for small k.

integrals.

11.12. Use the result of Problem 11.11 to obtain Equation (11.21).

11.13. Use the integral

π/2

sin

tdt =

(2n −1)!!

(2n)!!

to show that

E(k)=

1 −

∞



n=1



(2n −1)!!

(2n)!!



2n −1

K(k)=

∞



n=1



(2n −1)!!

(2n)!!



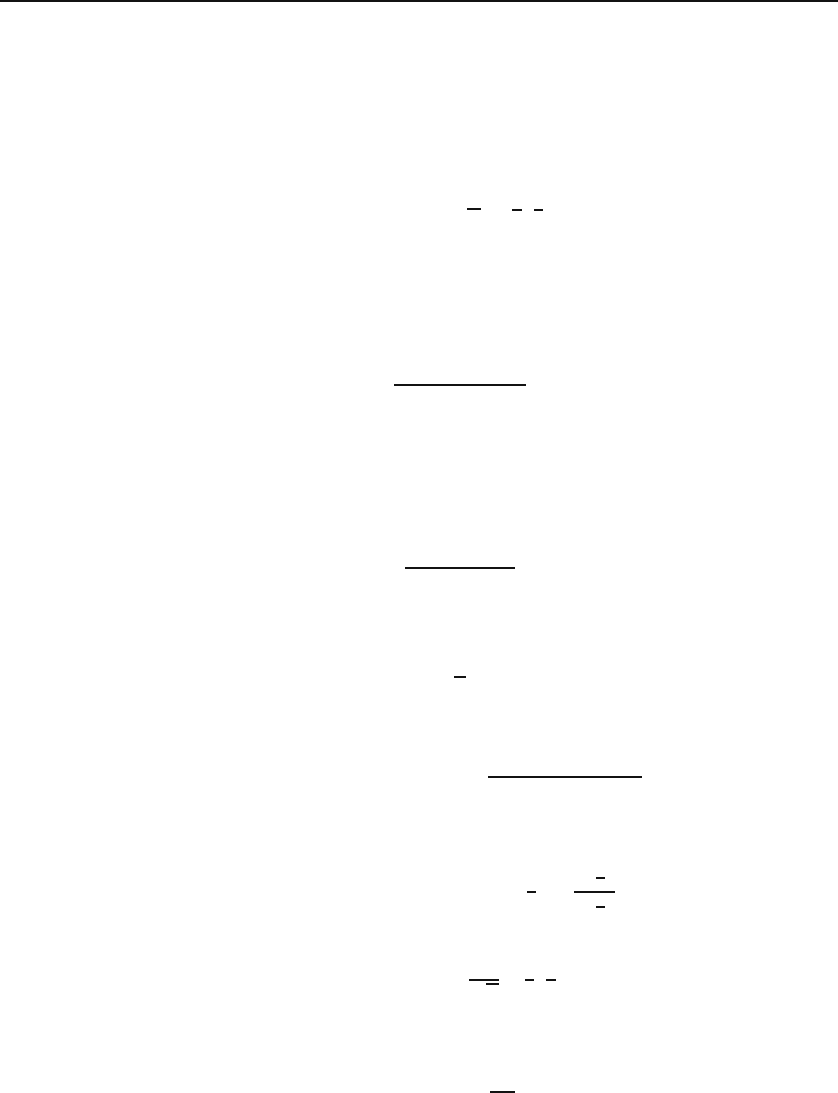
338 Integrals and Series as Functions

11.14. Show that E(0) = K(0) = π/2, and that E(1) = 1, K(1) = ∞.

11.15. Use the ratio test on the hypergeometric series to determine its radius

of convergence.

11.16. Verify that the complete elliptic integral of the ﬁrst kind is related to

the hypergeometric function as follows:

K(k)=

;1;k

11.17. Show that ln(1 + x)=xF (1, 1; 2; −x).

11.18. Use the result of Problem 11.4 to express Equation (10.15) of Chapter

10 in terms of the gamma function; then show that

(1 + x)

∞



n=0

Γ(n −α)

Γ(−α)Γ(n +1)

(−x)

= F (−α, β; β; −x)

for arbitrary β.

11.19. By using integral representations:

(a) Show that

B(a, b)=

Γ(a)Γ(b + r)

Γ(a + b + r)

F (a, r; a + b + r;1),

where B is the beta function and r is any real number. Choose r appropriately

and show that

B(a, b)=

F (a, 1 − b; a +1;1).

(b) Also prove that

F (α, β; γ;1)=

Γ(γ)Γ(γ −α − β)

Γ(γ − α)Γ(γ − β)

11.20. Expand the integrand of erf(x) in its Maclaurin series and use

2n +1=2(n +

Γ(

)

Γ(

)

to show that

erf(x)=

√

Φ(

;

; −x

11.21. Using the same procedure as in Example 11.2.1, show that

−1/2



πx



1/2

cos x.

11.3 Problems 339

11.22. Show that

k!Γ(m + k)

−

(k − 1)!Γ(m + k +1)

k!Γ(m + k +1)

and use it to derive Equation (11.35).

11.23. Derive Equation (11.36).

11.24. Find J

3/2

(x)andJ

−3/2

(x). Hint: Use Equation (11.37).

Part IV

Analysis of Vectors

Chapter 12

Vectors and Derivatives

One of the basic tools of physics is the calculus of vectors. A great variety

of physical quantities are vectors which are functions of several variables such

as space coordinates and time, and, as such, are good candidates for mathe-

matical analysis. We have already encountered examples of such analyses in

our treatment of the integration of vectors as in calculating electric, magnetic,

and gravitational ﬁelds. However, vector analysis goes beyond simple vector

integration. Vectors have a far richer structure than ordinary numbers, and,

therefore, allow a much broader range of concepts.

Fundamental to the study of vector analysis is the notion of ﬁeld,with

which we have some familiarity based on our study of Chapters 1 and 4.

Fields play a key role in many areas of physics: In the motion of ﬂuids, in the

conduction of heat, in electromagnetic theory, in gravitation, and so forth. All

these situations involve a physical quantity that varies from point to point as

well as from time to time,

i.e., it is a function of space coordinates and time.

This physical quantity can be either a scalar, in which case we speak of a

scalar ﬁeld, or a vector, in which case we speak of a vector ﬁeld.Thereare

scalar and vector

ﬁelds

also tensor ﬁelds, which we shall discuss brieﬂy in Chapter 17, and spinor

ﬁelds, which are beyond the scope of this book.

The temperature of the atmosphere is a scalar ﬁeld because it is a function

of space coordinates—equator versus the poles—and time (summer versus

winter), and because temperature has no direction associated with it. On the

other hand, wind velocity is a vector ﬁeld because (a) it is a vector and (b) its

magnitude and direction depend on space coordinates and time. In general,

when we talk of a vector ﬁeld, we are dealing with three functions of space

and time, corresponding to the three components of the vector.

In many instances ﬁelds are independent of time in which case we call them static

ﬁelds.

344 Vectors and Derivatives

12.1 Solid Angle

Before discussing the calculus of vectors, we want to introduce the concept of

a solid angle which is an important and recurrent concept in mathematical

physics, especially in the discussion of vector calculus.

12.1.1 Ordinary Angle Revisited

We start with the concept of angle from a new perspective which easily gener-

alizes to solid angle. Consider a curve and a point P in a plane. The point P

concept of angle

reexamined

is taken to lie oﬀ the curve [Figure 12.1(a)]. An arbitrary segment of the curve

deﬁnes an angle which is obtained by joining the two ends of the segment to

P . In particular, an element of length along the curve deﬁnes an inﬁnitesimal

angle. We want to relate the length of this element to the size of its angle

measured in radians.

Connect P to the midpoint of the inﬁnitesimal line element of length Δl,

and call the resulting vector R with the corresponding unit vector

as shown

in Figure 12.1(a).

Let the angle between

and the unit normal

to the

length element

be α. As shown in the magniﬁed diagram of Figure 12.1(b),

α is also the angle between the line element



and the line segment obtained

by dropping a perpendicular

QH onto the ray PQ



. It is clear from the

diagram that

QH = QQ



cos α ⇒ QH =Δl cos α =Δl

Now recall that the measure of an angle in radians is given by the ratio of

the length of the arc of a circle subtended by the angle to the radius of the

circle, and this measure is independent of the size of the circle chosen. To

ﬁnd the measure of Δθ in radians, let us choose a circle of radius R = |R|,

(a)

(b)

Δθ

to P

dl cos α

Figure 12.1: Deﬁning angles as ratios of lengths.

In actual calculations, it is convenient to denote the position vector of P by r,say,and

that of the midpoint by r



.ThenR = r



− r.

There are two possible directions for this unit normal: one as shown in Figure 12.1,

and the other in the opposite direction. As long as we deal with open curves (no loops)

this arbitrariness persists.

12.1 Solid Angle 345

the distance from P to the midpoint of the line element. The arc of this circle

subtended by Δθ is CC



, and the ﬁgure shows that the length of this arc is

very nearly equal to

QH. One can think of CC



as the projection of the line

element onto the circle. Thus,

Δθ ≈

Δl

If we denote the location of P by r and that of Δl by r



,then

R = r



− r,



− r



− r|

and we obtain

Δθ =

Δl(r



)

· (r



− r)



− r|

, (12.1)

where we have emphasized the dependence of Δl on r



For a ﬁnite segment of the curve, we integrate to obtain the angle. This

yields

angle as integral

θ =

dl(r



)

· (r



− r)



− r|

, (12.2)

where a and b are the beginning and the end of the ﬁnite segment. There is a

way of calculating this ﬁnite angle which, although extremely simple-minded,

is useful when we generalize to solid angle. Since the size of the circle used to

measure the angle is irrelevant, let us choose a single ﬁducial circle of radius a

centered at P (see Figure 12.2). Then, as we project elements of length from

the curve, we obtain inﬁnitesimal arcs of this circle with the property that

dθ =

where dl

is the element of arc of the ﬁducial circle. From this equation, we

obtain

θ =



, (12.3)

where a



and b



are projections of a and b on the circle, and s is the length of

the arc from a



to b



. This last relation is, of course, our starting point where

we deﬁned the measure of an angle in radians!

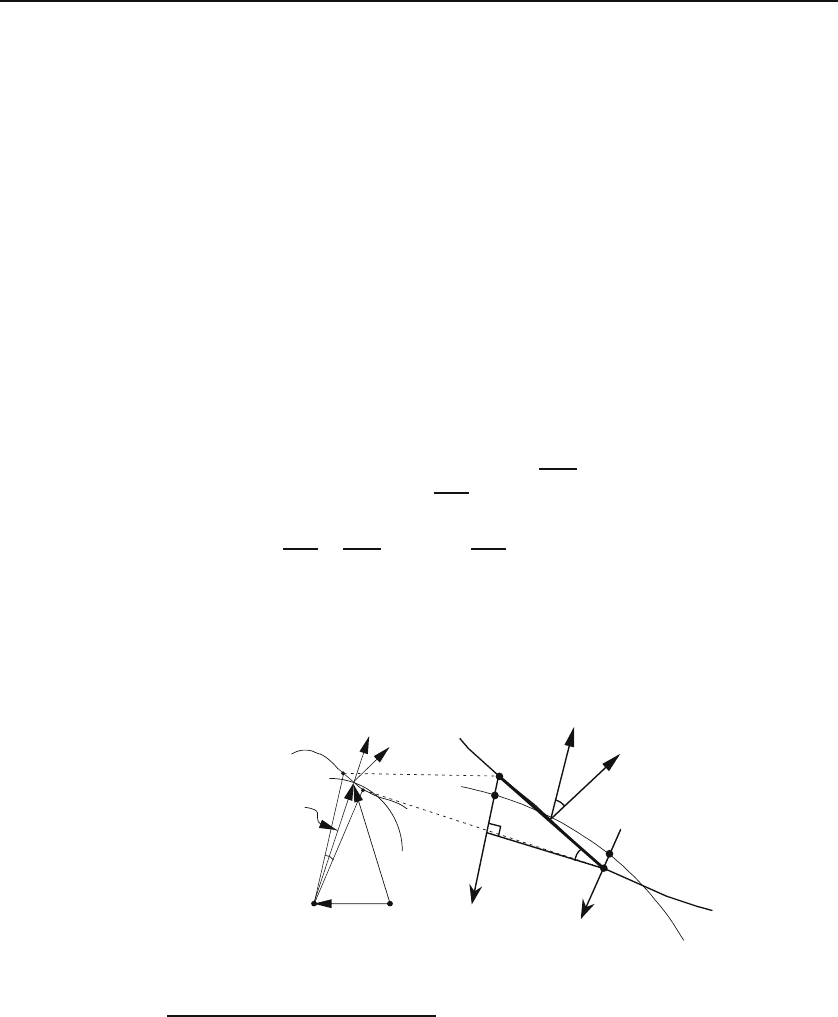
Of special interest is the case where the curve loops back on itself. For

such a case, the direction of

is predetermined by

Box 12.1.1. (Convention). We agree that for angle calculations, the

unit normal shall always point out of a closed loop.

346 Vectors and Derivatives

′

(a)

(b)

Figure 12.2: Total angle subtended by a closed curve about a point (a) inside and (b)

outside.

If P happens to be inside the loop [Figure 12.2(a)], the total angle, corre-

sponding to a complete traversal of the loop, is

θ =

2πa

=2π.

When P is outside,wegetθ = 0. This can be seen in Figure 12.2(b) where the

projection of the closed curve covers only a portion of the ﬁducial circle and it

does so twice, once with a positive sign—when

and

are separated by an

acute angle—and once with a negative sign—when

and

are separated

by an obtuse angle. Let us denote by θ

the total angle subtended by the

closed curve C about a point P and by U the region enclosed by C. Then,

we have

total angle at a

point subtended

by a closed curve

2π if P is in U,

0ifP is not in U.

(12.4)

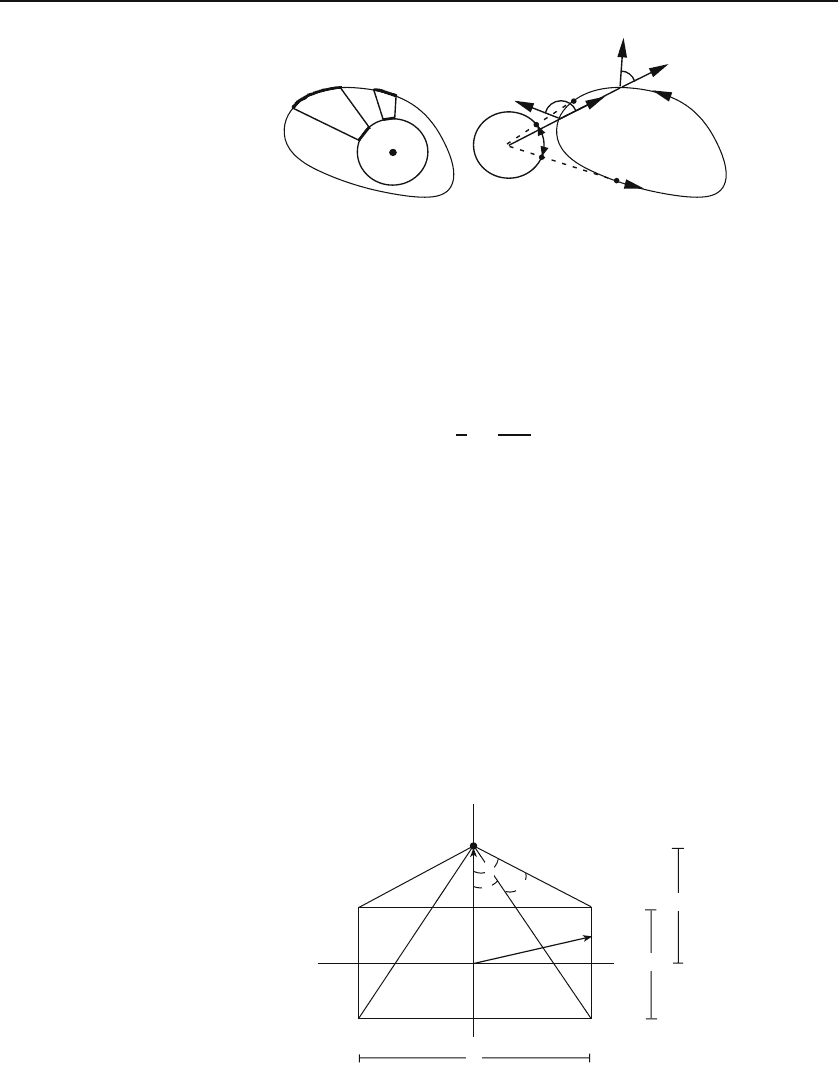
Example 12.1.1.

Point P is located outside a rectangle of sides 2a and 2b as

shown in Figure 12.3. We want to verify Equation (12.4). The integration is nat-

urally divided into four regions: right, top, left, and bottom. We shall do the

′

Figure 12.3: Total angle subtended by a rectangle about a point outside.

12.1 Solid Angle 347

right-hand-side integration in detail, leaving the rest for the reader to verify. For

the right side we have r = y

, r



= a

+ y



,and

dl =+dy



, R = r



− r = a, y



− y

,

Therefore,

dθ



R ·

ady



+(y



− y

)

and the total integrated angle for the right side is

= a

−b



+(y



− y

)

=∠ CBP

  

tan

−1



+ b



−

=∠ DAP

  

tan

−1



− b



− α −



− β



= β − α.

Similarly, one can easily show that θ

= −2β, θ

= β − α,andθ

=2α,wheret

stands for “top,” l for “left,” and b for “bottom.” The total subtended angle is,

therefore zero, as expected. Note that only for the top side is the angle between

and

obtuse, and this fact results in the negative value for θ



The purpose of the whole discussion of the ordinary angle in such a high-

brow fashion and detail has been to lay the ground work for the introduction

of the solid angle. As we shall see shortly, a good understanding of the new

properties of the ordinary angle discussed above makes the transition to the

solid angle almost trivial.

12.1.2 Solid Angle

We are now ready to generalize the notion of the angle to one dimension

higher. Instead of a curve we have a surface, instead of a line element we have

an area element, and instead of dividing by R we need to divide by R

.This

last requirement is necessary to render the “angle” dimensionless. Referring

to Figure 12.4,

solid angle deﬁned

Figure 12.4: Solid angle as the ratio of area to distance squared.

348 Vectors and Derivatives

Box 12.1.2. We deﬁne the solid angle subtended by the element of area

Δa as

ΔΩ ≈

Δa

· Δa



− r) · Δa



− r|

where

is the unit normal to the surface and Δa ≡

Δa(r



The numerator is simply the projection of Δa onto a sphere of radius R

as Figure 12.5 shows. This projection is obtained by the intersection of the

ﬁducial sphere and the rays drawn from P to the boundary of Δa.Asinthe

case of the angle, the choice of ﬁducial sphere is arbitrary. The integral form

of the above equation is

Ω=

· da

R · da



− r) · da(r



)



− r|

, (12.5)

where S is the surface subtended by the solid angle Ω.

Box 12.1.3. (Convention). For any closed surface S,wetake

to be

pointing outward.

If we use a single ﬁducial sphere of radius b for all points of S,weobtain

Ω=

da =

, (12.6)

where S

is the projection of S onto the ﬁducial sphere and A its area. This

equation is the analog of Equation (12.3) and can be used to deﬁne the measure

Figure 12.5: The relation between the

·Δa and its projection on a ﬁducial sphere.