Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

Chapter 11

Integrals and Series as

Functions

The notion of a function as a mathematical entity has a long history as rich as

the history of mathematics itself. With the invention of the coordinate plane in

the seventeenth century, functions started to acquire graphical representations

which, in turn, facilitated the connection between algebra and geometry. It

was really calculus that triggered an explosion in function theory, and indeed,

in all mathematics. With calculus came not only the concept of diﬀerentiation

and integration, but also—in the hands of Newton and his contemporaries,

as they were studying no smaller an object than the universe itself—that

of diﬀerential equations. All these concepts, in particular integration and

diﬀerential equation, had a dramatic inﬂuence on the notion of functions. The

aim of this chapter is to give the reader a ﬂavor of the variety of functions

made possible by integration and diﬀerential equations.

11.1 Integrals as Functions

Integrals are one of the most convenient media in which new functions can be

deﬁned. As we saw in Chapter 3, if the integrand or the limits of integration

include parameters, those parameters can be treated as variables and the

integral itself as a function of those parameters. In this section, we list some

of the most important functions that are normally deﬁned in terms of integrals.

We shall not solve any diﬀerential equations in this chapter, but simply quote solutions

to some of them in the form of power series. We shall come back to diﬀerential equations

later in the book.

318 Integrals and Series as Functions

11.1.1 Gamma Function

Consider the integral

Γ(x) ≡

∞

x−1

−t

dt, (11.1)

where x is a real number.

Integrate Equation (11.1) by parts with u = t

x−1

equation (11.1)

deﬁnes the

gamma function

evaluated at x.

and dv = e

−t

dt to obtain

Γ(x)=

≡uv

  

x−1

[−e

−t

]



∞

  

+(x −1)

∞

≡−vdu

  

x−2

−t



 

=Γ(x−1)

Γ(x)=(x −1)Γ(x −1). (11.2)

In particular, if x is a positive integer n, then repeated use of Equation (11.2)

gives

Γ(n)=(n − 1)Γ(n − 1) = (n − 1)(n − 2)Γ(n − 2)

=(n − 1)(n − 2) ···1 · Γ(1) = (n − 1)!,

where we used the fact that Γ(1) = 1 as the reader may easily verify using

Equation (11.1). This equation is written as

for integers, the

gamma function

becomes a

factorial.

Γ(n +1)=n! for positive integer n. (11.3)

Let us rewrite (11.2) as Γ(x − 1) = Γ(x)/(x −1). Then,

lim

x→1

Γ(x − 1) = lim

x→1

Γ(x)

x − 1

→∞

because Γ(1) = 1. Thus, Γ(0) = ∞. Similarly,

lim

x→0

Γ(x − 1) = lim

x→0

Γ(x)

x − 1

→

Γ(0)

−1

→∞,

i.e., Γ(−1) = ∞. It is clear that Γ(n)=∞ for any negative integer n or zero.

It turns out that these are the only points at which Γ(x) is not deﬁned.

Deﬁnition 11.1.1. The function deﬁned by Equation (11.1) is called the

gamma function, which, because it satisﬁes Equation (11.3), is the gener-

alization of the factorials to noninteger values. We sometimes write

Γ(x +1)=x! for any real x (11.4)

and call Γ the factorial function. The gamma function is deﬁned for all

values of its argument except zero and negative integers, for which the gamma

function becomes inﬁnite.

The most complete analytic discussion of Γ(z) allows z to be complex and uses the

full machinery of complex calculus. Here, we shall avoid such completeness and refer the

reader to Hassani, S. Mathematical Physics: A Modern Introduction to Its Foundations,

Springer-Verlag, 1999, where a full discussion of Γ(z) can be found in Section 11.4.

11.1 Integrals as Functions 319

It follows from Equation (11.2) that by repeatedly subtracting 1 from the the values of Γ(x)

for 0 <x≤ 1

determine Γ(x)

for all x.

argument of the gamma function, we can reduce the evaluation of Γ(x)tothe

case where x lies between 0 and 1. Such an evaluation can be done numerically

and the results tabulated.

Example 11.1.1.

In this example, we evaluate Γ(

). Equation (11.1) gives

Γ(

∞

−1/2

−t

dt.

Change the variable of integration to u =

√

t with du =(1/2

√

t) dt.Then

Γ(

)=2

∞

−u

du =2

√

π,

whereweusedtheresultofExample3.3.1.

With Γ(

) at our disposal, we can evaluate the gamma function at any half-

integer value by the remarks above. For example,

Γ(

)=(

)(

)Γ(

)=(

)(

)Γ(

√

Similarly, with Γ(

)=−

Γ(−

), we obtain

Γ(−

)=−2Γ(

)=−2

√

π.



It is instructive to generalize the result of the example above and ﬁnd a

general formula for the gamma function of any half-integer. Such a formula

is related to the notion of the double factorial:

double factorial

Deﬁnition 11.1.2. The double factorial (2n)!! [or (2n −1)!!] is deﬁned as

the product of all even (or odd) integers up to 2n (or 2n −1).

Problem 11.1 gives the detail of the derivation of the following formulas:

(2n)!! = 2

n!=2

Γ(n +1), (2n −1)!! = Γ(n +

−1/2

. (11.5)

An extremely useful approximation to the gamma function is the so-called

Stirling approximation which is valid for large arguments of the gamma

Stirling

approximation

function and which we present without derivation

x! ≡ Γ(x +1)≈

√

2πe

−x

x+1/2

. (11.6)

The Stirling formula works best when x is large. However, even for x = 10,

it gives

√

2πe

−10

10.5

= 3598696, which is surprisingly close to the exact

value of 10! = 3628800. For x = 20, the Stirling formula yields 2.42 × 10

to three signiﬁcant ﬁgures as opposed to the calculator result, which to the

same number of signiﬁcant ﬁgures is 2.43 ×10

. For larger and larger values

of x, the two results get closer and closer.

For a derivation, see Hassani, S. Mathematical Physics: A Modern Introduction to Its

Foundations, Springer-Verlag, 1999, Chapter 11.

320 Integrals and Series as Functions

11.1.2 The Beta Function

A function that sometimes shows up in applications is the beta function.

Consider

Γ(x)Γ(y)=

∞

x−1

−t

∞

y−1

−s

ds =

∞

x−1

y−1

−(t+s)

dt ds.

Introduce the new variable u = t+s and use it to rewrite the s integral. Since

the lower limits of both s and t are 0, the lower limit of the u integral will

also be 0. Similarly, the upper limit of u will be inﬁnity. However, since s

and t are positive and their sum is u, the upper limit of t cannot exceed u.

Therefore,

Γ(x)Γ(y)=

∞

dt t

x−1

(u − t)

y−1

−u

Now introduce another variable w by t = uw. Since in the t integration, u is

held constant, we have dt = udw, and the limits of integration for w are 0

and 1. This will allow us to write

Γ(x)Γ(y)=

∞

du e

−u

x+y−1

  

≡Γ(x+y)

dw w

x−1

(1 −w)

y−1

The last integral deﬁnes the beta function. So,

beta function

deﬁned

B(x, y) ≡

Γ(x)Γ(y)

Γ(x + y)

dt t

x−1

(1 −t)

y−1

, (11.7)

where we changed the (dummy) variable of integration from w to t.

We can ﬁnd another representation of the beta function by substituting

t =sin

θ.Then

dt =2sinθ cos θ, 1 −t =1− sin

θ =cos

θ,

and the limits of integration become 0 and π/2. So,

B(x, y)=2

π/2

(sin θ)

2x−1

(cos θ)

2y−1

dθ. (11.8)

Historical Notes

Integration and diﬀerentiation and the whole machinery of calculus opened up en-

tirely new ways of deﬁning functions. Of these, one of the most important is the

gamma function, which arose from work on two problems, interpolation theory and

antidiﬀerentiation. The problem of interpolation had been considered by James Stir-

ling (1692–1770), Daniel Bernoulli (1700–1782), and Christian Goldbach.Itwasposed

to Euler and he announced his solution in a letter of October 13, 1729, to Goldbach.

A second letter, of January 8, 1730, brought in the integration problem.

11.1 Integrals as Functions 321

The interpolation problem had to do with giving meaning to n! for nonintegral

values of n, and the integration problem was the evaluation of an integral already

considered by Wallis,namely

(1 − t)

dt.

Euler showed that this integral led to our integral (11.1).

Leonhard Euler was Switzerland’s foremost scientist and one of the three

greatest mathematicians of modern times (Gauss and Riemann being the other two).

He was perhaps the most proliﬁc author of all time in any ﬁeld. From 1727 to 1783

his writings poured out in a seemingly endless ﬂood, constantly adding knowledge

to every known branch of pure and applied mathematics, and also to many that

were not known until he created them. He averaged about 800 printed pages a

year throughout his long life, and yet he almost always had something worthwhile

to say. The publication of his complete works was started in 1911, and the end

is not in sight. This edition was planned to include 887 titles in 72 volumes, but

since that time extensive new deposits of previously unknown manuscripts have been

unearthed, and it is now estimated that more than 100 large volumes will be required

for completion of the project. Euler evidently wrote mathematics with the ease and

ﬂuency of a skilled speaker discoursing on subjects with which he is intimately

familiar. His writings are models of relaxed clarity. He never condensed, and he

reveled in the rich abundance of his ideas and the vast scope of his interests. The

French physicist Arago, in speaking of Euler’s incomparable mathematical facility,

remarked that “He calculated without apparent eﬀort, as men breathe, or as eagles

sustain themselves in the wind.” He suﬀered total blindness during the last 17 years

of his life, but with the aid of his powerful memory and fertile imagination, and

with assistants to write his books and scientiﬁc papers from dictation, he actually

increased his already prodigious output of work.

Leonhard Euler

1707–1783

Euler was a native of Basel and a student of Johann Bernoulli at the University,

but he soon outstripped his teacher. He was also a man of broad culture, well

versed in the classical languages and literatures (he knew the Aeneid by heart),

many modern languages, physiology, medicine, botany, geography, and the entire

body of physical science as it was known in his time. His personal life was as placid

and uneventful as is possible for a man with 13 children.

Though he was not himself a teacher, Euler has had a deeper inﬂuence on the

teaching of mathematics than any other person. This came about chieﬂy through

his three great treatises: Introductio in Analysin Inﬁnitorum (1748); Institutiones

Calculi Diﬀerentialis (1755); and lnstitutiones Calculi Integralis (1768–1794). There

is considerable truth in the old saying that all elementary and advanced calculus

textbooks since 1748 are essentially copies of Euler or copies of copies of Euler.

These works summed up and codiﬁed the discoveries of his predecessors, and are

full of Euler’s own ideas. He extended and perfected plane and solid analytic geom-

etry, introduced the analytic approach to trigonometry, and was responsible for the

modern treatment of the functions ln x and e

. He created a consistent theory of

logarithms of negative and imaginary numbers, and discovered that ln x has an inﬁ-

nite number of values. It was through his work that the symbols e, π,andi =

√

−1

became common currency for all mathematicians, and it was he who linked them

together in the astonishing relation e

iπ

= −1. Among his other contributions to

standard mathematical notation were sin x,cosx, the use of f(x) for an unspeciﬁed

function, and the use of



for summation.

322 Integrals and Series as Functions

His work in all departments of analysis strongly inﬂuenced the further develop-

ment of this subject through the next two centuries. He contributed many important

ideas to diﬀerential equations, including substantial parts of the theory of second-

order linear equations and the method of solution by power series. He gave the ﬁrst

systematic discussion of the calculus of variations, which he founded on his basic

diﬀerential equation for a minimizing curve. He discovered the integral deﬁning the

gamma function and developed many of its applications and special properties. He

also worked with Fourier series, encountered the Bessel functions in his study of the

vibrations of a stretched circular membrane, and applied Laplace transforms to solve

diﬀerential equations—all before Fourier, Bessel, and Laplace were born.

E. T. Bell, the well-known historian of mathematics, observed that “One of the

most remarkable features of Euler’s universal genius was its equal strength in both

of the main currents of mathematics, the continuous and the discrete.” In the realm

of the discrete, he was one of the originators of number theory and made many far-

reaching contributions to this subject throughout his life. In addition, the origins

of topology—one of the dominant forces in modern mathematics—lie in his solution

of the K¨onigsberg bridge problem and his formula V − E + F = 2 connecting the

numbers of vertices, edges, and faces of a simple polyhedron.

The distinction between pure and applied mathematics did not exist in Euler’s

day, and for him the entire physical universe was a convenient object whose diverse

phenomena oﬀered scope for his methods of analysis. The foundations of classical

mechanics had been laid down by Newton, but Euler was the principal architect. In

his treatise of 1736 he was the ﬁrst to explicitly introduce the concept of a mass-

point, or particle, and he was also the ﬁrst to study the acceleration of a particle

moving along any curve and to use the notion of a vector in connection with velocity

and acceleration. His continued successes in mathematical physics were so numerous,

and his inﬂuence was so pervasive, that most of his discoveries are not credited to

him at all and are taken for granted in the physics community as part of the natural

order of things. However, we do have Euler’s angles for the rotation of a rigid body,

and the all-important Euler–Lagrange equation of variational dynamics.

11.1.3 The Error Function

The error function, used extensively in statistics, is deﬁned as

erf(x)=

√

−x

−t

dt =

√

−t

dt (11.9)

and has the property that erf(∞) = 1. The error function erf(x)givesthe

area under the bell-shaped (normal) probability distribution located between

−x and +x.

11.1.4 Elliptic Functions

Recall from calculus

that the element of length of a curve parameterized by

x = f(t),y= g(t),z= h(t),t

≤ t ≤ t

Or from our discussion of the parametric equation of curves in Chapter 4.

11.1 Integrals as Functions 323

in Cartesian coordinates is

dl =



+ dy

+ dz





(t)]

+[g



(t)]

+[h



(t)]

dt,

where prime indicates the derivative. So, the length L of the curve connecting

the initial point (f(t

),g(t

),h(t

)) to the ﬁnal point (f(t

),g(t

),h(t

)) is

L =





(t)]

+[g



(t)]

+[h



(t)]

dt. (11.10)

The length of many curves, some very complicated-looking, can be found

there is no formula

in closed form for

the circumference

of an ellipse!

analytically using Equation (11.10). However, that of a simple curve such

as an ellipse turns out to be impossible! Let us see what we get when we

try to calculate the circumference of an ellipse. The parametric equation of

an ellipse of respective semi-major and semi-minor axes a and b lying in the

xy-plane is conveniently written as

x = a sin t, y = b cos t, z =0, 0 ≤ t ≤ 2π. (11.11)

Substitution of these equations in (11.10) yields

L =

2π



[a cos t]

+[−b sin t]

+[0]

dt =

2π



cos

t + b

sin

tdt

2π



(1 −sin

t)+b

sin

tdt = a

2π



1 − k

sin

tdt, (11.12)

where k

=(a

− b

)/a

. This innocent-looking integral does not succumb

to any technique of integration. It was this resistance to analytical solution

that prompted the nineteenth century mathematicians to study this and other

related integrals as functions in their own right.

The elliptic integral of the ﬁrst kind is deﬁned as

elliptic integral of

the ﬁrst kind

F (ϕ, k) ≡



1 − k

sin

(11.13)

with F a function of two variables because the integral involves two parame-

ters, one appearing in the integrand and the other appearing as a limit.

The elliptic integral of the second kind is deﬁned as

elliptic integral of

the second kind

E(ϕ, k) ≡



1 − k

sin

tdt. (11.14)

The elliptic integral of the second kind can be interpreted as the length of

partial arcs of an ellipse. The circumference L of an ellipse with respective

semi-major and semi-minor axes a and b is simply

L = aE(2π, k)wherek =

√

− b

324 Integrals and Series as Functions

It is common to deﬁne the complete elliptic integral of the ﬁrst and

second kinds:

complete elliptic

integrals

K(k) ≡ F





π/2



1 − k

sin

E(k) ≡ E





π/2



1 − k

sin

tdt. (11.15)

The reader may easily verify (Problem 11.10) that the total circumference of

an ellipse can be given in terms of complete elliptic integrals.

The parameterization given in Equation (11.11) is that of a horizontal

ellipse (a>b). However, one may wish to start with a vertical ellipse (a<b).

Then, as the reader may verify, one ends up with an integral similar to (11.14),

except that the coeﬃcient of sin

t is +k

. Would this be a new elliptic

integral? Problem 11.9 shows that the new integral can be written as a sum

of the existing elliptic integrals.

Example 11.1.2.

Elliptic integrals show up in areas of physics totally unrelated

to the circumference of an ellipse. Consider a pendulum of mass m and length llarge-angle

pendulum and

elliptic integrals

displacedbyanangleθ from its equilibrium position as shown in Figure 11.1. When

the angle is θ, the velocity of the pendulum is l

θ and its height is h. Conservation

of energy leads to

E = KE + PE =

m(l

θ)

+ mgh =

+ mg(l − l cos θ),

where E is the total mechanical energy of the pendulum. If θ

is the maximum

angular displacement, then the total energy at this angle will be just the potential

energy.

It then follows that

m(l

θ)

+ mgh =

+ mg(l − l cos θ)=mg(l − l cos θ

or, after dividing both sides by ml,

− g cos θ = −g cos θ

. (11.16)

Figure 11.1: The pendulum displaced by an arbitrary angle θ.

The KE is zero at θ

because the pendulum comes to a momentary stop there.

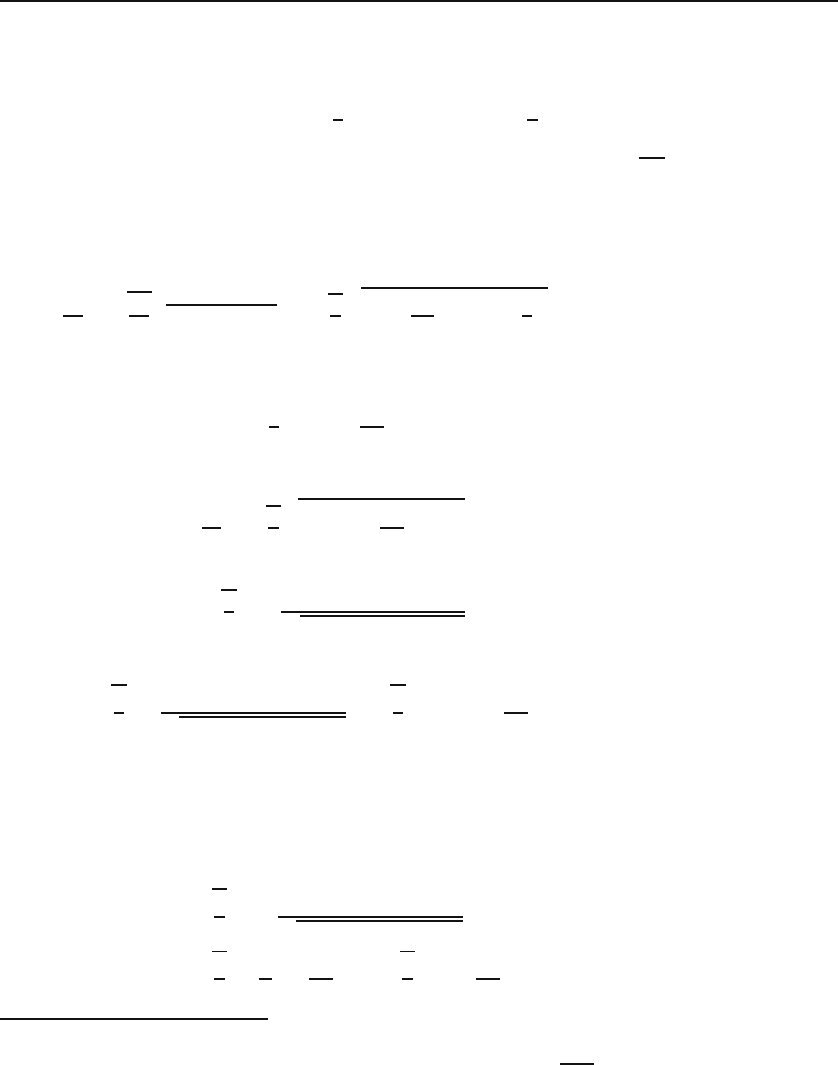
11.1 Integrals as Functions 325

The elementary treatment of the pendulum problem diﬀerentiates Equation

(11.16) with respect to time, assumes that the maximum angle—and therefore any

angle—is small, and approximates sin θ with θ in radians. This leads to

θ + gl

θ sin θ =0 or

θ +

sin θ =0

θ→0

−→

θ +

θ =0,

which is the equation of a simple harmonic oscillator

with ω

= g/l or T =2π



l/g.

This is the famous result—known even to Galileo—that, for small angles, the period

of oscillation is independent of the angle.

A more advanced treatment makes no approximation for the angle and simply

integrates (11.16). Assuming that

θ>0, Equation (11.16) gives

dθ



√

cos θ − cos θ



sin





− sin





, (11.17)

where we used the trigonometric identity cos θ =1−2sin

(θ/2). Introducing a new

variable s given by

sin





≡ sin





sin s,

diﬀerentiating this equation with respect to t, and using Equation (11.17) yields



1 − sin





sin

s. (11.18)

This leads to



dt =



1 − sin

(θ

/2) sin

which can be integrated to yield

t =



1 − sin

(θ

/2) sin

≡



s(θ), sin



, (11.19)

where s =sin

−1

[sin(θ/2)/ sin(θ

/2)], and we have assumed that at t = 0, the angle

θ is zero and therefore s = 0 as well.

Of particular interest is the period of the oscillation which is four times the time period of a

pendulum depends

on the amplitude

of oscillation.

it takes the pendulum to go from θ =0toθ = θ

. These values correspond to s =0

and s = π/2. It follows that

T =4

π/2



1 − sin

(θ

/2) sin

≡ 4



, sin





sin



. (11.20)

Recall that the equation of a simple harmonic oscillator (SHO)—such as a spring–mass

system with mass m and spring constant k—is m¨x + kx =0or¨x +(k/m)x =0. Itisshown

in elementary physics that the angular frequency of this SHO is ω =



k/m.Thus,in

any SHO equation in which the second derivative appears with no coeﬃcient, the coeﬃcient

of the undiﬀerentiated quantity is the square of the angular frequency.

326 Integrals and Series as Functions

This shows clearly that for large maximum angles, the period does depend on the

amplitude. By expanding the integrand in a power series as developed in Chapter

10, one can obtain the deviation from constant period as powers of sin

(θ

/2). We

quote the result of such an expansion

T =2π



sin

+ ···



. (11.21)

The reader is urged to verify this result (see Problems 11.11 and 11.12).



Historical Notes

The study of elliptical integrals can be said to have started in 1655 when Wallis

began to study the arc length of an ellipse. In fact he considered the arc lengths of

various cycloids and related these arc lengths to that of the ellipse. Both Wallis and

Newton published an inﬁnite series expansion for the arc length of the ellipse.

In 1679 Jacob Bernoulli attempted to ﬁnd the arc length of a spiral and encoun-

tered an example of an elliptic integral. He made an important step in the theory

of elliptic integrals in 1694. He examined the shape that an elastic rod will take if

compressed at the ends. He showed that the curve could be expressed in terms of

an integral, which was very similar to the one obtained by Wallis.

There is no doubt that Gauss obtained a number of key results in the theory

of elliptic functions, because many of these were found after his death in papers he

had never published. However, the acknowledged founders of the theory of elliptic

functions were Abel and Jacobi.

Niels Henrik Abel was the son of a poor pastor. As a student in Christiania

(Oslo), Norway, he had the luck to have Berndt Holmb¨oe (1795–1850) as a teacher.

Holmb¨oe recognized Abel’s genius and predicted when Abel was seventeen that he

would become the greatest mathematician in the world. After studying at Christia-

nia and at Copenhagen, Abel received a scholarship that permitted him to travel.

In Paris, he was presented to Legendre, Laplace,andCauchy, but they ignored him.

Having exhausted his funds, he departed for Berlin and spent the years 1825–1827

with Crelle.

He returned to Christiania so exhausted that he found it necessary, he wrote, to

hold on to the gates of a church. To earn money he gave lessons to young students.

Niels Henrik Abel

1802–1829

He began to receive attention through his published works, and Crelle thought he

might be able to secure him a professorship at the University of Berlin. But Abel

became ill with tuberculosis and died in 1829 when he was only twenty-seven years

old.

Abel knew of the work of Euler, Lagrange,andLegendre on elliptic integrals, and

may have gotten ideas for his own work from the work of Gauss. Abel started to

write papers in 1825. He presented his major paper to the Academy of Sciences in

Paris in 1826. The paper was given to Cauchy to review it. But partly because of the

length and the diﬃculty of the paper and partly to favor his own work, Cauchy laid

it aside. After Abel’s death, when his fame was established, the academy searched

for the paper, found it, and published it in 1841.

The other discoverer of elliptic functions was Carl Gustav Jacob Jacobi.

Unlike Abel, he lived a quiet life. Born in Potsdam to a Jewish family, he studied at