Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


10.5 Multipole Expansion 297
is indeterminate. Using Equation (10.30) yields
lim
x→0
ln[h(x)] = lim
x→0
1/x
−1/x
2
= lim
x→0
(−x)=0.
Therefore, lim
x→0
h(x)=e
0
= 1. So, we have the interesting result lim
x→0
x
x
=1.
The limit of x
2
/(1 − cos x)asx goes to zero is obtained as follows:
lim
x→0
x
2
1 − cos x
= lim
x→0
2x
sin x
= lim
x→0
2
cos x
=2.
Here we had to differentiate twice because the ratio of the first derivatives was also
indeterminate.
It is instructive for the reader to verify all limits in Example 10.4.1 using
L’Hˆopital’s rule to appreciate the ease of the Taylor expansion method.
10.5 Multipole Expansion
One extremely useful application of the power series representation of func-
tions is in potential theory. The electrostatic or gravitational potential can
be written as
Φ(r)=K
##
Ω
dQ(r
)
|r − r
|
, (10.31)
where K is k
e
for electrostatics and −G for gravity. Similarly, Q represents
either electric charge or mass. In some applications, especially for electrostatic
potential, the distance of the field point P from the origin is much larger than
the distance of the source point P
from the origin. This means that r>>r
and we can expand in the powers of the ratio r
/r whichwedenoteby.The
key to this expansion is a power series expansion of 1/|r − r
|. First write
1
|r − r
|
=
1
√
r
2
+ r
2
− 2r · r
=
1
r
√
1+
2
− 2
ˆ
e
r
·
ˆ
e
r
=
1
r
1+
2
− 2
ˆ
e
r
·
ˆ
e
r
!
−1/2
.
Next use the binomial expansion (10.15) with x =
2
−2
ˆ
e
r
·
ˆ
e
r
and α = −
1
2
.
Up to second order in , this yields
1
|r − r
|
=
1
r
3
1 −
1
2
2
− 2
ˆ
e
r
·
ˆ
e
r
!
+
3
8
2
− 2
ˆ
e
r
·
ˆ
e
r
!
2
+ ···
4
=
1
r
,
1+
ˆ
e
r
·
ˆ
e
r
+
2
.
−
1
2
+
3
2
(
ˆ
e
r
·
ˆ
e
r
)
2
/
+ ···
-
=
1
r
+
ˆ
e
r
·r
r
2
+
r
2
r
3
.
−
1
2
+
3
2
(
ˆ
e
r
·
ˆ
e
r
)
2
/
+ ··· . (10.32)

298 Application of Common Series
Substituting this in Equation (10.31), we obtain
Φ(r)=
K
r
##
Ω
dQ(r
)+
K
r
2
ˆ
e
r
·
##
Ω
r
dQ(r
)
+
K
r
3
##
Ω
r
2
.
−
1
2
+
3
2
(
ˆ
e
r
·
ˆ
e
r
)
2
/
dQ(r
)+··· (10.33)
=
KQ
r
+
K
r
2
ˆ
e
r
· p
Q
+
K
r
3
##
Ω
r
2
.
−
1
2
+
3
2
(
ˆ
e
r
·
ˆ
e
r
)
2
/
dQ(r
)+··· ,
where
Q ≡
##
Ω
dQ(r
)
is the total Q (charge, or mass)—also called the zeroth Q moment—and
electric dipole
moment defined
p
Q
≡
##
Ω
r
dQ(r
) (10.34)
is the first Q moment, which in the case of charge is also called the electric
dipole moment. One can also define higher moments.
If the source of the potential is discrete, the integral in Equation (10.31)
becomes a sum. The steps leading to (10.33) will not change except for switch-
ing all the integrals to summations. In particular, the dipole moment of N
point sources { Q
k
}
N
k=1
, located at {r
k
}
N
k=1
, turns out to be
p
Q
=
N
k=1
Q
k
r
k
. (10.35)
For the special case of two electric charges q
1
=+q and q
2
= −q,weobtain
3
p = qr
1
− qr
2
= q(r
1
− r
2
). (10.36)
Thus, the dipole moment of a pair of equal charges of opposite sign is the
magnitude of the charge times the displacement vector from the negative to
the positive charge.
Example 10.5.1.
Electric dipoles are fairly abundant in Nature. For example,
an antenna is approximated as a dipole at distances far away from it; and in atomic
transitions one uses the so-called dipole approximation to calculate the rate ofdipole
approximation transition and the lifetime of a state.
Let us write the explicit form of the potential of a dipole, i.e., the second term on
the RHS of Equation (10.33). In Cartesian coordinates, in which the dipole moment
is in the z-direction (so that p = p
ˆ
e
z
), the potential can be written as
3
It is customary to denote the electric dipole moment by p with no subscript.

10.6 Fourier Series 299
Φ
dip
(x, y, z)=
k
e
r
2
ˆ
e
r
· p =
k
e
r
3
r · p =
k
e
pz
(x
2
+ y
2
+ z
2
)
3/2
.
More important is the expression for potential in spherical coordinates: electric potential
of a dipole
Φ
dip
(r, θ, ϕ)=
k
e
p
r
2
cos θ
ˆ
e
r
·
ˆ
e
z
=
k
e
p
r
2
cos θ. (10.37)
The azimuthal symmetry (independence of ϕ) comes about because we chose p to
lie along the z-axis.
10.6 Fourier Series
Power series are special cases of the series of functions in which the nth func-
tion is (x − a)
n
—or simply x
n
—multiplied by a constant. These functions,
simple and powerful as they are, cannot be used in all physical applica-
tions. More general functions are needed for many problems in theoretical
physics.
The most widely used series of functions in applications are Fourier series
in which the functions are sines and cosines. These are especially suitable for
periodic functions which repeat themselves with a certain period. Suppose
periodic functions
that a function f(x) is defined in the interval (a, b). Can we write it as a
series in sines and cosines, as we did in terms of orthogonal polynomials [see
Theorem 7.5.2]? Let L = b −a denote the length of the interval, and consider
the functions
sin
2nπx
L
, cos
2nπx
L
.
Let us try the series expansion
Fourier series
expansion
f(x)=a
0
+
∞
n=1
a
n
cos
2nπx
L
+ b
n
sin
2nπx
L
, (10.38)
where we have separated the n = 0 term. Now the sine and cosine terms have
the following easily obtainable useful properties:
#
b
a
sin
2nπx
L
dx =
#
b
a
cos
2nπx
L
dx =
#
b
a
sin
2nπx
L
cos
2mπx
L
dx =0,
#
b
a
sin
2nπx
L
sin
2mπx
L
dx =
0
0ifm = n,
L/2ifm = n =0,
(10.39)
#
b
a
cos
2nπx
L
cos
2mπx
L
dx =
0
0ifm = n,
L/2ifm = n =0.
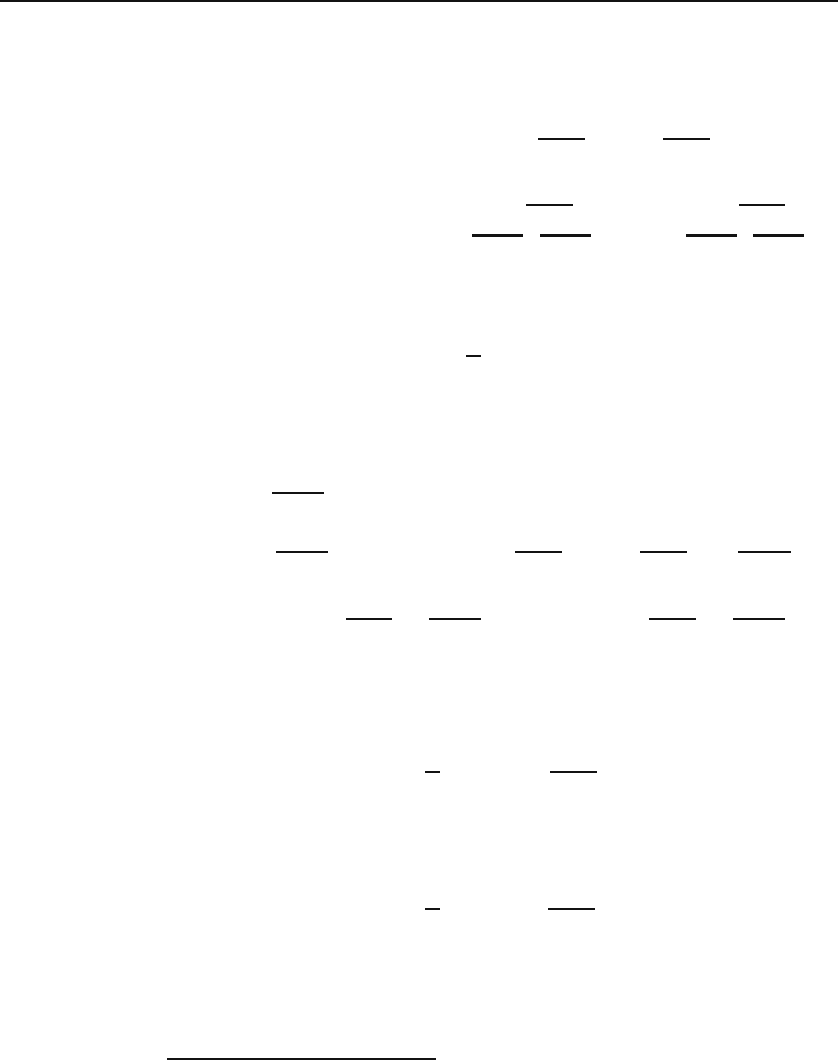
300 Application of Common Series
These properties suggest a way of determining the coefficients of the seriesexpansion of
periodic functions
in terms of Fourier
series
for a given function as in the case of orthogonal polynomials. If we integrate
both sides of Equation (10.38) from a to b,weget
4
#
b
a
f(x) dx = a
0
#
b
a
dx +
#
b
a
∞
n=1
a
n
cos
2nπx
L
+ b
n
sin
2nπx
L
dx
=(b −a)a
0
+
∞
n=1
a
n
#
b
a
cos
2nπx
L
dx
=0
+
∞
n=1
b
n
#
b
a
sin
2nπx
L
dx
=0
or
b
a
f(x) dx = a
0
L. This yields
a
0
=
1
L
#
b
a
f(x) dx. (10.40)
Multiplying Equation (10.38) by cos(2mπx/L) and integrating both sides from
a to b,weobtain
#
b
a
f(x)cos
2mπx
L
dx
= a
0
#
b
a
cos
2mπx
L
dx +
#
b
a
∞
n=1
a
n
cos
2nπx
L
+ b
n
sin
2nπx
L
cos
2mπx
L
dx
=0+
∞
n=1
a
n
#
b
a
cos
2nπx
L
cos
2mπx
L
dx +
∞
n=1
b
n
#
b
a
sin
2nπx
L
cos
2mπx
L
dx
= a
m
L/2,
where we used Equation (10.39). This yields
a
n
=
2
L
#
b
a
f(x)cos
2nπx
L
dx. (10.41)
Similarly, multiplying both sides of Equation (10.38) by sin(2mπx/L)and
integrating from a to b, yields
b
n
=
2
L
#
b
a
f(x)sin
2nπx
L
dx. (10.42)
Equations (10.38), (10.40), (10.41), and (10.42) provide a procedure for
representing a function f(x) as a Fourier series. However, the RHS of Equation
(10.38) is periodic. This means that for values of x outside the interval (a, b),
f(x) is also periodic. In fact, from Equation (10.38), we have
Fourier series
always represents
aperiodic
function.
4
Here we are assuming that the series converges uniformly so that we can switch the
order of integration and summation. This assumption turns out to be correct, but we shall
forego its (difficult) proof.
10.6 Fourier Series 301
f(x + L)=a
0
+
∞
n=1
(
a
n
cos
2nπ(x + L)
L
+ b
n
sin
2nπ(x + L)
L
)
= a
0
+
∞
n=1
(
a
n
cos
2nπx
L
+2nπ
+ b
n
sin
2nπx
L
+2nπ
)
= a
0
+
∞
n=1
a
n
cos
2nπx
L
+ b
n
sin
2nπx
L
= f(x).
Thus, f(x) repeats itself at the end of each interval of length L, i.e., it is pe-
riodic with period L. Fourier series is especially suited for representing such
functions. In fact, any periodic function has a Fourier series expansion, and
the simplicity of sine and cosine functions makes this expansion particularly
useful in applications such as electrical engineering and acoustics where peri-
odic functions in the form of waves and voltages are daily occurrences. Let
us look at some examples.
5
Example 10.6.1. In the study of electrical circuitry, periodic voltage signals of
different shapes are encountered. An example is the so-called square wave of height
V
0
, and duration and “rest duration” T [see Figure 10.3(top)]. The potential as a
function of time, V (t), can be expanded as a Fourier series. The interval is (0, 2T ), square wave
potentialbecause that is one whole cycle of potential variation. We thus write
V (t)=a
0
+
∞
n=1
a
n
cos
2nπt
2T
+ b
n
sin
2nπt
2T
(10.43)
1 2 3 4 5 6
–0.2
0.2
0.4
0.6
0.8
1
1 2 3 4 5 6
–0.2
0.2
0.4
0.6
0.8
1
Figure 10.3: Top: The periodic square-wave potential with V
0
=1and T =2.
Bottom: Various approximations to the Fourier series of the square-wave potential. The
dashed plot is that of the first term of the series, the thick gray plot keeps 3 terms, and
the solid plot 15 terms.
5
While Taylor series expansion demands that the function be (infinitely) differentiable,
the orthogonal polynomial and Fourier series expansion require only piecewise continuity.
This means that the function can have any (finite) number of discontinuities in the interval
(a, b). Thus, the expanded function can not only be nondifferentiable, it can even be
discontinuous.
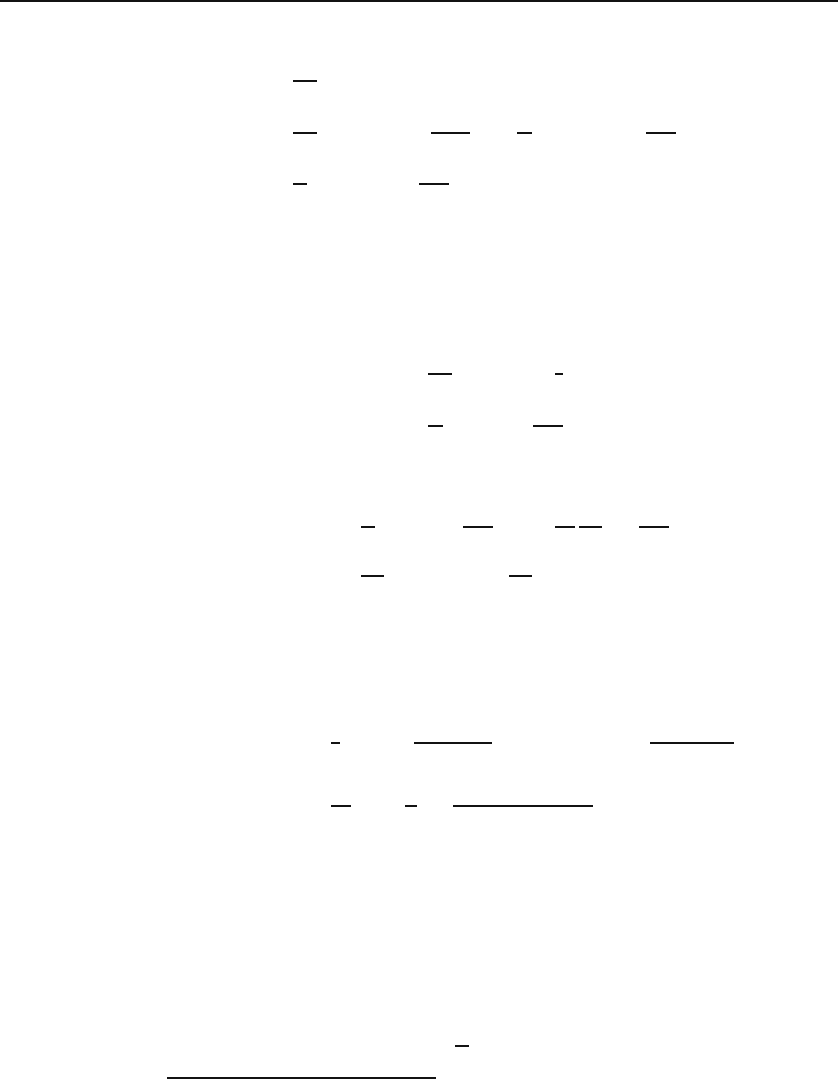
302 Application of Common Series
with
a
0
=
1
2T
#
2T
0
V (t) dt,
a
n
=
2
2T
#
2T
0
V (t)cos
2nπt
2T
dt =
1
T
#
2T
0
V (t)cos
nπt
T
dt, (10.44)
b
n
=
1
T
#
2T
0
V (t)sin
nπt
T
dt.
Substituting
V (t)=
0
V
0
if 0 ≤ t ≤ T,
0ifT<t≤ 2T,
in Equation (10.44), we obtain
a
0
=
1
2T
#
T
0
V
0
dt =
1
2
V
0
,
a
n
=
1
T
#
T
0
V
0
cos
nπt
T
dt =0,
and
b
n
=
1
T
#
T
0
V
0
sin
nπt
T
dt = −
V
0
T
T
nπ
cos
nπt
T
T
0
=
V
0
nπ
(1 − cos nπ)=
V
0
nπ
[1 − (−1)
n
] .
Thus, there is no contribution from the cosine sum, and in the sine sum only the
odd terms contribute (b
n
=0ifn is even). Therefore, let n =2k +1, where k now
takes all values even and odd, and substitute all the above information in Equation
(10.43), to obtain
V (t)=
1
2
V
0
+
∞
k=0
V
0
(2k +1)π
*
1 − (−1)
2k+1
+
sin
(2k +1)πt
T
=
V
0
2
0
1+
4
π
∞
k=0
sin[(2k +1)πt/T]
2k +1
1
.
The plots of the sum truncated at the first, third, and fifteenth terms are shown
in Figure 10.3(bottom). Note how the Fourier approximation overshoots the value
of the function at discontinuities. This is a general feature of all discontinuous
functions and is called the Gibb’s phenomenon.
6
Gibb’s
phenomenon
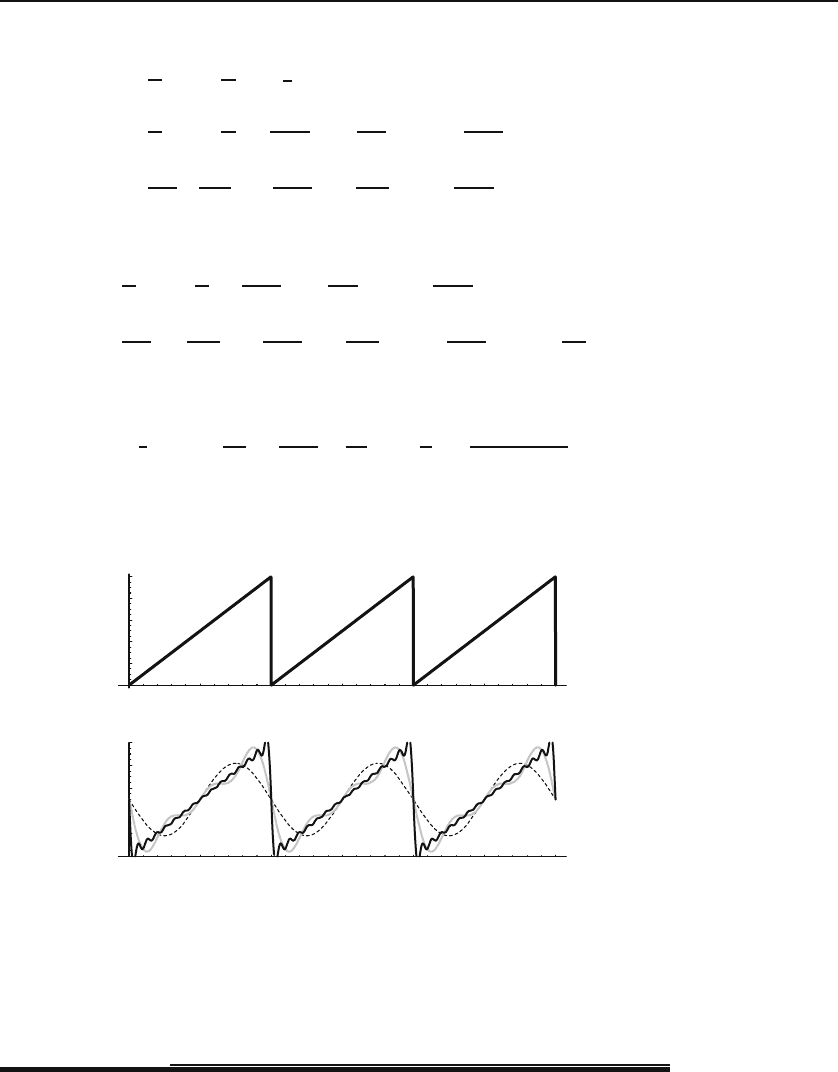
Example 10.6.2. Another frequently used potential is the sawtooth potential.
sawtooth potential
The interval is (0,T) and the equation for the potential is
V (t)=V
0
t
T
for 0 ≤ t<T.
6
A discussion of Gibb’s phenomenon can be found in Hassani, S. Mathematical Physics:
A Modern Introduction to Its Foundations, Springer-Verlag, 1999, Chapter 8.
10.6 Fourier Series 303
The coefficients of expansion can be obtained as usual:
a
0
=
1
T
#
T
0
V
0
t
T
dt =
1
2
V
0
,
a
n
=
2
T
#
T
0
V
0
t
T
cos
2nπt
T
dt =
2V
0
T
2
#
T
0
t cos
2nπt
T
dt
=
2V
0
T
2
0
T
2nπ
t sin
2nπt
T
T
0
−
T
2nπ
#
T
0
sin
2nπt
T
dt
1
=0,
and
b
n
=
2
T
#
T
0
V
0
t
T
sin
2nπt
T
dt =
2V
0
T
2
#
T
0
t sin
2nπt
T
dt
=
2V
0
T
2
0
−
T
2nπ
t cos
2nπt
T
T
0
+
T
2nπ
#
T
0
cos
2nπt
T
dt
1
= −
V
0
nπ
.
Substituting the coefficients in the sum, we get
V (t)=
1
2
V
0
−
∞
n=1
V
0
nπ
sin
2nπt
T
=
V
0
2
0
1 −
2
π
∞
n=1
sin(2nπt/T )
n
1
.
The plot of the sawtooth wave as well as those of the sum truncated at the first,
third, and fifteenth term are shown in Figure 10.4.
123456
0.2
0.4
0.6
0.8
1
123456
0.2
0.4
0.6
0.8
1
Figure 10.4: Top: The periodic sawtooth potential with V
0
=1and T =2. Bottom:
Various approximations to the Fourier series of the sawtooth potential. The dashed plot
is that of the first term of the series, the thick gray plot keeps 3 terms, and the solid
plot 15 terms.
Historical Notes
Although Euler made use of the trigonometric series as early as 1729, and d’Alembert
considered the problem of the expansion of the reciprocal of the distance between

304 Application of Common Series
two planets in a series of cosines of the multiples of the angle between the rays from
the origin to the two planets, it was Fourier who gave a systematic account of the
trigonometric series.
Joseph Fourier did very well as a young student of mathematics but had set
his heart on becoming an army officer. Denied a commission because he was the son“The profound
study of nature is
the most fruitful
source of
mathematical
discoveries.”
Joseph Fourier
of a tailor, he went to a Benedictine school with the hope that he could continue
studying mathematics at its seminary in Paris. The French Revolution changed
those plans and set the stage for many of the personal circumstances of Fourier’s
later years, due in part to his courageous defense of some of its victims, an action
that led to his arrest in 1794. He was released later that year, and he enrolled
as a student in the Ecole Normale, which opened and closed within a year. His
performance there, however, was enough to earn him a position as assistant lec-
turer (under Lagrange and Monge)intheEcole Polytechnique. He was an excellent
mathematical physicist, was a friend of Napoleon, and accompanied him in 1798 to
Egypt, where Fourier held various diplomatic and administrative posts while also
conducting research. Napoleon took note of his accomplishments and, on Fourier’s
return to France in 1801, appointed him prefect of the district of Is`ere, in south-
eastern France, and in this capacity built the first real road from Grenoble to Turin.
He also befriended the boy Champollion, who later deciphered the Rosetta stone
as the first long step toward understanding the hieroglyphic writing of the ancient
Egyptians.
Joseph Fourier
1768–1830
Like other scientists of his time, Fourier took up the flow of heat. The flow was
of interest as a practical problem in the handling of metals in industry and as a
scientific problem in attempts to determine the temperature at the interior of the
Earth, the variation of that temperature with time, and other such questions. He
submitted a basic paper on heat conduction to the Academy of Sciences of Paris
in 1807. The paper was judged by Lagrange, Laplace,andLegendre,andwasnot
published, mainly due to the objections of Lagrange, who had earlier rejected the
use of trigonometric series. But the Academy did wish to encourage Fourier to
develop his ideas, and so made the problem of the propagation of heat the subject
of a grand prize to be awarded in 1812. Fourier submitted a revised paper in 1811,
which was judged by the men already mentioned, and others. It won the prize but
was criticized for its lack of rigor and so was not published at that time in the
M´emoires of the Academy.
He developed a mastery of clear notation, some of which is still in use today. (The
placement of the limits of integration near the top and bottom of the integral sign was
introduced by Fourier.) It was also his habit to maintain close association between
mathematical relations and physically measurable quantities, especially in limiting
or asymptotic cases, even performing some of the experiments himself. He was
one of the first to begin full incorporation of physical constants into his equations,
and made considerable strides toward the modern ideas of units and dimensional
analysis.
Fourier continued to work on the subject of heat and, in 1822, published one of
the classics of mathematics, Th´eorie Analytique de la Chaleur, in which he made
extensive use of the series that now bears his name and incorporated the first part
of his 1811 paper practically without change. Two years later he became secretary
of the Academy and was able to have his 1811 paper published in its original form
in the M´emoires.

10.7 Multivariable Taylor Series 305
10.7 Multivariable Taylor Series
The approximation to which we alluded at the beginning of this chapter is
just as important when we are dealing with functions depending on several
variables as those depending on a single variable. After all, most functions
encountered in physics depend on space coordinates and time. We begin with
two variables because the generalization to several variables will be trivial
once we understand the two-variable case.
A direct—and obvious—generalization of the power series to the case of a
function f(u, v) of two variables about the point (u
0
,v
0
)gives
f(u, v)=a
00
+ a
10
(u − u
0
)+a
01
(v − v
0
)+a
20
(u −u
0
)
2
+ a
02
(v − v
0
)
2
+ a
11
(u − u
0
)(v − v
0
)+a
30
(u −u
0
)
3
+ a
21
(u − u
0
)
2
(v − v
0
)+a
12
(u − u
0
)(v − v
0
)
2
+ a
03
(v − v
0
)
3
+ ··· . (10.45)
The notation used above needs some explanation. All the a’s are constants
with two indices such that the first index indicates the power of (u −u
0
)and
the second that of (v − v
0
). To obtain a Taylor series, we need to relate a’s
to derivatives of f . This is straightforward: To find a
kj
, differentiate both
sides of Equation (10.45) k times with respect to u and j times with respect
to v and evaluate the result at (u
0
,v
0
). Thus, to evaluate a
00
, we differentiate
zero times with respect to u and zero times with respect to v and substitute
u
0
for u and v
0
for v on both sides. We then obtain
f(u
0
,v
0
)=a
00
+0+0+···+0+···= a
00
.
By differentiating with respect to u and evaluating both sides at (u
0
,v
0
), we
obtain
∂
1
f(u
0
,v
0
)=0+a
10
+0+···+0+···= a
10
.
Similarly,
∂
2
f(u
0
,v
0
)=0+0+a
01
+0+···+0+···= a
01
,
∂
1
∂
1
f(u
0
,v
0
)=∂
2
1
f(u
0
,v
0
)=2a
20
,
∂
2
∂
2
f(u
0
,v
0
)=∂
2
2
f(u
0
,v
0
)=2a
02
,
∂
2
∂
1
f(u
0
,v
0
)=a
11
.
We want to write Equation (10.45) in a succinct form to be able to extract
a general formula for the coefficients. An inspection of that equation suggests
that
f(u, v)=
∞
j=0
∞
k=0
a
jk
(u − u
0
)
j
(v − v
0
)
k
.

306 Application of Common Series
It is more useful to collect terms of equal total power together. Thus, writing
m = k + j, and noting that j cannot be larger than m, we rewrite the above
equation as
f(u, v)=
∞
m=0
m
j=0
a
j,m−j
(u − u
0
)
j
(v − v
0
)
m−j
.
Let us introduce the notation ∂
k,n−k
for k differentiations with respect to the
first variable, and n − k differentiations with respect to the second:
7
∂
k,n−k
f ≡
∂
n
f
∂u
k
∂v
n−k
and apply it to both sides of the sum above. Evaluating the result at (u
0
,v
0
),
we obtain
∂
k,n−k
f(u
0
,v
0
)=
∞
m=0
m
j=0
a
j,m−j
∂
k,n−k
,
(u −u
0
)
j
(v − v
0
)
m−j
-
(u
0
,v
0
)
.
If j<kor m −j<n− k then the corresponding terms differentiate to zero.
On the other hand, if j>kor m − j>n− k then some powers of u −u
0
or
v − v
0
will survive and evaluation at (u
0
,v
0
) will also give zero. So, the only
term in the sum that survives the differentiation is the term with j = k and
m − j = n − k which gives k!(n − k)!. We thus have
Taylor series of a
function of two
variables
∂
k,n−k
f(u
0
,v
0
)=k!(n −k)!a
k,n−k
⇒ a
k,n−k
=
∂
k,n−k
f(u
0
,v
0
)
k!(n − k)!
,
and the Taylor series can finally be written as
f(u, v)=
∞
n=0
n
k=0
∂
k,n−k
f(u
0
,v
0
)
k!(n −k)!
(u − u
0
)
k
(v − v
0
)
n−k
. (10.46)
Sometimes this is written in terms of increments to suggest approximation as
in the single-variable case:
f(u +Δu, v +Δv)=
∞
n=0
n
k=0
∂
k,n−k
f(u, v)
k!(n − k)!
(Δu)
k
(Δv)
n−k
, (10.47)
where we used (u, v) instead of (u
0
,v
0
). Once again, the first term in the
expansion is f(u, v) and the rest is a correction.
The three-dimensional formula should now be easy to construct. We write
Taylor series of a
function of three
variables
this as
8
f(u, v, w)=
∞
n=0
i+j+k=n
∂
n
ijk
f(u
0
,v
0
,w
0
)
i!j!k!
(u−u
0
)
i
(v−v
0
)
j
(w−w
0
)
k
. (10.48)
7
This notation is not universal. Sometimes ∂
n
kj
is used with the understanding that
k + j = n.
8
The symbol ∂
n
ijk
represents the nth derivative with i differentiations with respect to the
first variable, j differentiations with respect to the second variable, and k differentiations
with respect to the third variable, such that i + j + k = n.
