Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

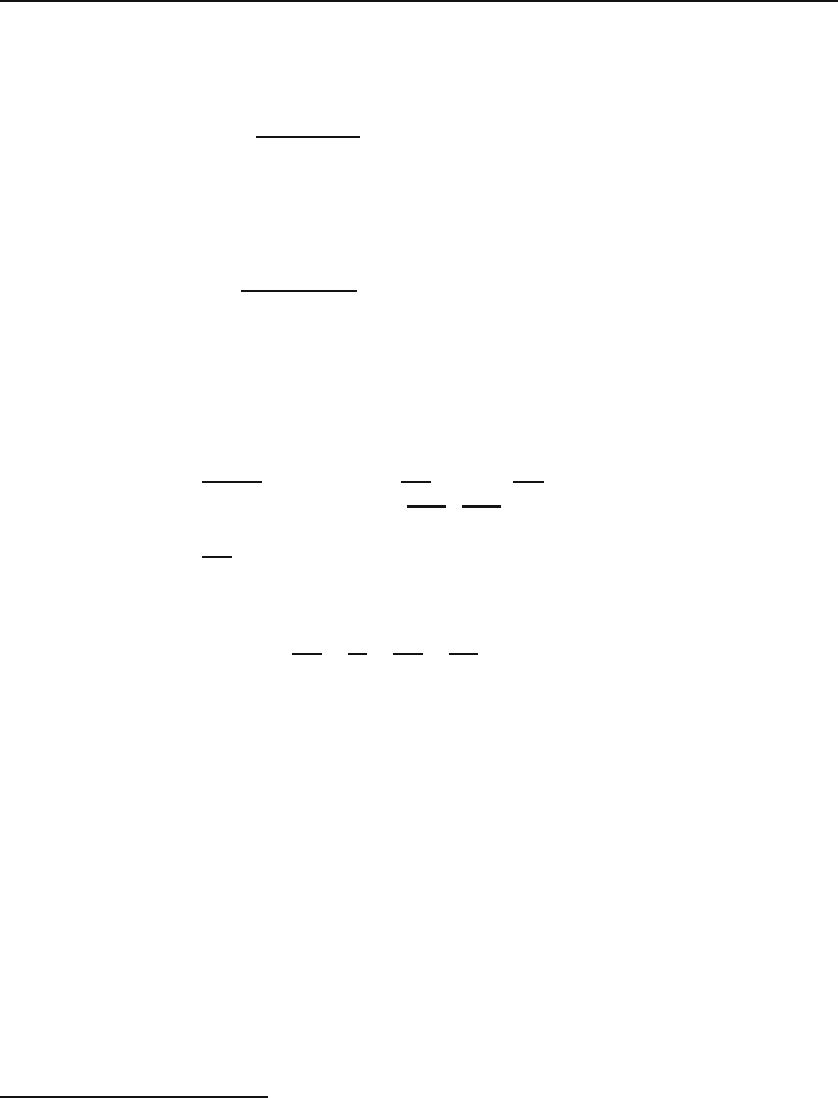
10.8 Application to Differential Equations 307
For a given value of n, suggested by the outer sum, the inner sum describes a
procedure whereby all terms whose i, j,andk indices add up to n are grouped
together. As a comparison, we also write Equation (10.46) in this notation:
f(u, v)=
∞
n=0
j+k=n
∂
n
jk
f(u
0
,v
0
)
j!k!
(u −u
0
)
j
(v − v
0
)
k
. (10.49)
The three-dimensional Taylor series in terms of increments becomes
f(u +Δu, v +Δv, w +Δw)
=
∞
n=0
i+j+k=n
∂
n
ijk
f(u, v, w)
i!j!k!
(Δu)
i
(Δv)
j
(Δw)
k
, (10.50)
where again (u
0
,v
0
,w
0
) has been replaced by (u, v, w).
Example 10.7.1.
As an example we expand e
x
sin y about the origin.
9
Using the
notation in Equation (10.49), the coefficients, within a factor of j!k!, can be written
as
∂
n
jk
(e
x
sin y)
(0,0)
=
∂
n
∂x
j
∂y
k
(e
x
sin y)
(0,0)
=
∂
j
∂x
j
(e
x
)
x=0
=1
∂
k
∂y
k
(sin y)
y=0
=
∂
k
∂y
k
(sin y)
y=0
.
The first few terms of the Taylor expansion of this function can now be written
down:
e
x
sin y = y + xy +
x
2
y
2
−
y
3
6
−
xy
3
6
+
x
3
y
6
+ ··· .
One could also obtain this result by multiplying the Taylor expansions of e
x
and
sin y term by term.
10.8 Application to Differential Equations
One of the most powerful methods of solving an ordinary differential equation
(ODE) is the power series method, and we shall use this method to solve some
of the most recurring differential equations of mathematical physics in Chap-
ters 25 through 27. Power series are uniformly and absolutely convergent, and
can be differentiated term by term. This makes them a good candidate for
representing the (unknown) solutions of differential equations. The relation
among the derivatives, expressed in a differential equation, becomes a relation
among coefficients of the power series, the so-called recursion relation,which
is enough to determine all the relevant coefficients of the series, leaving only
those coefficients which require initial conditions for their determination. The
best way to understand the method is to look at an example.
9
The use of x and y in place of u and v should not cause any confusion.

308 Application of Common Series
Example 10.8.1. The differential equation
dx
dt
= bx
can be assumed to have a power series solution of the form
x(t)=
∞
n=0
c
n
t
n
.
This power series will be uniformly and absolutely convergent for some interval
on the real line, and as such, can be differentiated. Differentiating the foregoing
equation and substituting the result in the differential equation, we get
∞
n=1
nc
n
t
n−1
= b
∞
n=0
c
n
t
n
.
The essential property of power series is the equality of the corresponding coefficients
when two such series are equal (see Theorem 10.1.4). Before using this property in
the above equation, however, we need to reexpress the LHS so that the power of t
is the same on both sides. We thus change the dummy index from n to m = n − 1,
so that all n’s are replaced by m +1. Wethenget
LHS =
∞
m+1=1
(m +1)c
m+1
t
m
=
∞
m=0
(m +1)c
m+1
t
m
.
Since we are free to use any dummy index we please, let us change m to n so that
we can compare the two sides of the equation. This gives
∞
n=0
(n +1)c
n+1
t
n
=
∞
n=0
bc
n
t
n
⇒ (n +1)c
n+1
= bc
n
. (10.51)
We can immediately test for the convergence of the series using the ratio test:
lim
n→∞
c
n+1
t
n+1
c
n
t
n
= lim
n→∞
tbc
n
/(n +1)
c
n
= lim
n→∞
bt
n +1
=0
for all b and t. Thus, regardless of the value of b and t, the series converges.
We have established the convergence of the series representation of the solution
of our differential equation. We now have to find the coefficients. This is done by
rewriting Equation (10.51) as
c
n+1
=
b
n +1
c
n
(10.52)
which is called the recursion relation of the series. By iterating this relation werecursion relation
can obtain all the coefficients in terms of the first one as follows:
c
n+1
=
b
n +1
c
n
=
b
n +1
b
n
c
n−1
=
b
2
(n +1)n
c
n−1
=
b
2
(n +1)n
b
n − 1
c
n−2
=
b
3
(n +1)n(n − 1)
c
n−2
.

10.8 Application to Differential Equations 309
Since we are interested in finding c
n
,wecanrewritethisequationas
c
n
=
b
3
n(n − 1)(n − 2)
c
n−3
,
where we have lowered all n’s on both sides by one unit. This relation can easily be
generalized to an arbitrary positive integer j:
c
n
=
b
j
n(n − 1) ···(n − j +1)
c
n−j
.
In particular, if we set j = n,weobtain
c
n
=
b
n
n(n − 1) ···2 · 1
c
0
=
b
n
n!
c
0
(10.53)
which upon substitution in the original series, yields
x(t)=
∞
n=0
c
0
b
n
n!
t
n
= c
0
∞
n=0
(bt)
n
n!
= c
0
e
bt
,
where we have used Equation (10.12). The unknown c
0
is determined by the value
of x(t)atagivent, usually t =0.
There are of course much easier ways of solving the simple differential
equation above, and the method used may appear to “kill a fly with a sledge-
hammer.” Nevertheless, it illustrates the almost mechanical way of obtaining
the solution without resorting to any “tricks” used so often in arriving at the
closed-form solutions of differential equations.
Example 10.8.2.
Let us look at another familiar example. The motion of a mass
m driven by a spring with spring constant k is governed by the differential equation
m
d
2
x
dt
2
= −kx ⇒
d
2
x
dt
2
+
k
m
x =0.
Once again we assume a solution of the form
x(t)=
∞
n=0
a
n
t
n
= a
0
+ a
1
t + a
2
t
2
+ ···+ a
n
t
n
+ ···
and differentiate it twice to get
dx
dt
=
∞
n=1
na
n
t
n−1
= a
1
+2a
2
t + ···+ na
n
t
n−1
+ ···,
d
2
x
dt
2
=
∞
n=2
n(n − 1)a
n
t
n−2
=2a
2
+3· 2a
3
t + ···+ n(n − 1)a
n
t
n−2
+ ··· .
Substitute j = n −2tobringthepoweroft into a form that can be compared with
the RHS. This amounts to substituting j +2forall n’s:
d
2
x
dt
2
=
∞
j=0
(j +2)(j +1)a
j+2
t
j
=
∞
n=0
(n +2)(n +1)a
n+2
t
n
.
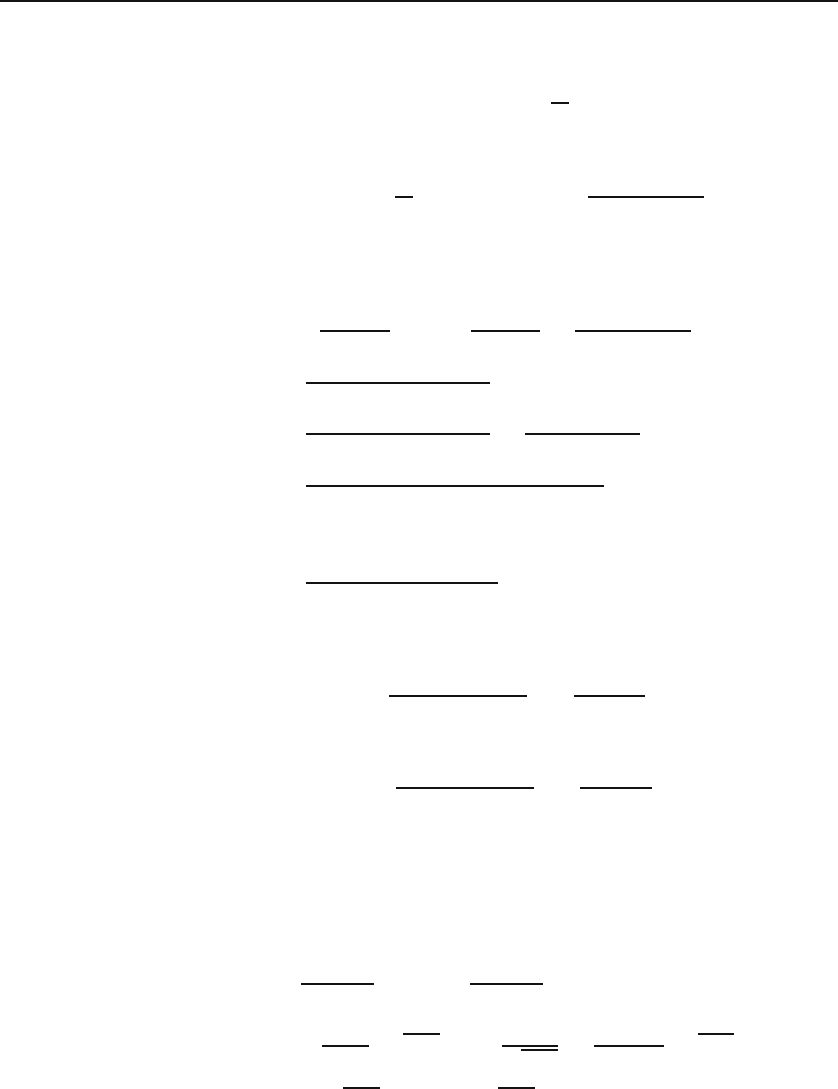
310 Application of Common Series
In the last step we simply changed the dummy index. Substituting this and the
series for x(t) in the differential equation, we obtain
∞
n=0
(n +2)(n +1)a
n+2
t
n
+
k
m
∞
n=0
a
n
t
n
=0
which gives the recursion relation
(n +2)(n +1)a
n+2
+
k
m
a
n
=0 ⇒ a
n+2
= −
k/m
(n +2)(n +1)
a
n
. (10.54)
Application of the ratio test [as given by Equation (9.10) with j = 2] immediately
yields that the series is convergent for all values of k/m and all values of t.Ifwe
lower the value of n by two units on both sides, we get
a
n
= −
k/m
n(n − 1)
a
n−2
= −
k/m
n(n − 1)
(
−
k/m
(n − 2)(n − 3)
a
n−4
)
=
(−k/m)
2
n(n − 1)(n −2)(n − 3)
a
n−4
=
(−k/m)
2
n(n − 1)(n −2)(n − 3)
(
−
k/m
(n − 4)(n −5)
a
n−6
)
=
(−k/m)
3
n(n − 1)(n −2)(n − 3)(n − 4)(n − 5)
a
n−6
.
.
.
=
(−k/m)
i
n(n − 1) ···(n − 2i +1)
a
n−2i
,
where i is some positive integer. Because of the form of this equation, we should
consider two cases: For even n,weleti = n/2orn =2i to obtain
a
2i
=
(−k/m)
i
2i(2i − 1) ···2 · 1
a
0
=
(−k/m)
i
(2i)!
a
0
and for odd n we let i =(n − 1)/2orn =2i +1toget
a
2i+1
=
(−k/m)
i
(2i +1)2i ···2 · 1
a
1
=
(−k/m)
i
(2i +1)!
a
1
.
Thus all even coefficients are given in terms of a
0
,andalloddonesintermsofa
1
.
Absolute convergence of the series now allows us to rearrange terms and separate
even and odd terms to write
x(t)=
∞
n=even
a
n
t
n
+
∞
n=odd
a
n
t
n
=
∞
j=0
a
2j
t
2j
+
∞
j=0
a
2j+1
t
2j+1
=
∞
j=0
(−k/m)
j
(2j)!
a
0
t
2j
+
∞
j=0
(−k/m)
j
(2j +1)!
a
1
t
2j+1
= a
0
∞
j=0
(−1)
j
(2j)!
k/m t
2j
+
a
1
k/m
∞
j=0
(−1)
j
(2j +1)!
k/m t
2j+1
= A cos
k/m t
+ B sin
k/m t
,

10.9 Problems 311
where A = a
0
and B = a
1
/
k/m are arbitrary constants to be determined by the
initial conditions of the problem. The Maclaurin series for sine and cosine used
above are given in Equations (10.13) and (10.14).
The examples above, although illustrating the utility of the power series
method of solving differential equations, should not give the impression that
one needs no other methods. The closed-form solutions are sometimes essen-
tial for interpreting the physical properties of the system under consideration.
For example, if the mass of the preceding example is in a fluid, so that a
damping force retards the motion, the closed-form solution will turn out to
be
x(t)=Ae
−γt
cos(ωt + α),ω≡
k
m
,
where γ is the damping factor and α is an arbitrary phase. Deciphering this
damping factor
closed form from its power series expansion, obtained by solving the differ-
ential equation by the series method, is next to impossible. The closed-form
solution shows clearly, for instance, how the amplitude of the oscillation de-
creases with time, an information that may not be evident from the series
solution of the problem. Nevertheless, on many occasions, a closed-form so-
lution may not be available, in which case the power series solution will be
the only alternative. In fact, many of the functions of mathematical physics
were invented in the last century as the power series solutions of differential
equations.
10.9 Problems
10.1. Write the first five terms of the expansion of the binomial function
(10.15) for (a) α =
3
2
,(b)α =
1
3
,and(c)α =
3
4
.
10.2. Find the rational number of which each of the following decimal num-
bers is a representation:
(a) 0.5555 .... (b) 0.676767 .... (c) 0.123123 ....
(d) 1.1111 .... (e) 2.727272 .... (f) 1.108108 ....
10.3. Find the interval of convergence of the Maclaurin series for each of the
familiar functions discussed in Section 10.2.
10.4. Using the series representation of the familiar functions evaluate the
following series:
(a)
∞
k=1
(−1)
k
x
2k+1
2k
. (b)
∞
k=0
x
2k+1
(2k)!
. (c)
∞
k=0
x
k+1
(k+1)!
.
(d)
∞
n=1
(−1)
n−1
x
3n−2
n3
n
. (e)
∞
n=0
(−1)
n+2
x
3n+1
3
3n+1
(2n)!
. (f)
∞
m=0
x
m+1
(2m+1)!
.
10.5. Derive Equation (10.17).

312 Application of Common Series
10.6. Use the Maclaurin series to find the limits of the following ratios as
x → 0:
2
√
1 − x
2
+ x
2
− 2
2cosx − 2+x
2
,
sin x − ln(1 + x)
e
x
− x − cos x
.
10.7. (a) Use the Maclaurin series expansion up to x
3
to find the following
limit:
lim
x→0
2
3
√
1 − 6x − 2cosx +4sinx +7x
2
ln(1 −x)+e
x
− 1
.
(b) Use the Maclaurin series expansion up to x
4
to find the following limit:
lim
x→0
e
x
− ln(1 + x
2
) −cos x +sinx − 2x
2
√
4+x
2
+cosx − 5
.
10.8. In the special theory of relativity the energy E of a particle of mass m
and speed v is given by
E =
mc
2
1 − (v/c)
2
,
where c is the speed of light. Show that for ordinary speeds (v<<c), one
obtains the classical expression for the kinetic energy, defined to be E minus
the rest energy.
10.9. The gravitational potential energy for a particle of mass m at a distance
r from the center of a planet of radius R and mass M is given by
Φ(r)=−
GMm
r
+ C, r > R.
(a) Find C so that the potential at the surface of the planet is zero.
(b) Show that at a height h<<Rabove the surface of the planet, the potential
energy can be written as mgh.Findg in terms of M and R and calculate
the numerical value of g for the Earth, the Moon, and Jupiter. Look up the
data you need in a table usually found in introductory physics or astronomy
books.
10.10. Prove the hyperbolic identities of Equation (10.21).
10.11. Show that
sech
2
x =1−tanh
2
x, cosech
2
x =coth
2
x − 1,
and
d
dx
tanh x =sech
2
x,
d
dx
coth x = −cosech
2
x.
10.12. Derive Equation (10.23).

10.9 Problems 313
10.13. Use L’Hˆopital’s rule to obtain the following limits:
(a) lim
x→0
(2+x)ln(1−x)
(1−e
x
)cosx
. (b) lim
x→∞
x ln
x+1
x−1
.
(c) lim
x→a
3
√
x−
3
√
a
x−a
. (d) lim
x→0
xe
x
1−e
x
.
(e) lim
x→
1
2
π
(tan x)
cos x
. (f) lim
x→0
(ln x)tanx.
10.14. Use L’Hˆopital’s rule to obtain the limits of Example 10.4.1.
10.15. Show that the following sequences converge and find their limits:
ln n
n
p
,
n
2
2
n
,nln
1+
1
n
,P(n) e
−n
,
where p is a positive number and P (n) is a polynomial in n.
10.16. The Yukawa potential of a charge distribution is given by
Φ(r)=
##
Ω
k
e
e
−κ|r−r
|
dq(r
)
|r − r
|
,
where κ is a constant. By expanding |r −r
| up to the first order in r
/r,show
that
Φ(r) ≈
k
e
Qe
−κr
r
+
k
e
(κr +1)e
−κr
r
2
ˆ
e
r
·p,
where p is the dipole moment of the charge distribution.
10.17. A conic surface has an opening angle of 2α and a lateral length a as
shown in Figure 10.5. It carries a uniform charge density σ.
(a) Show that the electrostatic potential Φ at a distance r from the vertex on
the axis of the cone is
Φ(r)=2πk
e
σ sin α
r
2
+ a
2
− 2ar cos α − r
+(2πk
e
σ sin α cos α)r ln
a −r cos α +
√
r
2
+ a
2
− 2ar cos α
r − r cos α
.
α
a
Figure 10.5: The cone of Problem 10.17.
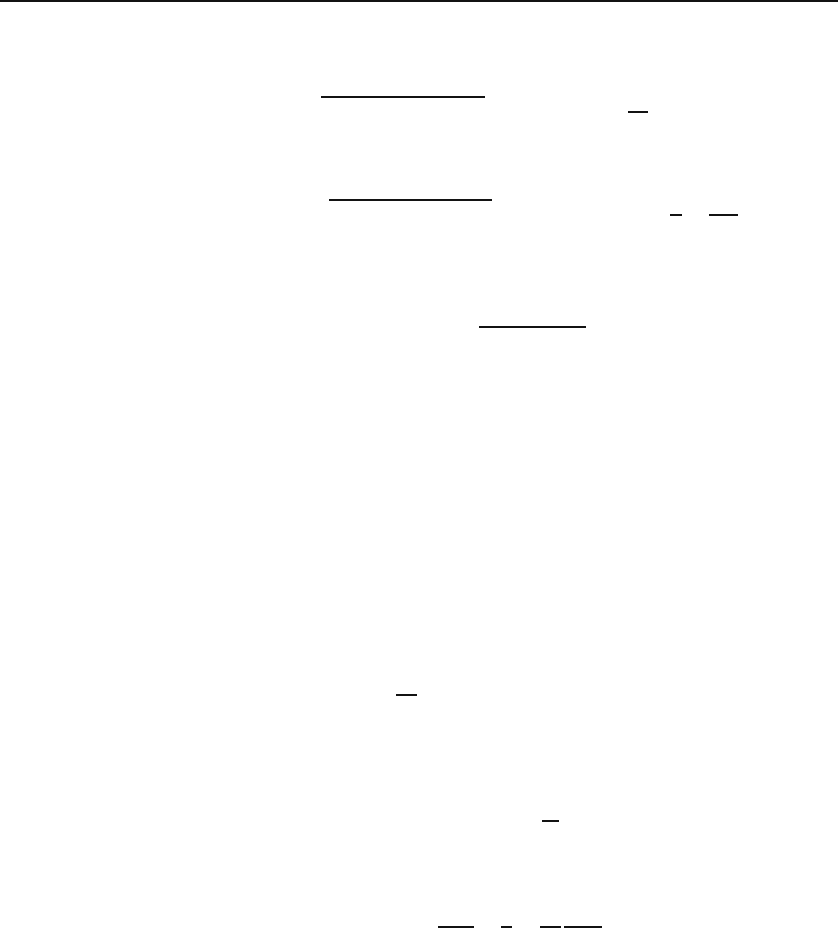
314 Application of Common Series
(b) Now suppose that r a, expand the square roots and the log up to the
second power of the ratio a/r,andshowthat
r
2
+ a
2
− 2ar cos α ≈ r − a cos α +
a
2
2r
sin
2
α
and
ln
a −r cos α +
r
2
+ a
2
− 2ar cos α
≈ ln |r −r cos α|+
a
r
+
a
2
2r
2
(1 + cos α).
(c) Put (a) and (b) together to show that the potential can be approximated
by
Φ(r) ≈
πk
e
σa
2
sin α
r
.
Write this expression in terms of the total charge in the cone. Do you get
what you expect?
10.18. Recall from your introductory physics courses that the electric field at
adistanceρ from a long uniformly charged rod has only a radial component
which is given by E = λ/2π
0
ρ,whereλ is the linear charge density. Show
this result by setting a = −L/2 (why?) and taking the limit of infinite L in
Equation (4.13).
10.19. After calculating the potentials of Problems 4.11 and 4.12 for finite
L, find their limits when L →∞.
10.20. The potential of a certain charge distribution with total charge Q is
given by
Φ=
k
e
a
0
#
[ln |r −r
|−ln b] dq(r
),
where k
e
, a
0
,andb are constants.
(a) Show that for r
r, one can use the approximation
ln |r −r
|≈ln r −
r
r
ˆ
e
r
·
ˆ
e
r
.
(b) Use (a) to show that the multipole expansion of Φ only up to the dipole
moment is
Φ ≈
k
e
Q
a
0
ln
r
b
−
k
e
a
0
p · r
r
2
.
10.21. Find the dipole moment of a uniformly charged sphere about its center.
10.22. A voltage is given by the graph shown in Figure 10.6.
(a) Write the function V (t) describing the voltage for 0 ≤ t ≤ 2T .
(b) If this voltage repeats itself periodically, find the Fourier series expansion
of V (t).

10.9 Problems 315
T
2T
V
0
t
V(t)
Figure 10.6: The voltage of Problem 10.22.
10.23. A periodic voltage with period 2T is given by
V (t)=
0
V
0
cos(πt/T)if− T/2 ≤ t ≤ T/2,
0ifT/2 ≤|t|≤T.
(a) Sketch this function for the interval −3T ≤ t ≤ 3T .
(b) Find a
0
and a
1
, the first two cosine coefficients of the Fourier series ex-
pansion of V (t).
(c) Find a
n
and all b
n
, the sine coefficients.
(d) Write down the Fourier series of V (t). Evaluate both sides at t =0to
show that
π
2
=1−2
∞
n=1
(−1)
n
4n
2
− 1
.
This is one of the many series representations of π.
10.24. An electric voltage V (t)isgivenby
V (t)=V
0
sin
πt
2T
, 0 ≤ t ≤ T
and repeats itself with period T .
(a) Sketch V (t) for values of t from t =0tot =3T .
(b) Find the Fourier series expansion of V (t).
10.25. A periodic voltage is given by the formula
V (t)=
0
V
0
sin(πt/2T )if0≤ t ≤ T,
0ifT ≤ t ≤ 2T.
(a) Sketch the voltage for the interval (−4T,4T ).
(b) Find the Fourier series representation of this voltage.
10.26. A periodic voltage with period 4T is given by
V (t)=
⎧
⎨
⎩
V
0
1 −
t
2
T
2
if − T ≤ t ≤ T
0ifT ≤|t|≤2T.

316 Application of Common Series
(a) Sketch this function for the interval −6T ≤ t ≤ 6T .
(b) Find a
0
, a
n
,andb
n
, the coefficients of the Fourier series expansion of
V (t).
(c) Write down the Fourier series of V (t).
(d) Evaluate both sides at t = T . Do you obtain an identity? If not, what
sort of relationship is obtained if we demand the equality of both sides?
10.27. Write out Equation (10.50) up to the second power in the Δ’s.
10.28. Find the Taylor series expansion of e
x
ln(1 + y)about(0, 0).
10.29. (a) Find the multivariable Taylor series expansion of e
xy
about (0, 0).
(b) Now let z = xy, expand the function e
z
, and substitute xy for z in the
expansion. Show that the results of (a) and (b) agree.
10.30. Determine all the solutions of the differential equation
dx
dt
+2tx =0
using infinite power series. From the power series solution guess the closed-
form solution. Now suppose that x(0) = 1. What is the specific solution with
this property?
10.31. Consider the differential equation
dx
dt
+3t
2
x =0.
(a) Use a solution of the form
∞
n=0
a
n
t
n
and find a
1
and a
2
.
(b) Find a recursion relation relating coefficients.
(c) From the recursion relation determine the radius of convergence of the
infinite series.
(d) Find all coefficients in terms of only one.
(e) Guess the closed-form solution from the series. Now suppose that x(0) = 2.
What is the specific solution with this property? What is the numerical value
of x(−2)?
