Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


10.2 Series for Some Familiar Functions 287
all powers of Δx. The smaller the increment, the smaller the number of terms
of the correction we need to keep to achieve a given accuracy.
A convenient value for a is 0, in which case the series is called Maclaurin
series:
f(x)=f(0) +
f
(0)
1!
x + ···=
∞
k=0
f
(k)
(0)
k!
x
k
. (10.11)
10.2 Series for Some Familiar Functions
In this subsection, we give the Maclaurin series representation of a few familiar
functions. These representations are so useful that the reader is urged to
commit them to memory.
The Exponential Function
For e
x
, the derivatives of all orders are e
x
implying that f
(n)
(0) = 1 for all n.
Therefore,
Maclaurin series of
exponential
function
e
x
=1+
x
1!
+
x
2
2!
+ ···=
∞
n=0
x
n
n!
. (10.12)
This series converges uniformly for all x as we saw in Example 10.1.2.
The Trigonometric Functions
The sine function has the following derivatives:
Maclaurin series of
trigonometric
function
f
(x)=cosx, f
(x)=−sin x, f
(x)=−cos x, f
(iv)
(x)=sinx, ....
This can be summarized as
f
(n)
(x)=
0
(−1)
n/2
sin x if n is even,
(−1)
(n−1)/2
cos x if n is odd.
Evaluating at x = 0 for the Maclaurin series yields
f
(n)
(0) =
0
0ifn is even,
(−1)
(n−1)/2
if n is odd,
so that
sin x =0+x −0 −
x
3
3!
+0+
x
5
5!
−···=
∞
k=0
(−1)
k
x
2k+1
(2k +1)!
. (10.13)
The combination 2k + 1 ensures that only odd terms are included even though
there is no restriction on the sum over k. The radius of convergence is
r
∗
= lim
k→∞
(−1)
k
/(2k +1)!
(−1)
k+1
/(2k +3)!
= lim
k→∞
(2k +3)!
(2k +1)!
= ∞.

288 Application of Common Series
Thus the Taylor series representation of the sine function is convergent for
all x.
The Maclaurin series representation of the cosine function can be obtained
similarly. We leave the details to the reader, and simply quote the result:
cos x =
∞
k=0
(−1)
k
x
2k
(2k)!
, −∞ <x<∞. (10.14)
The Binomial Function
Another useful function which is used extensively in physics is the binomial
function with arbitrary exponent, i.e., (1 + x)
α
with α an arbitrary real num-
ber. It is easy to find the nth derivative of this function:
f
(n)
(x)=α(α −1)(α − 2) ···(α − n + 1)(1 + x)
α−n
,n≥ 1.
Evaluating this at x =0gives
c
n
=
f
(n)
(0)
n!
=
α(α −1) ···(α −n +1)
n!
,n≥ 1.
From this, we can immediately find the radius of convergence:
r
∗
= lim
n→∞
c
n
c
n+1
= lim
n→∞
α(α − 1) ···(α −n +1)
n!
·
(n +1)!
α(α −1) ···(α −n)
= lim
n→∞
n +1
α −n
=1.
Thus, the series is convergent for −1 <x<1, and we can write
Maclaurin series of
binomial function
(1 + x)
α
=1+
∞
n=1
α(α − 1) ···(α −n +1)
n!
x
n
, −1 <x<1. (10.15)
Example 10.2.1.
Because of the frequent occurrence of the square root, we work
through the calculation of (10.15) for α = ±
1
2
.Forα =+
1
2
,wehave
√
1+x =(1+x)
1/2
=1+
∞
n=1
1
2
(
1
2
− 1) ···(
1
2
− n +1)
n!
x
n
=1+
1
2
x +
∞
n=2
(−1)
n−1
1 · 3 · 5 ···(2n − 3)
2
n
n!
x
n
.
Now let n = m + 1 and rewrite the sum as
√
1+x =1+
1
2
x +
∞
m=1
(−1)
m
1 · 3 ·5 ···(2m − 1)
2
m+1
(m +1)!
x
m+1
=1+
1
2
x −
1
8
x
2
+
3
48
x
3
−···. (10.16)

10.2 Series for Some Familiar Functions 289
Thecaseofα = −
1
2
can be handled in exactly the same way. We simply quote
the result
1
√
1+x
=1+
∞
m=1
(−1)
m
1 · 3 · 5 ···(2m − 1)
2
m
m!
x
m
=1−
1
2
x +
3
8
x
2
−
15
48
x
3
··· , (10.17)
and urge the reader to fill in the details.
It is important to note the limitations of the power series representation
of a function: Although (1 + x)
α
is defined for all positive
1
values of x,the
power series representation of it is good only for a limited region of the real
line.
In many applications, the binomial function appears in the form (u + v)
α
where |v| < |u| and one is interested in the power series expansion in v/u.
This is easily done:
(u + v)
α
=
3
u
1+
v
u
4
α
= u
α
1+
v
u
α
= u
α
+ u
α
∞
n=1
α(α −1) ···(α −n +1)
n!
v
u
n
(10.18)
= u
α
+
∞
n=1
α(α − 1) ···(α −n +1)
n!
u
α−n
v
n
, −|u| <v<|u|.
In practice, v is usually much smaller than u, and the requirement of conver-
gence is overwhelmingly met.
The Hyperbolic Functions
The exponential function and the trigonometric functions have very similar
power series: Except for (the crucial) coefficient (−1)
k
,sinx appears to be
the odd part of the expansion of e
x
and cos x its even part. The (−1)
k
factor
makes the trigonometric functions periodic. What if we take this factor away,
and simply collect the even powers of e
x
together and do the same to the
odd powers? The resulting series will of course be (absolutely and uniformly)
convergent because the exponential is so. So, let us introduce the following
functions:
Maclaurin series of
hyperbolic
functions
sinh x ≡
∞
k=0
x
2k+1
(2k +1)!
= x +
x
3
3!
+
x
5
5!
+ ··· ,
cosh x ≡
∞
k=0
x
2k
(2k)!
=1+
x
2
2!
+
x
4
4!
+ ··· , (10.19)
1
It is really defined for more than just positive values. For instance, if α is an integer,
the function is defined for all values of x. For fractional powers such as α =1/2, 1 + x
cannot be negative, so that we must restrict the values of x to x>−1.

290 Application of Common Series
sinh x (pronounced “sinch”) is called the hyperbolic sine function. Similarly,
cosh x (pronounced “kahsh”) is called the hyperbolic cosine function. By
their very definition, we have
e
x
=coshx +sinhx.
If we change x to −x, and note that sinh x is odd and cosh x is even, we can
also write
e
−x
=cosh(−x) + sinh(−x)=coshx − sinh x.
Adding and subtracting the last two equations yields
cosh x =
e
x
+ e
−x
2
, sinh x =
e
x
− e
−x
2
. (10.20)
This is how the hyperbolic functions are usually defined. From these defini-
tions, one can obtain a host of relations for the sinh and cosh that look similar
to the relations satisfied by sine and cosine. For example, it is easy to show
that
cosh
2
x − sinh
2
x =1,
d
dx
cosh x =sinhx,
d
dx
sinh x =coshx,
cosh(x ± y)=coshx cosh y ± sinh x sinh y, (10.21)
sinh(x ±y)=sinhx cosh y ± cosh x sinh y,
cosh(2x)=cosh
2
x +sinh
2
x, sinh(2x)=2sinhx cosh x.
We give the derivation for the hyperbolic cosine of the sum, leaving the rest
of them as problems for the reader. We start with the RHS:
cosh x cosh y +sinhx sinh y
=
e
x
+ e
−x
2
e
y
+ e
−y
2
+
e
x
− e
−x
2
e
y
− e
−y
2
=
(e
x
+ e
−x
)(e
y
+ e
−y
)+(e
x
− e
−x
)(e
y
− e
−y
)
4
=
e
x+y
+ e
x−y
+ e
−x+y
+ e
−x−y
+ e
x+y
− e
x−y
− e
−x+y
+ e
−x−y
4
=
2e
x+y
+2e
−x−y
4
=
e
x+y
+ e
−x−y
2
=cosh(x + y).
We can also define the analogs of other trigonometric functions:
tanh x ≡
sinh x
cosh x
=
e
x
− e
−x
e
x
+ e
−x
, coth x ≡
cosh x
sinh x
=
e
x
+ e
−x
e
x
− e
−x
, (10.22)
sech x ≡
1
cosh x
=
2
e
x
+ e
−x
, cosech x ≡
1
sinh x
=
2
e
x
− e
−x
.
These functions have such properties as
sech
2
x =1−tanh
2
x, cosech
2
x =coth
2
x − 1,
and
d
dx
tanh x =sech
2
x,
d
dx
coth x = −cosech
2
x.

10.3 Helmholtz Coil 291
The Logarithmic Function
Finally, we state the Maclaurin series for ln(1 + x), which occurs frequently
in physics, and which the reader can verify:
Maclaurin series of
logarithmic
function
ln(1 + x)=
∞
n=1
(−1)
n+1
x
n
n
, −1 <x<1. (10.23)
10.3 Helmholtz Coil
Power series are very useful tools for approximating functions, and the closer
one gets to the point of expansion, the better the approximation. The essence
of this approximation is replacing the infinite series with a finite sum, i.e.,
approximating the function with a polynomial.
In general, to get a very good approximation, one has to retain very large
powers of the power series. So, the approximating polynomial will have to
be of a high degree. However, suppose that a function f(x) has the following
expansion
f(x)=c
0
+ c
1
(x − a)+···+ c
m
(x − a)
m
+ c
m
(x − a)
m+k
+ ··· ,
where k is a fairly large number. Then the polynomial
p(x)=c
0
+ c
1
(x − a)+···+ c
m
(x − a)
m
approximates the function very accurately because, as long as we are “close”
enough to the point of expansion a, the next term in the series will not affect
the polynomial much. In particular, if the series looks like
f(x)=c
0
+ c
k
(x − a)
k
+ ··· , (10.24)
then the constant “polynomial” c
0
is an extremely good approximation to the
function for values of x close to a.
The argument above can be used to design devices to produce physical
quantities that are constant for a fairly large values of the variable on which the
outcome of the device depends. A case in point is the Helmholtz coil,which
is used frequently in laboratory situations in which homogeneous magnetic
fields are desirable.
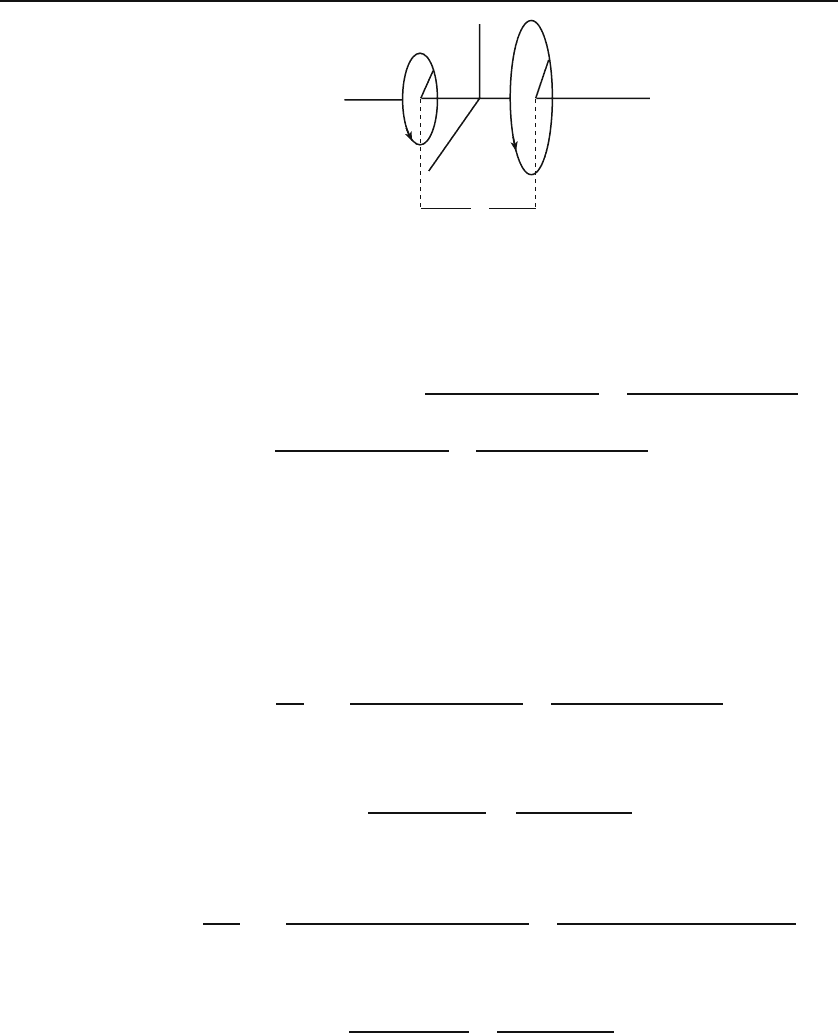
Figure 10.1 shows two loops of current-carrying wires of radii a and b
separated by a distance L. We are interested in the z-component of the
magnetic field midway between the two loops, which, to simplify expressions,
we have chosen to be the origin. Example 4.1.4 gives the expression for the
magnetic field of a loop at a point on its axis at a distance z from its center.
292 Application of Common Series
x
y
z
I
1
I
2
a
b
L
Figure 10.1: Two circular loops with different radii producing a magnetic field.
Let us denote the magnetic field of the loop of radius a by B
1
and that of the
loop of radius b by B
2
. Then Example 4.1.4 gives
B(z) ≡ B
1
(z)+B
2
(z)=
2πk
m
I
1
a
2
[a
2
+(z + L/2)
2
]
3/2
+
2πk
m
I
2
b
2
[b
2
+(z − L/2)
2
]
3/2
=
16πk
m
I
1
a
2
[4a
2
+(2z + L)
2
]
3/2
+
16πk
m
I
2
b
2
[4b
2
+(2z −L)
2
]
3/2
. (10.25)
We want to adjust the parameters of the two loops in such a way that the
magnetic field at the origin is maximally homogeneous. This can be accom-
plished by setting as many derivatives of B(z) equal to zero at the origin as
possible, so that the Maclaurin expansion of B(z) will have a maximum num-
ber of consecutive terms equal to zero, i.e., we will have an expression of the
form (10.24).
The first derivative of B(z)is
dB
dz
= −
96πk
m
I
1
a
2
(2z + L)
[4a
2
+(2z + L)
2
]
5/2
−
96πk
m
I
2
b
2
(2z − L)
[4b
2
+(2z −L)
2
]
5/2
.
Setting this equal to zero at z =0gives
I
1
a
2
(4a
2
+ L
2
)
5/2
=
I
2
b
2
(4b
2
+ L
2
)
5/2
. (10.26)
The second derivative of B(z)is
d
2
B
dz
2
= −
768πk
m
I
1
a
2
[a
2
− (2z + L)
2
]
[4a
2
+(2z + L)
2
]
7/2
−
768πk
m
I
2
b
2
[b
2
− (2z − L)
2
]
[4b
2
+(2z −L)
2
]
7/2
.
Setting this equal to zero at z =0gives
I
1
a
2
(a
2
− L
2
)
(4a
2
+ L
2
)
7/2
+
I
2
b
2
(b
2
− L
2
)
(4b
2
+ L
2
)
7/2
=0. (10.27)
Since both terms are positive, the only way that we can get zero in (10.27)
is if each term on the LHS vanishes. It follows that a = L = b. Substituting
10.3 Helmholtz Coil 293
this in Equation (10.26) gives I
1
= I
2
whichwedenotebyI. Therefore, we
can now write the magnetic field as
B(z)=16πk
m
Ia
2
(
1
[4a
2
+(2z + a)
2
]
3/2
+
1
[4a
2
+(2z −a)
2
]
3/2
)
. (10.28)
The reader may verify that not only are the first and the second derivatives
of B(z) of Equation (10.28) zero, but also its third derivative. In fact, we have
B(z)=
32πk
m
I
5
√
5a
−
4608πk
m
I
625
√
5a
5
z
4
+ ··· . (10.29)
That only even powers appear in the expansion (10.29) could have been antic-
ipated, because (10.28) is even in z as the reader may easily verify. It follows
from Equation (10.29) that B(z) should be fairly insensitive to the variation
of z at points close to the origin. Physically, this means that the magnetic
field is fairly homogeneous at the midpoint between the two loops as long as
the loops are equal and separated by a distance equal to their common radius,
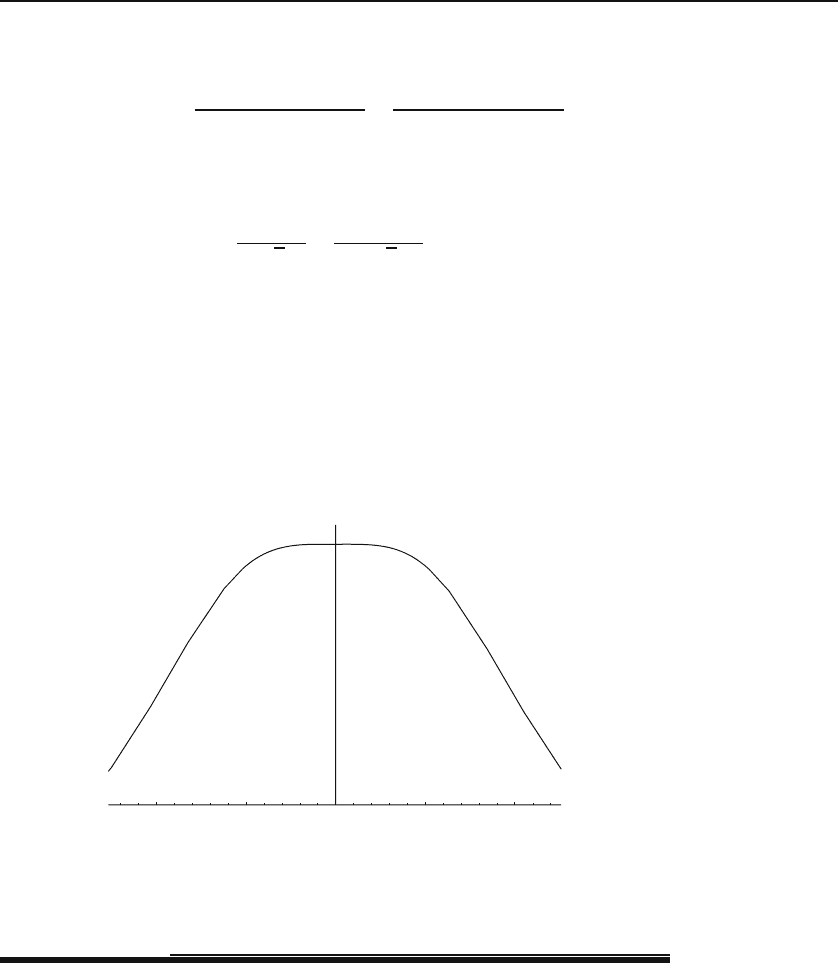
and as long as they carry the same current. Figure 10.2 shows the plot of the
magnetic field as a function of z. Note how flat the function is for even fairly
large values of z.
–1 –0.5 0.5 1
Figure 10.2: Magnetic field of a Helmholtz coil as a function of z. The horizontal axis
is z in units of a.
Historical Notes
One of the problems faced by mathematicians of the late seventeenth and early eigh-
teenth centuries was interpolation (the word was coined by Wallis)oftablesofvalues.
Greater accuracy of the interpolated values of the trigonometric, logarithmic, and
nautical tables was necessary to keep pace with progress in navigation, astronomy,
and geography. The common method of interpolation, whereby one takes the aver-
age of the two consecutive entries of a table, is called linear interpolation because
it gives the exact result for a linear function. This gives a crude approximation for

294 Application of Common Series
functions that are not linear, and mathematicians realized that a better method of
interpolation was needed.
The general method which can give interpolations that are more and more accu-
rate was given by Gregory and independently by Newton. Suppose f(x) is a function
whose values are given at a, a + h, a +2h, ..., and we are interested in the value
of the function at an x that lies between two table entries. The Gregory–Newton
formula states that
f(a + r)=f(a)+
r
h
Δf(a)+
r
h
r
h
− 1
!
2!
Δ
2
f(a)+
r
h
r
h
− 1
!
r
h
− 2
!
3!
Δ
3
f(a)+··· ,
where
Δf(a)=f(a + h) −f(a), Δ
2
f(a)=Δf(a + h) − Δf(a),
Δ
3
f(a)=Δ
2
f(a + h) − Δ
2
f(a), Δ
4
f(a)=Δ
3
f(a + h) − Δ
3
f(a),...
To calculate f at any value y between the known values, one simply substitutes y−a
for r.
Brook Taylor’s Methodus incrementorum directa et inversa, published in 1715,
added to mathematics a new branch now called the calculus of finite differences,and
he invented integration by parts. It also contained the celebrated formula known
as Taylor’s expansion, the importance of which remained unrecognized until 1772
when Lagrange proclaimed it the basic principle of the differential calculus.
Brook Taylor
1685–1731
To arrive at the series that bears his name, Taylor let h in the Gregory–Newton
formula be Δx and took the limit of smaller and smaller Δx. Thus, the third term,
for example, gave
r(r −Δx)
2!
Δ
2
f(a)
Δx
2
→
r
2
2!
f
(a)
which is the familiar third term in the Taylor series.
In 1708 Taylor produced a solution to the problem of the center of oscillation
which, since it went unpublished until 1714, resulted in a priority dispute with
Johann Bernoulli.
Taylor also devised the basic principles of perspective in Linear Perspective
(1715). Together with New Principles of Linear Perspective the first general treat-
ment of the vanishing points are given.
Taylor gives an account of an experiment to discover the law of magnetic attrac-
tion (1715) and an improved method for approximating the roots of an equation by
giving a new method for computing logarithms (1717).
Taylor was elected a Fellow of the Royal Society in 1712 and was appointed in
that year to the committee for adjudicating the claims of Newton and of Leibniz to
have invented the calculus.
10.4 Indeterminate Forms and L’Hˆopital’s Rule
It is good practice to approximate functions with their power series repre-
sentations, keeping as many terms as is necessary for a given accuracy. This
practice is especially useful when encountering indeterminate expressions of
the form
0
0
. Although L’Hˆopital’s rule (discussed below) can be used to find
the ratio, on many occasions the substitution of the series leads directly to
the answer, saving us the labor of multiple differentiation.

10.4 Indeterminate Forms and L’Hˆopital’s Rule 295
Example 10.4.1. Let us look at some examples of the ratios mentioned above.
In all cases treated in this example, the substitution x =0gives
0
0
, which is inde-
terminate. Using the Maclaurin series (10.12) and (10.13), we get
lim
x→0
2e
x
− 2 − 2x −x
2
sin x − x
= lim
x→0
2(1 + x + x
2
/2+x
3
/6+x
4
/24 + ···) − 2 − 2x −x
2
x − x
3
/6+x
5
/120 + ···−x
= lim
x→0
x
3
/3+x
4
/12 + ···
−x
3
/6+x
5
/120 −···
= lim
x→0
1/3+x/12 + ···
−1/6+x
2
/120 −···
= −2.
The series (10.14) and (10.23) can be used to evaluate the following limit:
lim
x→0
ln(1 + x) −x
cos x − 1
= lim
x→0
x − x
2
/2+x
3
/3 −···−x
1 − x
2
/2+x
4
/24 −···−1
= lim
x→0
−x
2
/2+x
3
/3 −···
−x
2
/2+x
4
/24 −···
= lim
x→0
−1/2+x/3 −···
−1/2+x
2
/24 −···
=1.
With (10.12) and (10.15), we have
lim
x→0
√
1+2x − x −1
e
x
2
− 1
= lim
x→0
1+
1
2
(2x)+
1
2
(
1
2
−1)
2!
(2x)
2
+
1
2
(
1
2
−1)(
1
2
−2)
3!
(2x)
3
+ ···−x − 1
1+x
2
+(x
2
)
2
/2! + ···−1
= lim
x→0
−x
2
/2+x
3
/2+···
x
2
+ x
4
/2+···
= lim
x→0
−1/2+x/2+···
1+x
2
/2+···
= −
1
2
.
The method of expanding the numerator and denominator of a ratio as
a Taylor series is extremely useful in applications in which mere substitution
results in the indeterminate expression
2
of the form
0
0
. However, there are
many other indeterminate forms that occur in applications. For example, a
mere substitution of x =0in(1+x)
1/x
yields 1
∞
which is also indeterminate.
Other examples of indeterminate expressions are 0×∞,
∞
∞
,0
0
,and∞
0
.Most
of these expressions can be reduced to indeterminate ratios for which one can
use l’Hˆopital’s rule:
l’Hˆopital’s rule
Box 10.4.1. (L’Hˆopital’s Rule).Iff(a)/g(a) is indeterminate, then
lim
x→a
f(x)
g(x)
= lim
x→a
f
(x)
g
(x)
, (10.30)
where f
and g
are derivatives of f and g, respectively.
2
An expression is indeterminate if it involves two parts each of which gives a result that
is contradictory to the other. Thus the numerator of the ratio
0
0
says that the ratio should
be zero, while the denominator says that the ratio should be infinite.
296 Application of Common Series
In practice, one converts the indeterminate form into a ratio and differen-
tiates the numerator and denominator as many times as necessary until one
obtains a definite result or infinity. The following general rules can be of help:
• If f(a)=0andg(a)=∞, then to find lim
x→a
f(x)g(x), rewrite the
limit as
lim
x→a
f(x)g(x) = lim
x→a
f(x)
1
g(x)
or lim
x→a
f(x)g(x) = lim
x→a
g(x)
1
f(x)
,
the first of which gives
0
0
and the second
∞
∞
. In either case, one can
apply L’Hˆopital’s rule.
• If f(a)=1andg(a)=∞, first define h(x) ≡ [f (x)]
g(x)
. Then to find
lim
x→a
h(x) = lim
x→a
[f(x)]
g(x)
,
take the natural logarithm of h(x) and convert the result into the ratio
lim
x→a
ln[h(x)] = lim
x→a
g(x)ln[f(x)] = lim
x→a
ln[f(x)]
1
g(x)
.
Then use Equation (10.30).
• If f(a)=∞ (or f(a) = 0) and g(a) = 0, then to find
lim
x→a
h(x) ≡ lim
x→a
[f(x)]
g(x)
,
take the natural logarithm of h(x) and convert the result into the ratio
lim
x→a
ln[h(x)] = lim
x→a
g(x)ln[f(x)] = lim
x→a
ln[f(x)]
1
g(x)
.
Then use Equation (10.30).
Example 10.4.2.
To find the lim
x→0
(1 + 2x)
1/x
,wewriteh(x) ≡ (1 + 2x)
1/x
and
note that
lim
x→0
ln[h(x)] = lim
x→0
(1/x)ln(1+2x) = lim
x→0
ln(1 + 2x)
x
is indeterminate. Using Equation (10.30) yields
lim
x→0
ln[h(x)] = lim
x→0
ln(1 + 2x)
x
= lim
x→0
2
1+2x
1
= lim
x→0
2
1+2x
=2.
Therefore, lim
x→0
h(x)=e
2
.
To find the lim
x→0
x
x
,wewriteh(x) ≡ x
x
and note that
lim
x→0
ln[h(x)] = lim
x→0
x ln x = lim
x→0
ln x
1/x
