Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

11.2 Power Series as Functions 327

the University of Berlin and in 1827 became a professor at K¨onigsberg. In 1842 he

had to give up his post because of ill health. He was given a pension by the Prussian

government and retired to Berlin, where he died in 1851. His fame was great even

during his lifetime, and his students spread his ideas to many centers.

Jacobi taught the subject of elliptic functions for many years. His approach be-

came the model according to which the theory of functions itself was developed. He

also worked in functional determinants (Jacobians), ordinary and partial diﬀerential

equations, dynamics, celestial mechanics, and ﬂuid dynamics.

Carl Gustav Jacobi

1804–1851

Jacobi’s work on elliptic functions started in 1827 when he submitted a paper for

publication without proof. Almost simultaneously, Abel wrote his research paper on

elliptic functions. Both had arrived at the key idea of working with inverse functions

of the elliptic integrals, an idea that Abel had had since 1823. Thereafter, they both

published on the subject. But whereas Abel died in 1829, Jacobi lived to publish

much more. In particular, his Fundamenta Nova Theoriae Functionum Ellipticarum

of 1829 became a leading work on the subject.

11.2 Power Series as Functions

Diﬀerential equations have found their way into all areas of physics from the

motion of planets around the Sun to standing waves on a rope or a drum,

to electrical properties of conductors, and the behavior of electromagnetic

ﬁelds and beyond. As is always the case, no mathematics can draw more

attention than that which deals directly with Nature. The urgency of ﬁnding

solutions to these diﬀerential equations prompted many mathematicians of the

latter part of the eighteenth and the beginning of the nineteenth centuries to

concentrate heavily on certain speciﬁc diﬀerential equations. It appeared that

every diﬀerential equation dictated by Nature gave rise to a new function. The

most common scheme for solving these diﬀerential equations was to assume

a power series solution, substitute the assumed solution in the diﬀerential

equation, and determine the (unknown) coeﬃcients from the resulting equality

of power series. We shall come back to this powerful method in Chapters 24

and 25 through 27. At this point, we want to simply give examples of solutions

(functions) of certain diﬀerential equations that were discovered in the form

of a power series.

Chapter 10 showed how known functions (such as trigonometric and log-

arithmic functions) can be represented as power series. These functions had

been known prior to the popularity of inﬁnite series, and the origin of their

discovery lay in areas of mathematics outside calculus. One does not need a

power series to calculate sin(35

◦

); an appropriate right triangle and careful

measurement of its sides and hypotenuse will do the job. The functions we are

discussing here are deﬁned in terms of power series and do not have indepen-

dent existence. With some mathematical manipulation they may be written

as a deﬁnite integral—which cannot be evaluated analytically. But that is

just as abstract as an inﬁnite series because in the latter case, the integrals

become their deﬁnition.

328 Integrals and Series as Functions

11.2.1 Hypergeometric Functions

In their studies of second-order diﬀerential equations (DE), mathematicians,

always in search of generalities, came up with the most general form of a

second-order linear DE which appeared to encompass all known DEs of phys-

ical interest. This DE, called the hypergeometric diﬀerential equation,

hypergeometric

diﬀerential

equation

turned out to be

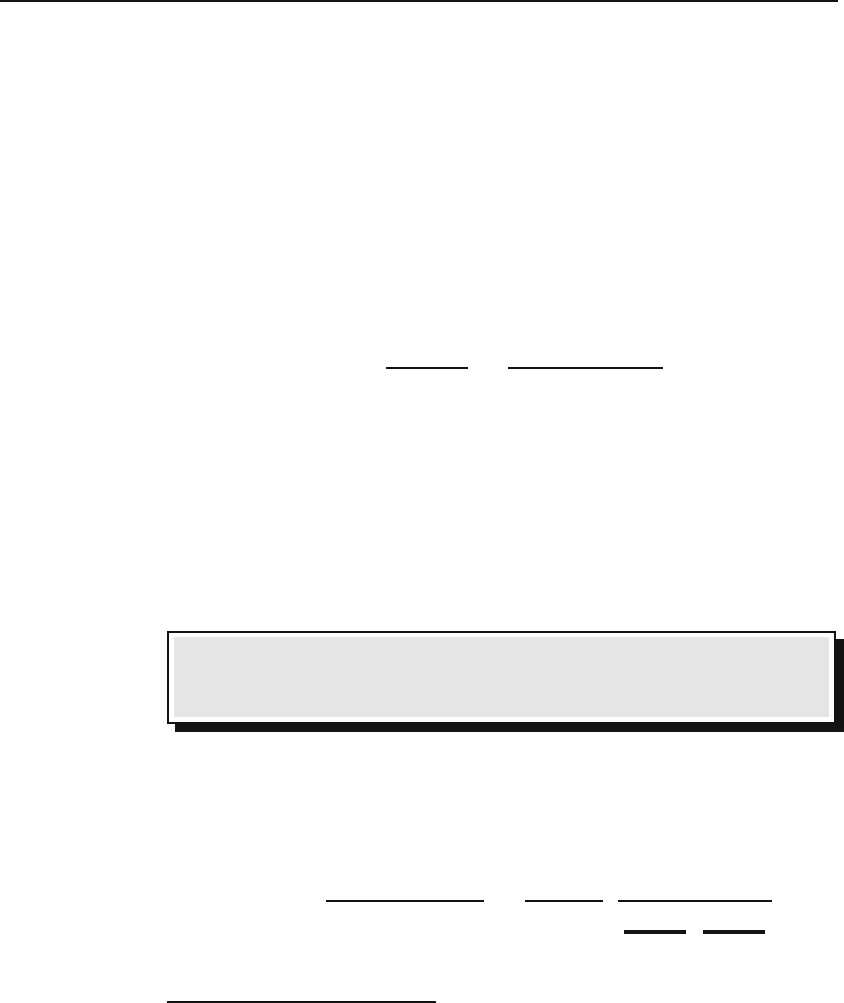
x(1 −x)y



+[γ − (α + β +1)x]y



− αβy =0, (11.22)

where α, β,andγ are constants.

The series solution of this DE, called

the hypergeometric function can be written in terms of the gamma func-

hypergeometric

function

tion as

F (α, β; γ; x) ≡

Γ(γ)

Γ(α)Γ(β)

∞



n=0

Γ(α + n)Γ(β + n)

Γ(γ + n)Γ(n +1)

. (11.23)

From this series representation, we immediately note that the hyperge-

ometric function is symmetric under interchange of α and β.Furthermore,

if either α or β is a negative integer,say−m, then the denominator of the

constant outside becomes inﬁnite by Deﬁnition 11.1.1. However, the gamma

function in the numerator of the ﬁrst m terms of the sum will also be inﬁnite.

The cancellation of these inﬁnities [see Problem 11.4(c)] gives a nonzero sum

up to m, but the rest of the series will be zero. Therefore,

Box 11.2.1. The hypergeometric function is symmetric under interchange

of α and β: F (α, β; γ; x)=F(β,α; γ; x).Furthermore,F (−m, β; γ; x)

[and therefore F (α, −m; γ; x)] is a polynomial if m is a positive integer.

As mentioned before, many a time, the inﬁnite series can be “integrated”

and the resulting function written in terms of an integral. In this case, we

start by multiplying and dividing the series of Equation (11.23) by Γ(γ − β)

to obtain

F (α, β; γ; x)=

Γ(γ)

Γ(α)Γ(β)Γ(γ − β)

∞



n=0

Γ(α + n)

Γ(n +1)

Γ(γ − β)Γ(β + n)

Γ(γ + n)



 

≡B(γ− β,β+n) by (11.7)

For a comprehensive treatment of this diﬀerential equation, see Hassani, S. Mathemati-

cal Physics: A Modern Introduction to Its Foundations, Springer-Verlag, 1999, Chapter 14.

Some authors use a, b,andc instead of α, β,andγ.

Some authors use

instead of F . Our use of F to represent both the elliptic integral

of the ﬁrst kind and the hypergeometric function should not cause any confusion because

the two functions have diﬀerent numbers of arguments (independent variables).

11.2 Power Series as Functions 329

Now use Γ(n +1)= n! and the integral representation of the beta function to

get

F (α, β; γ; x)=

Γ(γ)

Γ(α)Γ(β)Γ(γ−β)

∞



n=0

dt(1−t)

γ−β−1

β+n−1

Γ(α+n)

Γ(γ)

Γ(β)Γ(γ − β)

dt(1 −t)

γ−β−1

β−1

∞



n=0

Γ(α + n)

Γ(α)

(tx)

Using the result of Problem 11.4, we can now write

integral

representation of

the

hypergeometric

function

F (α, β; γ; x)=

Γ(γ)

Γ(β)Γ(γ − β)

dt(1 −t)

γ−β−1

β−1

(1 −tx)

−α

. (11.24)

This is the integral representation of the hypergeometric function.

The generality of the hypergeometric DE results in the ability to express

many functions—both elementary and the so-called special functions of math-

ematical physics—in terms of the hypergeometric function. For example, con-

sider the complete elliptic integral of the second kind E(k). The two factors of

double factorials in both the numerator and denominator of its series expan-

sion (see Problem 11.13), together with Equation (11.5) and the hypergeomet-

ric series (11.23), hint at the possibility of writing E(k)asahypergeometric

function. This is indeed the case. Substituting (11.5) in the expansion of

E(k) as given in Problem 11.13 yields

E(k)=

1 −

∞



n=1

Γ(n +

)Γ(n +

)π

−1

Γ(n +1)Γ(n +1)

2(n −

)

−

∞



n=1

Γ(n +

)Γ(n −

)

Γ(n +1)Γ(n +1)

)

where we used Γ(n +

)=(n −

)Γ(n −

). The sum starts with n =1. To

make it look like a hypergeometric series, we need to include the zero term as

well. Adding and subtracting this term gives

E(k)=

−

∞



n=0

Γ(n +

)Γ(n −

)

Γ(n +1)Γ(n +1)

)



Γ(

)Γ(−

)

Γ(1)Γ(1)

)



= −

∞



n=0

Γ(n +

)Γ(n −

)

Γ(n +1)Γ(n +1)

)

because Γ(−

)=−2Γ(

)=−2

√

π by Example 11.1.1. We now note that

except for a multiplicative constant, the sum is that of the hypergeometric

function with α =

= −β and γ = 1. Inserting the multiplicative constant

Γ(1)

Γ(

)Γ(−

)

(−2π)

330 Integrals and Series as Functions

we obtain

E(k)=

, −

;1;k

. (11.25)

The reader may verify that

K(k)=

;1;k

. (11.26)

Historical Notes

Johann Carl Friedrich Gauss was the greatest of all mathematicians and perhaps

the most richly gifted genius of whom there is any record. He was born in the city of

Brunswick in northern Germany. His exceptional skill with numbers was clear at a

very early age, and in later life he joked that he knew how to count before he could

talk. It is said that Goethe wrote and directed little plays for a puppet theater when

he was six and that Mozart composed his ﬁrst childish minuets when he was ﬁve,

but Gauss corrected an error in his father’s payroll accounts at the age of three. At

the age of seven, when he started elementary school, his teacher was amazed when

Gauss summed the integers from 1 to 100 instantly by spotting that the sum was

50 pairs of numbers each pair summing to 101.

His long professional life is so ﬁlled with accomplishments that it is impossible

to give a full account of them in the short space available here. All we can do is

simply give a chronology of his almost uncountable discoveries.

1792–1794: Gauss reads the works of Newton, Euler,andLagrange;discoversthe

prime number theorem (at the age of 14 or 15); invents the method of least squares;

conceives the Gaussian law of distribution in the theory of probability.

1795: (only 18 years old!) Proves that a regular polygon with n sidesisconstructible

(by ruler and compass) if and only if n is the product of a power of 2 and distinct

prime numbers of the form p

+ 1, and completely solves the 2000-year old

problem of ruler-and-compass construction of regular polygons. He also discovers

the law of quadratic reciprocity.

Carl Friedrich

Gauss 1777–1855

1799:Provesthefundamental theorem of algebra in his doctoral dissertation

using the then-mysterious complex numbers with complete conﬁdence.

1801: Gauss publishes his Disquisitiones Arithmeticae in which he creates the mod-

ern rigorous approach to mathematics; predicts the exact location of the asteroid

Ceres.

1807: Becomes professor of astronomy and the director of the new observatory at

G¨ottingen.

1809: Publishes his second book, Theoria motus corporum coelestium, a major

two-volume treatise on the motion of celestial bodies and the bible of planetary as-

tronomers for the next 100 years.

1812: Publishes Disquisitiones generales circa seriem inﬁnitam, a rigorous treat-

ment of inﬁnite series, and introduces the hypergeometric function for the ﬁrst

time, for which he uses the notation F(α, β; γ; z); an essay on approximate integra-

tion.

1820–1830: Publishes over 70 papers, including Disquisitiones generales circa su-

perﬁcies curvas, in which he creates the intrinsic diﬀerential geometry of general

curved surfaces, the forerunner of Riemannian geometry and the general theory of

relativity.

11.2 Power Series as Functions 331

From the 1830s on, Gauss was increasingly occupied with physics, and he en-

riched every branch of the subject he touched. In the theory of surface tension,

he developed the fundamental idea of conservation of energy and solved the earli-

est problem in the calculus of variations.Inoptics, he introduced the concept

of the focal length of a system of lenses. He virtually created the science of geo-

magnetism, and in collaboration with his friend and colleague Wilhelm Weber he

invented the electromagnetic telegraph. In 1839 Gauss published his fundamental

paper on the general theory of inverse square forces, which established potential

theory as a coherent branch of mathematics and in which he established the di-

vergence theorem.

Gauss had many opportunities to leave G¨ottingen, but he refused all oﬀers and

remained there for the rest of his life, living quietly and simply, traveling rarely, and

working with immense energy on a wide variety of problems in mathematics and

its applications. Apart from science and his family—he married twice and had six

children, two of whom emigrated to America—his main interests were history and

world literature, international politics, and public ﬁnance. He owned a large library

of about 6000 volumes in many languages, including Greek, Latin, English, French,

Russian, Danish, and of course German. His acuteness in handling his own ﬁnancial

aﬀairs is shown by the fact that although he started with virtually nothing, he left

an estate over a hundred times as great as his average annual income during the last

half of his life.

The foregoing list is the published portion of Gauss’s total achievement; the un-

published and private part is almost equally impressive. His scientiﬁc diary, a little

booklet of 19 pages, discovered in 1898, extends from 1796 to 1814 and consists of 146

very concise statements of the results of his investigations, which often occupied him

for weeks or months. These ideas were so abundant and so frequent that he physi-

cally did not have time to publish them. Some of the ideas recorded in this diary:

Cauchy Integral Formula: Gauss discovers it in 1811, 16 years before Cauchy.

Non-Euclidean Geometry: After failing to prove Euclid’s ﬁfth postulate at the

age of 15, Gauss came to the conclusion that the Euclidean form of geometry cannot

be the only one possible.

Elliptic Functions: Gauss had found many of the results of Abel and Jacobi (the

two main contributors to the subject) before these men were born. The facts became

known partly through Jacobi himself. His attention was caught by a cryptic passage

in the Disquisitiones, whose meaning can only be understood if one knows some-

thing about elliptic functions. He visited Gauss on several occasions to verify his

suspicions and tell him about his own most recent discoveries, and each time Gauss

pulled 30-year-old manuscripts out of his desk and showed Jacobi what Jacobi had

just shown him. After a week’s visit with Gauss in 1840, Jacobi wrote to his brother,

“Mathematics would be in a very diﬀerent position if practical astronomy had not

diverted this colossal genius from his glorious career.”

A possible explanation for not publishing such important ideas is suggested by

his comments in a letter to Bolyai: “It is not knowledge but the act of learning, not

possession but the act of getting there, which grants the greatest enjoyment. When

I have clariﬁed and exhausted a subject, then I turn away from it in order to go into

darkness again.” His was the temperament of an explorer who is reluctant to take the

time to write an account of his last expedition when he could be starting another. As

it was, Gauss wrote a great deal, but to have published every fundamental discovery

he made in a form satisfactory to himself would have required several long lifetimes.

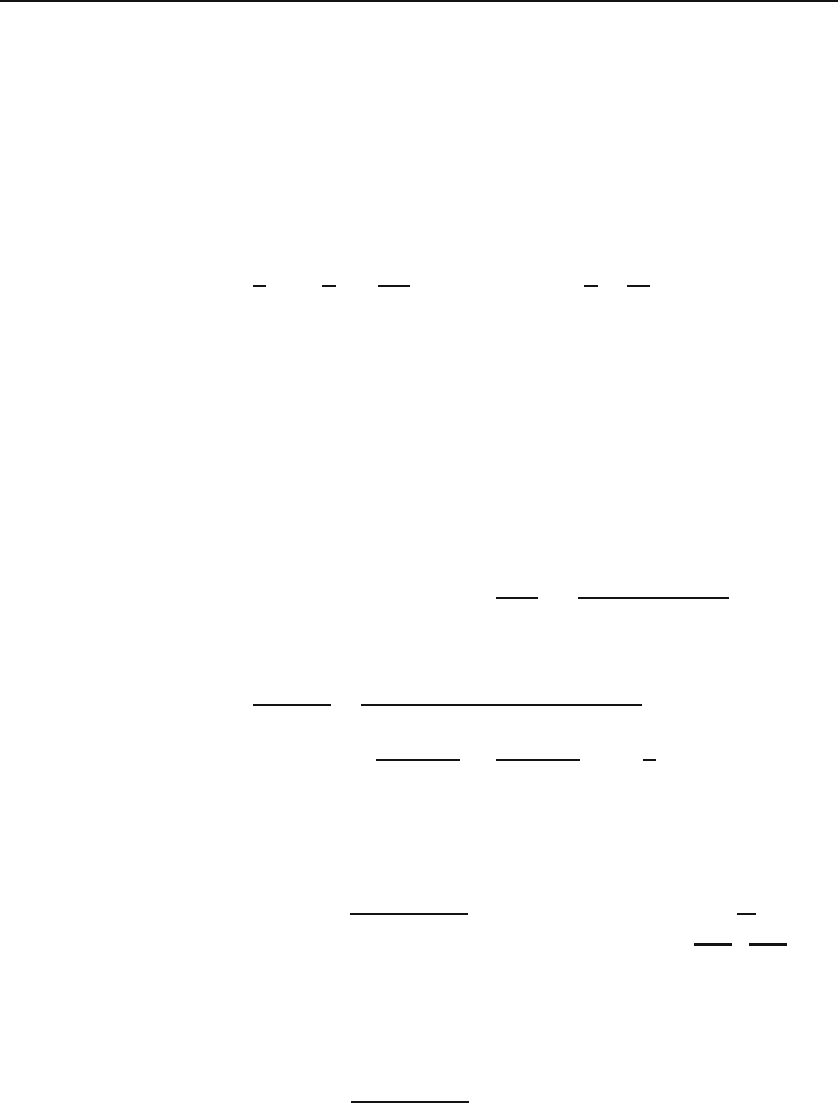
332 Integrals and Series as Functions

11.2.2 Conﬂuent Hypergeometric Functions

The parameters α, β,andγ determine the behavior of the hypergeometric

function completely. A great number of diﬀerential equations in mathematical

physics correspond to the case where only two parameters are involved. The

most eﬀective way of accommodating this arises from the conﬂuence β →∞.

Let us see how this works.

Substitute x = u/β in the hypergeometric DE using the—very simple—

chain rule to transform the x-derivatives to the u-derivatives. This leads to

the DE



1 −





γ − (α + β +1)



− αβy =0.

Dividing the entire equation by β, taking the limit β →∞—thus neglecting

u/β and 1/β—yields the so-called conﬂuent hypergeometric diﬀerential

equation:

conﬂuent

hypergeometric

diﬀerential

equation



+(γ −x)y



− αy =0, (11.27)

wherewerestoredx as the independent variable.

The inﬁnite series solution of this DE is called the conﬂuent hypergeo-

metric function. This solution, as well as its integral representation, can be

conﬂuent

hypergeometric

function

obtained by taking the appropriate limit of the corresponding expression for

the hypergeometric function. The limit of Equation (11.23) yields

Φ(α; γ; x) ≡ lim

β→∞

F (α, β; γ; x/β)=

Γ(γ)

Γ(α)

∞



n=0

Γ(α + n)

Γ(γ + n)Γ(n +1)

, (11.28)

whereweused

Γ(β + n)

Γ(β)

(β + n − 1)(β + n −2) ···βΓ(β)

Γ(β)



β + n −1



β + n −2



···





β→∞

−−−−→ 1.

Similarly, we have

Φ(α; γ; x) = lim

β→∞

F (β, α; γ; x/β)

= lim

β→∞

Γ(γ)

Γ(α)Γ(γ − α)

dt(1 −t)

γ−α−1

α−1



1 −



−β

  

→e

(Prob. 11.3)

where we have used the symmetry of the hypergeometric function under inter-

change of its ﬁrst two parameters. It follows that the integral representation

integral

representation of

the conﬂuent

hypergeometric

function

of the conﬂuent hypergeometric function is

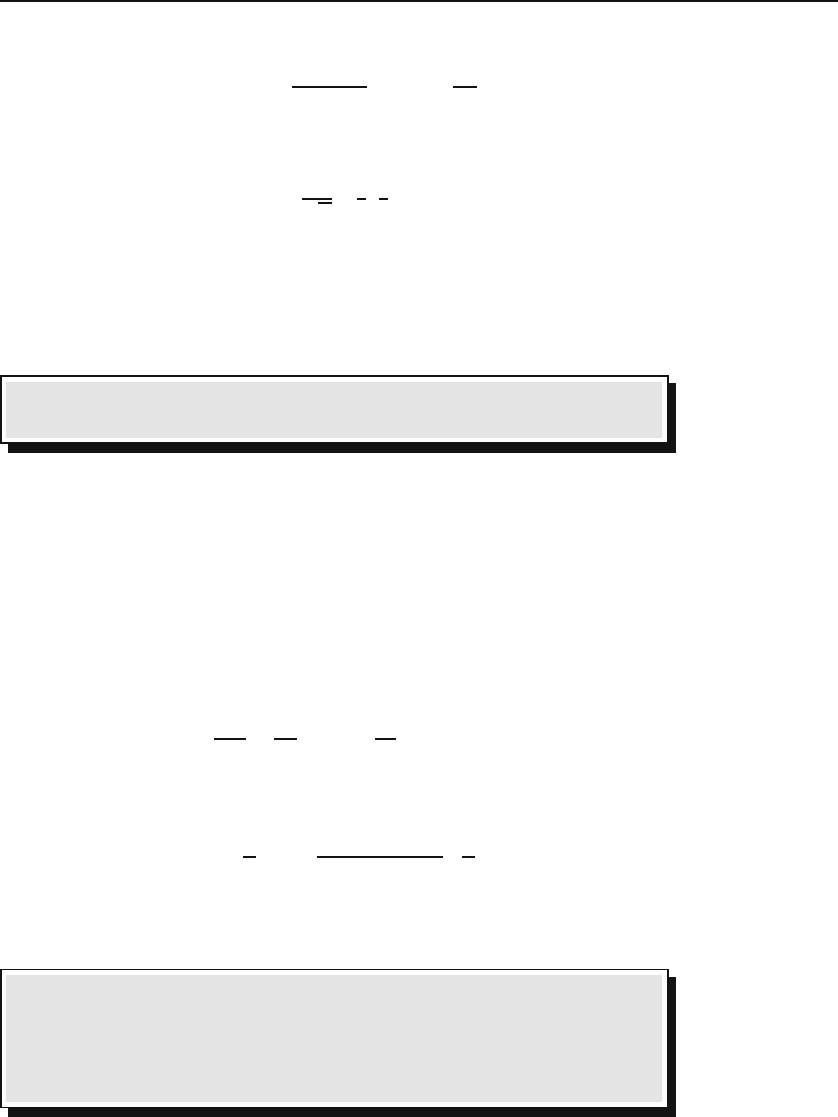
Φ(α; γ; x)=

Γ(γ)

Γ(α)Γ(γ − α)

dt(1 −t)

γ−α−1

α−1

. (11.29)

11.2 Power Series as Functions 333

We note that

Φ(α; α; x)=

∞



n=0

Γ(n +1)

∞



n=0

= e

and Problem 11.20 shows that

erf(x)=

√

Φ(

;

; −x

Many other functions encountered in mathematical physics can also be ex-

pressed in terms of conﬂuent hypergeometric functions, and we shall point

this out as we come across these functions in the sequel. We note in passing

that, as in the case of hypergeometric function,

Box 11.2.2. If α happens to be a negative integer, then Φ(α; γ; x) becomes

a polynomial, i.e., the inﬁnite series truncates.

11.2.3 Bessel Functions

Bessel functions are arguably among the most utilized functions of mathe-

matical physics. We shall come back to them when we consider solutions of

Laplace’s equation in cylindrical coordinates and discover their connection

with other functions treated in this chapter. At this point, we simply intro-

duce them as power series. The Bessel function J

(x)oforderν is a solution

of the Bessel diﬀerential equation:

Bessel diﬀerential

equation



x −



y =0. (11.30)

Chapter 27 shows how to obtain the power series expansion of J

(x):

(x)=





∞



k=0

(−1)

k!Γ(ν + k +1)





. (11.31)

The point to emphasize is that

Box 11.2.3. Bessel functions are always given in terms of their expan-

sion in power series (or as an integral involving parameters). It is gener-

ally impossible to reduce Bessel functions to any functional combination

of more elementary functions such as polynomials, or trigonometric and

exponential functions.

334 Integrals and Series as Functions

Properties and applications of Bessel functions are treated in some detail in

Chapter 27.

However, some relations are elementary enough to be included

here, as they also illustrate the use of summation symbols. First note that if

ν is an integer −m,then

−m

(x)=





−m

∞



k=0

(−1)

k!Γ(−m + k +1)









−m

∞



k=m

(−1)

k!Γ(−m + k +1)





because the ﬁrst m terms of the ﬁrst series have gamma functions in the

denominator with negative integer (or zero) arguments. Now in the second

series, replace k by n = k − m. This yields

−m

(x)=





−m

∞



n=0

(−1)

m+n

(m + n)!Γ(n +1)





2m+2n

(11.32)

=(−1)





∞



n=0

(−1)

Γ(m + n +1)n!





=(−1)

(x),

whereweusedΓ(j +1)=j! for positive integer j.

Example 11.2.1.

Bessel functions of half-integer order are related to trigonomet-

ric functions. To see this, note that

1/2





1/2

∞



k=0

(−1)

k!Γ(k +

)









−1/2

∞



k=0

(−1)

k!Γ(k +

2k+1

Now substitute for Γ(k +

) in terms of factorials as given in Problem 11.1 to obtain

1/2





−1/2

√

∞



k=0

(−1)

(2k +1)!

2k+1

  

=sin x



πx



1/2

sin x.

Similarly,

−1/2



πx



1/2

cos x

as the reader may verify.



See also Hassani, S. Mathematical Physics: A Modern Introduction to Its Foundations,

Springer-Verlag, 1999, Section 14.5.

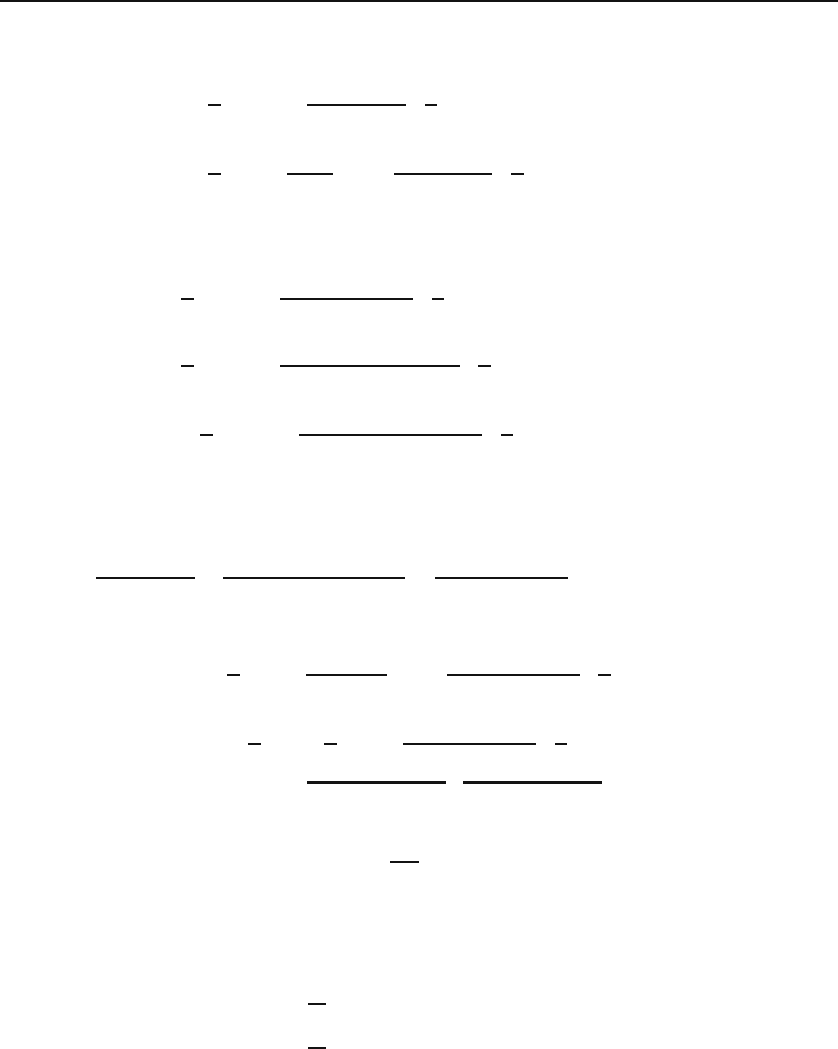
11.2 Power Series as Functions 335

Another formula of interest is a recursion relation connecting Bessel func-

tions of diﬀerent integer orders. Write J

m−1

(x)as

m−1

(x)=





m−1

∞



k=0

(−1)

k!Γ(m + k)





(11.33)





m−1

Γ(m)

∞



k=1

(−1)

k!Γ(m + k)





where we separated the k = 0 term from the rest of the sum. Similarly, write

m+1

(x)as

m+1

(x)=





m+1

∞



k=0

(−1)

k!Γ(m + k +2)









m+1

∞



j=1

(−1)

j−1

(j − 1)!Γ(m + j +1)





2j−2

(11.34)

= −





m−1

∞



k=1

(−1)

(k − 1)!Γ(m + k +1)





where in the second line, we substituted j = k +1 fork, and in the last line,

we used (−1)

−1

= −1, factored (x/2)

−2

out of the summation, and changed

the dummy index back to k. Now add Equations (11.33) and (11.34) and use

k!Γ(m + k)

−

(k − 1)!Γ(m + k +1)

k!Γ(m + k +1)

and 1/Γ(m)=m/Γ(m +1) toobtain

m−1

(x)+J

m+1

(x)=





m−1

Γ(m +1)

∞



k=1

(−1)

k!Γ(m + k +1)





= m





−1





∞



k=0

(−1)

k!Γ(m + k +1)







 

(x)

or, ﬁnally,

m−1

(x)+J

m+1

(x)=

(x). (11.35)

The straightforward details are left as Problem 11.22. One can also show that

m−1

(x) −J

m+1

(x)=2J



(x), (11.36)

where prime indicates diﬀerentiation. Equations (11.35) and (11.36) lead to

m−1

(x)=

(x)+J



(x),

m+1

(x)=

(x) −J



(x). (11.37)

These plus the results of Example 11.2.1 give all Bessel functions of half-

integer order.

336 Integrals and Series as Functions

11.3 Problems

11.1. (a) Show that (see Deﬁnition 11.1.2 for the deﬁnition of the following

notation):

(2n)!! = 2

n!and(2n − 1)!! =

(2n)!

Hint: For the second relation, supply the missing even factors in the “numer-

ator” and the “denominator” of (2n − 1)!!

(b) Using (a) and Example 11.1.1, show that

Γ(n +

(2n −1)!!

√

π =

(2n)!

√

π.

Γ(n +

(2n +1)!

2n+1

√

π.

11.2. Using the result of Problem 11.1, show that

(2n + m)! =

√

2n+m



n +





n +

m +1



Hint: Consider the two cases of even m (with m =2k)andoddm (with

m =2k + 1) separately, and show at the end that both can be written as a

single formula.

11.3. Using the result

lim

n→∞





= e

show that

lim

n→∞



1 −



= e

−t

Hint: Let n = −tm.

11.4. (a) By using Equation (11.2) repeatedly, show that

Γ(a + n)=(a + n − 1)(a + n − 2) ···(a + n − k)Γ(a + n −k).

(b) Let k = n in the above equation to show that

a(a +1)···(a + n −1) =

Γ(a + n)

Γ(a)

α(α −1) ···(α −n +1)=(−1)

Γ(n −α)

Γ(−α)