Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

12.1 Solid Angle 349
of solid angles. In particular, if the surface S is closed and P is inside, then
A will be the total area of the fiducial sphere and we get Ω = 4πb
2
/b
2
=4π.
When P is outside, we get equal amounts of positive and negative contribu-
tions with the net result of zero.
total solid angle at
a point subtended
by a closed surface
Theorem 12.1.2. Denote by Ω
S
P
the total solid angle subtended by the closed
surface S about a point P and by V the region enclosed by S.Then,
Ω
S
P
=
0
4π if P is in V,
0 if P is not in V.
(12.7)
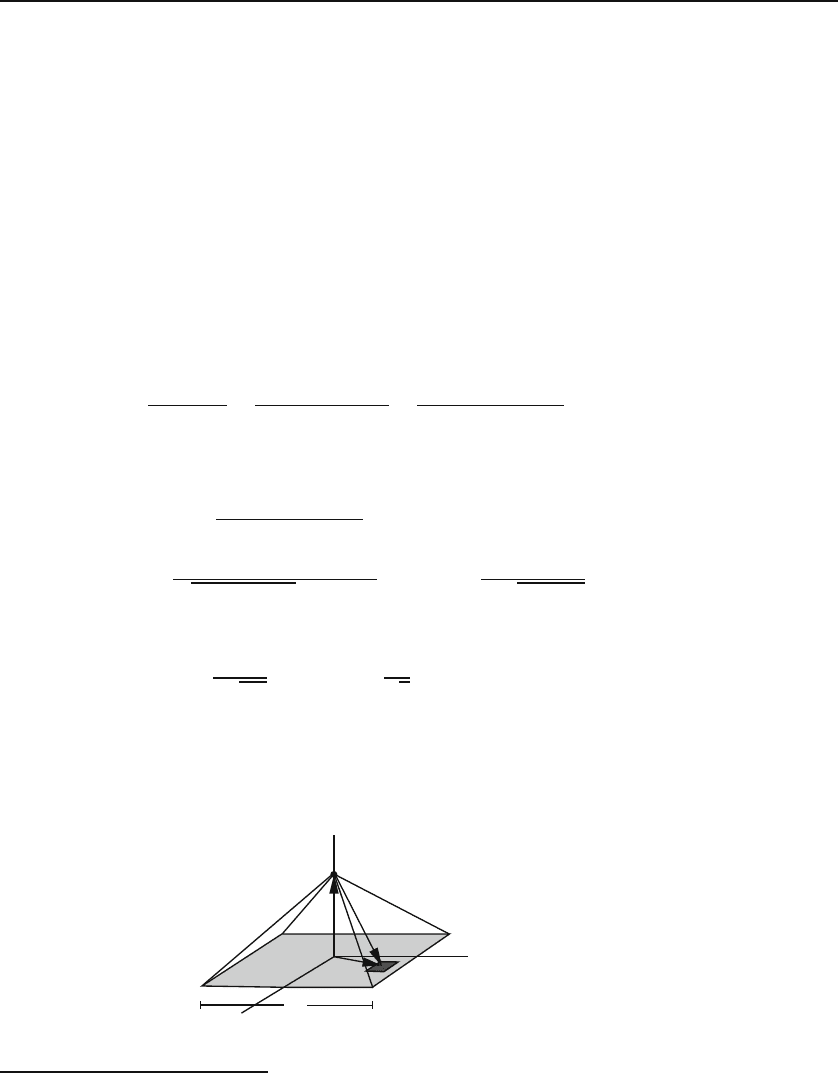
Example 12.1.3.
As an example of the calculation of the solid angle, consider a
square of side 2a with the point P located a distance z
0
from its center as shown in
Figure 12.6. With r = 0, 0,z
0
and r
= x
,y
, 0,wehaveR = r
−r = x
,y
, −z
0
,
and assuming that
ˆ
e
n
points in the negative z-direction,
4
we have
dΩ=
da
ˆ
e
n
·
ˆ
e
R
R
2
=
dx
dy
(−
ˆ
e
z
) · R
R
3
=
z
0
dx
dy
(x
2
+ y
2
+ z
2
0
)
3/2
.
The solid angle is obtained by integrating this:
Ω=z
0
#
a
−a
dx
#
a
−a
dy
(x
2
+ y
2
+ z
2
0
)
3/2
=2az
0
#
a
−a
dx
x
2
+ a
2
+ z
2
0
(x
2
+ z
2
0
)
=4tan
−1
a
2
z
0
2a
2
+ z
2
0
.
An interesting special case is when z
0
= a.Then
Ω=4tan
−1
a
2
a
√
3a
2
=4tan
−1
1
√
3
=4(π/6) = 2π/3.
The last result can also be derived in a simpler way. When z
0
= a,thepointP will
be at the center of a cube of side 2a. Since the total solid angle subtended about P
is 4π, and all six sides contribute equally, the solid angle subtended by one side is
4π/6.
r
P
2a
r
'
Figure 12.6: The solid angle subtended by a square of side 2a.
4
This assumption is not forced by any convention. It is chosen to make the final result
positive.
350 Vectors and Derivatives
Example 12.1.4. Let us replace the square of the last example with a circle of
radius a. We can proceed along the same lines as before. However, in this particular
case, we note that the solid angle is in the shape of a cone which is one of the
primary surfaces of the spherical coordinate system. Placing the origin at P and
projecting the area on a fiducial sphere, of radius b say, we may write
Ω=
A
b
b
2
=
2πb
2
(1 − cos α)
b
2
=2π(1 − cos α),
where A
b
≡ 2πb
2
(1 −cos α) is the area of the projection of the circle on the fiducial
sphere. The half-angle of the cone is denoted by α with
tan α =
a
z
0
⇒ cos α =
z
0
a
2
+ z
2
0
.
The final result is
Ω=2π
1 −
z
0
a
2
+ z
2
0
. (12.8)
It is instructive to obtain this result directly as in the previous example.
12.2 Time Derivative of Vectors
Scalar and vector fields can be subjected to such analytic operations as differ-
entiation and integration to obtain new scalar and vector fields. The deriva-
tive of a vector with respect to a variable (say time) in Cartesian coordinates
amounts to differentiating each component:
∂A
∂t
=
∂A
x
∂t
ˆ
e
x
+
∂A
y
∂t
ˆ
e
y
+
∂A
z
∂t
ˆ
e
z
. (12.9)
In other coordinate systems, one needs to differentiate the unit vectors as well.
In general, the derivative of a vector is defined in exactly the same manner
as for ordinary functions. We have to keep in mind that a vector physical
quantity, such as an electric field, is a function of space and time, i.e., its
components are real-valued functions of space and time. So, consider a vector
A which is a function of a number of independent variables (t
1
,t
2
,...,t
m
).
Then, we define the partial derivative as before:
∂A
∂t
k
(a
1
,a
2
,...,a
n
)
≡ lim
→0
A(a
1
,...,a
k
+ ,...,a
n
) −A(a
1
,...,a
k
,...,a
n
)
.
(12.10)
As immediate consequences of this definition, we list the following useful
relations:
∂
∂t
k
(fA)=
∂f
∂t
k
A + f
∂A
∂t
k
,
∂
∂t
k
(A · B)=
∂A
∂t
k
·B + A ·
∂B
∂t
k
, (12.11)
∂
∂t
k
(A × B)=
∂A
∂t
k
× B + A ×
∂B
∂t
k
.
12.2 Time Derivative of Vectors 351
These relations can be used to calculate the derivatives of vectors when written
in terms of unit vectors, keeping in mind that the derivative of a unit vector
is not necessarily zero! Only Cartesian unit vectors are constant vectors, and
only Cartesian
unit vectors are
constant.
for purposes of differentiation, it is convenient to write vectors in terms of
these unit vectors, perform the derivative operation, and then substitute for
ˆ
e
x
,
ˆ
e
y
,and
ˆ
e
z
in terms of other—spherical or cylindrical—unit vectors.
Example 12.2.1.
A vector whose magnitude is constant is always perpendicular
to its derivative. This can be easily proved as follows:
A · A =const. ⇒
∂
∂t
k
(A · A)=
∂
∂t
k
(const.) = 0.
On the other hand, the LHS can be evaluated using the second relation in Equation
(12.11). This gives
∂
∂t
k
(A · A)=
∂A
∂t
k
· A + A ·
∂A
∂t
k
=2A ·
∂A
∂t
k
.
These two equations together imply that A and (∂/∂t
k
)(A) are perpendicular to
one another.
An important consequence of the example above is that
Box 12.2.1. A unit vector is always perpendicular to its derivative.
Example 12.2.2. Newton’s second law for a collection of particles leads directly
to the corresponding law for rotational motion. Differentiating the total angular
momentum
L =
N
k=1
r
k
× p
k
,
with respect to time and using the second law, F
k
= dp
k
/dt,forthekth particle,
we get
dL
dt
=
N
k=1
d
dt
(r
k
× p
k
)=
N
k=1
(
˙
r
k
× p
k
+ r
k
×
˙
p
k
)=
N
k=1
(0 + r
k
× F
k
) ≡ T,
where an overdot indicates the derivative with respect to time and in the last line
we used the definition of torque and the fact that velocity
˙
r
k
and momentum p
k
have the same direction.
As a special case of the example above, we obtain the law of angular
momentum conservation:
angular
momentum
conservation
Box 12.2.2. When the total torque on a system of particles vanishes, the
total angular momentum will be a constant of motion. This means that
its components in a Cartesian coordinate system are constant.
Since the unit vectors in other coordinate systems are not, in general, constant,
a constant vector has variable components in these systems.

352 Vectors and Derivatives
12.2.1 Equations of Motion in a Central Force Field
When one discusses the central-force problems in mechanics, for instance in
the study of planetary motion, one uses spherical coordinates to locate the
moving object. Thus, the position vector of the object, say a planet, is given
in terms of spherical unit vectors. Newton’s second law, on the other hand,
requires a knowledge of the second time-derivative of the position vector.
In this subsection we find the second derivative of the position vector of
a moving point particle P with respect to time in spherical coordinates. The
coordinates (r, θ, ϕ)ofP are clearly functions of time. First we calculate
velocity and write it in terms of the spherical unit vectors
v =
dr
dt
=
d
dt
(r)=
d
dt
(r
ˆ
e
r
)=
ˆ
e
r
dr
dt
+ r
d
ˆ
e
r
dt
.
We thus have to find the time-derivative of the unit vector
ˆ
e
r
.Themost
straightforward way of taking such a derivative is to use the chain rule:
d
ˆ
e
r
dt
=
∂
ˆ
e
r
∂r
dr
dt
+
∂
ˆ
e
r
∂θ
dθ
dt
+
∂
ˆ
e
r
∂ϕ
dϕ
dt
=
˙
θ
∂
ˆ
e
r
∂θ
+˙ϕ
∂
ˆ
e
r
∂ϕ
,
where we have used the fact that the spherical unit vectors are independent
of r [see Equation (1.39)]. We now evaluate the partial derivatives using (1.39)
and noting that the Cartesian unit vectors are constant:
∂
ˆ
e
r
∂θ
=
ˆ
e
x
∂
∂θ
(sin θ cos ϕ)+
ˆ
e
y
∂
∂θ
(sin θ sin ϕ)+
ˆ
e
z
∂
∂θ
(cos θ)
=
ˆ
e
x
cos θ cos ϕ +
ˆ
e
y
cos θ sin ϕ −
ˆ
e
z
sin θ. (12.12)
We are interested in writing all vectors in terms of spherical coordinates. A
straightforward way is to substitute for the above Cartesian unit vectors, their
expressions in terms of spherical unit vectors. We can easily calculate such
expressions using the method introduced at the end of Chapter 1. We leave
the details for the reader and merely state the results:
ˆ
e
x
=
ˆ
e
r
sin θ cos ϕ +
ˆ
e
θ
cos θ cos ϕ −
ˆ
e
ϕ
sin ϕ,
ˆ
e
y
=
ˆ
e
r
sin θ sin ϕ +
ˆ
e
θ
cos θ sin ϕ +
ˆ
e
ϕ
cos ϕ, (12.13)
ˆ
e
z
=
ˆ
e
r
cos θ −
ˆ
e
θ
sin θ.
Substituting these expressions in the previous equation, we get
∂
ˆ
e
r
∂θ
=(
ˆ
e
r
sin θ cos ϕ +
ˆ
e
θ
cos θ cos ϕ −
ˆ
e
ϕ
sin ϕ)cosθ cos ϕ
+(
ˆ
e
r
sin θ sin ϕ +
ˆ
e
θ
cos θ sin ϕ +
ˆ
e
ϕ
cos ϕ)cosθ sin ϕ
− (
ˆ
e
r
cos θ −
ˆ
e
θ
sin θ)sinθ,
which simplifies to
∂
ˆ
e
r
∂θ
=
ˆ
e
θ
. (12.14)

12.2 Time Derivative of Vectors 353
We could have immediately obtained this result by comparing Equation (12.12)
with the expression for
ˆ
e
θ
in Equation (1.39). The other partial derivative is
obtained the same way:
∂
ˆ
e
r
∂ϕ
=
ˆ
e
x
∂
∂ϕ
(sin θ cos ϕ)+
ˆ
e
y
∂
∂ϕ
(sin θ sin ϕ)+
ˆ
e
z
∂
∂ϕ
(cos θ)
= −
ˆ
e
x
sin θ sin ϕ +
ˆ
e
y
sin θ cos ϕ
= −(
ˆ
e
r
sin θ cos ϕ +
ˆ
e
θ
cos θ cos ϕ −
ˆ
e
ϕ
sin ϕ)sinθ sin ϕ
+(
ˆ
e
r
sin θ sin ϕ +
ˆ
e
θ
cos θ sin ϕ +
ˆ
e
ϕ
cos ϕ)sinθ cos ϕ
=
ˆ
e
ϕ
sin θ. (12.15)
Substituting this and Equation (12.14) in the expression for velocity, we obtain
components of
velocity in
spherical
coordinates
v =
ˆ
e
r
˙r + r
˙
θ
∂
ˆ
e
r
∂θ
+˙ϕ
∂
ˆ
e
r
∂ϕ
=
ˆ
e
r
˙r +
ˆ
e
θ
r
˙
θ +
ˆ
e
ϕ
r ˙ϕ sin θ. (12.16)
To write the equations of motion, we need to calculate the acceleration
which involves the differentiation of other unit vectors. The procedure out-
lined for
ˆ
e
r
can be used to obtain the partial derivatives of the other unit vec-
tors. We collect the result of such calculations, including Equations (12.14)
and (12.15) in the following:
∂
ˆ
e
r
∂r
=0,
∂
ˆ
e
r
∂θ
=
ˆ
e
θ
,
∂
ˆ
e
r
∂ϕ
=
ˆ
e
ϕ
sin θ,
∂
ˆ
e
θ
∂r
=0,
∂
ˆ
e
θ
∂θ
= −
ˆ
e
r
,
∂
ˆ
e
θ
∂ϕ
=
ˆ
e
ϕ
cos θ, (12.17)
∂
ˆ
e
ϕ
∂r
=0,
∂
ˆ
e
ϕ
∂θ
=0,
∂
ˆ
e
ϕ
∂ϕ
= −
ˆ
e
r
sin θ −
ˆ
e
θ
cos θ.
Similarly the time-derivatives of the unit vectors are given as follows:
d
ˆ
e
r
dt
=
˙
θ
ˆ
e
θ
+˙ϕ sin θ
ˆ
e
ϕ
,
d
ˆ
e
θ
dt
= −
˙
θ
ˆ
e
r
+˙ϕ cos θ
ˆ
e
ϕ
, (12.18)
d
ˆ
e
ϕ
dt
= − ˙ϕ sin θ
ˆ
e
r
− ˙ϕ cos θ
ˆ
e
θ
.
Differentiating Equation (12.16) with respect to t, inserting (12.18) in the
result, and collecting the components, we get
components of
acceleration in
spherical
coordinates
d
2
r
dt
2
=
dv
dt
=
ˆ
e
r
¨r − r
˙
θ
2
− r ˙ϕ
2
sin
2
θ
+
ˆ
e
θ
˙r
˙
θ +
d
dt
(r
˙
θ) − r ˙ϕ
2
sin θ cos θ
(12.19)
+
ˆ
e
ϕ
˙r ˙ϕ sin θ + r
˙
θ ˙ϕ cos θ +
d
dt
(r ˙ϕ sin θ)
.

354 Vectors and Derivatives
One can use these expressions to write Newton’s second law in spherical
coordinates.
Now suppose that a particle (a planet) is under the influence of a central
force, i.e., a force that always points toward, or away from, an origin (the
Sun), and has a magnitude that is a function of the distance between the
particle and the origin. This means that, in spherical coordinates, the force
is of the form F =
ˆ
e
r
F (r). The second law of motion now yields
m
d
2
r
dt
2
=
ˆ
e
r
F (r) ⇒
d
2
r
dt
2
=
ˆ
e
r
F (r)
m
≡
ˆ
e
r
f(r)
which, together with Equation (12.19), gives
central-force
problem in
spherical
coordinates
¨r − r
˙
θ
2
− r ˙ϕ
2
sin
2
θ = f(r),
˙r
˙
θ +
d
dt
(r
˙
θ) −r ˙ϕ
2
sin θ cos θ =0, (12.20)
˙r ˙ϕ sin θ + r
˙
θ ˙ϕ cos θ +
d
dt
(r ˙ϕ sin θ)=0.
These equations are the starting point of the study of planetary motion.
We shall not pursue their solution at this point, but consider some of their
general properties, using angular momentum conservation. Since the force
has only an
ˆ
e
r
component, its torque vanishes:angular
momentum is
conserved in
motions caused by
central forces.
T = r × F = r
ˆ
e
r
× (F (r)
ˆ
e
r
)=rF (r)
ˆ
e
r
×
ˆ
e
r
=0.
Therefore, by Box 12.2.2, the angular momentum of the particle relative to
the origin is a constant vector. Equation (12.16) now yields
L = r × (mv)=mr
ˆ
e
r
×
ˆ
e
r
˙r +
ˆ
e
θ
r
˙
θ +
ˆ
e
ϕ
r ˙ϕ sin θ
= mr
2
ˆ
e
r
× (
ˆ
e
θ
˙
θ +
ˆ
e
ϕ
˙ϕ sin θ)=mr
2
(
ˆ
e
ϕ
˙
θ −
ˆ
e
θ
˙ϕ sin θ)
= mr
2
˙
θ(−
ˆ
e
x
sin ϕ +
ˆ
e
y
cos ϕ)
− mr
2
˙ϕ sin θ(
ˆ
e
x
cos θ cos ϕ +
ˆ
e
y
cos θ sin ϕ −
ˆ
e
z
sin θ)
= L
x
ˆ
e
x
+ L
y
ˆ
e
y
+ L
z
ˆ
e
z
,
where L
x
, L
y
,andL
z
are the constant Cartesian components of angular
momentum and m is the mass of the particle. Equating the components of
this vectorial relation gives
L
x
= −mr
2
(
˙
θ sin ϕ +˙ϕ sin θ cos θ cos ϕ),
L
y
= mr
2
(
˙
θ cos ϕ − ˙ϕ sin θ cos θ sin ϕ), (12.21)
L
z
= mr
2
˙ϕ sin
2
θ.
The last equation gives
˙ϕ =
L
z
mr
2
sin
2
θ
. (12.22)

12.3 The Gradient 355
From all of these relations, we obtain
L
2
= L
2
x
+ L
2
y
+ L
2
z
= m
2
r
4
˙
θ
2
+
L
2
z
sin
2
θ
. (12.23)
Now suppose that we choose our coordinate axes so that initially, i.e., at
t = 0, both the position and the velocity vectors of the particle lie in the xy-
plane. Since L is perpendicular to both r and v, it must be initially entirely
in the z-direction. Conservation of angular momentum implies that L will
always be in the z-direction. In particular, L
2
= L
2
z
. Substituting this in
Equation (12.23) yields
L
2
= m
2
r
4
˙
θ
2
+
L
2
sin
2
θ
⇒ 0=m
2
r
4
˙
θ
2
+
L
2
sin
2
θ
− L
2
or 0 = m
2
r
4
˙
θ
2
+ L
2
cot
2
θ. Neither of the two terms on the RHS of this
equation is negative. Thus, for their sum to be zero, each term must be zero.
It follows that
m
2
r
4
˙
θ
2
=0 ⇒
˙
θ =0 ⇒ θ =const.,
L
2
cot
2
θ =0 ⇒ cot
2
θ =0 ⇒ θ = π/2,
assuming that r =0andL = 0. These relations hold for all times.Thus,
proof that planets
move in a plane
the particle is confined to a plane, our xy-plane, for eternity! This is why the
planets do not wobble “up and down” out of their orbital planes.
5
If we substitute π/2forθ and use (12.22) for ˙ϕ in Equation (12.20), then
the second and third relations are satisfied identically, and the first relation
becomes
¨r −
L
2
m
2
r
3
= f (r) (12.24)
which is a single differential equation in one variable. The general problem
of a particle’s motion in three dimensions has reduced to a one-dimensional
problem.
12.3 The Gradient
Analysis of vectors deals with the derivatives and integrals of vector fields.
Because of its simplicity, we shall work in a Cartesian coordinate system at
the beginning, and later generalize to other coordinates.
In many situations arising in physics, rates of change of certain scalar
functions with distance are of importance. For instance, the way potential
energy changes as we move in space is directly related to the force producing
the potential energy. Similarly, the rate of change—derivative—of the elec-
trostatic potential with respect to distance gives the electrostatic field. The
concept of gradient makes precise the vague notion of a derivative with respect
to distance.
5
Actually, the planets, due to the influence of other planets, do wobble out of their
orbits. But this is a very small effect.

356 Vectors and Derivatives
y
x
f (x) Δx
Δ f
x
0
x
0
+
Δx
Figure 12.7: “Gradient” or differentiation with respect to distance in one dimension.
Let us analyze the notion of differentiation with respect to distance, start-
ing with one variable. In Figure 12.7, a function f(x) has an increment, Δf,
notion of ordinary
derivative
reexamined
corresponding to a change Δx in x.IfΔx is small enough, we can write
Δf ≈
df
dx
x=x
0
Δx.
This shows that (df / d x )
x=x
0
is a measure of how fast the function f is chang-
ing at the point x
0
.
With one variable, there is no ambiguity in defining the derivative, because
there is only one line along which we can change x, the only coordinate. With
two or more variables, the situation is completely different, as illustrated
in Figure 12.8. A point P
0
=(x
0
,y
0
)inthexy-plane is shown with the
corresponding value of the function, f (x
0
,y
0
)=z
0
. Out of the infinitude ofnotion of gradient
analyzed
points that are close to P
0
and cause a change in the function, only three are
shown. These indicate how the change in f (x, y) depends on the direction
in which the neighboring point is located in relation to P
0
. For example, if
we move in the direction P
0
P
1
, there is very little change in f(x, y), but if
we move in the direction P
0
P
2
, we notice more change in the function, and
if we move in the direction of P
0
P
3
, the change seems to be maximum. This
maximum change, and the direction associated with it, is called the gradient.
O
x
y
z
P
0
P
1
P
2
P
3
z
0
z
1
z
2
z
3
Figure 12.8: Gradient or differentiation with respect to distance is shown in two di-
mensions. The gradient is a vector in the xy-plane.Donotthinkofthesurfaceasa
variation in height! It could represent, for instance, the temperature at various points
of the xy-plane.
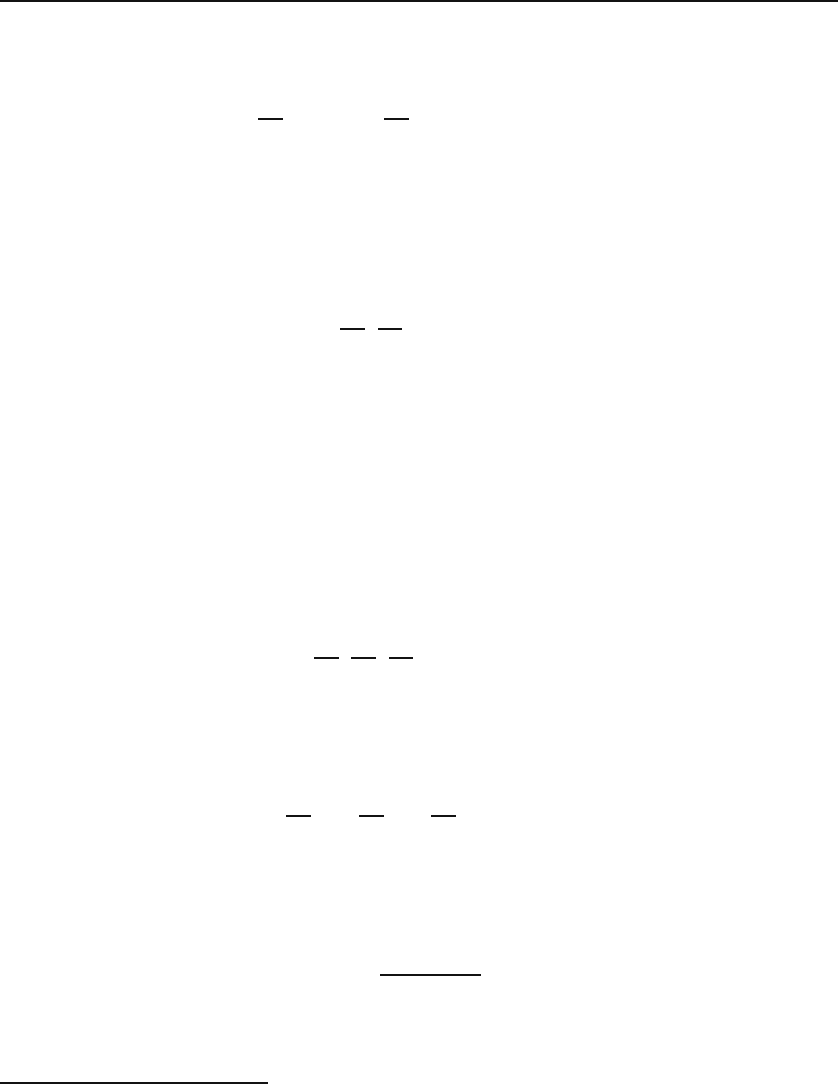
12.3 The Gradient 357
Let us use dr to denote the infinitesimal displacement vector
6
connecting
P
0
to a neighboring point in the xy-plane.Iff(x, y) is differentiable, Equation
(2.12) gives
df =
∂f
∂x
P
0
dx +
∂f
∂y
P
0
dy,
where dx and dy are the components of the displacement from P
0
and df is
(approximately) the change in f corresponding to the increments dx and dy.
We can rewrite this equation as
df =(∇f)
P
0
· dr = |∇f||dr|cos θ, (12.25)
where, by definition,
gradient in two
dimensions
(∇f)
P
0
≡
∂f
∂x
,
∂f
∂y
P
0
(12.26)
is a vector in the xy-plane and θ is the angle between this vector and dr.It
is clear that df will be maximum when cos θ =1,thatis,whendr is in the
direction of ∇f. We conclude, therefore, that ∇f gives the direction along
which f changes most rapidly. The vector in Equation (12.26) is the gradient
of f at P
0
.
The notion of gradient can be generalized to three variables although it is
harder to visualize than the two-variable case. In three dimensions we deal
with a function f(x, y, z)—which cannot be plotted as in Figure 12.8—and
ask which dr = dx, dy, dz maximizes the change in f. Once again, the
three-dimensional version of Equation (12.25) shows that dr and
gradient in three
dimensions
∇f ≡
∂f
∂x
,
∂f
∂y
,
∂f
∂z
(12.27)
should be in the same direction for df to have a maximum.
Definition 12.3.1. The gradient of a function f (x, y, z) is defined as
∇f ≡
ˆ
e
x
∂f
∂x
+
ˆ
e
y
∂f
∂y
+
ˆ
e
z
∂f
∂z
.
For the same small displacement |Δr|, the change in f is maximum when Δr
is in the direction of ∇f.
Example 12.3.1.
As an example, let us find the gradient of the function
V (x, y, z)=f(r)=f
x
2
+ y
2
+ z
2
(which depends on r alone) at a point P with Cartesian coordinates (x, y, z). Using
the chain rule, we have
6
A better notation is Δr. However, since there is no difference between differential
and increment of an independent variable, and since eventually we will be interested in
differentials, we use the latter notation.

358 Vectors and Derivatives
∇V =
ˆ
e
x
∂V
∂x
+
ˆ
e
y
∂V
∂y
+
ˆ
e
z
∂V
∂z
=
∂V
∂x
,
∂V
∂y
,
∂V
∂z
=
f
(r)
∂r
∂x
,f
(r)
∂r
∂y
,f
(r)
∂r
∂z
= f
(r)
C
x
r
,
y
r
,
z
r
D
=
f
(r)
r
x, y, z = f
(r)
r
r
.
The last equality shows that, for functions that depend on r alone, the gradient is
proportional to the position vector of the point P , i.e., it is radial.
Given a scalar function f (x, y, z), we can consider surfaces on which this
function maintains a constant value. If that constant value is C,thesurface
will be described by f (x, y, z)=C. One can, in principle, solve for z as a
function of x and y to find the explicit dependence of the function. However,
we are interested in the implicit dependence given above. Now consider two
points P
1
and P
2
on the surface with coordinates (x, y, z)and(x +Δx, y +
Δy, z +Δz), respectively. We have
f(x, y, z)=f (x +Δx, y +Δy, z +Δz) ⇒ f(x, y, z)=f(x, y, z)+Δf
or 0 = Δf ≈
∂f
∂x
Δx +
∂f
∂y
Δy +
∂f
∂z
Δz, if the increments of coordinates are
small. This relation shows that ∇f is perpendicular to the displacement
from P
1
to P
2
. The same argument applies to a curve g(x, y)=C; i.e., the
two-dimensional gradient is perpendicular to the displacement from P
1
to P
2
,
both being points on the curve. Since P
1
and P
2
are completely arbitrary, we
conclude that
Theorem 12.3.2. The gradient ∇f is perpendicular to all surfaces f(x, y, z)=
C for different C’s. Similarly, ∇g is perpendicular to all curves g(x, y)=C.
For example, as we shall see later, the electrostatic field is the gradient of
electrostatic field
is perpendicular to
surfaces of
conductors
the electrostatic potential. Therefore, the electrostatic field is perpendicular
to surfaces of constant potential such as conductors.
Example 12.3.3.
The perpendicularity property of the gradient can be used to
find the equation of the tangent plane to a surface z = g(x, y)atapointP with
coordinates (x
0
,y
0
,z
0
). This surface can be written as
f(x, y, z) ≡ z −g(x, y)=0.
Then, the normal to the surface at P —which is the same as the normal to the
tangent plane at P—is the gradient of f at P :
∇f
!
P
=
∂f
∂x
,
∂f
∂y
,
∂f
∂z
P
=
−
∂g
∂x
, −
∂g
∂y
, 1
P
.
A point of the tangent plane at P is completely determined by the property thatderivation of the
equation of a
plane tangent to a
surface
its displacement vector Δr from P should be perpendicular to the gradient at P (see
Figure 12.9). If we denote the position vector of P by r
0
and that of the point on
the plane by r = x, y, z, then the equation of the tangent plane is given by
(r − r
0
) · (∇f)
P
=0 ⇒−(x − x
0
)
∂g
∂x
P
− (y − y
0
)
∂g
∂y
P
+(z − z
0
)=0
