Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.

370 Flux and Divergence
by Maxwell’s time a great deal of vector analysis was created by treating the scalar
and vector parts of quaternions separately.
The formal break with quaternions and the inauguration of a new independent
subject, vector analysis, was made independently by Josiah Willard Gibbs and Oliver
Heaviside in the early 1880s.
13.1.1 Flux Through an Arbitrary Surface
It may be useful to have a general formula for calculating the flux through
an arbitrary surface whose equation is given in parametric form in Cartesian
coordinates. Let
x = f(u, v),y= g(u, v),z= h(u, v), (13.4)
be the parametric equation of a surface. When v is held fixed and u is allowed
to vary, a curve is traced on the surface whose infinitesimal displacement can
be written as [see Equation (6.63)]
d
l
1
=
ˆ
e
x
∂f
∂u
du +
ˆ
e
y
∂g
∂u
du +
ˆ
e
z
∂h
∂u
du.
Similarly infinitesimal displacement along curves of constant u is
d
l
2
=
ˆ
e
x
∂f
∂v
dv +
ˆ
e
y
∂g
∂v
dv +
ˆ
e
z
∂h
∂v
dv.
The cross product of these two displacements is the element of area of the
surface:
da = d
l
1
× d
l
2
=det
⎛
⎜
⎜
⎜
⎜
⎝
ˆ
e
x
ˆ
e
y
ˆ
e
z
∂f
∂u
∂g
∂u
∂h
∂u
∂f
∂v
∂g
∂v
∂h
∂v
⎞
⎟
⎟
⎟
⎟
⎠
dudv ≡ det
⎛
⎜
⎜
⎜
⎜
⎝
ˆ
e
x
ˆ
e
y
ˆ
e
z
∂x
∂u
∂y
∂u
∂z
∂u
∂x
∂v
∂y
∂v
∂z
∂v
⎞
⎟
⎟
⎟
⎟
⎠
dudv.
Using this in (13.3) we get
φ =
##
R
det
⎛
⎜
⎜
⎜
⎜
⎝
A
x
A
y
A
z
∂x
∂u
∂y
∂u
∂z
∂u
∂x
∂v
∂y
∂v
∂z
∂v
⎞
⎟
⎟
⎟
⎟
⎠
du dv, (13.5)
where A
x
, A
y
,andA
z
are considered functions of u and v obtained by substi-
tuting (13.4) for their arguments. Equation (13.5) is an integral over a region
R in the uv-plane determined by the range of the variables u and v sufficient
to describe the surface S.
The special, but important case, of a surface given by z = f(x, y) deserves
special attention. In this case the parametrization is
x = u, , y = v, z = f(u, v)
13.2 Flux Density = Divergence 371
and (13.5) yields
φ =
##
R
det
⎛
⎜
⎜
⎜
⎜
⎝
A
x
A
y
A
z
10
∂z
∂u
01
∂z
∂v
,
⎞
⎟
⎟
⎟
⎟
⎠
du dv
or, writing (x, y)for(u, v)
φ =
##
R
−A
x
∂z
∂x
− A
y
∂z
∂y
+ A
z
dx dy, (13.6)
where R is the projection of the surface S onto the xy-plane.
13.2 Flux Density = Divergence
The connection between flux and the strength of the source of a vector field
was mentioned above. We now analyze this connection further. The variation
in the strength of the source of a vector field is measured by the density of
the source. For example, the variation in the strength—concentration—of
the source of electrostatic (gravitational) field is measured by charge (mass)
density. We expect this variation to influence the intensity of flux at various
points in space.
13.2.1 Flux Density
Densities are physical quantities treated locally. A local consideration of flux,
therefore, requires the introduction of the notion of flux density:
notion of flux
density and
divergence of a
vector field
introduced
Box 13.2.1. Take a small volume around a point P , evaluate the total flux
of a vector field through the bounding surface of the volume, and divide
the result by the volume to get the flux density or divergence of the
vector field at P .
We denote the flux density by ρ
φ
for the moment. Later we shall introduce
another notation which is more commonly used.
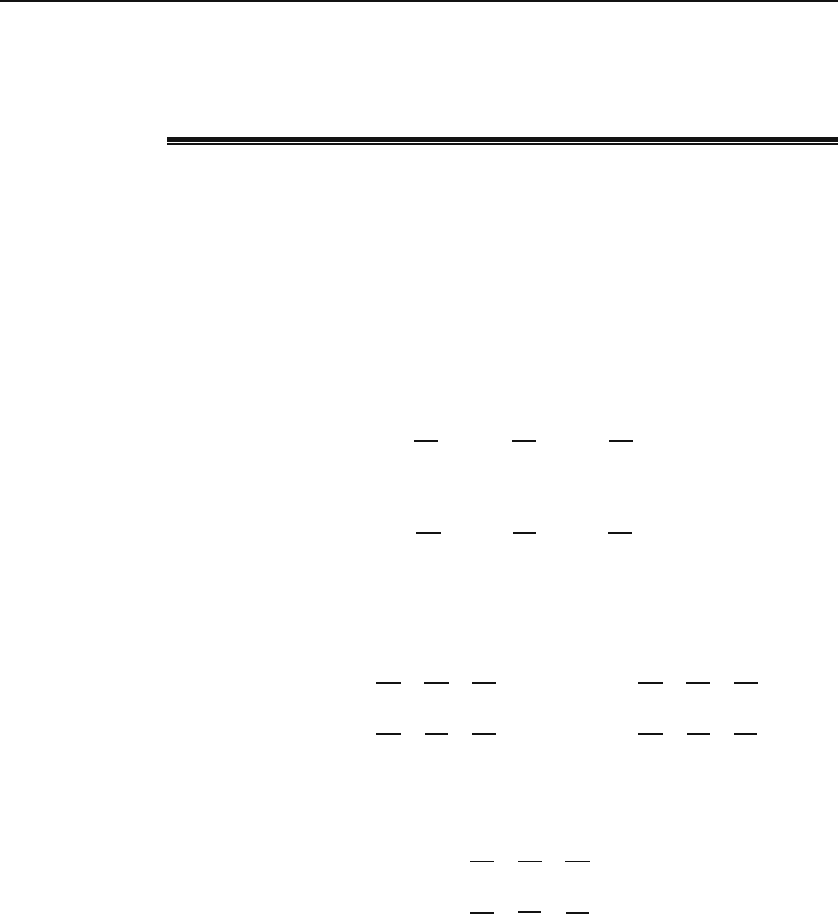
Let us quantify the discussion above for a vector field A. Consider a small
rectangular
6
volume ΔV centered at P with coordinates (x, y, z). Let the
sides of the box be Δx, Δy,andΔz as in Figure 13.4. We are interested in
6
The rectangular shape of the volume is not a restriction because it will be made smaller
and smaller at the end. In such a limit, any volume can be built from—a large number of—
these small rectangular boxes. Compare this with the rectangular strips used in calculating
the area under a curve.
372 Flux and Divergence
ˆ
e
z
A
z
ˆ
e
y
A
y
ˆ
e
x
A
x
(
x
,
y
,
z
)
Δ
x
Δ
y
Δ
z
A
Figure 13.4: The flux of the vector field A through a closed infinitesimal rectangular
surface.
the net outward
7
flux of the vector field, A(x, y, z). The six faces of the box
are assumed to be so small that the angle between the normal to each face
and the vector field A is constant over the area of the face. Since we are
calculating the outward flux, we must assume that
ˆ
e
n
is always pointing out
of the volume.
The total flux Δφ through the surface can be written as
Δφ =(Δφ
1
+Δφ
2
)+(Δφ
3
+Δφ
4
)+(Δφ
5
+Δφ
6
),
where each pair of parentheses indicates one coordinate axis. For instance,
Δφ
1
is the flux through the face having a normal component along the positive
x-axis, Δφ
2
is the flux through the face having a normal component along the
negative x-axis,andsoon.LetusfirstlookatΔφ
1
, which can be written as
Δφ
1
= A
1
·
ˆ
e
n
1
Δa
1
or, since
ˆ
e
n
1
is the same as
ˆ
e
x
,
Δφ
1
= A
1
·
ˆ
e
x
Δa
1
= A
1x
Δa
1
.
This requires some explanation. The subscript 1 in A
1x
indicates the evalu-
ation of the vector field at the midpoint
8
of the first face. The subscript x
in A
1x
, of course, means the x-component. So, A
1x
means the x-component
of A evaluated at the midpoint of the first face; Δa
1
istheareaofface1
which is simply ΔyΔz (see Figure 13.4). The center of the box—point P —
has coordinates (x, y, z) by assumption. Thus, the midpoint of face 1 will
have coordinates (x +Δx/2,y,z). Therefore,
Δφ
1
= A
x
x +
Δx
2
,y,z
ΔyΔz. (13.7)
7
The choice of outward direction is dictated by Box 12.1.3.
8
The restriction to midpoint is only for convenience. Since the area is small, any other
point of the face can be used.
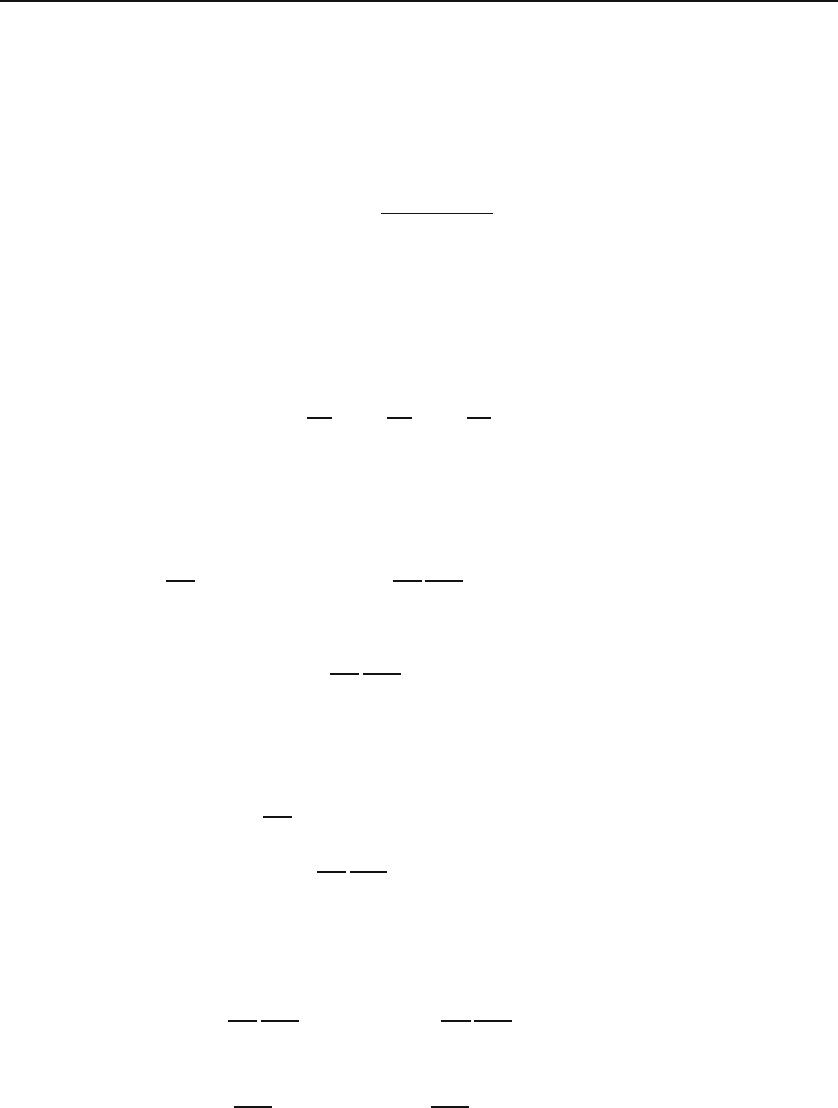
13.2 Flux Density = Divergence 373
The flux density that we are evaluating will be the density at P .Thus,
as a function of the three coordinates, the result will have to be given at the
coordinates of P ,namelyat(x, y, z). This means that in Equation (13.7),
all quantities must have (x, y, z) as their arguments. This suggests expanding
the function on the RHS of Equation (13.7) as a Taylor series about the point
(x, y, z). Recall from Chapter 10 that
f(x +Δx, y +Δy, z +Δz)=
∞
n=0
i+j+k=n
∂
n
ijk
f(x, y, z)
i!j!k!
(Δx)
i
(Δy)
j
(Δz)
k
.
We are interested only in the first power because the size of the box will
eventually tend to zero. Therefore, we write this in the following abbreviated
form:
f(x +Δx, y +Δy, z +Δz)
= f(x, y, z)+Δx
∂f
∂x
+Δy
∂f
∂y
+Δz
∂f
∂z
+ ··· , (13.8)
where it is understood that all derivatives are evaluated at (x, y, z). Applying
this result to the function on the RHS of Equation (13.7), for which Δy and
Δz are zero, yields
A
x
x +
Δx
2
,y,z
= A
x
(x, y, z)+
Δx
2
∂A
x
∂x
+0+0+···
and
Δφ
1
=
(
A
x
(x, y, z)+
Δx
2
∂A
x
∂x
)
ΔyΔz + ··· .
Similarly, for the second face we obtain
Δφ
2
= A
2
·
ˆ
e
n
2
Δa
2
= A
2
· (−
ˆ
e
x
)Δa
2
= −A
2x
ΔyΔz
= −A
x
x −
Δx
2
,y,z
ΔyΔz
= −
(
A
x
(x, y, z) −
Δx
2
∂A
x
∂x
+ ···
)
ΔyΔz.
Adding the expressions for Δφ
1
and Δφ
2
,weobtain
Δφ
1
+Δφ
2
=
(
A
x
(x, y, z)+
Δx
2
∂A
x
∂x
− A
x
(x, y, z)+
Δx
2
∂A
x
∂x
+ ···
)
ΔyΔz
or
Δφ
1
+Δφ
2
=
∂A
x
∂x
ΔxΔyΔz + ···=
∂A
x
∂x
ΔV + ··· .

374 Flux and Divergence
The reader may check that
Δφ
3
+Δφ
4
=
∂A
y
∂y
ΔV + ··· ,
Δφ
5
+Δφ
6
=
∂A
z
∂z
ΔV + ··· , (13.9)
so that the total flux through the small box is
Δφ =
∂A
x
∂x
+
∂A
y
∂y
+
∂A
z
∂z
ΔV + ··· .
The flux density, or divergence as it is more often called, can now be obtained
by dividing both sides by ΔV and taking the limit as ΔV → 0. Since all the
terms represented by dots are of at least the fourth order, they vanish in the
limit and we obtain
Theorem 13.2.1. The relation between the flux density of a vector field and
the derivatives of its components is
ρ
φ
≡ div A ≡ ∇ ·A = lim
ΔV →0
Δφ
ΔV
=
∂A
x
∂x
+
∂A
y
∂y
+
∂A
z
∂z
.
The term “divergence,” whose abbreviation is used as a symbol of flux
origin of the term
“divergence”
density, is reminiscent of water flowing away from its source, a fountain. In
this context, the flux density measures how quickly or intensely water “di-
verges” away from the fountain. The third notation ∇ · A combines the
dot product in terms of components with the definition of ∇ as given in
Equation (12.28).
9
13.2.2 Divergence Theorem
The use of the word (volume) density for divergence suggests that the total
flux through a (large) surface should be the (volume) integral of divergence.
However, any calculation of flux—even locally—requires a surface, as we saw
in the derivation of flux density. What are the “small” surfaces used in the
calculation of flux density, and how is the large surface related to them? The
answer to this question will come out of a treatment of an important theorem
in vector calculus which we investigate now.
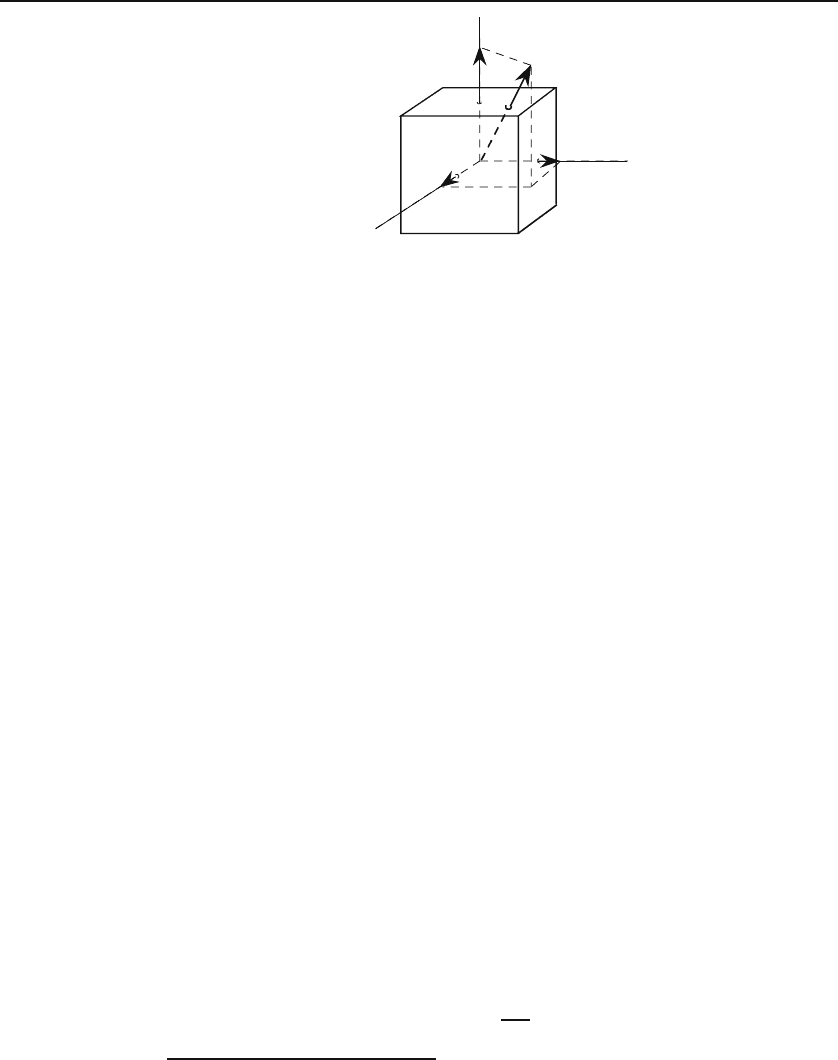
First consider two boxes with one face in common (Figure 13.5) and index
quantities related to the volume on the left by a andthoserelatedtotheone
on the right by b. The total flux is, of course, the sum of the fluxes through
all six faces of the composite box :
Δφ =(Δφ
1
+Δφ
2
)+(Δφ
3
+Δφ
4
)+(Δφ
5
+Δφ
6
),
9
This notation is misleading because, as we shall see later, in non-Cartesian coordinate
systems, the expression of divergence in terms of derivatives will not be equal to simply
the dot product of ∇ with the vector field. One should really think of ∇· A as a symbol,
equivalent to ρ
φ
or div A and not as an operation involving two vectors.

13.2 Flux Density = Divergence 375
(x
a
, y
a
, z
a
)
y
x
z
(x
b
, y
b
, z
b
)
Figure 13.5: The common boundaries contribute no net flux.
where, as before, Δφ
1
is the total flux through the face having a normal in
the positive x-direction, and Δφ
2
that through the face having a normal in
the negative x-direction, and so on. It is evident from Figure 13.5 that
Δφ
1
=Δφ
a
1
+Δφ
b
1
,
where Δφ
a
1
is the flux through the positive x face of box a and Δφ
b
1
is the
flux through the positive x face of box b. Using a similar notation, we can
write
Δφ
2
=Δφ
a
2
+Δφ
b
2
,
Δφ
5
+Δφ
6
=Δφ
a
5
+Δφ
b
5
+Δφ
a
6
+Δφ
b
6
.
However, for the y faces we have Δφ
3
=Δφ
b
3
and Δφ
4
=Δφ
a
4
, because the
face of the composite box in the positive y-direction belongs to box b and that
in the negative y-direction to box a. Now note that the outward flux through
the left face of box b is the negative of the outward flux through the right face
of box a;thatis,
Δφ
b
4
= −Δφ
a
3
⇒ Δφ
b
4
+Δφ
a
3
=0.
Thus, we obtain
Δφ
3
+Δφ
4
=Δφ
b
3
+Δφ
a
4
=Δφ
a
3
+Δφ
b
3
+Δφ
a
4
+Δφ
b
4
.
Using all the above relations yields
Δφ =(Δφ
a
1
+Δφ
a
2
)+(Δφ
a
3
+Δφ
a
4
)+(Δφ
a
5
+Δφ
a
6
)
+(Δφ
b
1
+Δφ
b
2
)+(Δφ
b
3
+Δφ
b
4
)+(Δφ
b
5
+Δφ
b
6
)
or Δφ =Δφ
a
+Δφ
b
,orΔφ =(∇·A)
a
ΔV
a
+(∇·A)
b
ΔV
b
. These equations
say that
Box 13.2.2. The total flux through the outer surface of a composite box
consisting of two adjacent boxes is equal to the sum of the total fluxes
through the bounding surfaces of the two boxes, including the common
boundary. Stated differently, in summing the total outward flux of adjacent
boxes, the contributions of the common boundary cancel.

376 Flux and Divergence
It is now clear how to generalize to a large surface bounding a volume: Di-
vide up the volume into N rectangular boxes and write φ ≈
N
i=1
(∇·A)
i
ΔV
i
.
The LHS of this equation is the outward flux through the bounding surface
only. Contributions from the sides of all inner boxes cancel out because
each face of a typical inner box is shared by another box whose outward
flux through that face is the negative of the outward flux of the original box.
However, boxes at the boundary cannot find enough boxes to cancel all their
flux contributions, leaving precisely the flux through the original surface. The
use of the approximation sign here reflects the fact that N, although large, is
not infinite, and that the boxes are not small enough. To attain equality we
must make the boxes smaller and smaller and their number larger and larger,
in which case we approach the integral:
φ =
##
V
#
∇ · A dV. (13.10)
Then, using Equation (13.2), we can state the important
the very
important
divergence
theorem
Theorem 13.2.2. (Divergence Theorem). The surface integral (flux) of
any vector field A through a closed surface S bounding a volume V is equal
to the volume integral of the divergence (or flux density) of A:
##
S
A ·da =
##
V
#
∇ · A dV. (13.11)
Let A = cf where c is an arbitrary constant vector and f a function.
Applying the divergence theorem to this A and using the readily verifiable
identity ∇ · (cf )=c ·∇f,weget
##
S
fc·da =
##
V
#
c·(∇f)dV or c·
⎛
⎝
##
S
fda
⎞
⎠
= c·
⎛
⎝
##
V
#
(∇f)dV
⎞
⎠
Since this holds for any c,wemusthave
##
S
fda =
##
V
#
∇fdV (13.12)
Example 13.2.3.
In this example we derive Gauss’s law for fields which vary
as the inverse of distance squared, specifically, gravitational and electrostatic fields.
Let Q be a source point (a point charge or a point mass) located at P
0
with position
vector r
0
and S a closed surface bounding a volume V .LetA(r) denote the field
produced by Q at the field point P with position vector r as shown in Figure 13.6(a).
We know that
A(r)=
KQ
|r − r
0
|
3
(r − r
0
). (13.13)
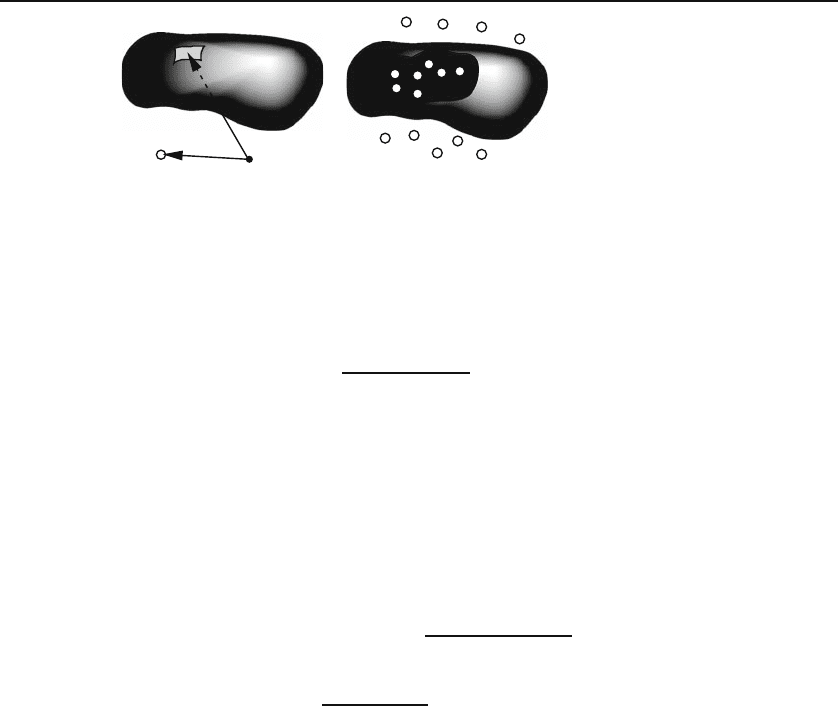
13.2 Flux Density = Divergence 377
S
O
P
0
r
r
0
(a)
(b)
Figure 13.6: Derivation of Gauss’s law for (a) a single point source, and (b) a number
of point sources.
The flux of A through S can be written immediately:
##
S
A · da =
##
S
KQ(r −r
0
) · da
|r − r
0
|
3
.
But the RHS is—apart from a constant—the solid angle subtended by S about P
0
.
Using Equation (12.7), we have
##
S
A · da =
0
4πKQ if P
0
is in V,
0ifP
0
is not in V.
(13.14)
If there are N point sources Q
1
,Q
2
,...,Q
N
,thenA will be the sum of individual
contributions, and we have
##
S
A · da =
##
S
N
k=1
A
k
· da =
N
k=1
##
S
KQ
k
(r
k
− r
0
) · da
|r
k
− r
0
|
3
= K
N
k=1
Q
k
##
S
(r
k
− r
0
) · da
|r
k
− r
0
|
3
= K
N
k=1
Q
k
Ω
k
,
where Ω
k
is zero if Q
k
is outside V ,and4π if it is inside [see Figure 13.6(b)]. Thus,
only the sources enclosed in the volume will contribute to the sum and we have
##
S
A · da =4πKQ
enc
, (13.15)
where Q
enc
is the amount of source enclosed in S.
global (integral)
form of Gauss’s
law
For electrostatics, K = k
e
=1/4π
0
, Q = q,andA = E,sothat
##
S
E · da = q
enc
/
0
. (13.16)
For gravitation, K = −G, Q = M,andA = g,sothat
##
S
g · da = −4πGM
enc
. (13.17)

378 Flux and Divergence
The minus sign appears in the gravitational case because of the permanent attraction
of gravity. Gauss’s law is very useful in calculating the fields of very symmetric source
distributions, and it is put to good use in introductory electromagnetic discussions.
The derivation above shows that it is just as useful in gravitational calculations.
Equation (13.15) is the integral or global form of Gauss’s law. We can also
derive the differential or local form of Gauss’s law by invoking the divergence
theorem and assigning a volume density ρ
Q
to Q
enc
:
LHS =
##
V
#
∇ · A dV, RHS = 4πK
##
V
#
ρ
Q
dV.
Since these relations are true for arbitrary V ,weobtain
local (differential)
form of Gauss’s
law
Theorem 13.2.4. (Differential Form of Gauss’s Law).Ifapointsource
produces a vector field A that obeys Equation (13.13), then for any volume
distribution ρ
Q
of the source we have ∇ · A =4πKρ
Q
.
This can easily be specialized to the two cases of interest, electrostatics
and gravity.
13.2.3 Continuity Equation
To improve our physical intuition of divergence, let us consider the flow of a
fluid of density ρ(x, y, z, t)andvelocityv(x, y, z, t). The arguments to follow
are more general. They can be applied to the flow (bulk motion) of many
physical quantities such as charge, mass, energy, momentum, etc. All that
needs to be done is to replace ρ—which is the mass density for the fluid
flow—with the density of the physical quantity.
We are interested in the amount of matter crossing a surface area Δa
per unit time. We denote this quantity momentarily by ΔM, and because
of its importance and wide use in various areas of physics, we shall derive
it in some detail. Take a small volume ΔV of the fluid in the shape of a
slanted cylinder. The lateral side of this volume is chosen to be instantaneously
in the same direction as the velocity v of the particles in the volume. For
large volumes this may not be possible, because the macroscopic motion of
particles is, in general, not smooth, with different parts having completely
different velocities. However, if the volume ΔV (as well as the time interval
of observation) is taken small enough, the variation in the velocity of the
enclosed particles will be negligible. This situation is shown in Figure 13.7.
The lateral length of the cylinder is vΔt where Δt is the time it takes the
particles inside to go from the base to the top, so that all particles inside will
have crossed the top of the cylinder in this time interval. Thus, we have
amount crossing top = amount in ΔV = ρΔV.
But ΔV =(vΔt) · Δa = v · Δa Δt, where the dot product has been used
because the base and the top are not perpendicular to the lateral surface.
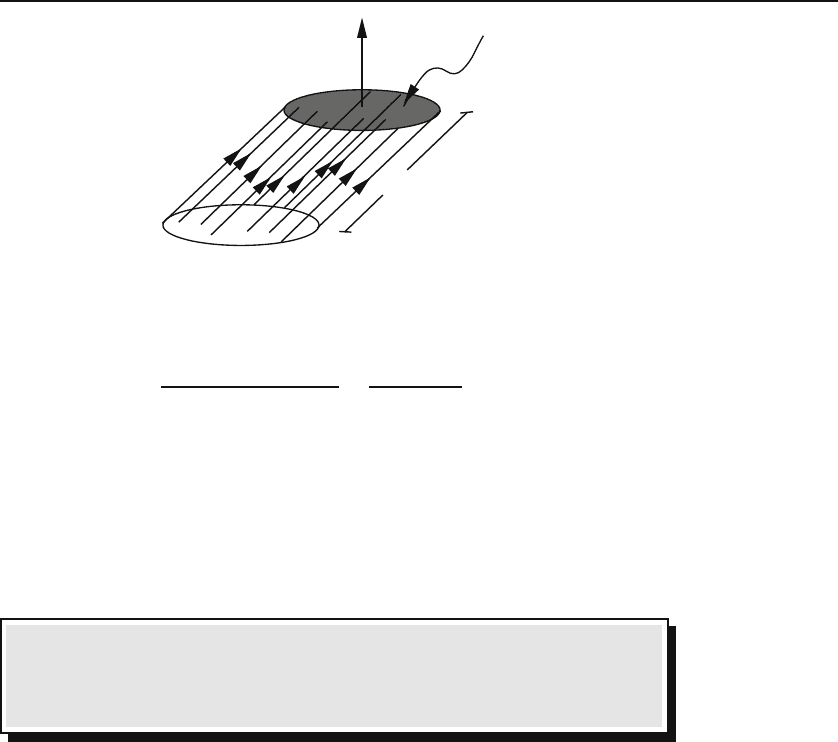
13.2 Flux Density = Divergence 379
vΔt
n
e
^
Δa
Figure 13.7: The flux through a small area is related to the current density.
Therefore,
ΔM =
amount crossing top
Δt
=
ρv · Δa Δt
Δt
=(ρv) · Δa.
The RHS of this equation is the flux of the vector field ρv which is called the
current density
mass current density, and usually denoted as J.
As indicated earlier, this result is general and applies to any physical
quantity in motion. We can therefore rewrite the equation in its most general
form as
Δφ
Q
=(ρ
Q
v) · Δa ≡ J
Q
·Δa. (13.18)
This is so important that we state it in words:
Box 13.2.3. The amount of a flowing physical quantity Q crossing an
area Δa per unit time is the flux J
Q
·Δa. The current density J
Q
at each
point is simply the product of volume density and velocity vector at that
point.
relation between
flux and current
density
For a (large) surface S we need to integrate the above relation:
φ
Q
=
##
S
(ρ
Q
v) · da ≡
##
S
J
Q
·da (13.19)
and if S is closed, the divergence theorem gives
φ
Q
=
##
S
J
Q
· da =
##
V
#
∇ · J
Q
dV. (13.20)
Let Q, which may change with time, denote the total amount of physical
quantity in the volume V . Then, clearly
Q(t)=
##
V
#
ρ
Q
dV =
##
V
#
ρ
Q
(r,t) dV (r),
