Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


122 Integration: Applications
Box 4.2.2. When gravitationally attracting objects outside it, a spherical mass
distribution acts as if all its mass were concentrated into a point at its center.
Newton spent approximately twenty years convincing himself of this result.
Because of the similarity between gravity and electrostatics, the conclusion above
can be applied to the electrostatic field as well. Thus, in particular, the electrostatic
field inside any uniformly charged shell is zero.
We take the final example of this section from mechanics and calculate the
moment of inertia of the foregoing shell about the polar axis. Recall that
moment of inertia
the moment of inertia of a mass distribution about an axis is defined as
I =
##
Ω
R
2
dm, (4.34)
where R is the distance from the integration point—location of dm—to the
reference axis.
Example 4.2.5.
The moment of inertia of the spherical shell segment is obtained
easily. All we need to note is that R = a sin θ
. Then Equation (4.34) gives
I =
##
Ω
(a sin θ
)
2
σa
2
sin θ
dθ
dϕ
= a
4
σ
#
α
0
sin
3
θ
dθ
#
2π
0
dϕ
=2πa
4
σ
1
3
cos
3
θ
− cos θ
!
α
0
=
2πa
4
σ
3
(cos
3
α − 3cosα +2).
We can express this in terms of total mass if we note that the area is given by
A =
##
Ω
a
2
sin θ
dθ
dϕ
=2πa
2
#
α
0
sin θ
dθ
=2πa
2
(1 − cos α)
so that
σ =
M
A
=
M
2πa
2
(1 − cos α)
.
Therefore,
I =
1
3
Ma
2
cos
3
α − 3cosα +2
1 − cos α
,
which reduces to I =
2
3
Ma
2
for a complete spherical shell (with α = π).
4.3 Applications: Triple Integrals
To illustrate the difficulty of calculations when appropriate coordinate systems
are not chosen, in the following example we calculate the gravitational field
of a uniform hemisphere at a point P on its axis in Cartesian coordinates.
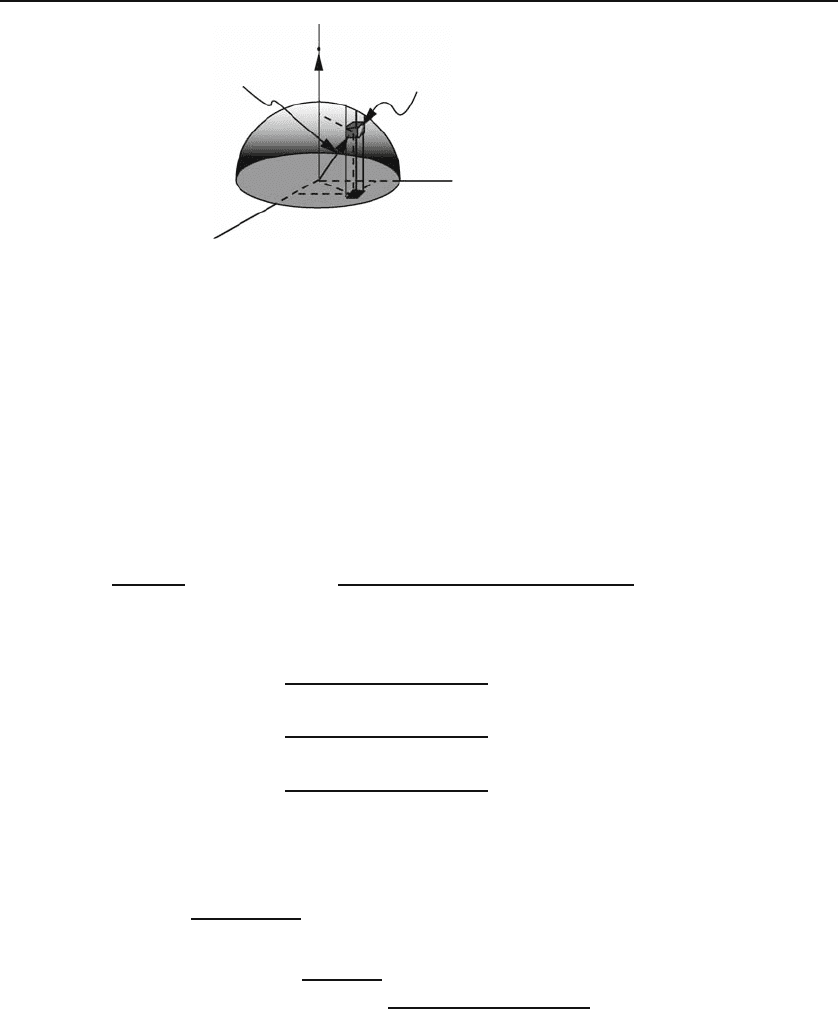
4.3 Applications: Triple Integrals 123
z
x
y
dV(r ) = dx dy dz
P
'
'
'
'
= (x , y , z )
'
'
'
r
'
r
Figure 4.13: Calculating the gravitational field of a hemisphere in the “unnatural”
Cartesian coordinates.
Example 4.3.1. The geometry of the problem is shown in Figure 4.13. The
location of P and the choice of axes indicate that
r = z
ˆ
e
z
, r
= x
ˆ
e
x
+ y
ˆ
e
y
+ z
ˆ
e
z
,
|r − r
|
3
=
,
x
2
+ y
2
+(z − z
)
2
-
3/2
,
dm(r
)=ρ
m
dV (r
)=ρ
m
dx
dy
dz
,
where ρ
m
is the uniform mass density. Thus,
g = −
##
Ω
Gdm(r
)
|r − r
|
3
(r − r
)=Gρ
m
##
Ω
dx
dy
dz
{x
ˆ
e
x
+ y
ˆ
e
y
+(z
− z)
ˆ
e
z
}
{x
2
+ y
2
+(z − z
)
2
}
3/2
with components
g
x
= Gρ
m
##
Ω
x
dx
dy
dz
{x
2
+ y
2
+(z − z
)
2
}
3/2
,
g
y
= Gρ
m
##
Ω
y
dx
dy
dz
{x
2
+ y
2
+(z − z
)
2
}
3/2
,
g
z
= Gρ
m
##
Ω
(z
− z) dx
dy
dz
{x
2
+ y
2
+(z − z
)
2
}
3/2
.
The limits of integrals associated with Ω can be done as discussed in Section 3.3.
In Figure 4.13, we have chosen the first integral to be along the z-axis. Then the
lower limit will be the xy-plane, or z
= 0, and the upper limit, the surface of
the hemisphere. A general point P
in Ω with coordinates (x
,y
,z
)willhitthe
hemisphere at z
=
a
2
− x
2
− y
2
. So, this will be the upper limit of the z
integration. Concentrating on the x-component for a moment, we thus write
g
x
= Gρ
m
##
S
x
dx
dy
#
√
a
2
−x
2
−y
2
0
dz
{x
2
+ y
2
+(z − z
)
2
}
3/2
,
where S is the projection of the hemispherical surface on the xy-plane. To do
the remaining integrations, we refer to Figure 4.14, where the projections of the
hemisphere and the point P
are shown. It is clear that the y
integration has
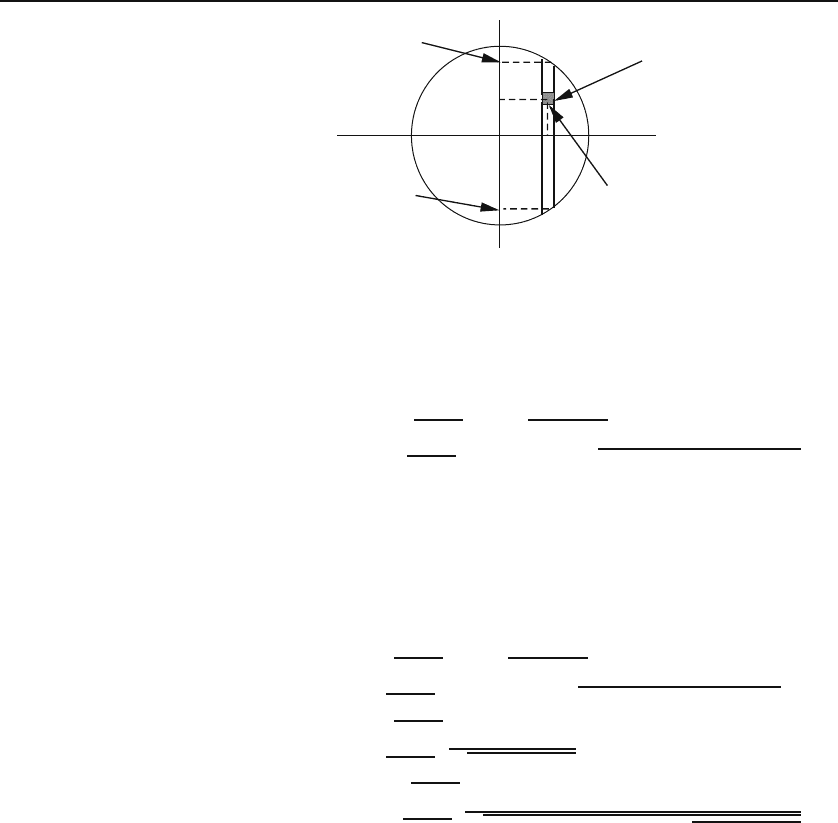
124 Integration: Applications
x
y
−a
+a
dx
y
x
y
lower
y
upper
dy
'
'
'
'
'
'
Figure 4.14: The projection of Ω, a hemisphere, in the xy-plane.
the lower semicircle as the lower limit and the upper semicircle as the upper limit.
Finally the x
integration has lower and upper limits of −a and +a, respectively.
We, therefore, have
g
x
= Gρ
m
#
+a
−a
x
dx
#
+
√
a
2
−x
2
−
√
a
2
−x
2
dy
#
√
a
2
−x
2
−y
2
0
dz
{x
2
+ y
2
+(z − z
)
2
}
3/2
.
Instead of looking up the integrals in an integral table, we note that the integrand
of the x
integration is an odd function. This is because it is the product of x
,which
is odd, and another function, in the form of a double integral whose integrand and
limits are even functions of x
. Since the interval of integration is symmetric, the
x
integration vanishes. A similar argument shows that the y
integration vanishes
as well. This is as expected intuitively: We expect the field to be along the z-axis.
Therefore, g
x
=0,g
y
=0,and
g
z
= Gρ
m
#
+a
−a
dx
#
+
√
a
2
−x
2
−
√
a
2
−x
2
dy
#
√
a
2
−x
2
−y
2
0
(z
− z) dz
{x
2
+ y
2
+(z − z
)
2
}
3/2
= Gρ
m
#
+a
−a
dx
#
+
√
a
2
−x
2
−
√
a
2
−x
2
dy
x
2
+ y
2
+ z
2
− Gρ
m
#
+a
−a
dx
#
+
√
a
2
−x
2
−
√
a
2
−x
2
dy
a
2
+ z
2
+ x
2
+ y
2
− 2z
a
2
− x
2
− y
2
.
The y
integration in the first integral can be done, but the remaining x
integration
will be complicated. The second y
integral cannot even be performed in closed form.
This difficulty is a result of our poor choice of coordinates whereby the boundary of
the region of integration does not turn out to be a “natural” surface.
The example of the hemisphere in Cartesian coordinates indicates the
difficulty encountered when the boundaries of the integration region do not
match the primary surfaces of the coordinate system. In the next example,
we calculate the gravitational field of the hemisphere in spherical coordinates.
Example 4.3.2.
The spherical coordinate system makes the problem so man-
ageable that we can consider a more general mass distribution. We will calculate
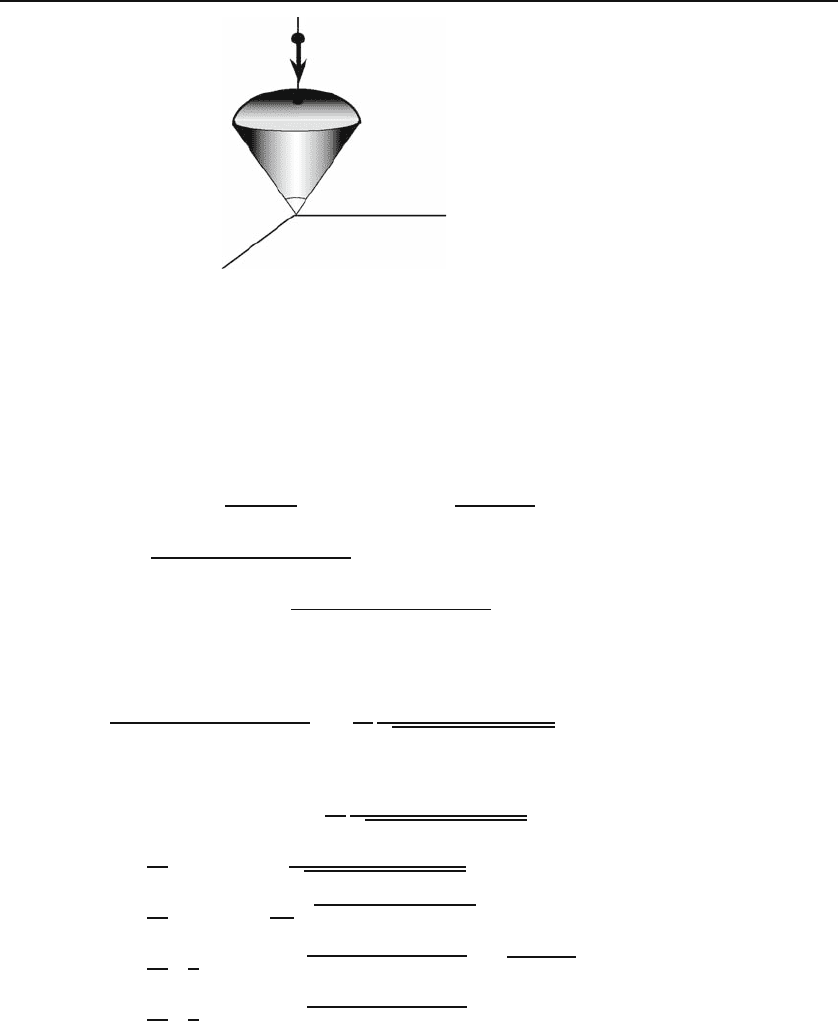
4.3 Applications: Triple Integrals 125
P
g
2α
Figure 4.15: The gravitational field of a solid cone with a spherically curved top.
the gravitational field of a cone-shaped segment of a solid sphere of half-angle α as
shown in Figure 4.15. We are interested in the field at a point P on the axis of the
cone as shown. Since
ˆ
e
θ
and
ˆ
e
ϕ
cannot be defined at P (why?), we expect, from
physical intuition, that the only surviving component of the gravitational field is
radial. This component is obtained by dotting the vector field with
ˆ
e
r
:
g
r
=
ˆ
e
r
· g =
ˆ
e
r
·
(
−
##
Ω
Gdm(r
)
|r − r
|
3
(r − r
)
)
= −G
##
Ω
dm(r
)
|r − r
|
3/2
(r − r
cos θ
)
= −Gρ
m
##
Ω
r
2
sin θ
dr
dθ
dϕ
(r
2
+ r
2
− 2rr
cos θ
)
3/2
(r −r
cos θ
)
= −Gρ
m
#
2π
0
dϕ
#
a
0
r
2
dr
#
α
0
sin θ
dθ
(r
2
+ r
2
− 2rr
cos θ
)
3/2
(r −r
cos θ
).
To do the integrations, we use the technique of differentiating inside the integral
and note that
r −r
cos θ
(r
2
+ r
2
− 2rr
cos θ
)
3/2
= −
∂
∂r
1
√
r
2
+ r
2
− 2rr
cos θ
.
Therefore, the integral becomes
g
r
=2πGρ
m
#
a
0
r
2
dr
#
α
0
sin θ
dθ
∂
∂r
1
√
r
2
+ r
2
− 2rr
cos θ
=2πGρ
m
∂
∂r
#
a
0
r
2
dr
#
α
0
sin θ
dθ
√
r
2
+ r
2
− 2rr
cos θ
=2πGρ
m
∂
∂r
#
a
0
r
2
dr
1
rr
r
2
+ r
2
− 2rr
cos θ
α
0
=2πGρ
m
∂
∂r
(
1
r
#
a
0
r
dr
r
2
+ r
2
− 2rr
cos α −
(r − r
)
2
)
=2πGρ
m
∂
∂r
(
1
r
#
a
0
r
dr
r
2
+ r
2
− 2rr
cos α −|r − r
|
)
. (4.35)
The integral involving the absolute value can be done easily. However, we have
to be careful about the relative size of r, a,andr
. We therefore consider two cases:
r ≥ a and r ≤ a. Keeping in mind that r
≤ a, the first case yields
126 Integration: Applications
#
a
0
r
|r −r
|dr
=
#
a
0
r
(r −r
) dr
=
ra
2
2
−
a
3
3
,r≥ a.
For the second case, we have to split the interval of integration in two, and write
the absolute value accordingly:
#
a
0
r
|r −r
|dr
=
#
r
0
r
(r −r
) dr
+
#
a
r
r
(r
− r) dr
=
r
3
3
+
a
3
3
−
ra
2
2
,r≤ a.
Substituting these in Equation (4.35), we get
g
r
=2πGρ
m
∂
∂r
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
a
3
3r
−
a
2
2
+
1
r
#
a
0
r
√
r
2
+ r
2
− 2rr
cos αdr
if r ≥ a,
a
2
2
−
r
2
3
−
a
3
3r
+
1
r
#
a
0
r
√
r
2
+ r
2
− 2rr
cos αdr
if r ≤ a.
The remaining integral can also be performed with the result
1
r
#
a
0
r
r
2
+ r
2
− 2rr
cos αdr
= −
r
2
12
(1 − 3cos2α)
+
r
2
+ a
2
− 2ra cos α
a
2
3r
+
r
12
−
a cos α
6
−
r cos 2α
4
+
r
2
cos α sin
2
α
2
ln
a − r cos α +
√
r
2
+ a
2
− 2ra cos α
r − r cos α
.
The special case of α = π, i.e., a full sphere, is very important, because his-
torically it motivated the rapid development of integral calculus. For this case, we
have
1
r
#
a
0
r
r
2
+ r
2
− 2rr
cos αdr
α=π
−→
r
2
6
+(a + r)
a
2
3r
−
r
6
+
a
6
,
whereby the radial component of the field becomes
g
r
=2πGρ
m
∂
∂r
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
a
3
3r
−
a
2
2
+
r
2
6
+(a + r)
a
2
3r
−
r
6
+
a
6
if r ≥ a,
a
2
2
−
r
2
6
−
a
3
3r
+(a + r)
a
2
3r
−
r
6
+
a
6
if r ≤ a,
=2πGρ
m
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
−
2a
3
3r
2
if r ≥ a
−
2r
3
if r ≤ a
=
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
−
GM
r
2
if r ≥ a,
−
4πGρ
m
r
3
if r ≤ a.
4.3 Applications: Triple Integrals 127
The first result is the well-known fact that the field outside a uniform sphere is the
same as the field of a point charge with the same mass concentrated at the center
of the original sphere. The second result, usually obtained in electrostatics by using
Gauss’s law, would not have been obtained if we had not used absolute values when
extracting a square root.
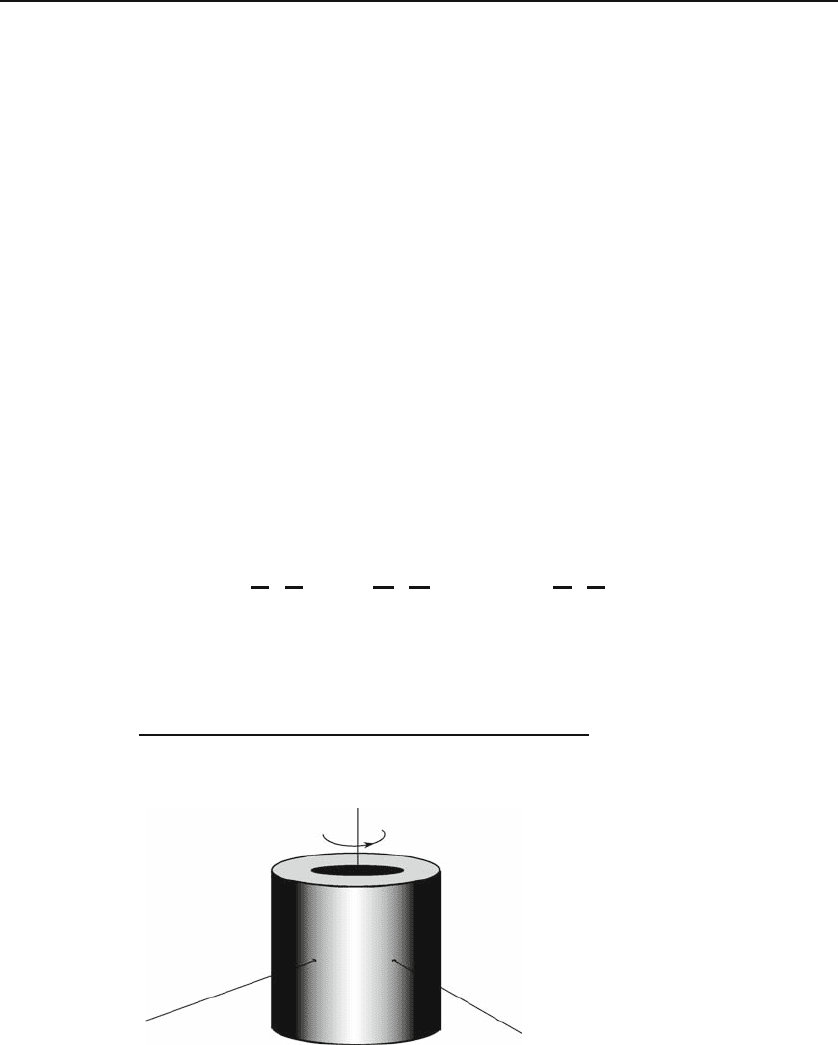
Example 4.3.3. A uniformly charged hollow cylinder of length L and volume
charge density ρ
q
has an inner radius a and an outer radius b (see Figure 4.16).
The cylinder is rotating with constant angular speed ω about its axis. We want
to find the magnetic field produced by this motion of charges. We note that the
problem has an azimuthal symmetry, so we do not lose generality if we choose our
coordinates so that our field point P lies in the xz-plane. This is equivalent to setting
ϕ =0.
We use cylindrical coordinates in Equation (4.17) to find the magnetic field. For
a general field point, we have
r = ρ
ˆ
e
ρ
+ z
ˆ
e
z
, r
= ρ
ˆ
e
ρ
+ z
ˆ
e
z
,
r − r
= ρ
ˆ
e
ρ
− ρ
ˆ
e
ρ
+(z − z
)
ˆ
e
z
,
|r − r
|
3
=
,
ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+(z − z
)
2
-
3/2
,
dq(r
)=ρ
q
dV (r
)=ρ
q
ρ
dρ
dϕ
dz
, v(r
)=ρ
ω
ˆ
e
ϕ
,
so that
v(r
) × (r − r
)=ωρρ
ˆ
e
ϕ
×
ˆ
e
ρ
−
ˆ
e
z
cos ϕ
−ωρ
2
ˆ
e
ϕ
×
ˆ
e
ρ
−
ˆ
e
z
+ωρ
(z −z
)
ˆ
e
ϕ
×
ˆ
e
z
ˆ
e
ρ
= ωρ
(z − z
)
ˆ
e
ρ
+ ω(ρ
2
− ρρ
cos ϕ
)
ˆ
e
z
.
Substituting all these results in Equation (4.17), we obtain
B =
##
Ω
ωk
m
(ρ
q
ρ
dρ
dϕ
dz
)
.
ρ
(z −z
)
ˆ
e
ρ
+(ρ
2
− ρρ
cos ϕ
)
ˆ
e
z
/
,
ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+(z − z
)
2
-
3/2
.
x
y
z
Figure 4.16: The charged rotating hollow cylinder produces a magnetic field due to
the motion of charges.

128 Integration: Applications
The cylindrical components are obtained by dotting this equation with the cylindri-
cal unit vectors at P :
B
ρ
= B ·
ˆ
e
ρ
= ωk
m
ρ
q
#
2π
0
#
b
a
#
L/2
−L/2
ρ
2
(z − z
)cosϕ
dρ
dϕ
dz
,
ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+(z − z
)
2
-
3/2
,
B
ϕ
= B ·
ˆ
e
ϕ
= ωk
m
ρ
q
#
2π
0
#
b
a
#
L/2
−L/2
ρ
2
(z −z
)sinϕ
dρ
dϕ
dz
,
ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+(z − z
)
2
-
3/2
=0,
B
z
= B ·
ˆ
e
z
= ωk
m
ρ
q
#
2π
0
#
b
a
#
L/2
−L/2
ρ
3
− ρρ
2
cos ϕ
!
dρ
dϕ
dz
,
ρ
2
+ ρ
2
− 2ρρ
cos ϕ
+(z − z
)
2
-
3/2
.
The middle equation gives zero as a result of the ϕ
integration. It turns out
that the z
and ρ
integrations of the remaining integrals can be performed in
closed form. However, the results are very complicated and will not be repro-
duced here. Furthermore, the ϕ
integration has no closed form and must be done
numerically.
We can also obtain the components of B in other coordinate systems by dotting
B into the corresponding unit vectors. The reader may check, for example, that in
Cartesian coordinates, B
x
= B ·
ˆ
e
x
isthesameasB
ρ
above and B
y
is the same
as B
ϕ
, i.e., B
y
= 0. This is due to the particular choice of our coordinate system
(ϕ =0).
4.4 Problems
4.1. Differentiate Equation (4.2) to find the velocity and acceleration and
compare with the expected results.
4.2. By choosing a coordinate system properly, write down the simplest para-
metric equation for the following curves. In each case specify the range of the
parameter you use:
(a) a rectangle of sides a and b,lyinginthexy-plane with center at the origin
and sides parallel to the axes;
(b) an ellipse with semi-major and semi-minor axes a and b;
(c) a helix wrapped around a cylinder with an elliptical cross section of the
type described in (b); and
(d) a helix wrapped around a cone.
4.3. Assume that the parametric equations of a linear charge density are
x
= f(t),y
= g(t),z
= h(t). By writing everything in Equation (4.3) in
Cartesian coordinates, show that
E =
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[g
(t)]
2
+[h
(t)]
2
3
[x − f(t)]
2
+[y − g(t)]
2
+[z − h(t)]
2
4
3/2
×
[x − f(t)]
ˆ
e
x
+[y − g(t)]
ˆ
e
y
+[z − h(t)]
ˆ
e
z
!
dt. (4.36)
4.4 Problems 129
and that
E
x
=
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[g
(t)]
2
+[h
(t)]
2
3
[x − f(t)]
2
+[y − g(t)]
2
+[z − h(t)]
2
4
3/2
[x − f(t)] dt
E
y
=
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[g
(t)]
2
+[h
(t)]
2
3
[x − f(t)]
2
+[y − g(t)]
2
+[z − h(t)]
2
4
3/2
[y − g(t)] dt (4.37)
E
z
=
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[g
(t)]
2
+[h
(t)]
2
3
[x − f(t)]
2
+[y − g(t)]
2
+[z − h(t)]
2
4
3/2
[z − h(t)] dt
and
Φ(x, y, z)=
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[g
(t)]
2
+[h
(t)]
2
3
[x − f(t)]
2
+[y − g(t)]
2
+[z − h(t)]
2
4
1/2
dt
How is Λ(t) related to λ(r
)?
4.4. (a) Show that
ˆ
e
ρ
·
ˆ
e
x
=
x
x
2
+ y
2
,
ˆ
e
ρ
·
ˆ
e
y
=
y
x
2
+ y
2
.
(b) Similarly, express
ˆ
e
ϕ
·
ˆ
e
x
and
ˆ
e
ϕ
·
ˆ
e
y
in Cartesian coordinates.
(c) Use (a), (b), and Equation (4.36) to find the general expressions for E
ρ
and
E
ϕ
as integrals in Cartesian coordinates similar to the integrals of Equation
(4.37).
4.5. (a) Find the nine dot products of all Cartesian and spherical unit vectors
and express the results in terms of Cartesian coordinates.
(b) Use (a) and Equation (4.36) to find general expressions for E
r
, E
θ
,and
E
ϕ
as integrals in Cartesian coordinates similar to the integrals of Equation
(4.37).
4.6. Assume that the parametric equations of a linear charge density are
ρ
= f (t),ϕ
= g(t),z
= h(t). By writing everything in Equation (4.3) in
cylindrical coordinates, show that Equation (4.11) holds and that
E
ρ
=
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[f(t)]
2
[g
(t)]
2
+[h
(t)]
2
3
ρ
2
+[f(t)]
2
− 2ρf(t)cos
ϕ −g(t)
!
+[z − h(t)]
2
4
3/2
×
.
ρ − f(t)cos
g(t) − ϕ
!/
dt (4.38)
E
ϕ
= −
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[f(t)]
2
[g
(t)]
2
+[h
(t)]
2
3
ρ
2
+[f(t)]
2
− 2ρf(t)cos
ϕ −g(t)
!
+[z − h(t)]
2
4
3/2
(4.39)
× f (t)sin
g(t) −ϕ
!
dt

130 Integration: Applications
E
z
=
#
b
a
k
e
Λ(t)
[f
(t)]
2
+[f(t)]
2
[g
(t)]
2
+[h
(t)]
2
3
ρ
2
+[f(t)]
2
− 2ρf(t)cos
ϕ −g(t)
!
+[z − h(t)]
2
4
3/2
(4.40)
×
.
z − h(t)
/
dt
and
Φ=
#
b
a
k
e
Λ(t)
[f
(t)]
2
+ f
2
(t)[g
(t)]
2
+[h
(t)]
2
3
ρ
2
+ f
2
(t) − 2ρf(t)cos
ϕ −g(t)
!
+[z − h(t)]
2
4
1/2
dt
How is Λ(t) related to λ(r
)?
4.7. Use (4.11) to calculate Cartesian and spherical components of the electric
field in terms of integrals in cylindrical variables similar to (4.38).
4.8. Use the cylindrical coordinates for the integration variables of Example
4.1.3, but calculate the Cartesian components of E.
4.9. A uniformly charged infinitely thin circular ring of radius a has total
charge Q. Place the ring in the xy-plane with its center at the origin. Use
cylindrical coordinates.
(a) Find the electrostatic potential at P with cylindrical coordinates (ρ, ϕ, z)
in terms of a single integral.
(b) Find the analytic form of the potential if P is on the z-axis (evaluate the
integral).
(c) Find the potential at a point in the xy-plane a distance 2a from the origin.
Give your answer as a number times k
e
Q/a.
4.10. Write a general formula for Φ(r) of a charged curve in spherical coor-
dinates.
4.11. A straight-line segment of length 2L is placed on the z-axis with its
midpoint at the origin. The segment has a linear charge density given by
λ(x, y, z)=
Q
|z| + a
,
where Q and a are constants with a>0. Find the electrostatic potential of
this charge distribution at a point on the x-axis in Cartesian coordinates.
4.12. Same as the previous problem, except that
λ(x, y, z)=
aQ
z
2
+ a
2
.
Look up the integral in an integral table.
(a) Does anything peculiar happen at x = ±a? Based on the integration
result? Based on physical intuition? Look at the result carefully and reconcile
any conflict.
(b) What is the potential when L →∞?

4.4 Problems 131
4.13. A segment of the parabola y = x
2
/a—with a a constant—extending
from x =0tox = L has a linear charge density given by
λ(x, y, z)=
λ
0
1+(2x/a)
2
,
where λ
0
is a constant. Find the potential and the electric field at the point
(0, 0,z). What are Φ and E at (0, 0,a/2)? Simplify your results as much as
possible.
4.14. A circular ring of radius a is uniformly charged with linear density λ.
(a) Find an expression for each of the three components of the electric field
at an arbitrary point in space in terms of an integral in an appropriate coor-
dinate system. Evaluate the integrals whenever possible.
(b) Find the components of the field at the point P showninFigure4.17.
Express your answers as a numerical multiple of k
e
λ/a.
(c) Find the electrostatic potential at the point P shown in Figure 4.17. Ex-
press your answer as a numerical multiple of k
e
λ.
For (b) and (c) you will need to evaluate certain integrals numerically.
4.15. Consider a uniform linear charge distribution in the form of an ellipse
with linear charge density λ. The semi-major and semi-minor axes of the el-
lipse are a and b, respectively. Use Cartesian coordinates and the parametric
equation of the ellipse.
(a) Write down the integrals that give the electric field and the electric po-
tential at an arbitrary point P in space.
(b) Specialize to the case where P lies on the axis that is perpendicular to the
plane of the ellipse and passes through its center.
(c) Specialize (a) to the case where P lies on the line containing the minor
axis.
4.16. Consider a uniform linear charge distribution in the form of an ellipse
with linear charge density λ locatedinthexy-plane. The semi-major and
semi-minor axes of the ellipse are 2a and a, respectively.
(a) Write the Cartesian parameterization of the ellipse in terms of trigono-
metric functions.
2a
a
P
Figure 4.17: The figure for Problems 4.14 and 4.21.
